Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
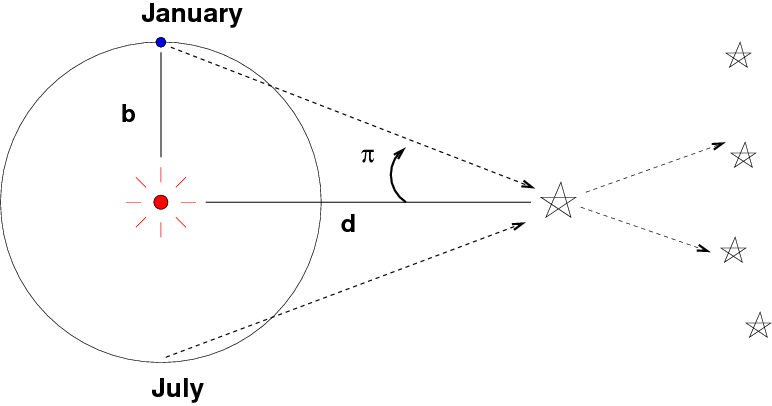
Parallax is the apparent shift in position of a nearby object when it is viewed from different locations. Those might be two different observatories on the Earth's surface (as was the case in the famous transits of Venus in the eighteenth and nineteenth centuries), but, in most astronomical applications, are two spots in Earth's orbit around the Sun:
If one knows the value of the baseline distance b, and can measure the parallax angle π
Yes, I know this is confusing. Yes, astronomers back in the old days should have picked a better letter. Sometimes you see the "curly pi" ϖ used to denote this angle, but few font families include it, so the parallax angle is usually written with the ordinary Greek letter π.
then one can use simple geometry to compute the distance to the target object d.
Q: Write a simple formula for d.
Of course, that simple formula ignores many complications. For example,
But one can work around these issues, or at least place constraints on their consequences.
The importance of parallax lies in its fundamental simplicity: we humans understand geometry, and trust it. As long as we can make measurements of the angular displacements over time, we can use the resulting distances with confidence.
There may be minor issues involving corrections for the small shifts of the background reference stars themselves; but if we choose to use galaxies or quasars as the reference sources, we can avoid those completely.
Most important of all, parallax is a direct method of measuring distances. It relies on a single assumed quantity: the astronomical unit (AU) = the distance from Earth to Sun. Back in the 1800s and early 1900s, this was indeed a major issue, and astronomers made great efforts to pin down the value of the AU. But these days, thanks to radar and spacecraft flying through the solar system, we do have a very, very good idea for the size of the AU. For example, the JPL Horizons system uses a value taken from the Planetary and Lunar Ephemerides DE430 and DE431, which list
1 AU = 149597870.700 km
That's ... quite a few signficant figures.
And that's it. Heliocentric parallax does NOT require any assumptions about stellar luminosity or evolution, or the distribution of sizes and colors of stars, or the spectral energy distribution of glowing hydrogen gas.
So, if astronomers can measure a distance via parallax, they will rely on it much more than distances determined by other methods.
In 2002, the asteroid 2002 NY40 flew past the Earth at a distance of less than one million kilometers. I used a telescope at the RIT Observatory in upstate New York to take its picture ...
... at exactly the same time that one of my colleagues at the Naval Academy in Annapolis, MD, did the same with her telescope:
If you compare the two images carefully, you should see that the background stars line up in the two images -- but the nearby asteroid clearly "jumps" from one image to the next due to parallax. (Click on the image below to blink the images).
We knew the distance between Rochester and Annapolis, and we could measure the size of the shift in the asteroid's position as seen from the two sites. With a little bit of geometry -- well, no, with quite a lot, actually -- we were able to calculate the distance to the asteroid.
It sounds as if using this technique to measure the distances to other stars should be pretty easy. In practice, though, it isn't quite so simple. There are a number of complications.
First, what exactly do we expect to see? As the Earth orbits the Sun, our point of view shifts back and forth, and so we ought to see nearby stars also shift back and forth, back and forth, relative to the distant ones. A simple, back-and-forth linear motion -- right?
Well, not quite. There's a complication due to the motion of our solar system and other stars in the Milky Way Galaxy. Even though most stars are circling the center of the Galaxy in the same general direction, each moves with a slightly different speed and direction. The result is that, over periods of decades and centuries and millenia, nearby stars appear to drift slowly across the sky. We call this proper motion.
The stars in the Big Dipper, which are relatively close to the Sun (only about 20-30 parsecs away), provide a dramatic illustration. Click on the picture below to watch a movie showing 200,000 years of proper motion.
Movie courtesy of
Tony Dunn's proper motion simulator -- thanks, Tony!
So, if we make careful measurements of the position of a nearby stars over a period of several years, we expect to see it move in a path which combines
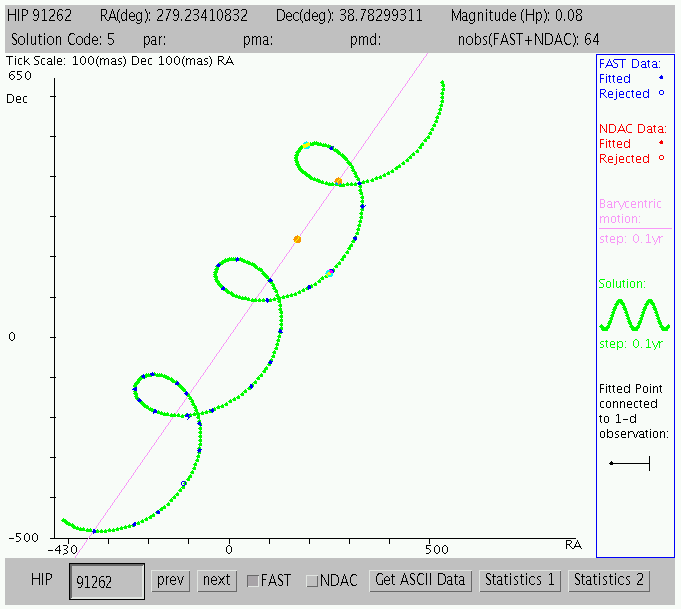
The result is something like a helix or corkscrew. You can see examples from the Hipparcos Intermediate Data archive by downloading and running their Java applet. The example below belongs to one of the brightest stars in the summer sky.
Thanks to the
European Space Agency
See also alternate version
You should be able to look at the diagram above and use the side-to-side shift to estimate the distance to this star. Can you do it?
Q: What is the amplitude of the side-to-side motion around
the diagonal straight line? The units on both
axes are milli-arcseconds.
Q: What is the amplitude of the parallax motion of this star,
expressed in arcseconds?
Q: What is the distance to this star, expressed in parsecs?
By the way, do you know which star this is? The figure above provides its Right Ascension and Declination. If you were to type those coordinates into
perhaps you could identify it.
This seems relatively straightforward: take pictures of a nearby star 20 or 40 times over the course of several years, measure its position relative to distant stars carefully, fit a model consisting of some linear motion plus an elliptical component, and *poof* out pops the star's distance. What's so hard about that?
Well, I've neglected just one thing in this discussion so far: scale. Just how large are these motions? And how precisely can we measure the position of a star from a typical image?
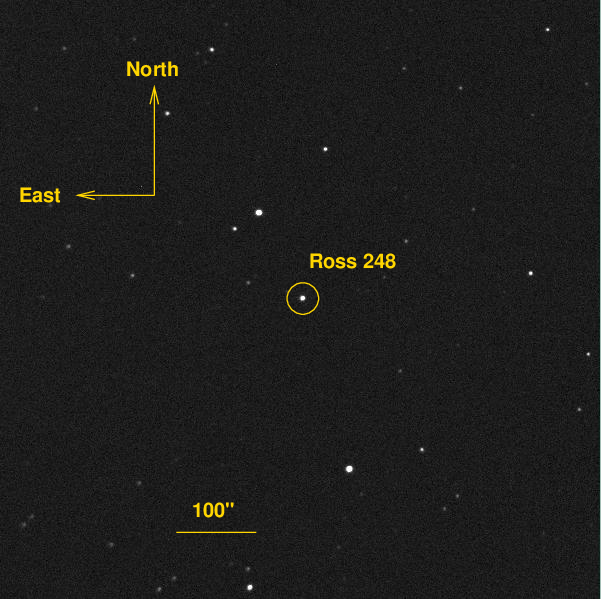
Consider the image below, which shows the nearby star Ross 248. This is one of many CCD images I have acquired of this star with the 12-inch telescope at the RIT Observatory.
The target has a proper motion to the South, so if we were to measure it over a three-year period, we ought to see it move in a pattern like this:
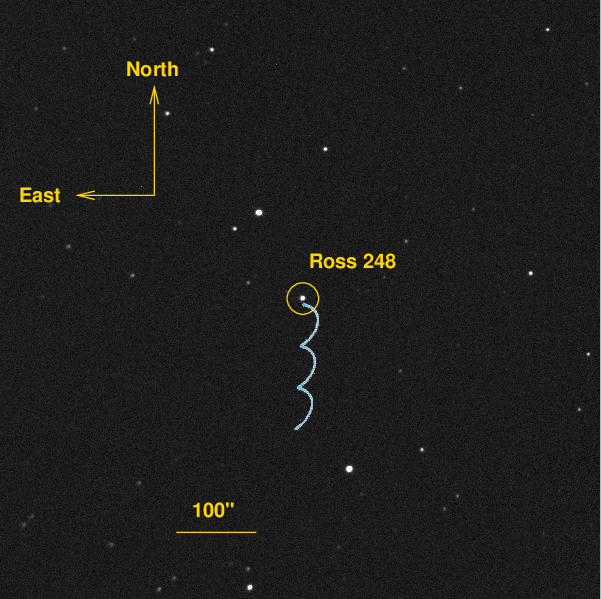
Simple, right? Measure the size of the "wiggles" in its motion, and use them to determine the parallax angle, and thence the distance to the star. Done!
There just one little complication. In the picture above, I've drawn the motion of Ross 248 in a slightly exaggerated way so that it's easier for you to see. The real motion is a bit smaller ...
Because the motion has a small amplitude, it's not quite so easy to measure accurately. Still, with some care, this is still not a big deal, right?
Nope, I'm lying. I still haven't drawn the motion at its proper size. Let's zoom in a bit more.
Okay, NOW I've drawn the motion of Ross 248 at its proper scale. Over this 3-year period, the star will move about 4.8 arcseconds to the South. Since the pixels on the camera at the RIT Observatory subtend 1.25 arcseconds each, this corresponds to a motion of about 3.8 pixels.
Oh, but wait -- it's not the long axis of this motion that we want to measure -- it's the short axis, running roughly East-West, representing the shift due to the Earth's motion around the Sun. What we really want to measure is THIS motion:
Of course, the full side-to-side motion is TWICE the parallax angle, so we really need to figure out half of that shift. As you can read elsewhere, in order to use parallax to determine the distance to a star accurately, one must measure the parallax angle with an uncertainty of at most ten percent. In the figure below, the red square illustrates the precision to which we must find that angle.
Oh, and one more thing: this particular example, Ross 248, is one of the closest stars to our solar system: the ninth-closest stellar system, in fact. A more typical parallax measurement requires precision which is 10 times, or even 100 times, higher than this.
NOW you may start to understand why measuring the distances to stars is not so easy ....
Of course, optical telescopes are not the only ones which can make parallax measurements. Any telescope on (or around) the Earth will share the annual journal, and so have a chance to measure the parallactic shifts of celestial sources.
Stars emit most of their energy in the optical region of the spectrum, and very little in the radio; it isn't possible to detect most stars with radio telescopes. Clouds of gas and dust do emit plenty of radio waves, but they are for the most part large, extended sources, not the compact objects one requires for parallax measurements.
However, there are some circumstances which do allow radio astronomers to apply the power of interferometry to make very precise measurements of the positions of compact radio sources, and therefore to determine the distances to those sources via parallax. The key element is the maser emission from small clumps of gas within some star-forming regions. Astronomical masers arise within compact volumes, thus appearing as point sources to our radio telescopes, and produce radiation of very pure frequency. This combination allows astronomers to determine their positions with very small uncertainties.
One example of parallax measurements in the radio regime is provided by the Japanese VERA project. VERA is a array of four radio dishes stretched out across the Japanese archipelago.
Image courtesy of
The VERA group and the National Astronomical Observatory of Japan
A very important point here is that, by combining the signals collected from several different radio dishes, we greatly decrease the effective size of the point-spread-function (PSF) of radio images; and those ultra-sharp images allow us to make ultra-precise measurements of the positions of unresolved features, such as the masers in this star-forming region.
Let's compare the sizes of the PSF of an optical telescope and the VERA radio interferometer, to see how much better we might be able to measure parallax. To a good approximation, the angular size of the PSF (in radians) depends only on the wavelength of light, λ, and the effective diameter of the telescope (or interferometer), D.
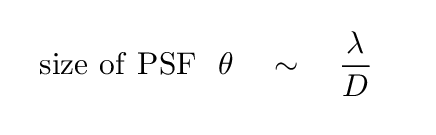
Q: What is the diffraction limit for an optical
telescope like Hipparcos, which had a mirror
of diameter d = 29 cm and measured light
of wavelength λ = 500 nm?
Q: What is the diffraction limit for a radio
interferometer like VERA, which has a typical
spacing of d = 1300 km and measures
radio waves from water masers at a frequency
of f = 22.2 GHz?
If one looks at star-forming regions, such as S269, with an optical telescope, one sees clumps of stars immersed in gas and dust. If one looks with a radio interferometer, one can see much finer details. Compare the scales on the IR picture at left with the VERA map at lower right.
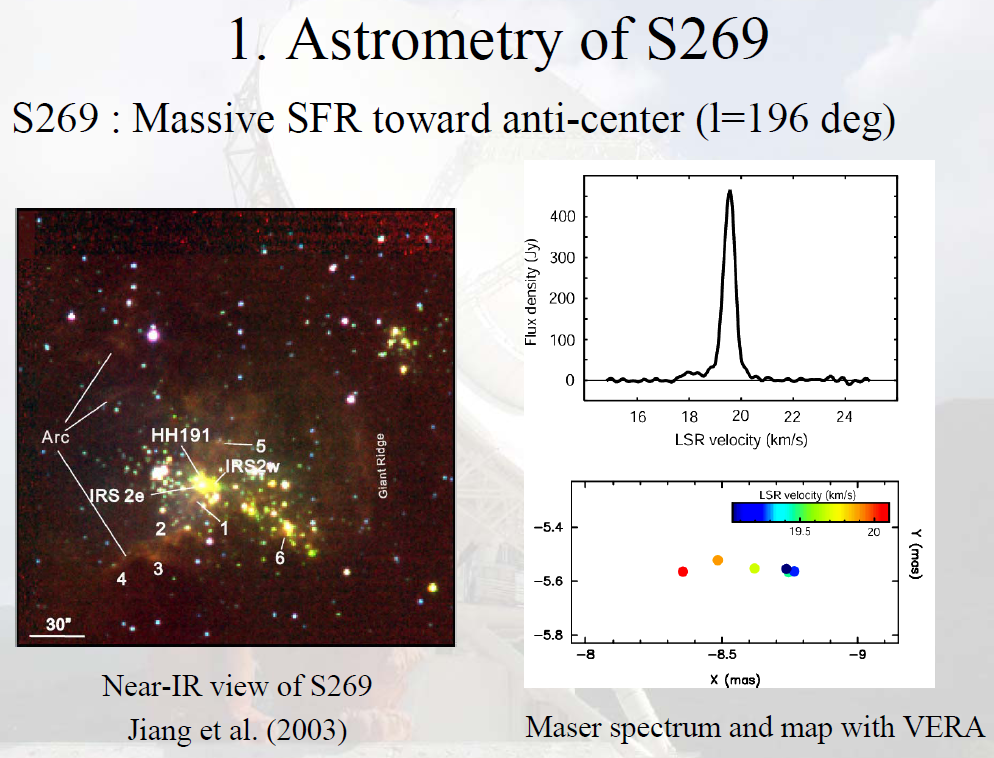
Image taken from
a presentation by Mareki Honma, NAOJ
If one measures the position of one of these masers over a period of several years, one will see an intriguing pattern. Shown below are VERA measurements of a maser in the Orion-KL region; the figure shows the Right Ascension component of the position as a function of time.
Figure taken from
a presentation by Mareki Honma, NAOJ ;
I've erased the parallax result so that my students can't
peek at it in class.
Q: What is the parallax to Orion KL
based on the measurements above?
Q: What is the distance to Orion KL?
A slightly more recent measurement by VERA yields the even more precise parallax to Orion-KL of
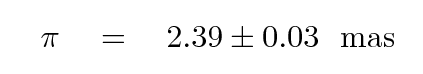
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.