
A picture of the transit of 1882, from the US Naval Observatory's Rare Books collection
 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
On June 8, 2004, some lucky people will see the planet Venus pass over the face of the Sun. Here in Rochester, if the weather permits, we will see the very end of the event: Venus will takes its leave of the solar disk just after the Sun rises above the horizon.

A picture of the transit of 1882, from the
US Naval Observatory's Rare Books collection
Over the next hour, I will look at transits of Venus from several different perspectives. I'll pretend to be a newspaper reporter and follow the standard questions one asks about a story:
Astronomers (and their governments) spent a great deal of time, effort, and money sending expeditions to the far corners of the globe to observe the previous four transits. They realized that transits of Venus hold a key to determining the size of the entire solar system and all its planets. I'll spend most of my talk today describing how one can use geometry and measurements of a transit to find the distance between the Earth and Venus; and how that can be extended to determine the scale of all bodies in the solar system.
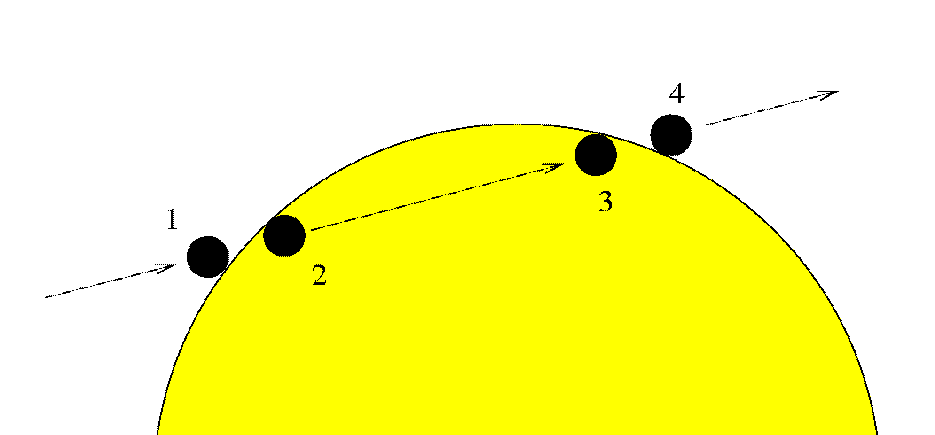
Astronomically speaking, a transit occurs when Venus passes in front of any part of the Sun's disk as seen from the Earth:
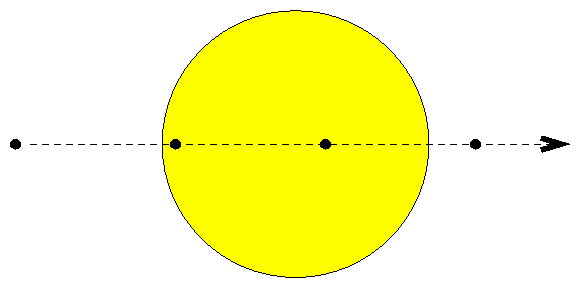
Now, since Venus is closer to the Sun than the Earth, it might seem logical that every time it passes us in its orbit, we ought to see a transit.


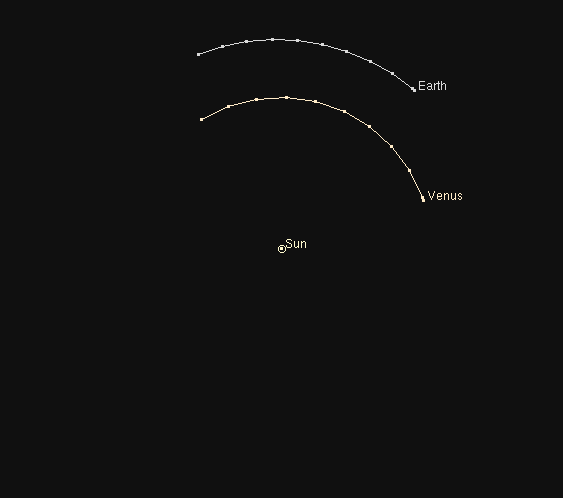
Unfortunately, the orbit of Venus is tilted by about 3.4 degrees relative to the orbit of the Earth.
That means that most of the time, Venus passes above or below the Sun in the sky. For example, in January, 2002, observers on the Earth would have seen this (had they been able to detect Venus in the daytime sky):
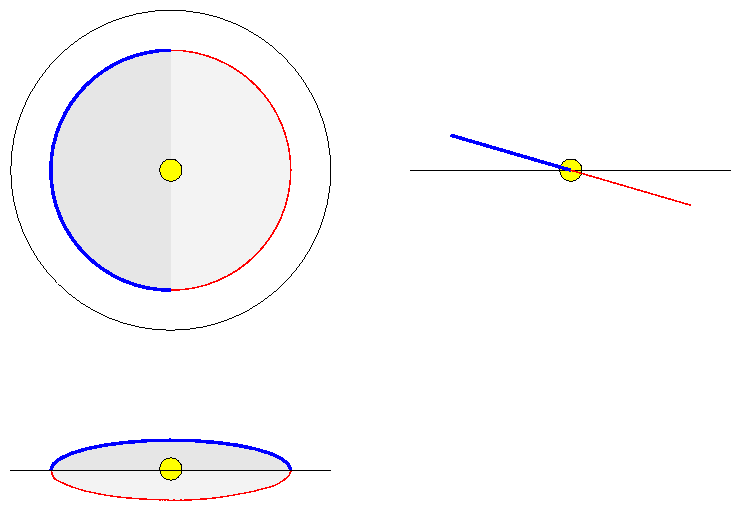
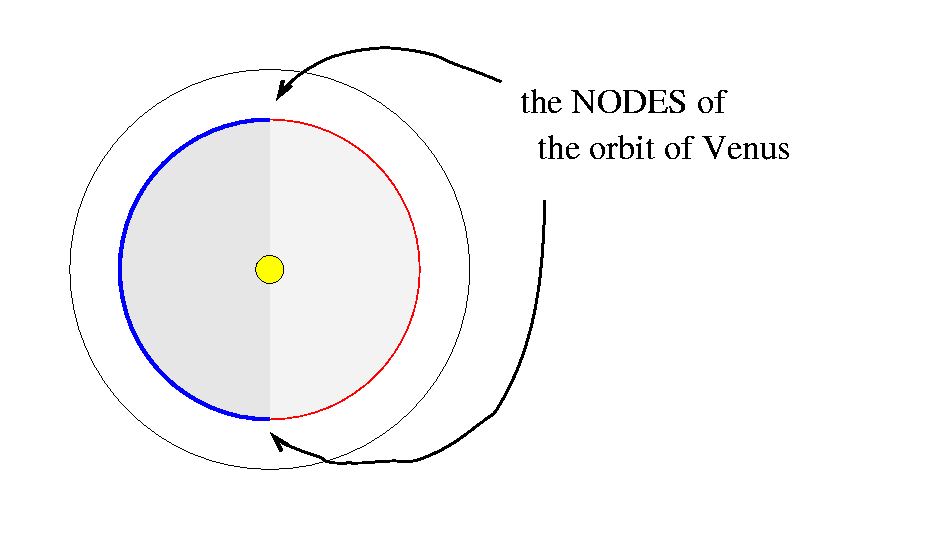
Although the orbit of Venus is tilted relative to that of the Earth, there are two special places, called nodes, at which it crosses the plane of the Earth's orbit.
If Venus happens to be moving through one of the nodes of its orbit at the same time that it passes the Earth, we will see a transit.
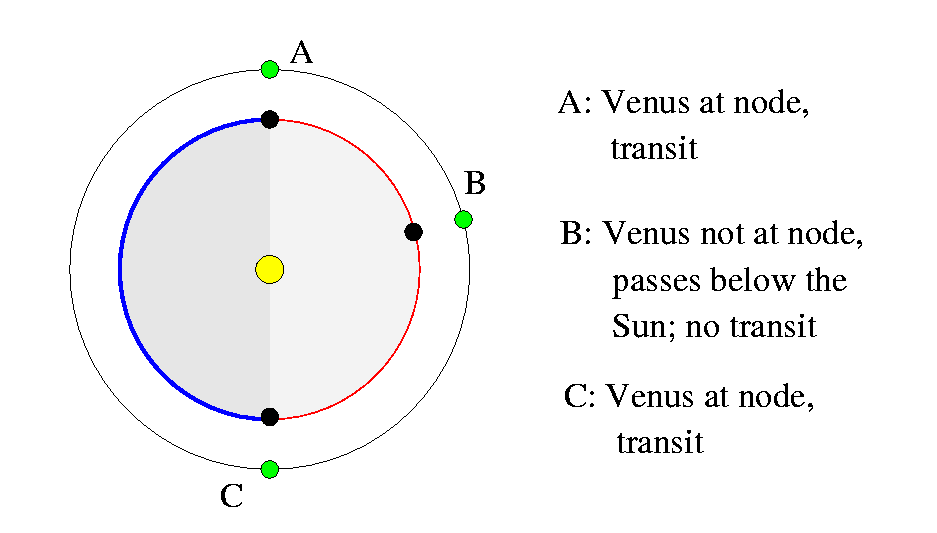
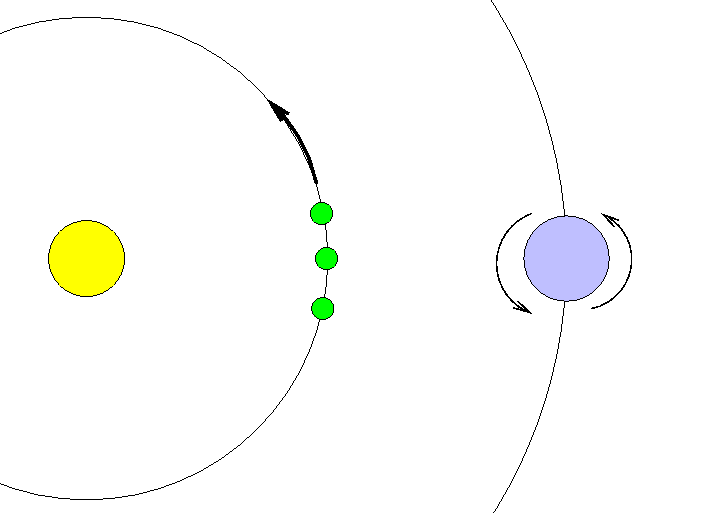
The question is, how often does this special alignment occur? Let's use a little math to find out. We'll approximate both orbits as circles, and assume that the planets move around those circles with uniform speed.
Period of Venus: Pv = 225 days
Period of Earth: Pe = 365 days
Q1: How long between occasions when Venus passes
the Earth it its orbit?
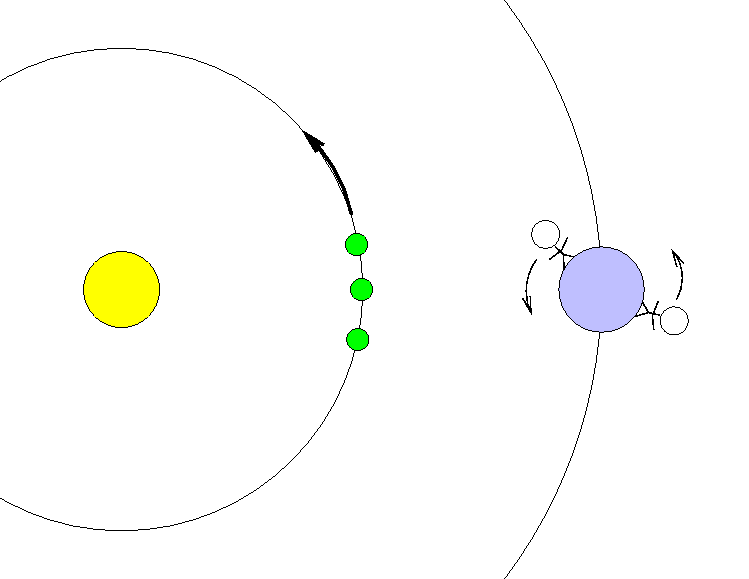
There is a small zone around each node in which Venus is close enough to the node that it will move in front of the Sun's disk as it passes the Earth. The width of each zone is about 3.3 degrees, and note that there are two zones, one around each node.
Q2: What fraction of the time will Venus
pass the Earth inside one of these zones?
Q3: Estimate the time between successive
transits of Venus -- if they were
all uncorrelated with each other.
But, of course, the motions of Venus and the Earth do follow strict physical laws, and so the times of their conjunctions are not uncorrelated. It turns out that the current orbital conditions cause pairs of transits to occur roughly 8 years apart, followed by long gaps of about 120 years.
Recent (and future) transits of Venus
Dec 7, 1631 Dec 24, 1639
June 6, 1761 June 3, 1769
Dec 8, 1874 Dec 6, 1882
June 8, 2004 June 6, 2012
Just why are these rare transits of Venus such a big deal? It turns out that one can use them as the key to unlock the mystery of the size of our solar system. Let me explain by starting at the beginning, with the first attempts to measure celestial distances.
Distances in the solar system: before Kepler
The first step to determining the size of the solar system is to figure out the size of the Earth. The Greek astronomer Eratosthenes made the earliest good quantitative measurement in the late third century BC. By comparing the shadows cast simultaneously by objects at Alexandria and at Syene, he was able to determine their difference in latitude. Since he also knew the distance along the surface of the Earth between these two cities, he was able to calculate the circumference of the Earth, and thus its diameter.
The Greeks were also able to estimate the distance from the Earth to the Moon reasonably well; in fact, they knew the distance to the Moon in terms of the Earth's diameter years before Eratosthenes gave them an absolute size with which they could find an absolute distance to the Moon.
Knowing the RELATIVE distances between celestial bodies, but lacking a single ABSOLUTE distance to set the physical scale, is exactly where astronomers would be again two millenia later ....
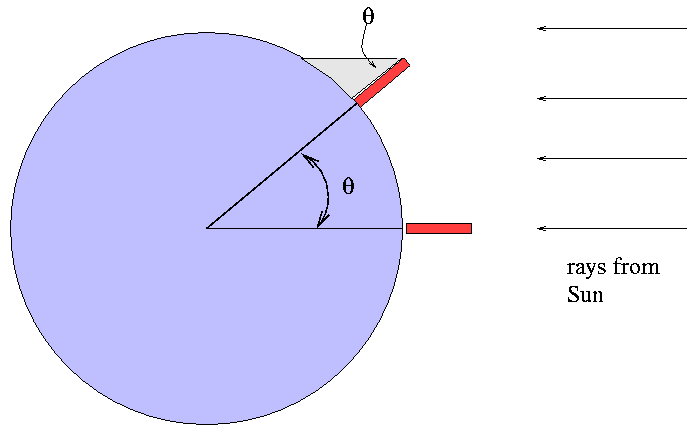
Aristarchos of Samos in the early third century BC considered eclipses of the Moon, in which the Earth passes between the Sun and Moon and covers the Moon with its shadow:
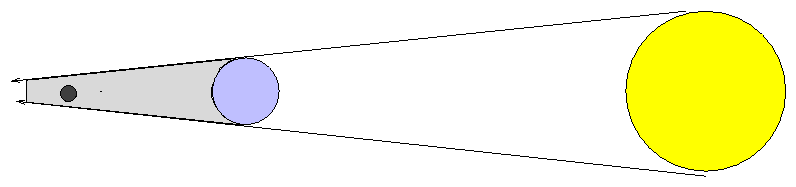
Nothing in this diagram is drawn to scale.
From the size of the Earth's shadow relative to the Moon, Aristarchos estimated that the Moon was about one-third the size of the Earth. A careful observer can easily measure the apparent angular size of the Moon to be about one half of a degree. If one knows the size of the Earth, a bit of trigonometry will then reveal the distance to the Moon.
Apparently, Aristarchos was more interested in theory than in observations, since his value for the Moon's angular diameter was two degrees -- four times too large!
To be fair, Aristarchos adopts in later writing the figure of half a degree for the Moon's angular size, which is within the the actual range.But roughly one hundred years later, in the middle of the second century BC, Hipparchus set the record straight. His very careful measurements yielded a distance between the Earth and Moon of 59 Earth radii. Together with Eratosthenes' size of the Earth, this gives a distance of 376,000 kilometers, well within the actual range of the Moon's orbit.
However, when the Greek astronomers attempted to jump to a much larger distance, between the Earth and the Sun, they failed miserably. Aristarchos described an idea which looked good on paper, but didn't work well at all. He realized that if the Sun is at an infinite distance from the Earth and Moon, then a first-quarter Moon -- when exactly half of the visible disk of the Moon is illuminated -- will occur when the Sun and Moon are exactly 90 degrees apart in the sky.
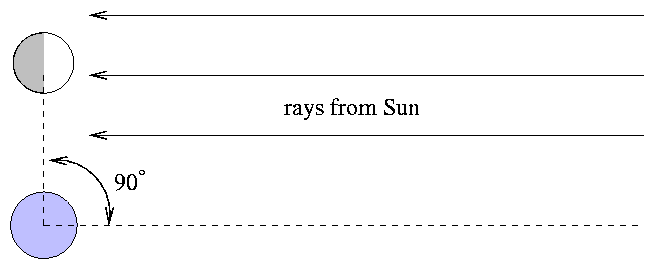
This diagram isn't drawn to scale, either.
But if the Sun is NOT at infinity, the first-quarter Moon will be slightly less than 90 degrees away from the Sun. The small angular difference can be used to calculate the distance from the Earth to the Sun in terms of the Earth-Moon distance.
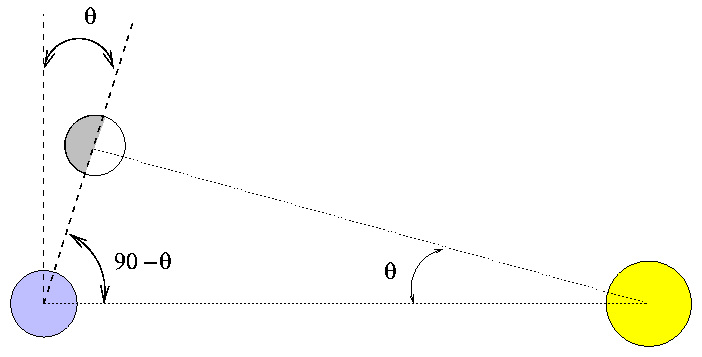
Nor is this diagram.
The trouble with this method is
Aristarchos measured a separation of (90 - θ) = 87 degrees at first quarter, rather than the actual (90 - θ) = 89.85 degrees. As a result, he calculated the Sun to be only twenty times the Moon's distance from the Earth, rather than the actual factor four hundred.
Later Greek astronomers made more accurate measurements, which increased their estimates of the distance of the Sun, but they still didn't come close to the actual value. One of the best estimates, from Ptolemy, puts the Sun about 7.5 million km from the Earth.
Distances in the solar system: Kepler
In the late sixteenth century, Danish astronomer Tycho Brahe set up the world's most sophisticated (naked-eye) observatory and amassed an enormous number of accurate positional measurements of stars and planets. He was able to demonstrate that comets were not, as Aristotle had claimed, disturbances in the Earth's own atmosphere, but were instead located in space far from the Earth, many times more distant than the Moon. His goal was to use his observations to create an improved model of the solar system. He hired a brilliant young man, Johannes Kepler, to act as his assistant in this task. When Brahe died, in 1601, Kepler inherited his catalogs and continued the project.
Because Tycho's instruments and methods were so much better than any ever used before, Kepler was able to discern subtle features in the motions of the planets which had escaped all previous astronomers. As he studied the orbit of Mars, in particular, he gradually began to see that a few very simple rules would explain all the complicated behavior. In 1609, in his book Commentaries on the Motions of Mars, he wrote down what we now call his First and Second Laws of Planetary Motions:
Ten years later, as he was about to send to the printers the final manuscript for his book Harmonia Mundi ("The Harmony of the World"), Kepler realized that there was yet another, much more beautiful, facet to the dance of the planets:
" ...if you want the exact moment in time, it [the correct form of the law] was conceived mentally on 8th March in this year one thousand six hundred and eighteen, but submitted to calculation in an unlucky way, and therefore rejected as false, and finally returning on the 15th of May and adopting a new line of attack, stormed the darkness of my mind. So strong was the support from the combination of my labour of seventeen years on the observations of Brahe and the present study, which conspired together, that at first I believed I was dreaming, and assuming my conclusion among my basic premises. But it is absolutely certain and exact that the proportion between the periodic times of any two planets is precisely the sesquialterate proportion of their mean distances..."
[Harmony of the World, Linz, 1619]
The word sesquialterate means "raised to the three-halves power." Kepler's Third Law is most commonly written in a slightly different manner:
2 3
Period = (const) * (semi-major axis)
Now, a key feature of this relationship is that
it expresses the relative sizes of the planetary
orbits in terms of their periods.
Sizes and distances are hard to measure,
but periods are easy:
just count the days it takes Mars (or Mercury,
or Saturn) to move all the way around
the sky, using the stars as a reference.
For example, suppose that Jupiter is currently
close to the bright star Regulus in Leo.
Over a period of several months, you can see
it slowly slide eastward in the sky, away
from Regulus.
If you wait long enough -- about twelve years --
Jupiter will complete its journey through the
constellations and return to Regulus.
Yes, yes, the Earth is also moving over the course of these twelve years, so it takes a bit more work to isolate the motion of Jupiter alone. But it still isn't too hard.
Best of all, it is easy to improve the precision of your estimate of the period: just keep watching and keep counting. Averaging over many revolutions will yield a very precise period.
"Wait a minute," some of you might cry at this point, "how did Kepler do that? If he didn't know the distances to the planets, how could he state that those distances followed this mathematical relationship?" Well, that's a good question. Just how did Kepler figure this out? The answer was probably something like this:
Compare, for example, the relative sizes of planetary orbits Kepler derived from Tycho's observations to our best current measurements. The values are expressed as Kepler described them, with the semimajor axis of the Earth's orbit having a size of 1000 units. See chapters 4 and 9 of Book Five of the "Harmony".
Planet Based on Tycho's obs Based on harmonies Actual values peri aph peri aph peri aph Mercury 307 470 308 476 307 467 Venus 719 729 716 726 718 728 Earth 982 1018 983 1017 983 1017 Mars 1382 1665 1384 1661 1381 1666 Jupiter 4949 5451 4948 5464 4952 5455 Saturn 8968 10052 8994 10118 9021 10054
He was certainly correct, but Kepler may have gone a bit overboard when he wrote about this rule
Res est certissima exactissimaque, ...
Still, after seventeen years of painstaking, tedious calculation, he was entitled to a bit of hyperbole.
Armed with Kepler's Third Law, astronomers could turn their very accurate periods for each planet into accurate relative distances. The usual convention was to use the Earth's orbit as a measuring stick, and express the orbital sizes of other planets in terms of the Astronomical Unit:
Planet Orbital period Orbital semi-major axis
(years) (AU)
----------------------------------------------------
Mercury 0.241 0.387
Venus 0.615 0.723
Earth 1.0 1.0
Mars 1.88 1.52
Jupiter 11.86 5.20
Saturn 29.46 9.55
----------------------------------------------------
To put it another way, astronomers could draw an accurate picture of the solar system ....
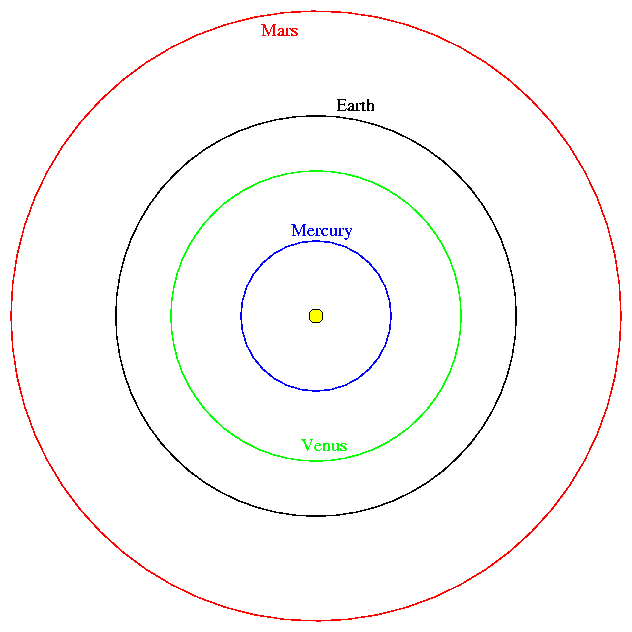
but they couldn't tell you the scale of the diagram.
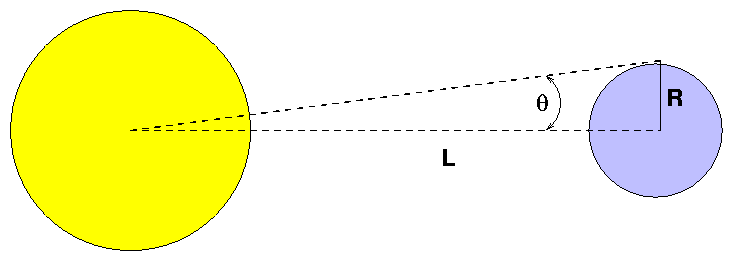
Note that if one could determine just ONE distance in absolute terms -- whether the real size of any planet's orbit, or even the real distance between two planets at some point in time -- then one could turn this relative set of distances into an absolute set of distances. The distance between the Earth and Sun is as good as any. Since (as we shall see shortly) most methods of finding this distance relied upon trigonometric parallax, this was often described as "finding the solar parallax."
Using transits of Venus to find the solar parallax: theory
In the most basic terms, a transit of Venus permits scientists on Earth to draw a big triangle in the sky:
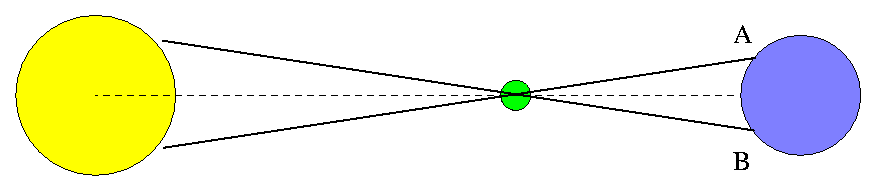
All information in this diagram has been ruthlessly
altered for clarity.
People at different locations on Earth will see Venus move across the Sun's disk on slightly different paths.
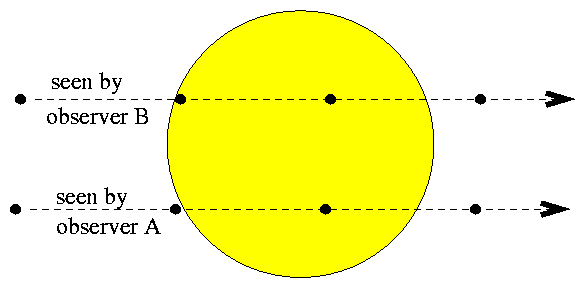
The difference in apparent paths is so-o-o-o exaggerated in
this diagram ....
So, in theory, finding the distance between the Earth and Sun -- the "solar parallax" -- is pretty simple:

Practical difficulties in observing transits
It seems easy to use Venus to find this crucial distance, but in real life, things aren't so simple. There are several factors which make it a really difficult experiment to perform, of which the most fundamental are
Astronomers were well aware of all these difficulties, which is why they devised two strategies for observing a transit which might nonetheless yield accurate results.
Edmund Halley was one of the first to understand the importance of transits.
In 1716, he urged his fellow astronomers to plan ahead
for the coming transits of 1761 and 1769,
knowing that he would not live to see either one.
He knew that it would be difficult to synchronize
measurements made thousands of miles apart around
the world, and that the shift in position of Venus'
path would be hard to measure.
Therefore, he came up with a plan which
relied on measurements of
the duration of the transit,
which required only a local clock running at a standard rate.
He described how observers at different locations should
measure the period from second to third contacts:
Observers at different latitudes ought to see transits
of different lengths, which would require different
amounts of time to occur.
But Halley very cleverly realized that there was a SECOND
reason for the transits durations to vary, due to
the rotation of the Earth.
Consider a frame moving with the Earth in its orbit around
the Sun;
Venus catches up to the Earth and passes it.
Note that the direction of Earth's rotation is
the same as the direction of both planets' revolution around the Sun.
That means that
"Wait a minute," you may now cry,
"that may be true, but how can it help with
the measurements? If someone is on the
nighttime side of the Earth, how can he
see the Sun?"
The crucial point is that the rotational axis
of the Earth is not perpendicular to the plane
of its orbit, but inclined by roughly 23 degrees.
That means that observers near the Earth's poles
may be able to see the Sun continuously,
for 24 hours a day.
Of course, someone exactly on a pole won't
receive any motion due to the rotation of the Earth;
but there will be a "sweet spot"
where the rotational lengthening of the
transit duration is maximized.
By a nice coincidence,
transits of Venus currently occur during the months of June
or December, when the Earth's rotational
axis is tilted in exactly the right
direction to give Halley's method its maximum effect
for some transits.
You can see that this method will work best
if the polar observer
is also situated so that he sees the transit
occur closer to the Sun's center
than other observers.
The two effects -- increased path length across
the Sun, and slower apparent angular speed of Venus --
will add together to make his measured duration
last much longer than those of other observers.
This happy coincidence occurs about half the time.
Under favorable circumstances,
two observers may measure a
difference in duration
of up to fifteen or twenty minutes
over the course of a five-hour transit.
That is clearly an effect which one
ought to be able to measure with
some precision.
Halley hoped that with a measurements
good to a couple of seconds, astronomers might
determine the distance to Venus
with an accuracy of one-fifth of one percent.
In the years before the transit of 1761,
the French astronomer Joseph Nicolas Delisle
suggested a different approach to the problem.
He thought that a more "classical"
geometric method would yield better
results, especially for certain transits.
His method sounds straightforward:
Note that this method requires that observers
know their longitudes accurately.
In the eighteenth century,
mapmakers and geographers were still
struggling with the problem of longitudes.
While the longitudes of the major European
cities were known reasonably well,
those of obscure islands in the Pacific --
from which the transit was best observed --
were not.
In addition,
Delisle's technique requires that
the absolute time of each event in the transit
be recorded.
The first accurate chronometers would not be
widely available until years after
the transits of 1761 and 1769.
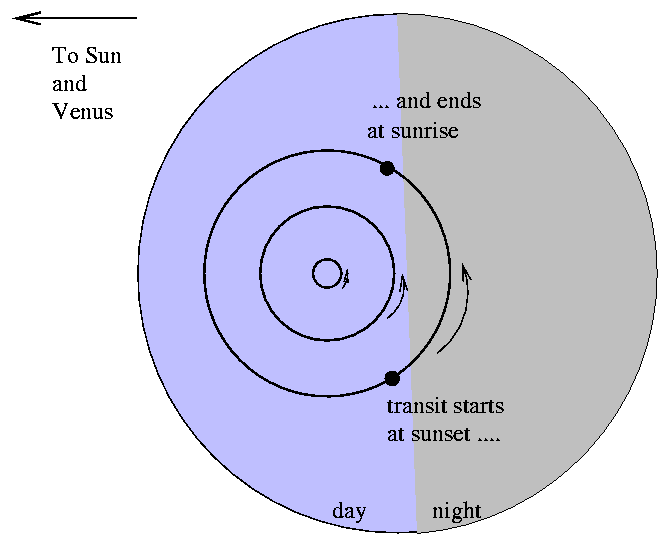
Where best to put the observers?
Let's look again at the sequence of events
in a transit, as viewed from the Earth:
Now switch the point of view:
instead of standing on the Earth and looking at
the Sun,
stand on the Sun and look outwards at the Earth.
Just before the transit begins,
the shadow (*) cast by Venus will lie off to one side
of the Earth:
Where the shadow first touches the Earth, an
observer would see and measure second contact:
As Venus moves across the face of the Sun,
its shadow will eventually touch the other
side of the Earth;
observers stationed there will NOW measure
second contact at their location.
After several hours pass, the shadow will start
to leave the Earth,
causing one set of observers to record
third contact.
And finally,
the shadow will leave the other side of the Earth,
leading the last observers
to record their third contact.
If we zoom in on the Earth at these critical moments,
we can see where to place observers
for the maximum difference in
recorded times (which will yield the longest
possible baselines).
The best places from which to see second contact are:
And the best places for observers of third contact are:
European countries and scientific societies
organized a great set of expeditions
to measure the transits of 1761 and 1769,
and another bunch to measure the transits of 1874
and 1882.
You may know more about these efforts than you realize.
Captain Cook, for example,
was sent by the British Navy to the island of Tahiti
in order to observe the transit of 1769,
which was best seen from
the South Pacific.
Actually, the real, secret reason for Cook's
first voyage was the British government's
desire to claim the rumored "Southern Continent" (Australia)
which Cook did succeed in discovering and mapping.
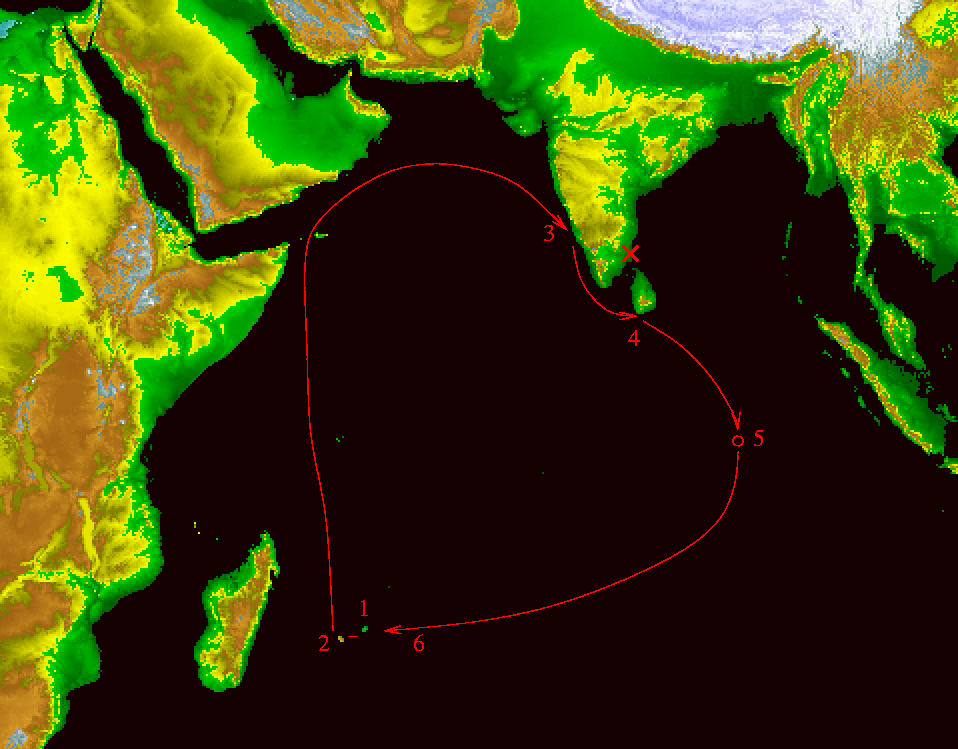
One of the saddest stories belongs to the French astronomer
Guillaume Le Gentil.
He set out from France on March 26, 1760,
to observe the transit of June 6, 1761, from Pondicherry, India.
After about three and a half months at sea,
he arrived at Isle de France (now called Mauritius)
on July 10, 1760. He still had nearly eleven
months to reach his assigned location
on the southeastern coast of the Indian peninsula.
He had some difficulty finding a ship which could take
him to Pondicherry, and so it wasn't until
March 11, 1761, that he set off from Isle de France.
Le Gentil was discouraged that he had travelled
halfway around the world for nothing ...
but did he give up? No!
He determined to stay in that part of the world
and wait there for the NEXT
transit of Venus, on June 3, 1769,
eight years later.
He spent his time fruitfully,
travelling around the Indian Ocean and making (in his words)
As the time of the next transit (June 3, 1769) approached,
Le Gentil decided to make Pondicherry his
base of operations.
He arrived in that city in March 27, 1768.
The governor kindly gave Le Gentil permission to set
up an observatory at any spot he found best.
Le Gentil decided on the remains of a palace
which had been destroyed in the war.
The local militia used the basement of this tower
as a storeroom.
Strangely enough, Le Gentil was not bothered by
sitting on top of sixty thousand weight of gunpowder!
With the help of the governor, Le Gentil managed
to start regular observations in July, 1768;
his first action was to establish very accurately the latitude
and longitude of Pondicherry.
The transit was predicted to occur early on the morning
of June 4 (local time and date).
Le Gentil writes that the morning skies were beautiful
during the entire month of May, and for the first two
days of June;
but during the night before the transit, the
weather turned.
A squall passed through the region, covering
the skies with clouds.
During the entire transit, it was impossible
to see the Sun at all.
Just two hours later,
though, the front passed and revealed
the Sun again.
Le Gentil had failed again.
He wrote in his journal,
"I was unable to recover from my astonishment, I had difficulty
in realizing that the transit of Venus was finally over ...
At length I was more than two weeks in a singular dejection
and almost did not have the
courage to take up my pen to continue my journal;
and several times it fell
from my hands, when the moment came to report to France the fate of my
operations."
After another two years of travel,
he managed to return home to France
in 1771, eleven years after he had left.
He found his house robbed and his estate looted
by greedy relatives who claimed he had died.
Sigh.
Another little historical note: in 1882, Louis Swift (a professor at
the University of Rochester, just a few miles from where I now
work at RIT) attempted to observe the transit from
the Warner Observatory on East Avenue:
Swift's 16-inch refractor was one of the largest
instruments in the area, but it was
powerless to see through the clouds which swept
over the region.
Swift recorded three brief glimpses of the Sun
during the entire transit, of no scientific use.
I could have warned him that would happen :-(
Just how well were astronomers able to
determine the distance to the Sun via
these transits of Venus?
The usual way of summarizing one's calculations
was to quote the
horizontal parallax of the Sun:
in essence, the angle that the Earth's equatorial radius
would subtend if observed from the center of the Sun
(at a time when the Earth was one AU from the Sun).
The value is written in arcseconds:
one arcsecond is 1/3600 of a degree.
I found a compilation of results from the
observed transits in an article by William Harkness,
in Appendix III of
Washingon Observations for 1885.
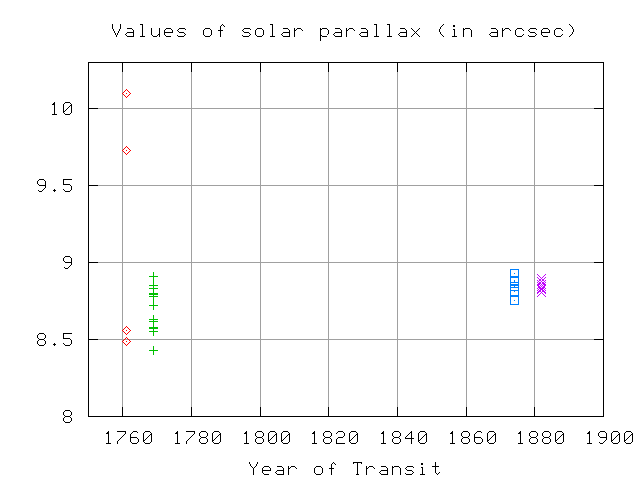
You can see the values converge from the earliest transits to the
most recent:
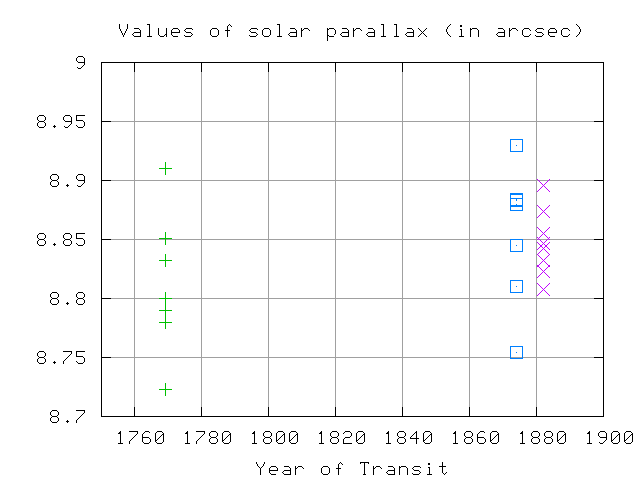
A closeup shows that the average value for the transits of 1874 and 1882
was around 8.84 arcseconds:
The modern-day value is (a drum roll, please) 8.79 arcseconds.
The results from the nineteenth century transits
were just a little bit too large,
about 0.4 percent too high.
Just a few years after the 1882 transit,
in 1900, astronomers around the world coordinated
their efforts to find the distance to the newly discovered
asteroid Eros at its opposition.
Eros would pass 0.32 AU from the Earth,
slightly farther than Venus,
but appear as a tiny pinpoint of light surrounded by stars
of similar brightness;
thus, one could make more accurate measurements of its
position relative to a good reference frame than
one could of the fuzzy disk of Venus against the featureless
background of the Sun.
The result was a value of about 8.81 arcseconds.
Is there any scientific reason to observe the transits of 2004 and 2012?
No.
We can now bounce radio waves off the planet Venus
(and other planets, too),
measuring its distance to a matter of kilometers,
far better than any observations of a transit can do.
However,
it may be fun.
Just hope for clear skies to the East when the
Sun rises on June 8!
Last modified 3/25/2008 by MWR
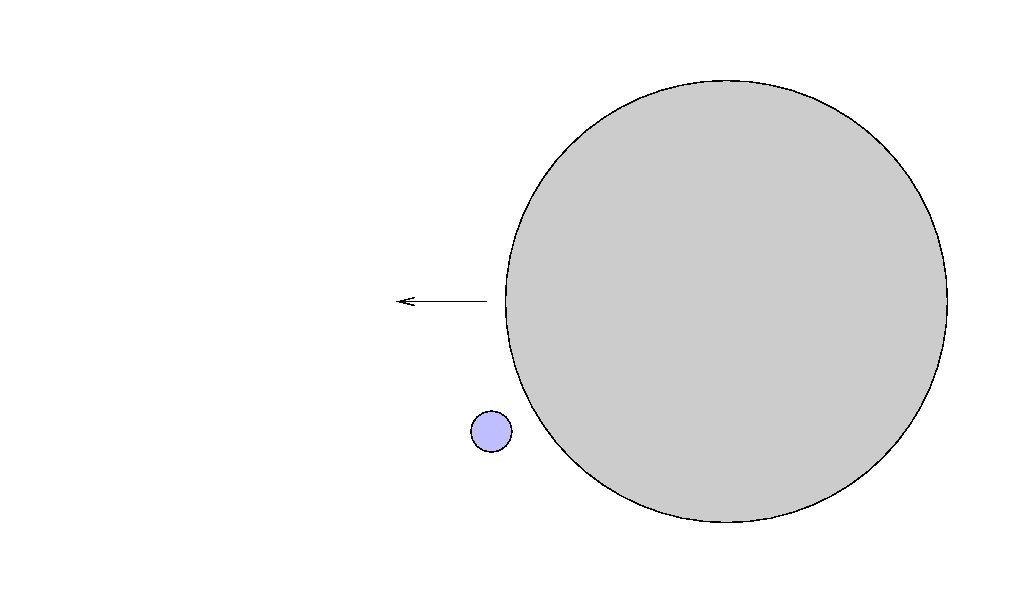
Halley's method: measure the duration

Yes, this is exaggerated again for clarity
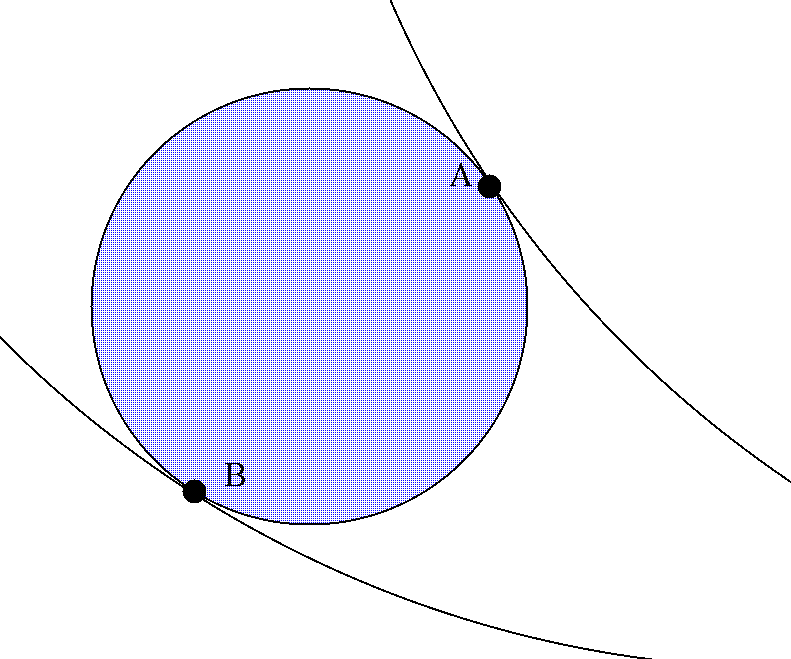
Delisle's method: measure absolute times of second and third contacts

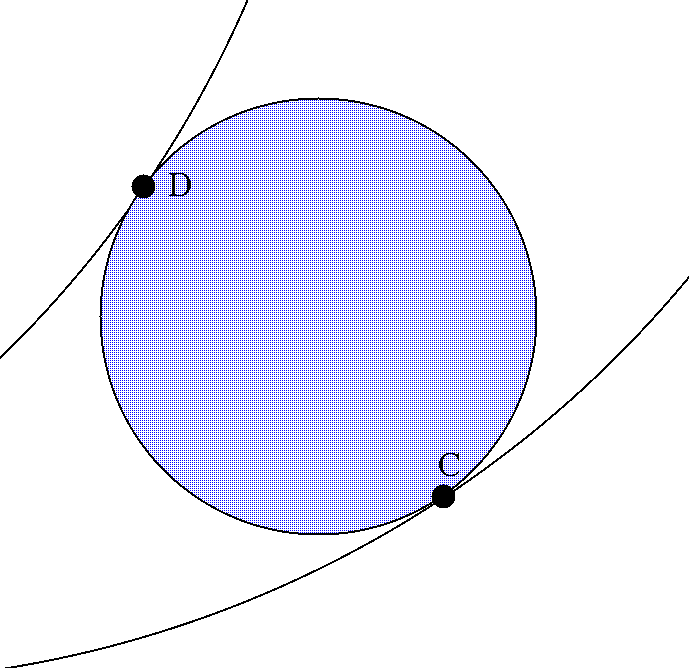
(*) This is the "interior" shadow of Venus;
one can define a larger, "exterior" shadow for first
and fourth contacts




A little history
all the observations I could on geography,
natural history, physics, astronomy, navigation,
winds and tides.

"This is the fate which often awaits astronomers.
I had gone more than ten thousand leagues; it seemed
that I had crossed such a great expanse of seas,
exiling myself from my native land,
only to be the spectator of a fatal cloud
which came to place itself before the sun at the precise
moment of my observation, to carry off from me the fruits
of my pains and of my fatigues....

The results
Transit of 1761
1763 Hornsby 9.73
1765 Short 8.56
1765 Pingre 10.10
1767 Planman 8.49
Transit of 1769
1769 Euler 8.80
1771 Hornsby 8.78
1771 LaLande 8.62
1771 Maskelyne 8.723
1772 Lexell 8.63
1772 Pingre 8.80
1772 Planman 8.43
1786 DuSejour 8.851
1814 Delambre 8.552
1815 Ferrer 8.58
1865 Powalky 8.832
1868 Stone 8.91
Transits of 1761 and 1769 combined
1835 Encke 8.571
Transit of 1874
1877 Airy 8.754 British timings
1878 Stone 8.884 " "
1878 Tupman 8.846 " "
1881 Puiseux 8.93 French observations
1881 Stone 8.88 +/- 0.02 " "
1881 Todd 8.883 +/- 0.034 American photographs
1885 Obrecht 8.81 +/- 0.06 French daguerreotypes
Transit of 1882
1887 Stone 8.832 +/- 0.024
1887 Cruls 8.808
1882 Harkness 8.847 +/- 0.012 American photographs
A brief digression about other methods of determining
the distance to the Sun: transits of Venus weren't the
only way astronomers tried to find the scale of the solar
system. It is possible to use simultaneous (or nearly simultaneous)
observations of other bodies in a similar fashion.
Mars was used as far back as 1672 by Cassini, and its opposition
of 1877 provided several estimates. Harkness (1885) provides
an average value of 8.844 arcseconds for the solar parallax
based on measurements of Mars. Astronomers also tried
using asteroids for this purpose; Harkness quotes a value
of 8.819 arcseconds as the average of several attempts.
So transits of Venus were an important, but not unique, opportunity
to find the size of the solar system.
For more information
 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.