Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Determining the distances of celestial objects is fundamental to understanding what they are:
But, in practice, measuring the distance to a star or a galaxy is very, very difficult. Astronomers are clever and inventive people; they have devised a number of schemes which at least provide some reasonable guesses at distances. But you should be aware of the number of approximations and the uncertainty in the whole enterprise.
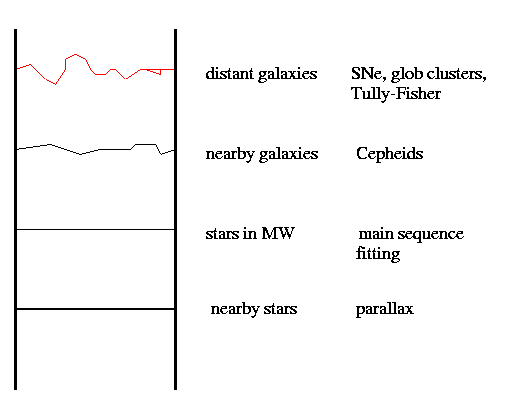
In general, we can measure most precisely the distances to objects which are closest to us; the farther away we look, the worse our estimates become. In order to gauge distances to very distant objects, we use nearby objects as standards. We end up with a cosmological distance ladder, in which the secure, bottom rungs are distances to nearby stars, and the very shaky, very uncertain top rungs are distances to quasars halfway across the universe:
We'll start off, today, with a description of parallax, a very accurate method we can apply to our nearest stellar neighbors.
One of the few reliable methods astronomers may use to determine the distances to objects in space is called parallax. It is based on trigonometry, so let's start with that.
There are special mathematical tools one can use to determine the lengths of the sides of a right triangle. In the figure below, suppose that we want to know the distance L.
If we can measure the side B, and the angle alpha, then we can use the equation
B
L = ----------
tan(alpha)
to calculate L.
We can use the same method for a situation in which there are two such triangles, back-to-back:
We can still figure out the distance L with trigonometry. Once again, we calculate
B
L = ----------
tan(alpha)
but we could also describe this as
1/2 (2B)
L = --------------------
tan [ 1/2 (2*alpha) ]
or
half of the total baseline
L = ----------------------------
tan [ half the total angle ]
How does this help astronomers measure the distance to nearby stars? Well, the Earth orbits around the Sun once a year. Since the Earth is about R = 1.5 x 10^(11) meters away from the Sun, the total baseline distance by which the Earth moves is about 2 R = 3.0 x 10^(11) meters. If we look at a star once in January, and again six months later in July when the Earth has moved to the other side of its orbit, we might see the star move slightly, relative to more distant stars in the background:
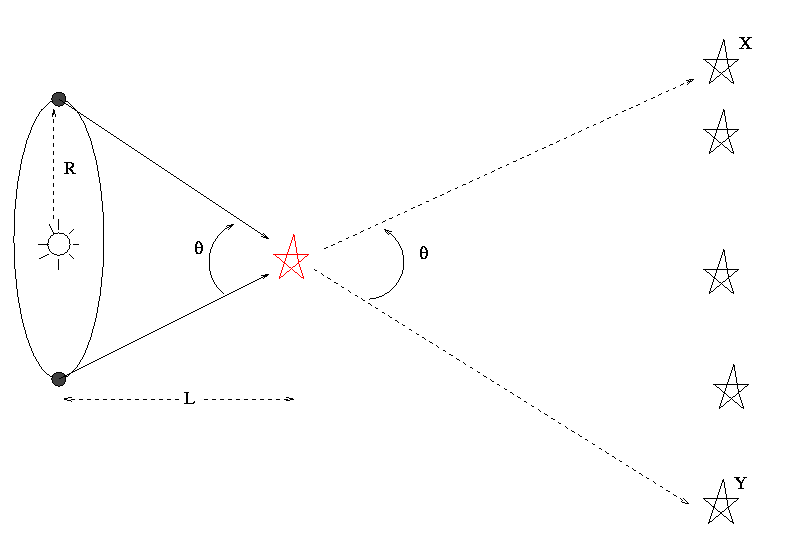
If we can measure the angle theta by which the star appears to shift, we can calculate the distance L to the star:
half of total baseline
L = ---------------------------
tan [ half of total angle ]
R
= ----------------
tan [ theta/2 ]
It seems like a simple problem -- just measure the position of a star at several times during the year, when the Earth is at different positions in its orbit, and determine the size of the shift. Unfortunately, there are a number of complications.
The result is that, even in the best cases, we must try to detect shifts which are a small fraction of the apparent visible extent of a star. Try it yourself on the images below. The images were created so that
First, a simulation of the parallax of a star which is at a distance of 1 pc (closer to our Sun than any real star). Click on the image to see the view 6 months apart.
The very best Earth-bound (single) telescopes, working patiently over decades, are able to measure accurately shifts of about 0.003 arcseconds. Ordinary optical observations do much worse than that, with errors more typically 0.05 arcsec, or worse!
And there's another complication, too:
European astronomers designed a satellite specifically to measure the parallax of nearby stars.
Hipparcos operated in a somewhat peculiar fashion: it had two mirrors, mounted at an angle of about 58 degrees. The mirrors sent light from two patches of the sky, 58 degrees apart, onto a single detector. The detector looked at both patches simultaneously, and therefore measured
The Hipparcos satellite spun slowly in space, scanning strips of the sky as it rotated.
Over the course of 3 years in orbit, Hipparcos made millions of measurements of thousands of stars. It measured the motion of each star about 100 to 150 times:
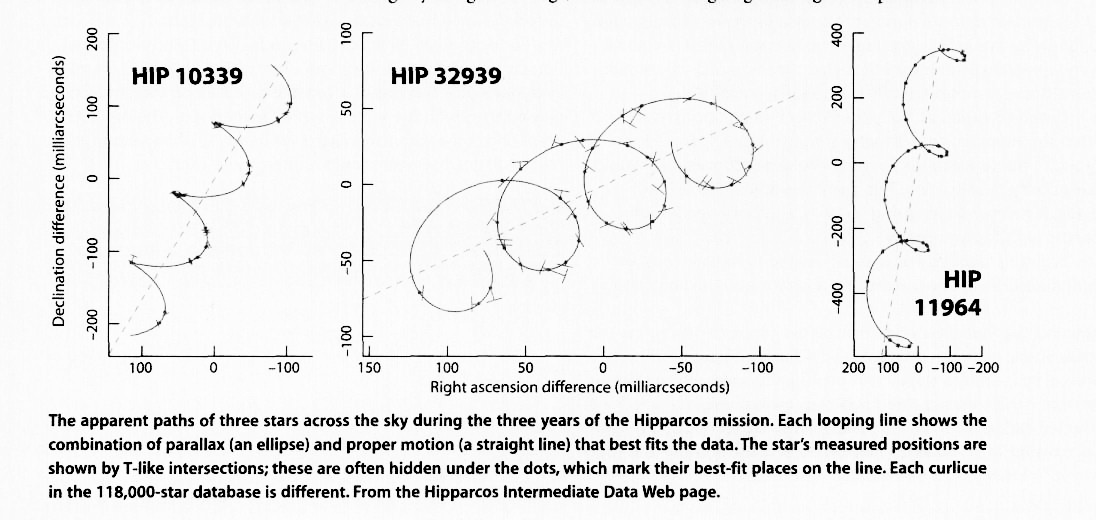
From these measurements, it was able to detect
The measurements made by Hipparcos were about ten times more precise than those made by most ground-based telescopes. In addition, Hipparcos was able to measure over 100,000 stars, which was way, way more than all the astronomers in the history of the science had been able to do from the ground. It was a real breakthrough.
The Pleiades cluster is one of the closest open clusters of stars. You can see it in the sky on winter nights: just follow Orion's belt to the upper right. When Hipparcos looked at the stars in this area of the sky, it found that many of the stars share a common proper motion :
The Hipparcos satellite looked at stars again and again and again, over a three-year period. It measured the brightness of each star over 100 times during this interval. Some of the stars varied in brightness:
For more information, see
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.