Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
| Did you know that astronomers have discovered another "moon" of Earth? |
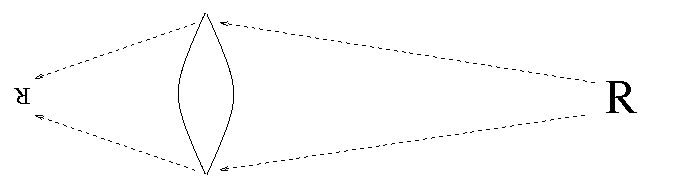
What is a lens? It's a piece of glass or other transparent material shaped so that light rays which pass through it are "bent", or diverted from their original paths:
Light rays "bend" when they pass through a transparent material because they travel a bit slower inside the material. Is there any other way to "bend" light rays?
Yes! Gravity can alter the path of light rays, too. A black hole, after all, is simply an object with a gravitational field so strong that even photons are unable to escape from its vicinity. Any light ray which attempts to fly outwards from a black hole is stopped, and turned back into the black hole. That's an extreme case of "bending."
Q: Do you recall how to compute the critical distance, called the
"event horizon", from which light cannot escape
from a black hole?
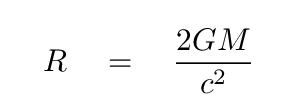
where
So, a star lies directly behind a black hole, and some of the starlight travels directly toward the black hole, it will fall in and never escape.
But there are more modest situations, in which the photon isn't stopped dead, but merely nudged a bit so that its direction (and energy) change slightly. For example, if the ray of light doesn't head straight into the black hole, but is aimed so that the impact parameter b is larger than the radius of the black hole,
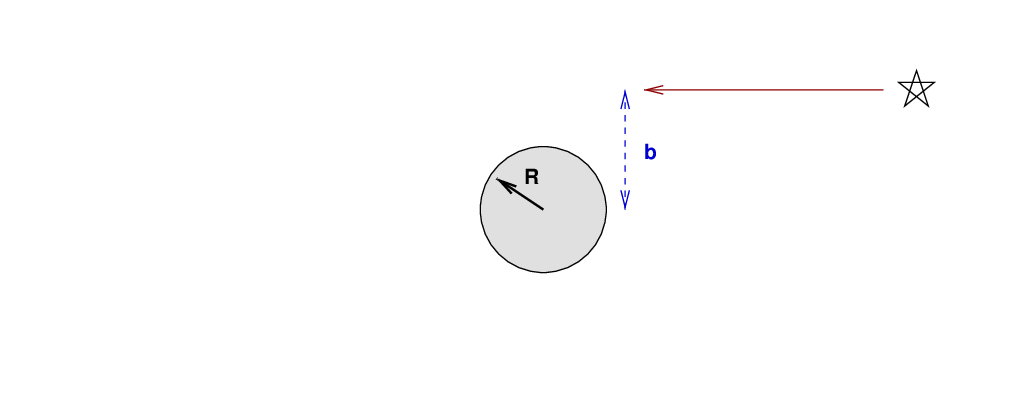
then we might expect the ray of light to continue in a straight line.
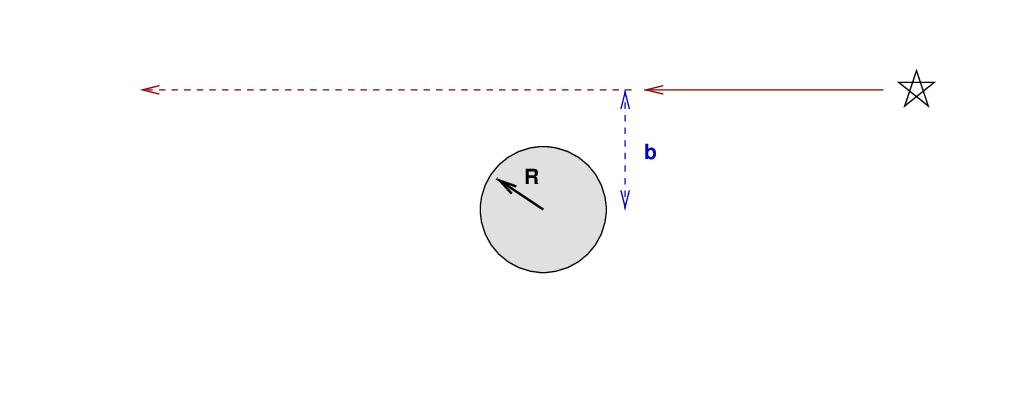
But -- it doesn't. The gravitational influence of the black hole will cause the direction of the ray to change slightly, "bending" it in a manner similar to the way a lens bends rays of light. We could describe this deflection by the angle θ, which measures the change in the ray's direction,
The angle θ by which the light ray is deflected depends on two factors: its closest approach to the massive object (called the impact parameter, and denoted by b in the diagram), and the mass of the lensing object, M. As you might guess, it takes both a very massive lens, and a very close approach, to cause any significant deflection.
If an intervening mass lines up perfectly with a background source, it can bend the light from the source which would otherwise go far above us to come down to us; and bend the light which would otherwise go far below us to come up to us.
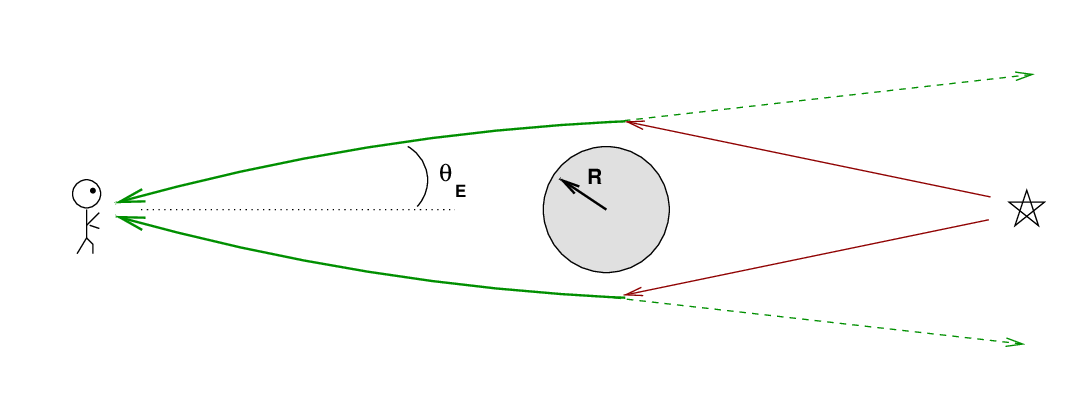
To us, it looks like there is light coming from an angle θE above the actual source ... and from an angle θE below the actual source ... and, in fact, from an angle θE to the left, and the to the right, and everywhere in between. The result is that we see a ring of light surrounding the actual position of the source:
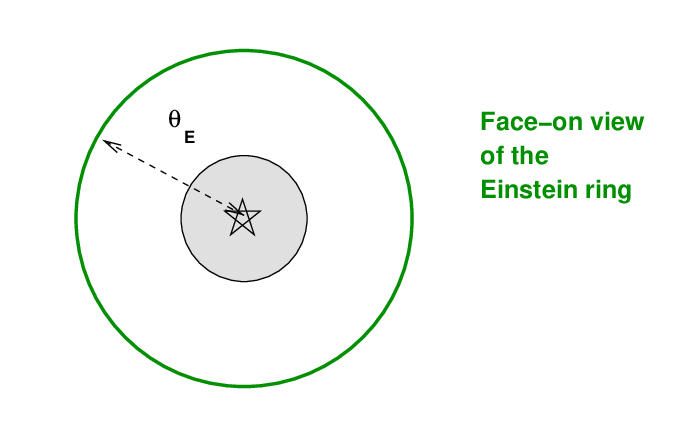
The angle θE is called the Einstein ring radius, because Albert Einstein was the first to figure out that -- in the very unlikely event that a faint, massive object lined up exactly in front of a bright, background source -- we might see a bright ring of deflected light.
The Einstein ring radius depends on the mass of the lensing object: the more massive it is, the larger the Einstein ring radius. It also depends on the distance between us, the lensing object, and the background source. Gravitational lensing is most effective (meaning the ring radius is largest) when the lensing object is half way between us the and background source. In that special case, the Einstein ring radius is given by this equation:
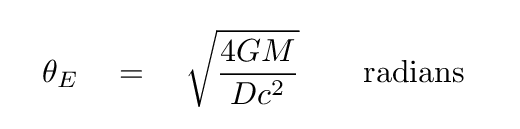
where
G = gravitational constant
= 6.67 x 10^(-11) N*kg^2/m^2
M = mass of lensing object, in kg
D = distance from us to lens (and lens to source), in meters
c = speed of light
= 3 x 10^8 m/s
This turns out to be pretty darn small.
mass of lensing object distance Einstein ring radius
(parsecs) (m) arcseconds
--------------------------------------------------------------------------
lensed by a star
1 solar mass 100 3 x 1018
(2 x 1030 kg) 1,000 3 x 1019
10,000 3 x 1020
lensed by a galaxy
1012 solar 100 Mpc 3 x 1024
(2 x 1042 kg) 1,000 Mpc 3 x 1025
10,000 Mpc 3 x 1026
lensed by galaxy cluster
1015 solar 1,000 Mpc 3 x 1025
(2 x 1045 kg) 10,000 Mpc 3 x 1026
100,000 Mpc 3 x 1027
--------------------------------------------------------------------------
The very idea that the direction of light rays might be bent by gravitational fields is rather counterintuitive. Even if one accepts the idea, the SIZE of the effect is small -- really, really small. How could one even test this hypothesis?
Soon after Einstein published his theory of general relativity in 1915, some astronomers realized that there WAS a situation in which they might be able to observe this effect: a solar eclipse! During a total solar eclipse, the Moon covers the Sun's disk entirely, causing the sky to grow dark, almost as dark as night. It ought to be possible to take photographs showing stars which are close to the edge of the Sun's disk: close enough, perhaps, for the deflection of the light rays from distant stars to be detected.
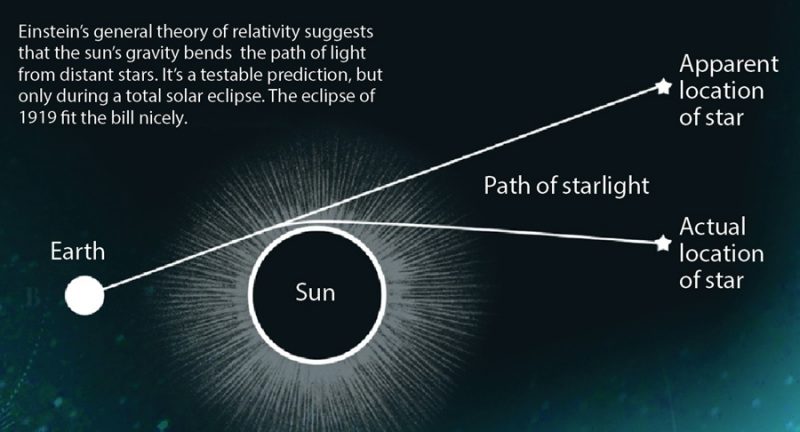
Image courtesy of
GSFC/ NASA/ DiscoverMagazine.com.
We can't use the formula above to compute the size of the deflections, because the Sun is certainly NOT halfway between the Earth and the distant stars. There is a more complex version of the formula, however, which one can use, and the astronomers of the early twentieth century did so.
The plan was to take two sets of photographs of one particular area of the sky -- the area in which the Sun and Moon would appear during the eclipse. The first set of pictures would be taken months before (or after) the eclipse, when this region would appear at night.
Image near the region of eclipse of 2017 created thanks to
Months later (or earlier), astronomers would take a second set of photographs of the same area of the sky during the eclipse.
Image near the region of eclipse of 2017 created thanks to
If one could measure the positions of the stars in each set of images very, very carefully, then one might detect a subtle shift in their positions: during the eclipse photo, stars would appear to move AWAY from the Sun. Those closest to the Sun would appear to shift by the largest amount, and those farther away by smaller angles.
Image near the region of eclipse of 2017 created thanks to
Doesn't look so hard to measure, does it? Well, my previous diagram was slightly exaggerating the size of those angular shifts in position ....
Image near the region of eclipse of 2017 created thanks to
This turns out to be a difficult experiment, especially if one must carry glass photographic plates thousands of miles across the globe and set up telescopes and cameras in a wilderness. The first few attempts did detect a radial shift in position of stars close to the Sun, but the size of the shift was rather uncertain. You can read many accounts of a famous expedition made in 1919, just after the end of the First World War.
In modern times, on the other hand, with improvements in imaging technology and computational resources, it is a much more manageable task. For example, consider the example of amateur astronomer Donald Bruns.
Image courtesy of
Steve Lang and Sky and Telescope
In 2016 and 2017, Bruns practiced taking pictures of the region of the sky in which an eclipse would take place on August 21, 2017. He predicted the size of the shifts he ought to see; the units on the horizontal axis are "solar radii". Note that the expected shifts are at most just one arcsecond.
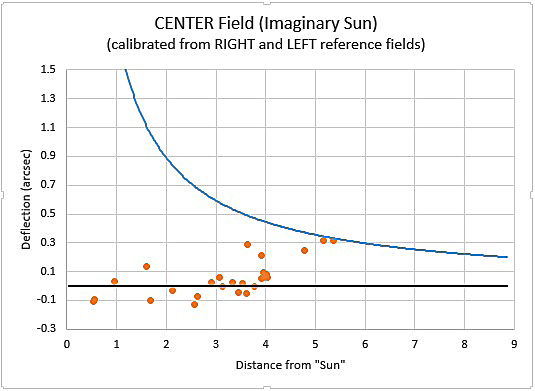
Image courtesy of
Donald Bruns and Sky and Telescope
He worked on reducing sources of random and systematic errors in his equipment and analysis, and was blessed with good weather during the eclipse. His results are a striking confirmation that Einstein's theory is correct.
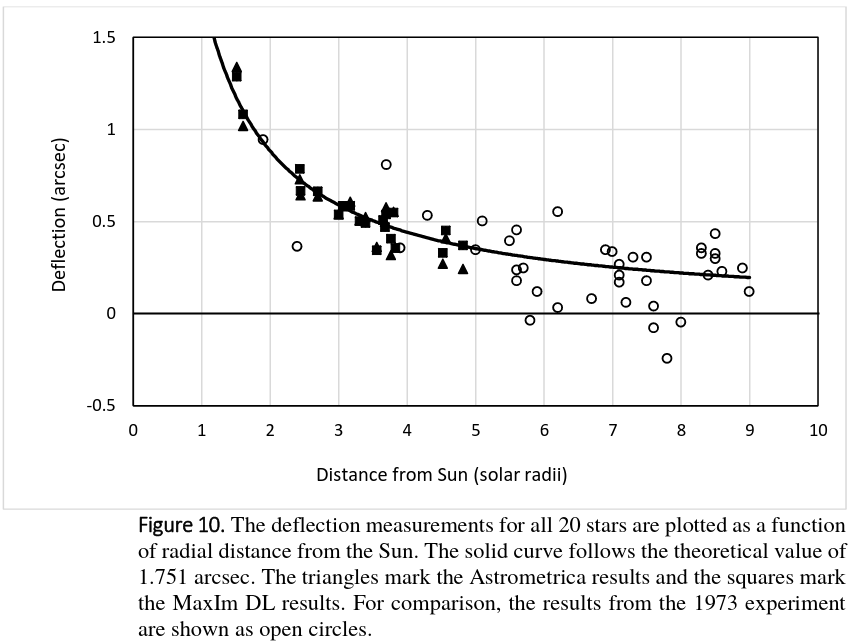
Figure 10 taken from
Bruns, Classical and Quantum Gravity, 35, 7 (2018)
Back in 1919 (or soon thereafter), astronomers first detected the lensing of distant stars due to the gravitational influence of the Sun. And, for a number of decades afterward, the Sun was the only "lens" that produced a signal big enough for us to measure.
Several scientists had pointed out that we might someday discover instances of one distant star acting as a lens for another, more distant star; but that would require the two stars to line up nearly PERFECTLY from our point of view. It was, literally, a one-in-a-million-chance, and so no one bothered to look for it. The amount of work required was so large, and the chances of success so small, so that it just didn't make sense.
Taken from
Einstein, A., Science, 84, 506 (1936)
But as computers and computer-controlled telescopes developed together in the 1970s and 1980s, several groups of astronomers realized that it was becoming possible to automate most of the work. The goal of these microlensing searches was to monitor rich fields of stars over and over and over, night after night, year after year, measuring the brightness of millions of stars carefully. The hope was that we might catch one of those nearly perfect alignments in the act, as a nearby star slowly drifted past a more distant one.
Gravitational lensing theory predicted that IF the background star should come within the Einstein Ring radius of the lensing star, the lensing distortion would increase the size of the background star ... which would in turn increase its brightness. Our telescopes would not see the weird stretched-out shapes caused by lensing, but they would see the increase in brightness.
(Click on the image to activate animation)
Image and movie courtesy of
David Specht / Eamonn Kerins / University of Manchester
(Click on the image to activate animation)
Image and movie courtesy of
Gravitational Lensing Group at the Max Planck Institute for Astrophysics
How much would the background star appear to brighten? That would depend on how close it came to the foreground lensing object. In a nutshell, if the background star's separation reaches the Einstein Ring radius, its intensity increases significantly.
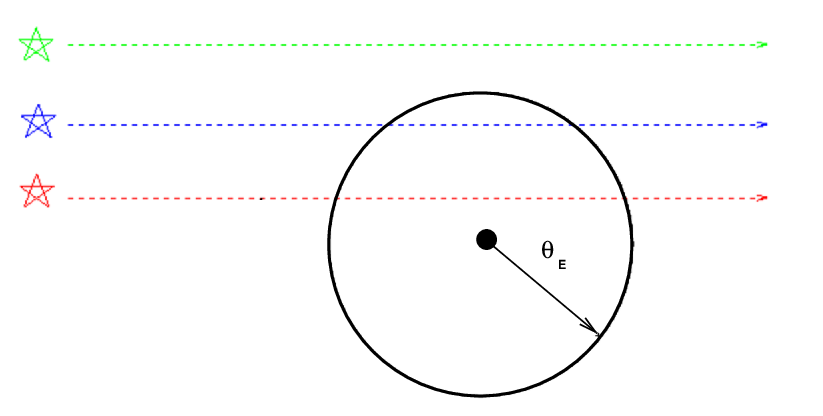
Here's a table with some representative values:
u = b/θE max amplification
--------------------------------------------
5.0 1.00 no brighter
4.0 1.01
3.0 1.02
2.0 1.06
1.5 1.13
1.2 1.23 green star in figure
1.0 1.34
0.8 1.53 blue star in figure
0.5 2.18
0.2 5.07 red star in figure
0.1 10.04
--------------------------------------------
As a star passes behind a lensing object, its light gradually becomes brighter and brighter. Its brightness peaks when the star is at its closest approach to the lensing object, then fades again as it moves away. The shape of this light curve is very distinctive:
Over a decade or so, one team after another found cases of microlensing.
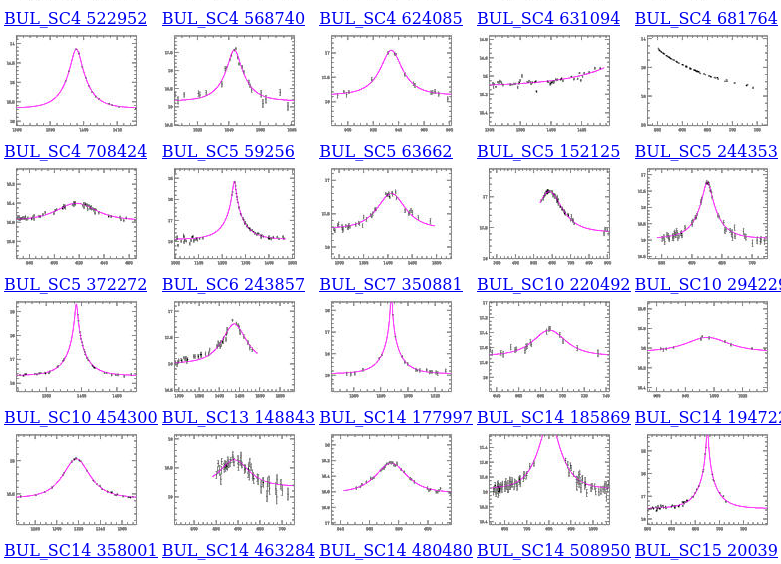
Light curves courtesy of
The OGLE collaboration
By studying these cases of star-on-star microlensing, astronomers can learn about stellar populations in our galaxy (and in the Magellanic Clouds), place limits on the number of MACHOs in the galactic halo, and study certain properties in the outer atmospheres of distant stars. There are also occasional surprises.
Consider the case of OGLE 2005-BLG-390Lb, one of the many lensing events found by the OGLE group. Click on the picture below to watch a short animation of the brightness of stars in a small field over the course of a month or so.
Image and animation courtesy of
OGLE / Danish 1.54m telescope / Daniel Kubas
Did you catch that brief flash near the end?
Image courtesy of
OGLA/MOA/PLANET/RoboNET
That short, small, increase in brightness was caused by a planet orbiting the lensing star. The gravitational field of the lensing star deflected the light rays of the background star by a considerably amount, making it brighten by about a factor of three over the course of a month. The much smaller gravitational field of the planet led to a smaller increase in brightness (only about 20%) which lasted less than a day.
Click on the image below to watch an animation of the event.
Image and animation courtesy of
Andrew Williams, University of Western Australia / David Bennett, University of Notre Dame
At the current time, NASA's Exoplanet Archive contains information on 592 planets circling other stars which have been detected by microlensing.
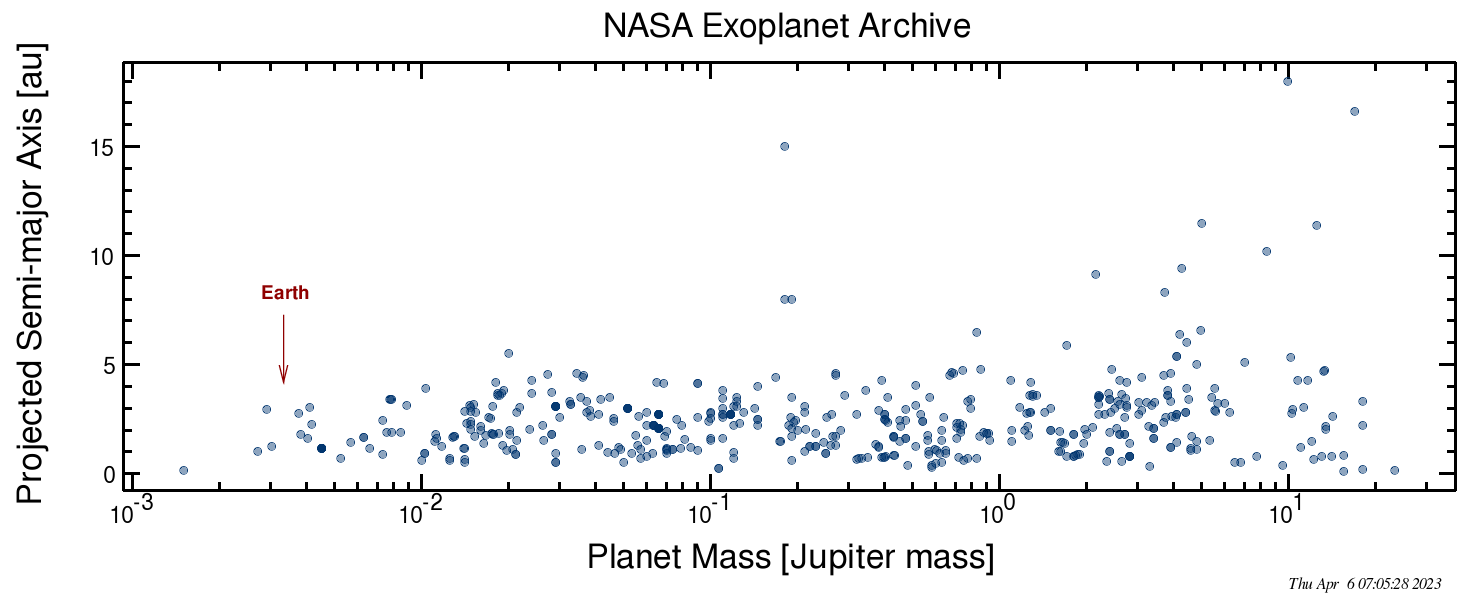
Graph created using tools and data provided by
the NASA Exoplanet Archive
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.