Creative Commons License Copyright © Michael Richmond. This work is licensed under a Creative Commons License.

Gravitational Lensing Theory

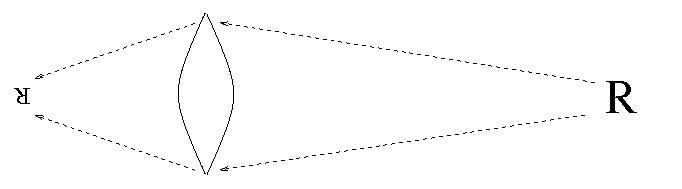
What is a lens? It's a piece of glass or other transparent material shaped so that light rays which pass through it are "bent", or diverted from their original paths:

Light rays "bend" when they pass through a transparent material because they travel a bit slower inside the material. Is there any other way to "bend" light rays?

Yes! Gravity can alter the path of light rays, too. A black hole, after all, is simply an object with a gravitational field so strong that even photons are unable to escape from its vicinity. Any light ray which attempts to fly outwards from a black hole is stopped, and turned back into the black hole. That's an extreme case of "bending."

But there are more modest situations, in which the photon isn't stopped dead, but merely nudged a bit so that its direction (and energy) change slightly. For example, if we place a very massive object near the path of an incoming light ray:

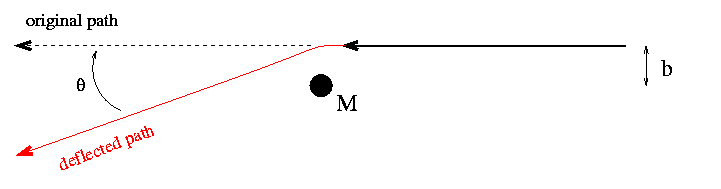
The angle theta by which the light ray is deflected depends on two factors: its closest approach to the massive object (called the impact parameter, and denoted by b in the diagram), and the mass of the lensing object, M. As you might guess, it takes both a very massive lens, and a very close approach, to cause any significant deflection.

If an intervening mass lines up perfectly with a background source, it can bend the light from the source which would otherwise go far above us to come to us; and bend the light which would otherwise go far below us to come to us.

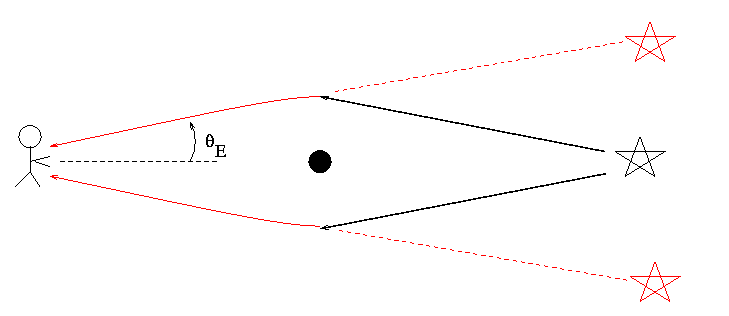
To us, it looks like there is light coming from an angle theta E above the actual source ... and from an angle theta E below the actual source ... and, in fact, from an angle theta E to the left, and the to the right, and everywhere in between. The result is that we see a ring of light surrounding the actual position of the source:

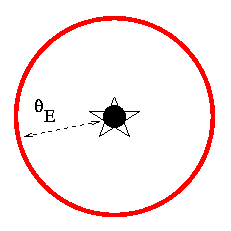
The angle theta E is called the Einstein ring radius, because Albert Einstein was the first to figure out that -- in the very unlikely event that a faint, massive object lined up exactly in front of a bright, background source -- we might see a bright ring of deflected light.

The Einstein ring radius depends on the mass of the lensing object: the more massive it is, the larger the Einstein ring radius. It also depends on the distance between us, the lensing object, and the background source. Gravitational lensing is most effective (meaning the ring radius is largest) when the lensing object is half way between us the and background source. In that event, the Einstein ring radius is given by this equation: 

                           4GM
    theta E    =   sqrt [ ----- ]
                          D c^2
where 
    G    =     gravitational constant   
         =     6.67 x 10^(-11)  N*kg^2/m^2

    M    =     mass of lensing object, in kg

    D    =     distance from us to lens (and lens to source), in m

    c    =     speed of light
         =     3 x 10^8 m/s

This turns out to be pretty darn small. 

mass of lensing object    distance         Einstein ring radius
 (solar masses)          (parsecs)       degrees      arcseconds
--------------------------------------------------------------------
lensed by a star
       1                    100         0.0000025      0.0089
                          1,000         0.00000078     0.0028
                         10,000         0.00000025     0.00089

lensed by a galaxy
    1 x 10^12           100 Mpc         0.0025         8.9
                      1,000 Mpc         0.00078        2.9
                     10,000 Mpc         0.00025        0.89

lensed by a galaxy cluster
    1 x 10^15         1,000 Mpc         0.025         89
                     10,000 Mpc         0.0078        28
                    100,000 Mpc         0.0025         8.9

When astronomers take pictures with optical or infrared telescopes, the smallest features they can see are about 

       0.000028 degrees  =  0.1 arcsec
From the table above, it's clear that we have no hope of seeing a ring of light due to lensing by a single star -- it would be just too small. But it does seem possible that we might discern an Einstein ring if a galaxy, or even better, many galaxies, should act as a lens.

And, in fact, astronomers have found such cases!

Now, if the lensing object isn't lined up exactly with the background source, then we don't see a bright ring of light; instead, we see a distorted, magnified version of the background source. The closer the lens and background source line up, the brighter and more distorted the image of the background source. If the two line up well enough that the true position of the background source falls within the Einstein ring radius of the lens, then multiple images appear!

The Gravitational Lensing Group at the Max Planck Institute for Astrophysics in Germany has created some Quicktime movies showing the effects of gravitational lensing in different situations:

Jim Lovell of the University of Tasmania provides another animation of lensing in action. This animated GIF shows how a spiral galaxy can bend the light of a background object -- in this case, a quasar, as seen by a radio telescope. The yellow ring represents the Einstein ring radius of the galaxy.

Note that in some situations, when a background source passes very close to the center of a lens, a set of large, stretched-out, arc-like images may be created. And that's exactly what we see in a number of rich, massive clusters of galaxies:

Notice that all the examples above involve galaxies -- collections of billions of stars. I haven't shown any instances of one star lensing another. Why not? As the table above shows, the Einstein ring radius for single star is tiny -- which means that the chances are very small that another star might be lined up well enough to show any significant distortion. The chances are so small that Einstein himself, when he described gravitational lensing in 1936, wrote that this was just a theoretical curiosity; he didn't expect that astronomers would see such a rare event.

And, indeed, for many decades, he was right. We would have to look at millions and millions of stars to have a good chance of finding an alignment close enough to cause a visible effect.....

For more information, see

Creative Commons License Copyright © Michael Richmond. This work is licensed under a Creative Commons License.