
Image courtesy of David Hardy and PPARC.
 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Today, we'll look at the evolution of "high-mass" stars -- those which start their lives with more than 5 solar masses. As you will see, these massive stars tend to go out with a bang.
But first, we'll take a second look at one rare, but spectacular, ending for low-mass stars which have reached the white dwarf stage of their evolution. Under the right circumstances, these low-mass stars can also provide fireworks.
In our previous class, we saw how low-mass stars (like the Sun) evolve once they leave the main sequence: they move up the red-giant branch, undergo a core helium flash, slide back down and sit for quite a while on the red clump/horizontal branch. Then, after building up a core of carbon and oxygen, a series of shell helium flashes push off the outer envelope, creating a planetary nebula and leaving behind a white dwarf. Under ordinary circumstances, the white dwarf will very slowly cool down and gently, quietly, fade to black.
However, there are rare exceptions to this general rule. The key is the nature of the electron degeneracy pressure that supports white dwarfs. Although this strange quantum phenomenon can provide much stronger resistance to compression than ordinary electromagnetic forces, it does have its limit. In 1931, an astronomer named Subrahmanyan Chandrasekhar showed that electron degeneracy cannot support a white dwarf if its mass exceeds a particular value. In his honor, that critical mass, M ≈ 1.44 solar masses, is known as the Chandrasekhar limit.
Suppose that a white dwarf with a mass close to this limit is formed when a star with initial mass greater than the Sun passes through its red-giant and planetary-nebula phases. No problem. But suppose further than the white dwarf is part of a close binary star system, in which its partner is an ordinary main-sequence star. If those two objects should happen to orbit each other at a small distance, then gas from the ordinary star's outer atmosphere might be pulled off and fall onto the white dwarf.

Image courtesy of
David Hardy and PPARC.
We observe quite a few binary star systems of this sort, which are known as cataclysmic variable stars. Actually, _I_ observe them, myself, using the equipment at the RIT Observatory. Most of the time, very little gas is transferred to the white dwarf, but every now and then, a whole bunch will flow for a few days -- and then the system flares up in brightness by factors of a thousand or so.
Anyway, if the parameters of one of these binary systems are just right, hydrogen gas from the ordinary star's atmosphere will eventually pile up on the surface of the white dwarf, INCREASING ITS MASS. Over a long period, the mass of the white dwarf might reach the Chandrasekhar limit.
Then what happens?
As the mass of the white dwarf increases, the gravitational pressure on its central region grows larger and larger. The density and temperature of the core increase, too. At some point, around a temperature of 600-700 million Kelvin, carbon fusion reactions will start to take place; for example,
Each reaction of this sort will produce some energy, due to the binding energy of the heavier nuclei created in the process.
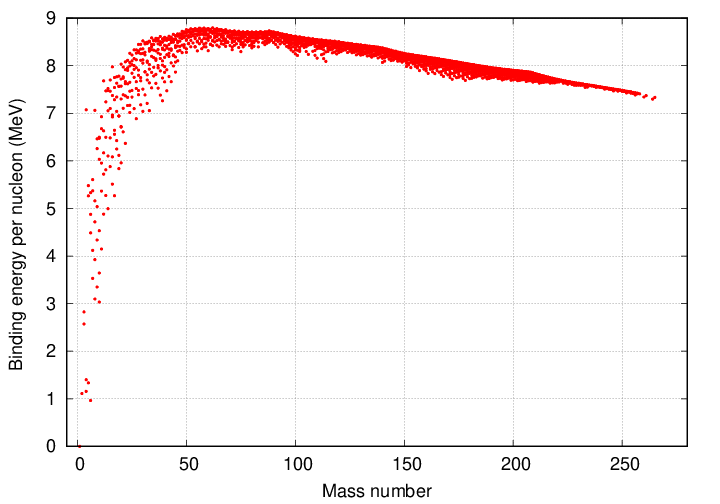
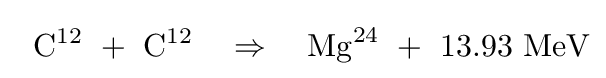
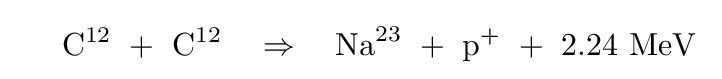
Q: Using the graph below, estimate the energy released, in MeV per
nucleon, when Carbon-12 combines to form Magnesium-24.
Then multiply by the number of nucleons involved in the input
products to find the total energy released in one fusion.
How does it compare to the number listed in the equation above?
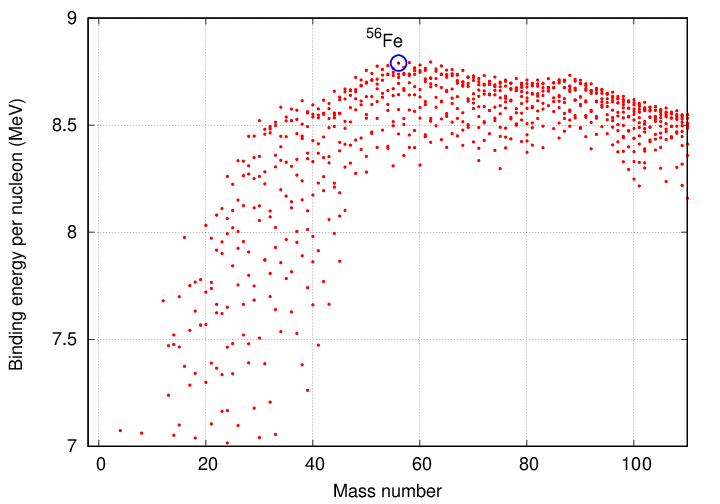
Right. That's a lot of energy. If just a few reactions take place in one section of the white dwarf, it's no big deal -- or is it? Remember, the white dwarf is made of degenerate material, so the density does not change with temperature.
and so a runaway fusion reaction ignites and spreads throughout the star. Simulations of this "flame front" expanding through the white dwarf show some pretty interesting shapes ...

Figures 3 and 4 taken from
Malone et al., ApJ 782, 11 (2014)
Now, as this runaway reaction raises the temperature, even heavier nuclei start to fuse together. Around one billion Kelvin, for example, oxygen starts to fuse into silicon.

Q: As the reactions continue and temperature rises,
will fusion reactions continue to make heavier
elements, all the way to uranium?
No! Look once more at the curve of binding energy. What happens to the binding energy (which is equal to the energy released per fusion) if one tries to combine iron atoms to create a heavier nucleus? The binding energy DECREASES. That means that fusing elements heavier than iron doesn't release energy -- it ABSORBS energy from the environment.

So, this runaway thermonuclear reaction proceeds up to the creation of iron-group elements (including nickel and cobalt), but then slows down. The energy released by all these reactions is large enough to turn the degenerate white dwarf back into ordinary matter, which immediately expands. It expands so fast, in fact, at speeds of over 10,000 km/sec, that the star completely blows apart.
We call the explosion of an entire star a supernova. Believe it not, runaway nuclear reactions inside a white dwarf is NOT the only way to cause a star to explode; there are actually several different varieties of supernova. The version which starts as a white dwarf close to the Chandrasekhar limit is called a "type Ia supernova", or "SN Ia" for short.
A type Ia supernova explosion emits an enormous amount of energy for a few weeks; during that time, it can shine as bright as all the billions of stars in a galaxy, all by itself! The animation below shows one such explosion, which we saw in a relatively nearby spiral galaxy in the year 2011.

Animation courtesy of
The Virtual Telescope Project
After several months pass, most of the energy generated in the reactions has been released into space. All that remains is an expanding cloud of gas, flying outward at thousands of kilometers per second. The gas is often so thin that it is hard to see with optical telescopes -- but it still emits strongly in the X-ray and radio regimes.
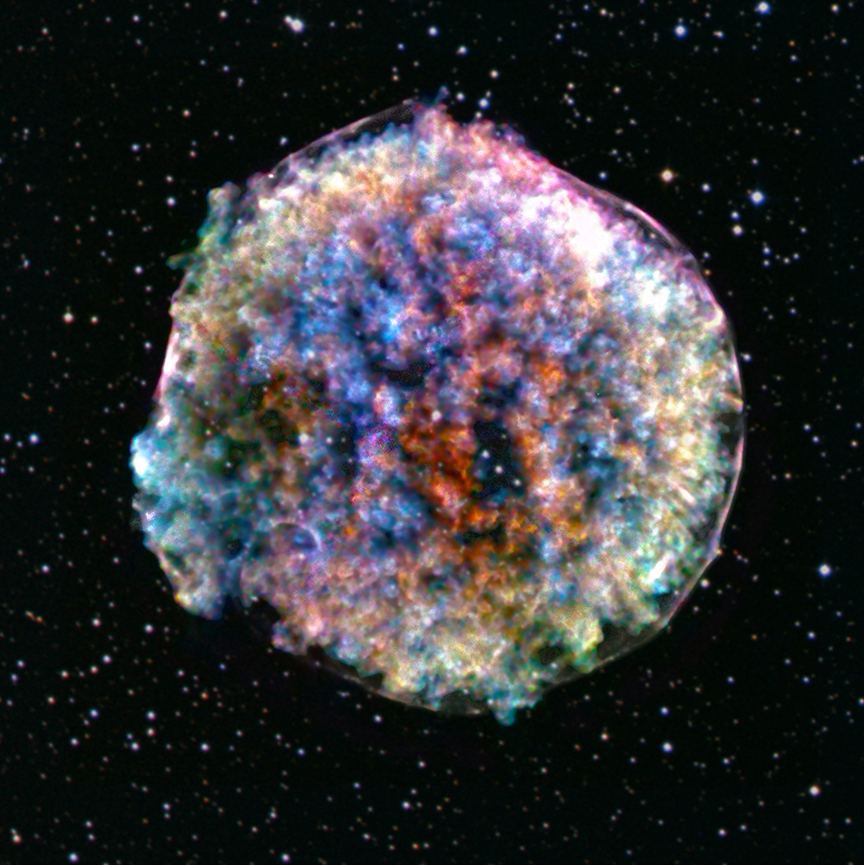
Composite X-ray and optical image of Tycho's supernova courtesy of
X-ray: NASA/CXC/RIKEN & GSFC/T. Sato et al; Optical: DSS
Now, because most of the white dwarfs that explode in this way ought to have very similar properties -- most important, a mass of just under 1.44 solar masses -- we might expect that many of the type Ia supernova explosions ought to have similar properties, too. And that turns out to be true. For example, the light curves of the explosions usually show a very characteristic shape: quick rise and fall in blue, but a slower change in the red, and a second peak in the near-infrared.
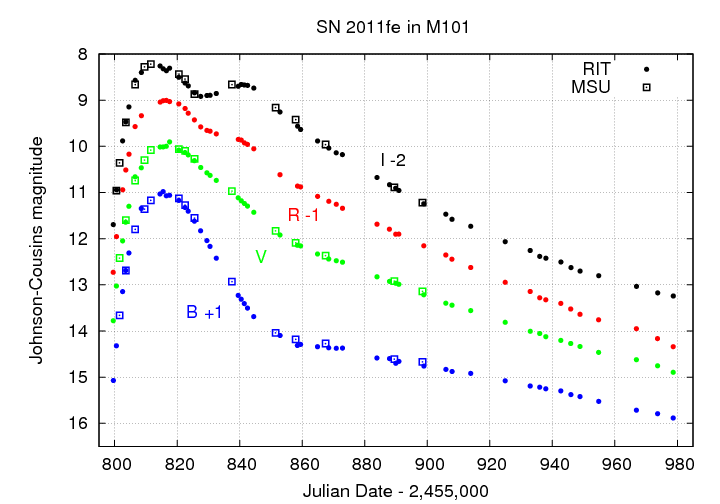
You can
read more about my measurements of SN 2011fe at the RIT Observatory
Astronomers realized that SNe Ia might serve as standard candles: objects which all produce the same luminosity. That means that if one measures the apparent brightness of a type Ia at its maximum light, one can estimate its distance.
In 1991, two groups of astronomers used measurements of a large number of type Ia supernovae to calculate the distances to a set of galaxies; they then compared those distances to the speeds at which the galaxies were moving away from the Milky Way. The combination allowed them to determine the rate at which the universe was expanding, and how that rate has been changing over billions of years. The results were suprising -- and resulted in the Nobel Prize in Physics for three of them.

Announcement of 2011 Nobel Prize in Physics
courtesy of
The Royal Swedish Academy of Sciences
As you can see, white dwarfs can be very useful tools!
At first, high-mass stars -- those with more than about 5 solar masses -- evolve like their low-mass brethren: fusion of hydrogen builds up a core of inert helium, around which a shell of hydrogen-rich material continues to fuse. This causes them to move toward the red-giant portion of the HR diagram.
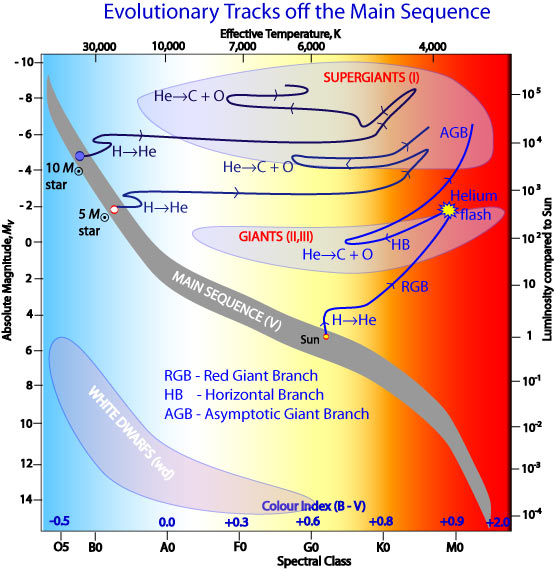
Image courtesy of
CSIRO and Australian National Telescope Facility
Unlike low-mass stars, the cores of high-mass stars do not become degenerate; the temperatures are high enough to maintain a thermal pressure that can support them against gravitational forces.
After the helium core of the star grows dense and hot enough, the triple-alpha fusion reaction begins to convert the helium into carbon. The high-mass star settles into a period of helium-core and hydrogen-shell fusion, just like low-mass stars; it moves back to the hotter side of the HR diagram in this phase.
In fact, the temperatures at the center of a high-mass star are large enough to allow heavier and heavier nuclei to fuse together. As time goes by, the star builds up a series of layers of heavier elements. It also may shift back and forth, from hot to cool on the HR diagram, several times as the fusion rates in its various shells wax and wane. During parts of this journey, conditions in the outer atmosphere may become unstable to radial oscillations; we'll discuss the implications of such oscillating stars another day.

Image courtesy of
CSIRO and Australian National Telescope Facility
Eventually, the interior of the star may look something like this:
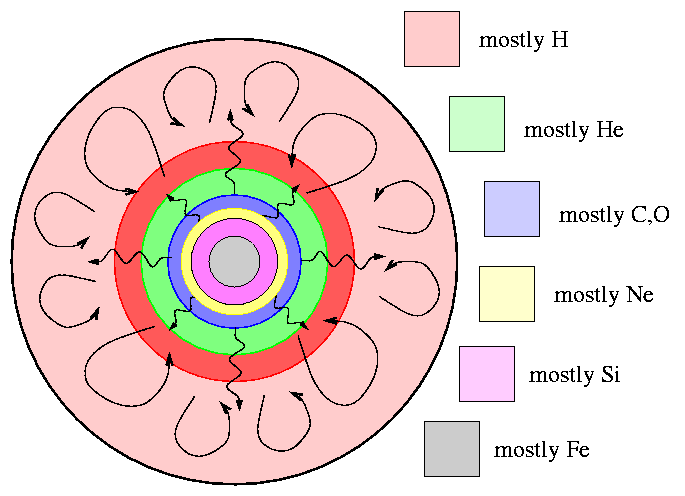
Now, how long does all this take? Not very! In an earlier lecture, we noted that the lifetime of high-mass stars is considerably shorter than that of low-mass stars, because their fusion reactions run at much higher rates. In fact, we found that to a very rough approximation, the lifetime of a star goes like

Q: The lifetime of the Sun is about 10 billion years.
What is the lifetime of a star of 10 solar masses?
What is the lifetime of a star of 20 solar masses?
So, what happens when the star has built up a core of iron? At some point, will the iron nuclei start to fuse together to create heavier nuclei?
NO!
No, iron is the end of the line. Take a look at the curve of binding energy again. Note that iron (and its friends nickel and cobalt) sit at the top of this relationship. The binding energy of nuclei, measured on a per-nucleon basis, starts to DECREASE after iron.

This means that if iron nuclei are fused to create heavier elements, the reaction does not produce energy; it ABSORBS energy. Those reactions cannot produce the thermal energy needed to support the iron core against the pull of gravity. The core of these high-mass stars is typically 1.5-2.5 solar masses -- which means that it exceeds the Chandrasekhar limit. Electron degeneracy pressure cannot support it, either.
So, the core collapses.
It continue to collapse until it reaches a radius of just 10-20 km. At that point, the density is so high that protons and electrons fuse together to form neutrons -- and neutrinos.
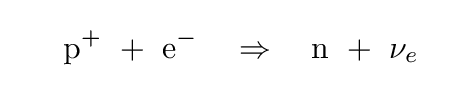
The burst of neutrinos carries a huge amount of energy away from the core of the star. Some of this energy is absorbed by the inner layers of the star, just above the core. In many cases, these layers absorb so much energy and momentum that they are pushed back, outward towards the surface, and given such a high velocity that the entire outer region of the star flies off into space. The star EXPLODES, in what we call a core-collapse or type II supernova.
But many of the neutrinos pass right through the outer layers of the star without interacting at all. They shoot off into space, on a one-way journey to the far reaches of the universe.
Back in 1987, astronomers noticed that one of the stars in the Large Magellanic Cloud, one of the Milky Way's satellites, suddenly increased greatly in brightness and blew off its outer layers. It was the first sign of what came to be known as Supernova 1987A.

Image courtesy of
Roger Groom

Image courtesy of
ESO
Here's a closeup view.


When physicists in Japan and the US checked two large neutrino detectors which just happened to be running at the time, they found a brief burst of neutrinos.

Table taken from
Bionta et al., Phys. Rev. Lett. 58, 1494 (1987)
That was the first --- and last --- time that astronomers detected the neutrino burst from an exploding high-mass star.
So, the outer layers fly off into space, creating a giant cloud of hot, glowing gas, which slowly expands and cools. The animation below shows two pictures of the Crab Nebula (the remnant of a type II supernova which was seen by astronomers in Asia back in 1054), taken in 1973 and 2000.

Credits:
1973 image taken by
Bill Schoening with the 4-m Mayall Telescope at Kitt Peak
on Ektachrome film;
2000 image taken by
Adam Block with the Kitt Peak Visitor Center's 0.4 m telescope
and a CCD camera. Courtesy of
Adam Block,
NOAO and
NSF.
I've measured the light curves of some type II supernova, too. For example, in 1993, a very peculiar core-collapse supernova exploded in the nearby galaxy M82:

Image courtesy of
Lisa Wells
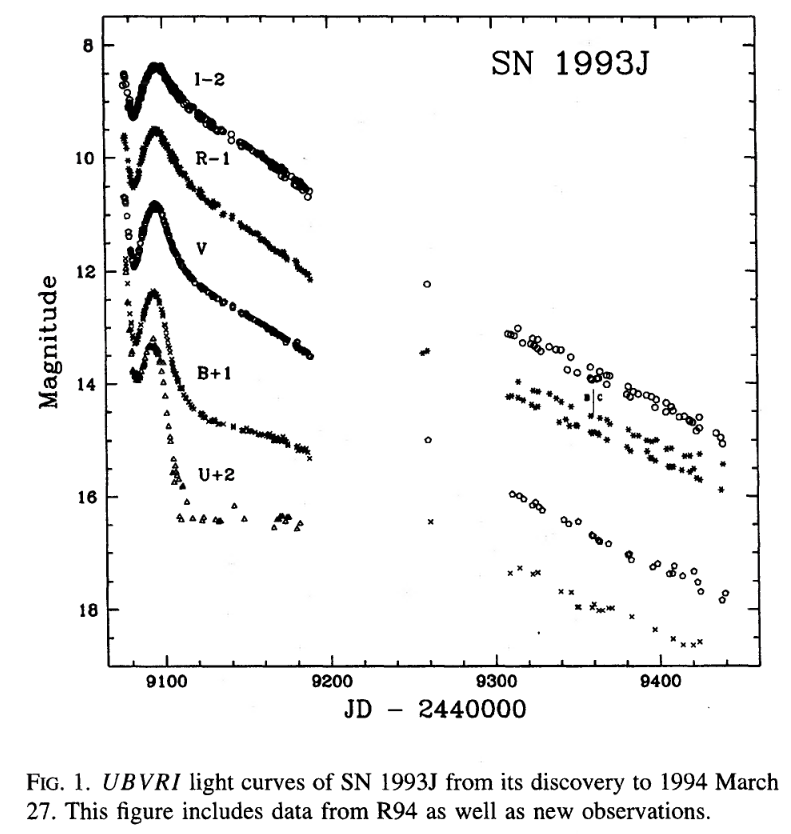
Figure 1 taken from
Richmond et al., AJ, 112, 732 (1996)
More recently, in 2013, a more ordinary type II supernova was discovered in in the spiral galaxy M74.

Image courtesy of Martin Bernier
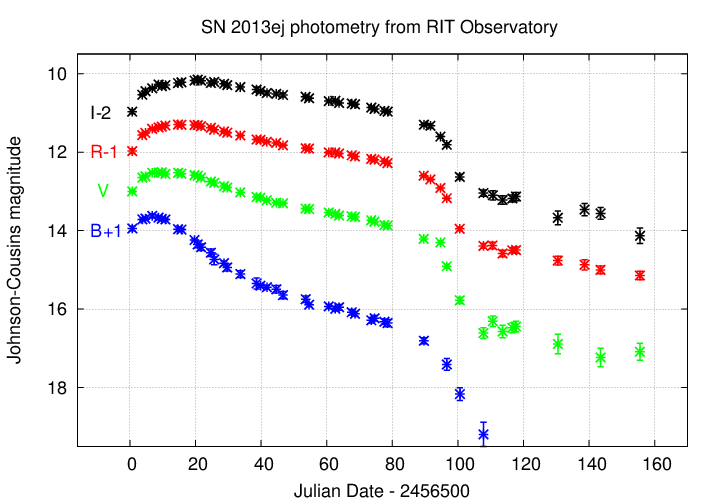
Since stars with a large range of masses, from around 5 or 8 solar masses on the low end to perhaps 20 or 25 solar masses on the high end, can undergo core collapse, there is a large variety in the supernova explosions. It doesn't help that some of a star's outer atmosphere can be removed via gradual mass loss in its later evolutionary stages, leading to a wide range of envelope masses for the explosion to push outward. The bottom line is that one can't treat type II supernovae as standard candles.
However, it turns out that a subset of all core-collapse supernovae -- those which explode inside stars with a very large hydrogen envelope -- may serve as distance indicators of a different sort. By making careful measurements of both the supernova's brightness, and the velocity of its expanding gas, one can deduce the size and temperature of the glowing shell, from which one can estimate the luminosity. This procedure is sometimes called the expanding photosphere method, (or EPM for short). Even though it is far from perfect, it can still give us a rough idea of the distance to an event which may be hundreds of Megaparsecs away.
But, you may be wondering, "what's left at the center of the explosion?" Our story paused as the core of a massive star was crushed inward on itself until it formed a big ball of neutrons. Neutrons, it turns out, belong to the class of particles called "fermions", just as electrons do. That means that they obey the Pauli exclusion principle: no two neutrons may have the same quantum properties. As a result, neutrons, like electrons, resist being compressed due to a quantum mechanical effect called (in this case) neutron degeneracy pressure.
Who will win? Will the degeneracy pressure successfully push back against the inexorable force of gravity, and maintain the core as a tiny sphere of neutronium? Or will the gravitational forces overwhelm all resistance and crush the core down into an infinitesimal point of infinite density? Tune in next time to find out!
 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.