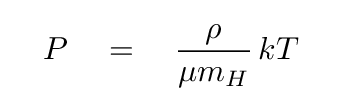
 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
As long as a star can fuse hydrogen into helium in its central core, it will remain on the main sequence. Eventually, however, all that fusion will convert all the hydrogen into helium in the core. What will happen then?
Today, we'll examine the evolution of a low-mass star, similar to the Sun; we'll focus on a few important features of what can be a complex journey across the HR diagram. Next time, we'll follow the life of a high-mass star.
The life of a star on the main sequence is relatively placid. Its luminosity and temperature do change, but only by small amounts, and only over long timescales. The key to this stability is the balance between the weight of the star's outer layers pushing inward on the core, and the thermal pressure of the gas pushing outward. There is a little feedback loop which maintains the system in a state of equilibrium.
Suppose that the rate of fusion reactions in the core DECREASES slightly for some reason. The temperature of the core will drop, and, following the ideal gas law,
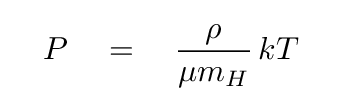
the gas pressure will decrease as well. As a result, the weight of the outer layers will press the core in on itself, causing it to shrink a bit.
However, as the core shrinks, its density must increase. The increase in density leads to an increase in the rate of fusion reactions,
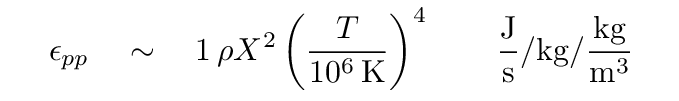
On the other hand, if the fusion rate of the core should INCREASE a little bit, the following sequence will occur:
The connections between the rate of fusion reactions, gas density, pressure and temperature lead the star to regulate itself; any small changes in the central properties will quickly be reversed. One of the key elements in this system is the ideal gas law. What would happen if that should disappear?
Fusion reactions in the core gradually convert hydrogen into helium. At some point, the core becomes so depleted in hydrogen that fusion reactions at the very center cease. The result is an inert core of helium, surrounded by hydrogen-rich material. As the weight of the outer layers presses inward on this inert core, it compresses and shrinks, increasing its temperature. The density and temperature at the outer edges of the core increase as well, reaching values high enough to support hydrogen fusion. A hydrogen-burning shell surrounds the inert core.
(insert diagram here)
In order to keep the core from collapsing, its temperature must be very high. The temperature of the shell surrounding it is likewise very high. As you may recall, the fusion rates of both the proton-proton chain and the CNO cycle are highly sensitive to temperature,
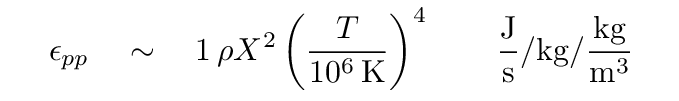
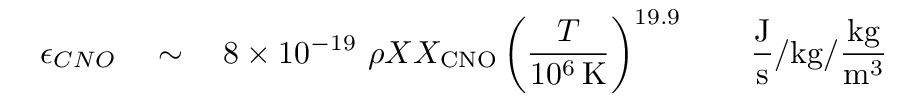
so the total power generated by the hydrogen-burning shell increases far beyond that of the previous hydrogen-burning core. In other words, the luminosity of a star in its hydrogen-shell burning stage is larger than it was on the main sequence. The increased flux pushes the outer layers of the star outward, increasing the surface area and decreasing the temperature of the photosphere. The star moves up and to the right on the HR diagram, moving along the red giant branch.
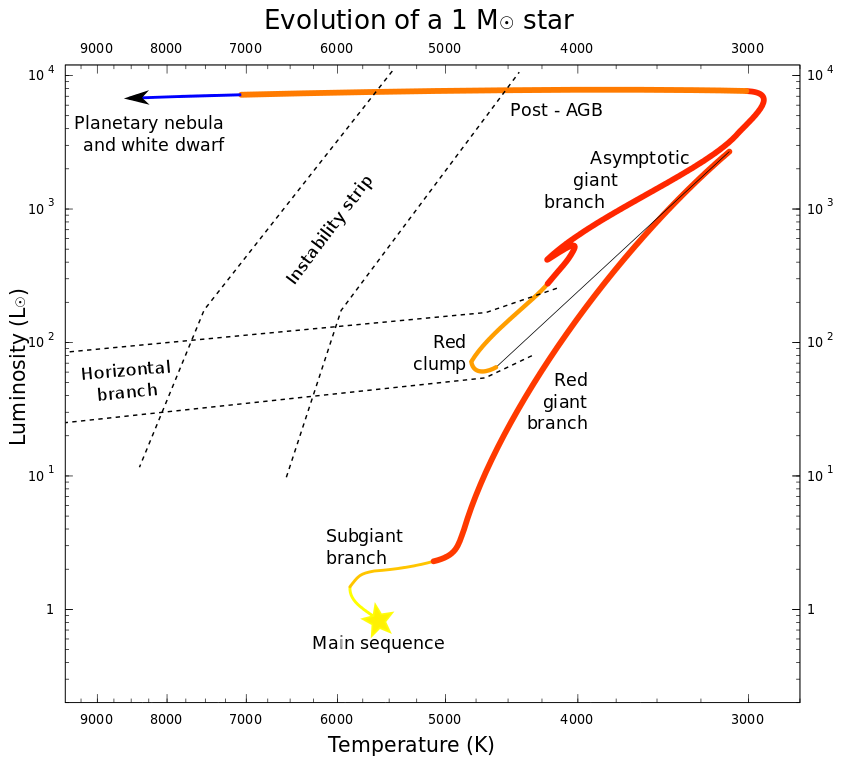
Image courtesy of
Lithopsian and Wikimedia
As hydrogen fuses in the shell, more and more helium is generated, which adds to the mass of the core. The added helium also increases the mean molecular weight of gas in the core. Recall that the mean molecular weight is the average mass of particles in the gas, expressed in terms of the mass of a hydrogen atom. For pure neutral hydrogen, μ = 1. For pure ionized hydrogen, μ = 0.5, since there are two particles (electron and proton) for each hydrogen atom's worth of mass.
Q: What is the mean molecular weight of a pure helium core,
in which all atoms are fully ionized?
Now, the thermal pressure of an ideal gas can be expressed in terms of the mean molecular weight:
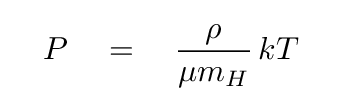
As the core grows rich in helium, its gas pressure decreases; but the overlaying shells and layers of hydrogen-rich material continue to have a smaller value of μ, which means that the pressure they exert on the core remains high. If the difference in the mean molecular weight grows too large, then thermal pressure cannot sustain the core any longer. Back in 1942, Schonberg and Chandrasekhar derived the maximum mass for a thermally-supported core at the center of a star:
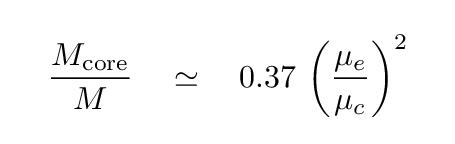
where μe is the mean molecular weight in the envelope, and μc is the mean molecular weight in the core.
Q: Using a value of μe = 0.61 (appropriate for
a hydrogen-rich envelope) and the value of μc
you calculated earlier, what is the critical mass for a helium
core?
That sounds like trouble. If thermal pressure can't support the core against the pressure of the outer layers .... what happens?
The first thing is obvious: the core collapses, shrinking relatively quickly. But long before it disappears, a new physical mechanism appears to provide the support it needs: electron degeneracy. This is quantum mechanical effect, based on the Pauli exclusion principle. Since the electrons moving freely in the ionized helium core are fermions, they cannot occupy the same quantum state as any other electron. For our purposes, the result is simply that a new type of pressure appears when the density reaches a (very high) threshold, and prevents the core from collapsing any further.
How high must the density rise for degeneracy to become important? For a star of one solar mass, the density must increase by roughly a factor of 30,000!
Q: One teaspoon contains a volume of 5 ml = 5 x 10-6 cubic meters.
One elephant has a mass of M = 5 tonnes = 5000 kg.
How many elephants does it take to equal the mass of a single
teaspoon of degenerate matter?
So the core of the star turns into degenerate matter -- it's superdense now, which is sort of cool, but you might be thinking, "What's the big deal?"
The big deal is that the equation of state for degenerate matter is NOT like that of ordinary matter. Ordinary gas follows the ideal gas law: the pressure and density of the material are connected to the temperature.
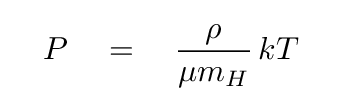
But the equation of state for degenerate matter looks different, something like this, in which K is just some constant.
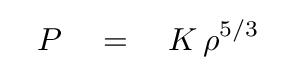
No connection to temperture! If the temperature of this degenerate core rises ... it won't expand, or push outward. It will just heat up.
That becomes key as the star continues to rise up along the red giant branch. As it rises, the shell burning hydrogen produces more and more helium, which moves into the core, increasing its size and mass. The pressure on the core increases, and its density increases. The temperature of the neighboring hydrogen-burning shell increases, too. At some point, the helium core reaches a density and temperature at which the triple-alpha process starts to fuse helium into carbon. This reaction (as you may recall) is VERY sensitive to temperature:
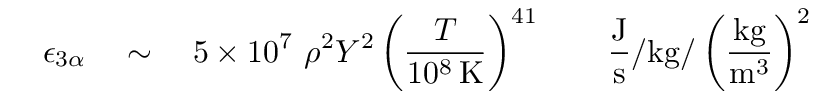
So, when the reactions begin, they produce energy, which raises the temperature of the helium core.
Q: How does the core respond to an increase in temperature?
That's right -- it does NOTHING. It just sits there, keeping the same size and density. So, the temperature rises, which increases the rate of fusion, which creates more energy, which increases the temperature, which increases the rate of fusion ... etc. It's a runaway positive feedback reaction.
BOOM!
This sudden burst of helium fusion is called the helium core flash. It can produce a HUGE amount of energy, as much as the star normally produces in thousands of years, but all in a few seconds or minutes.
Strangely enough, it does not produce a large observable "kaboom", or flash of light. Most of the energy produced by the flash is used up in converting the degenerate core back into non-degenerate, ordinary matter. The remainder may push the outer envelope out briefly, but the star remains in one piece, and soon settles down.
There IS one observable consequence, however: now that helium fusion has started in the core, the star slides back down the red giant branch in the HR diagram and settles down in a new location. It will remain here for a relatively long stretch of time, since it now has a new, relatively large source of fuel: helium.
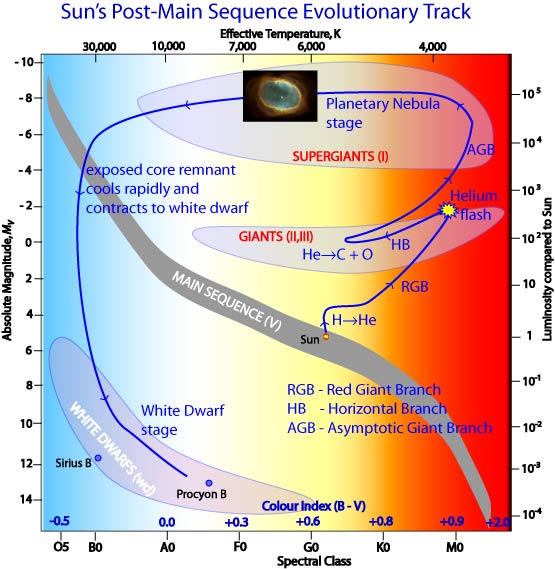
Image courtesy of
CSIRO/Australia National Telescope Facility
The area of the HR diagram occupied by stars in their "fusing helium to carbon in their core" phase covers a roughly horizontal span, which has two common names:
You can see the "red clump" in this diagram from the Gaia DR2 database,
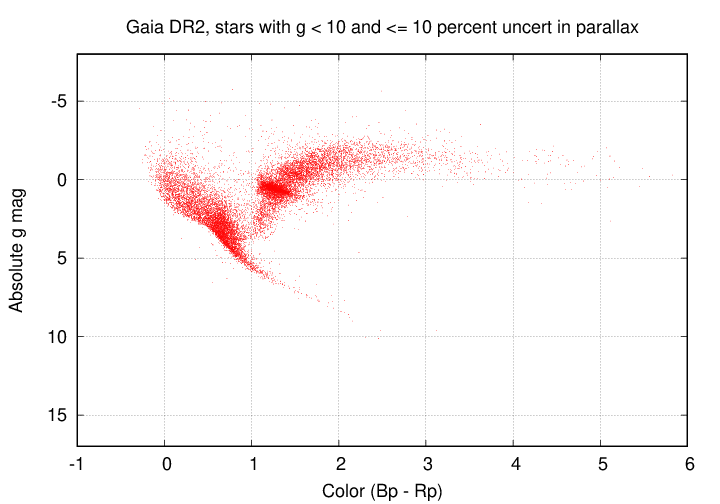
and the "horizontal branch" in this dataset, which consists of stars in several globular clusters. Note that the location of a star on the horizontal branch depends on its metallicity: stars with low metallicities (almost pure H/He) have blue colors and high photospheric temperatures, while those enriched with heavier elements have reddish colors.
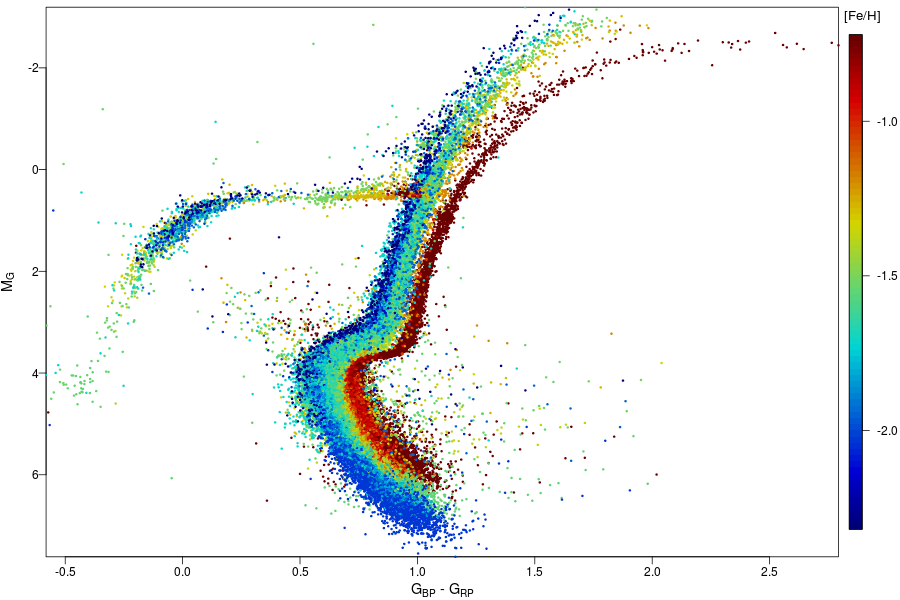
Image courtesy of
ESA/Gaia/DPAC, Carine Babusiaux
and co-authors of the paper
"Gaia Data Release 2: Observational Hertzsprung-Russell diagrams(link is external)".
The lifetime of a star in this stage of its life, fusing helium to carbon in its core, is relatively long .... but not as long as the stage when it fused hydrogen into helium. To a rough approximation, stars spend about 10% of their main-sequence lifetimes in this core-helium-fusing stage. For the Sun, this means about 1 billion years.
What happens next? Things get complicated, depending strongly on the initial mass of the star, and the timescales grow shorter, so I'll just provide a brief outline of some of the major events.
Fusing helium into carbon produces a lot of carbon, as well as quite a bit of oxygen. So, at the center of the star, a new inert core begins to appear. This one is composed of carbon and oxygen, and is surrounded by a helium-burning shell. Above that is a zone of helium, on top of which sits a hydrogen-burning shell. Perched at the very top of the star is a large envelope of hydrogen and helium. The star resembles some sort of fancy European pastry dessert.
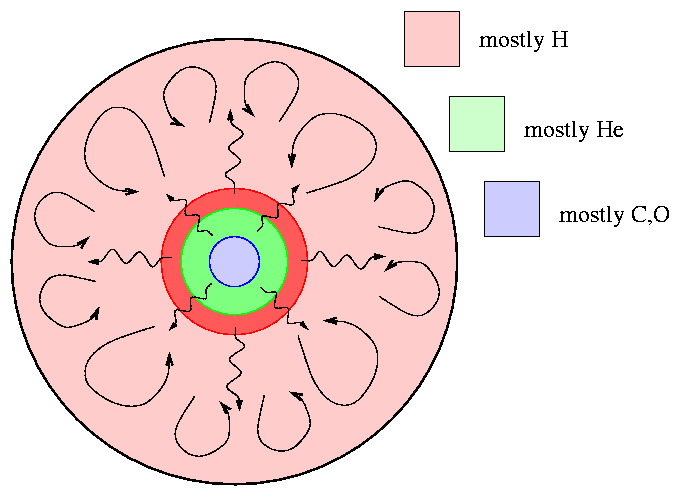
As the inert core grows, the helium- and hydrogen-burning shells must produce more and more energy in order to keep the thermal pressure high enough to balance the graviational forces pulling everything in. The star again climbs upward on the HR diagram, this time along the asymptotic giant branch (ABG). It's nearly parallel to the red giant branch, just a bit to the left.
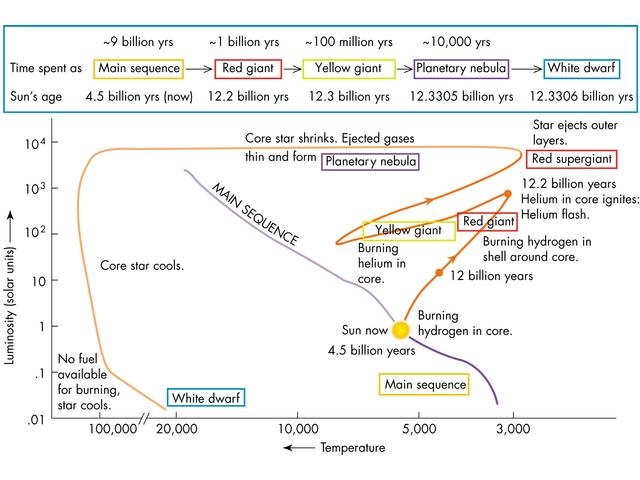
Image courtesy of
The Sloan Digital Sky Survey
What happens next? For rather complex reasons, both the hydrogen-burning shell and the helium-burning shell suffer from instabilities: the fusion rates can slow down to a halt, then start up again later if the temperatures and densities reach critical thresholds. The layer of helium just above the carbon-oxygen core can become partially degenerate, which means that shell helium flashes can occur. These violent re-startings of helium fusion can release a large amount of energy all of a sudden, which can push the outer layers of the star outward for a brief period.
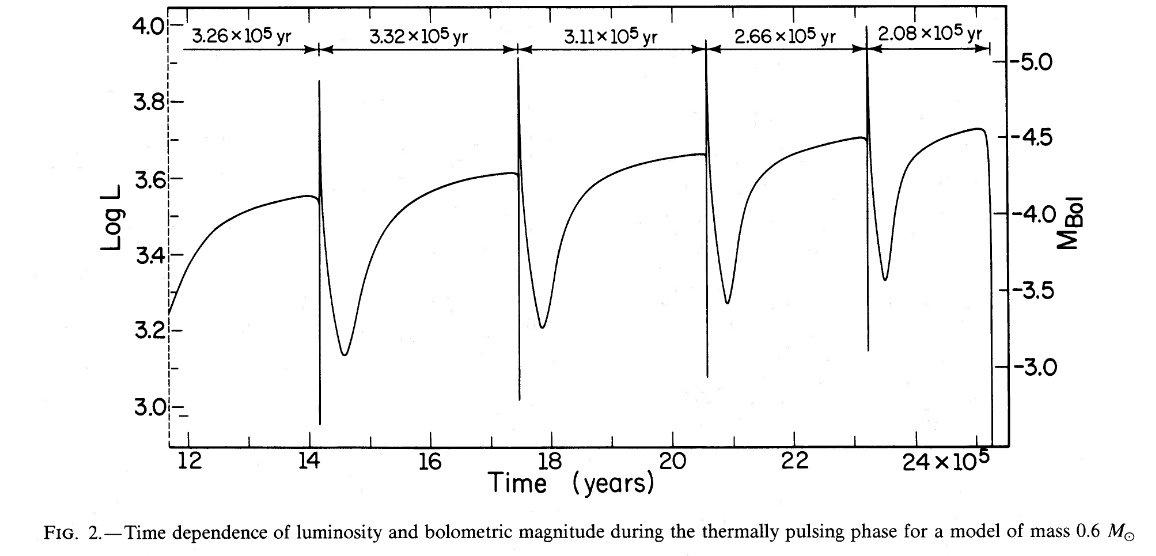
Figure 2 taken from
Iben, ApJ 260, 821 (1982)
At some point, or at multiple points, gas in the outer envelope of the star is pushed off into space. This episode(s) of mass loss can liberate a small fraction of the star's initial mass into expanding shells of gas which waft outward, never to return.
What's left behind? The compact and VERY HOT inner layers of the star, now uncovered and exposed directly to the universe. What does the universe see? A very luminous, very hot, rather small, object.
As the outer layers are gently pushed off the star, uncovering the hot core, the star slides to the left in the HR diagram.

Image courtesy of
The Sloan Digital Sky Survey
In an intriguing little sidenote, these episodes of mass loss during the late stages of its evolution may turn out to be crucial for the future of the Earth. You can read more about this story in the article mentioned at the end of this webpage.
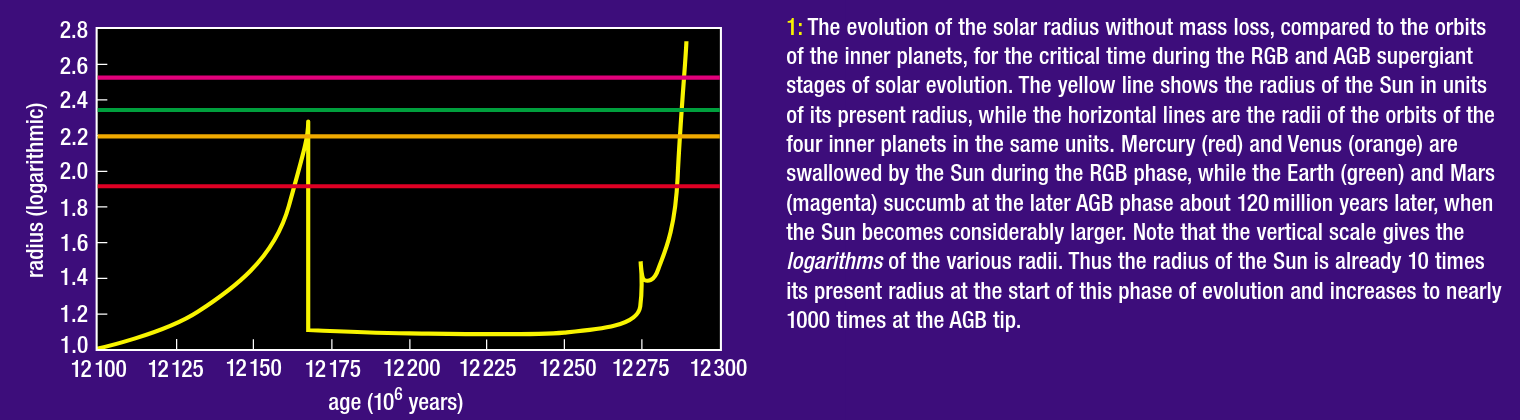
Figure 1 taken from
Solar evolution and the distant future of Earth ,
by Schroder, Smith and Apps (Astronomy and Geophysics,
vol 42, p. 6.29 (2001)).
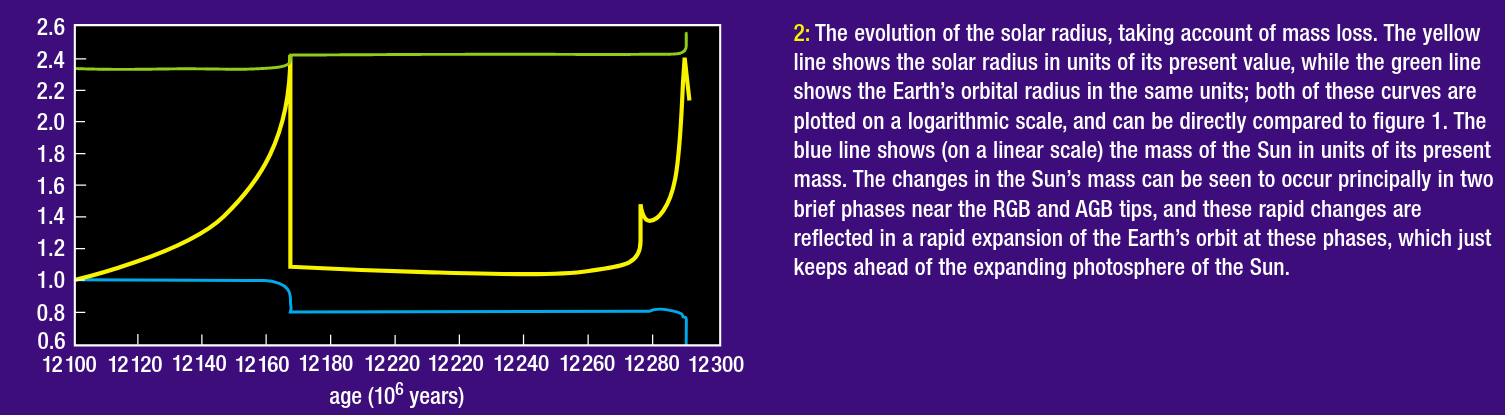
Figure 2 taken from
Solar evolution and the distant future of Earth ,
by Schroder, Smith and Apps (Astronomy and Geophysics,
vol 42, p. 6.29 (2001)).
What happens next? For low-mass stars, with initial masses of less than 2 or 3 solar masses, not much. The density and temperature at the center of the star never rise high enough to ignite the carbon-oxygen core. As the outer layer disappear, the pressure on the hydrogen- and helium-burning shells decreases, which lowers their densities and temperatures. Fusion halts. The star -- gradually -- cools down.
The end result will be a white dwarf: the carbon-oxygen core of the original star, basically, usually covered with very thin layers of helium and, at the very top, hydrogen.
You can see some of the stars in these last phases of their evolution in the HR diagram below. Eventually, they will slide down to the lower-left corner, where all the white dwarfs hang out.
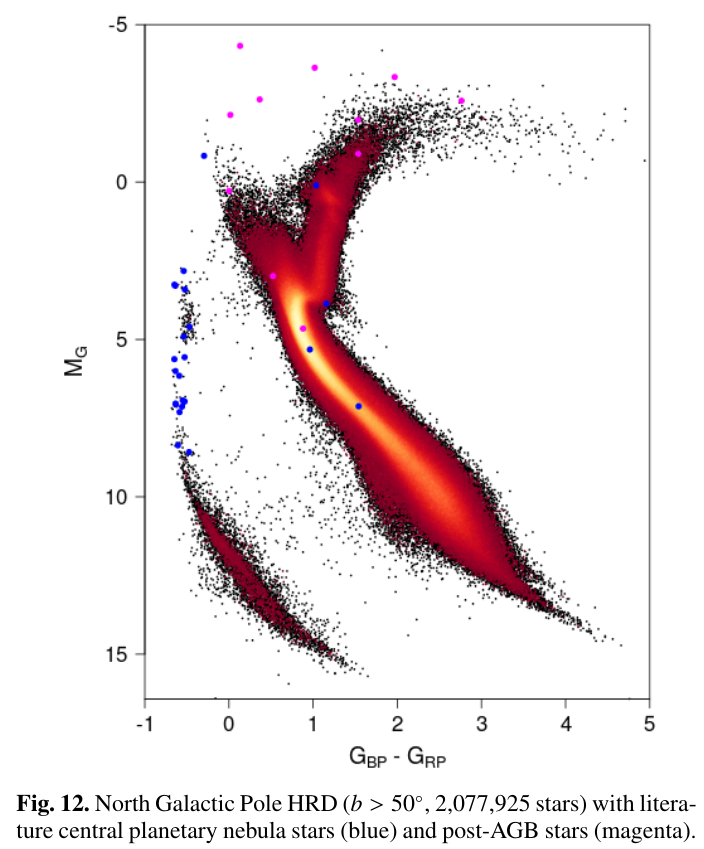
Figure 12 taken from
ESA/Gaia/DPAC, Carine Babusiaux
and co-authors of the paper
"Gaia Data Release 2: Observational Hertzsprung-Russell diagrams(link is external)".
White dwarfs are common, but hard to find. The problem is that they are just so SMALL! Even though they tend to have high temperatures, their very small surface area means that they don't emit a great deal of radiation. The picture below shows the nearby binary star system consisting of

Image Image courtesy of
NASA, ESA, H. Bond (STScI) and M. Barstow (University of Leicester)
Q: A typical white dwarf is the size of the Earth (R = 6370 km)
and has a temperature of T = 10,000 K.
Assume that it emits like a blackbody
(and recall that σ = 5.67 x 10-8 W/m^2 K^4)
What is the luminosity of such a star?
How does it compare to the luminosity of the Sun (L = 3.8 x 1026 W)?
Occasionally, when we look at a star which has evolved past the red-giant stage, we catch it just as it starts to move across the HR diagram, while it is still surrounded by the shells of gas that were blown off its outer atmosphere. The very hot proto-white-dwarf at the center floods the region with ultraviolet radiation. All those ultraviolet photons run into thin shells of gas.
Q: What happens when thin clouds of gas are excited by
lots of optical and ultraviolet photons?
This is what happens!
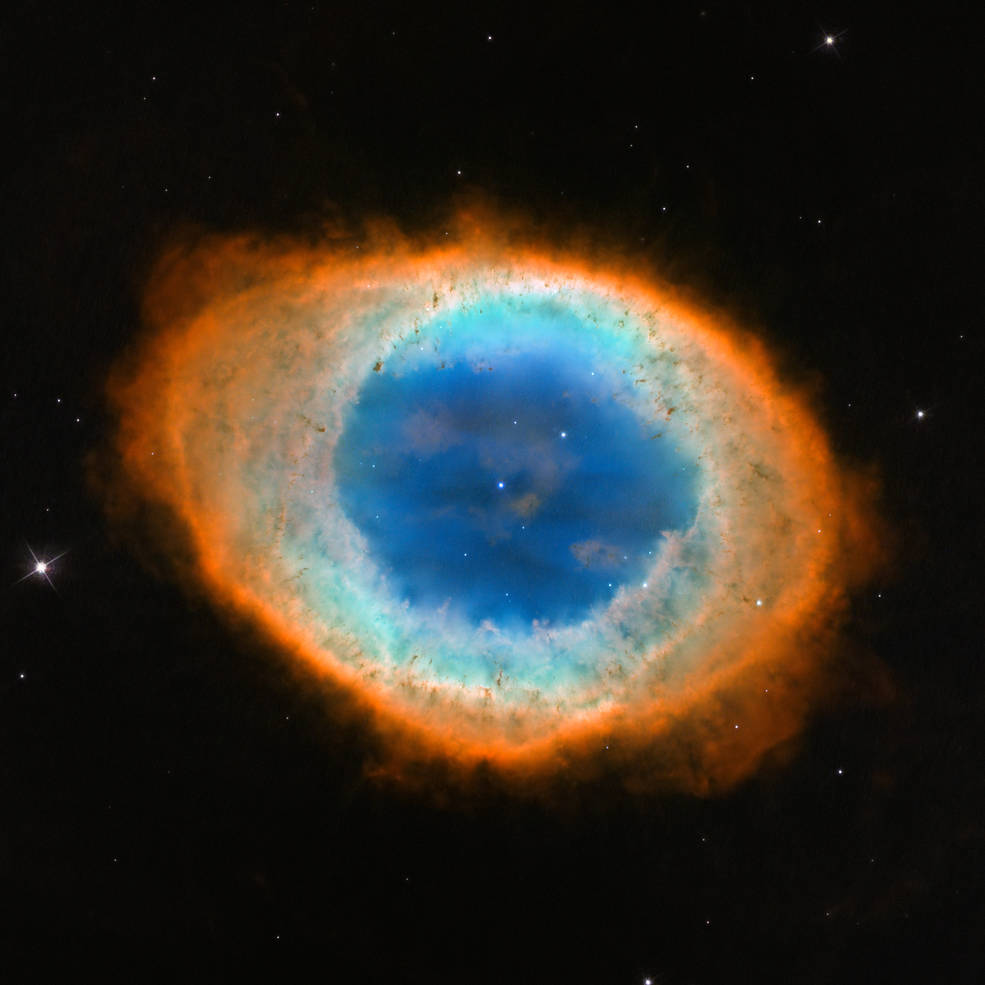
Image of M57, the Ring Nebula, courtesy of
NASA, ESA and the Hubble Heritage (STScI/AURA)-ESA/Hubble Collaboration
Absorbing the UV photons ionizes and/or excites the atoms. As the atoms drop back down to lower energy levels, they emit photons with energies corresponding to the differences in their energy levels. In other words, the gas produces an emission-line spectrum.
To human eyes, the results can be very pretty ... and also informative. The shapes of the clouds in these pictures can tell us about the details of the mass loss process. In many cases, the bilateral symmetry suggests that the star is one member of a binary system.

Images of planetary nebulae showing X-rays (purple)
and optical (red, green, blue) courtesy of
X-ray: NASA/CXC/RIT/J.Kastner et al.; Optical: NASA/STScI
 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.