 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
When the fuel runs out near the center of a massive star, its core collapses. One possibility -- if the core contains no more than about 2 or 2.5 solar masses -- is that the collapse will halt when neutron degeneracy pressure forms a neutron star. But if the core exceeds that mass, even neutron degeneracy pressure can't stop it from continuing to shrink. It will become a peculiar object that we call a black hole.
As you may recall, the degeneracy pressure due to electrons can stabilize the helium or carbon/oxygen core of a star -- as long as that core contains less than about 1.4 solar masses. That pressure occurs because electrons are members of a class of sub-atomic particles called "fermions", which resist having the same quantum properties as other particles.
As you may also recall, neutrons are ALSO fermions, and so they, too, exhibit a degeneracy pressure when forced into very close proximity to other neutrons. During the collapse of the iron core of a massive star, electron degeneracy pressure is insufficient to halt the compression ... but, in some cases, neutron degeneracy pressure can stop it. The upper limit isn't known precisely, but neutron stars may form as long as the core is less than about 2.5 solar masses.
But if the core contains MORE mass, then even neutron degeneracy pressure is overwhelmed by the force of gravity and the pressure of the overlying layers of material. The core will continue to collapse, and, as far as we know, never stop. It will shrink down to an infinitesimal point, a region of infinite density; a place where the laws of physics might break down. In other words, the core might become a singularity.
For our purposes, all we need to know is that this bizarre, tiny object is covered by a sort of cloak, called an event horizon. Within the event horizon, very strange things might happen -- but we have no way of finding out. The event horizon marks the last point at which we can detect matter and radiation before it disappears into the black hole.
From our point of view, black holes are pretty simple. Because we can't see inside the event horizon, we know nothing of the internal structure(s) that might exist. All that we can detect is based on three properties of the black hole which have measureable effects on the outside world:
If a black hole happened to gain an electric charge -- by engulfing more electrons than protons, for example -- then under most reasonable circumstances, electric forces would attract positive charges to fall in and neutralize it in short order. We'll therefore ignore the effects of electric charge on a black hole.
The effects of angular momentum can be very important, as a number of studies have shown. A spinning black hole can modify the nature of the space around it, leading to a number of observable consequences: a change in the size and shape of the event horizon, for example, or instabilities in the orbits of objects just outside the event horizon. Astronomers who study black holes must indeed account for the angular momentum of their subjects. We, however, will ignore it. If you want to learn more about the details from real experts, visit
For us, however, the nature of a black hole depends solely on its mass. Let's see what consequences that one property can have.
I've swept all the interesting parts of a black hole under a metaphorical rug called the "event horizon". Well, just how big is this horizon? How does the size of this region depend on the mass of the black hole?
In order to answer this question, let's take a step back to a simpler system: an ordinary sphere of ordinary matter, such as the Earth.
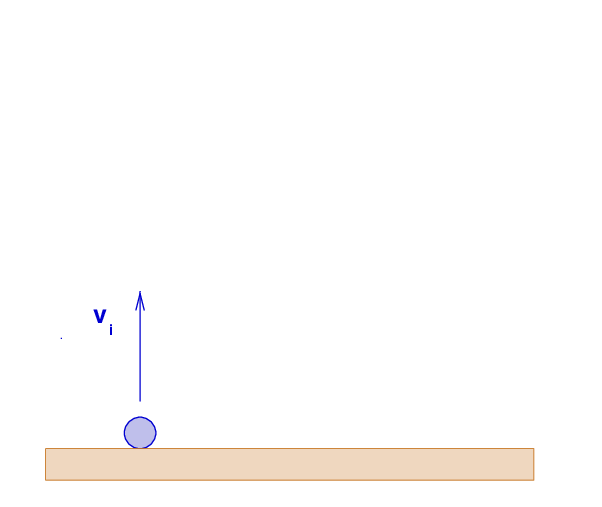
Q: What happens if one tosses a ball straight up into the air?
Right. It rises upward for a short time, but slows as it rises. Eventually, it stops moving away from the surface of the Earth, pauses momentarily, and then falls back to the ground.

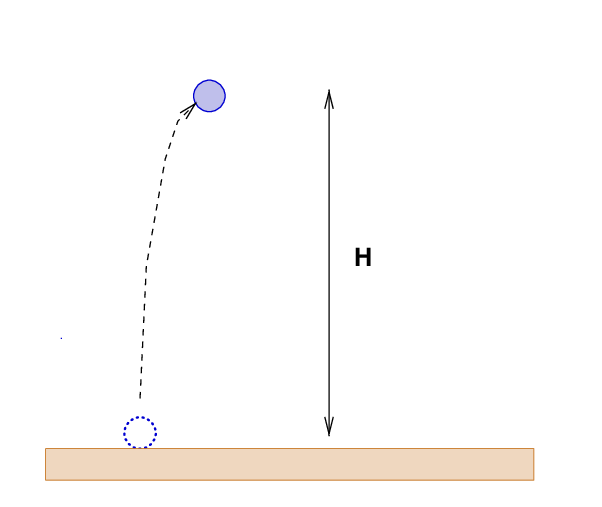
Q: What is the relationship between the initial velocity vi
of the ball, and the maximum height H of its trajectory?
Right again. The key is to use the conservation of energy at two moments: when the ball is tossed up from the ground, and when it reaches the peak of its motion.
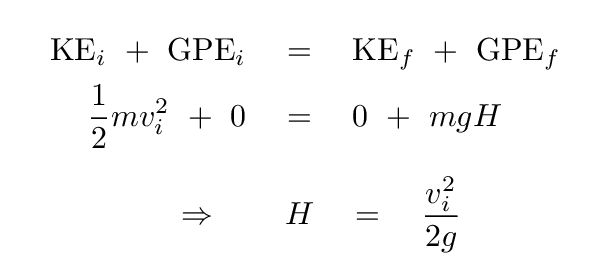
Suppose that instead of tossing a ball up by hand, we loaded the ball into a cannon. A big cannon. A VERY big cannon.

Illustration by Henri de Montaut
from Jules Verne's book From the Earth to the Moon.
In this case, the ball would rise so high that the Earth's gravitational force would change; instead of using a constant force mg, we would have to compute the force -- and potential energy -- at each moment using the Universal Law of Gravitation. That means that our equation for conservation of energy would change a bit. If the ball starts at a distance Ri from the center of the Earth, and halts when it reaches a distance Rf, then the equation becomes
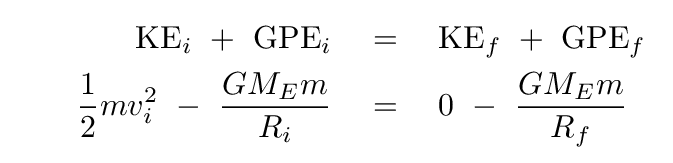
Suppose that we shoot the ball up with JUST the initial velocity needed to keep it moving up and up and up forever -- so that it keeps slowing down, but so slowly that it only stops when it reaches an infinite distance away from the Earth. In other words, suppose that the final distance is Rf = ∞. Moreover, suppose that we shoot the ball from the surface of the Earth; that means that the initial distance Ri = RE, the radius of the Earth. In this very special case, our equation becomes

Q: Can you solve for the initial velocity which will cause
the ball to stop only when it has reached an infinite distance?
Very good.
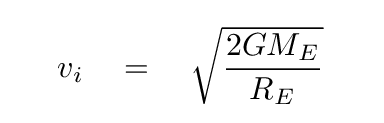
We can use the same reasoning to derive this special speed, called the escape velocity, which will send an object infinitely far away from a spherical body of mass M and radius R.
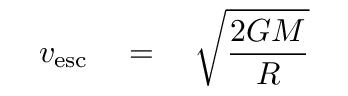
"That's all very nice," you might be thinking, "but weren't we talking about black holes?" Yes, we were. It turns out that the escape velocity from a black hole is so fast that nothing, not even light, can leave it. In other words, the escape velocity from a black hole's event horizon is vesc = c. And that allows us to derive the radius of the event horizon around a black hole of mass M.

Q: What is the radius of a black hole with a mass equal to the Sun?
(M = 1.99 x 1030 kg)
Q: What is the radius of a black hole with a mass equal to the Earth?
(M = 5.98 x 1024 kg)
But -- wait a minute. If the gravity of a black hole is so strong that not even light can escape from it, then what will be SEE if we look at a black hole?

Nothing.
"If we can't SEE the black hole," you are probably shouting at this point, "then how do we know that it exists?"
That's a good question. We must turn to INDIRECT evidence if we wish to infer the presence of a black hole. Fortunately, nature has provided several situations in which astronomers can be pretty sure that we have, indeed, found one.
One of those situations involves a binary system in which a star orbits around a companion of some sort. In many cases, that companion is another star. Sirius is an example of this sort of system.

Image of Sirius A and Sirius B courtesy of
NASA/ESA/H. Bond (STScI) and M. Barstow (Univ. Leicester)
As astronomers have watched over many decades, the two stars have moved relative to each other. Using Kepler's Third Law, we can derive the masses of the two stars (which turn out to be roughly 2 solar masses for Sirius A, and 1 solar mass for Sirius B). Everything checks out.

Image courtesy of
Burnham's Celestial Handbook, 1978, v1, Robert Burnham, Jr.)
But in a few cases, astronomers noticed that something didn't add up. In a system called "Cygnus X-1", for example, a hot, massive star was clearly orbiting around a second object.
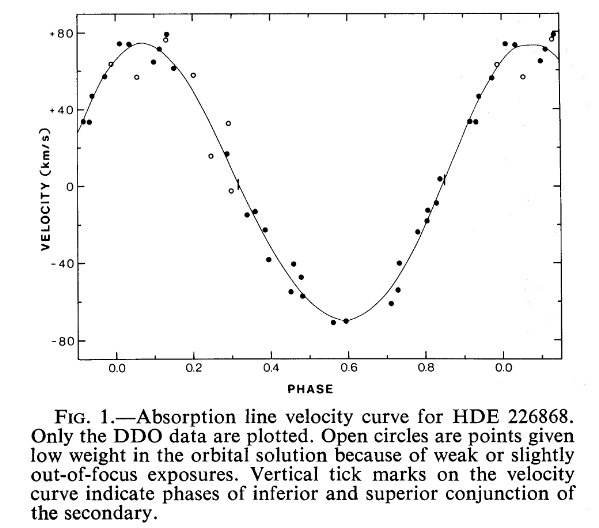
Figure 1 taken from
Bolton, ApJ 200, 269 (1975)
The visible star was clearly massive. Based on the properties of the orbit, scientists could estimate the mass of its companion. The pink area below shows an early estimate of the masses of the two stars: the visible star's mass, M1, appears on the horizontal axis, while the invisible object's mass, M2, appears on the vertical axis. There is quite a bit of uncertainty, but even the minimum value of the companion's mass is far above the limit for a neutron star.
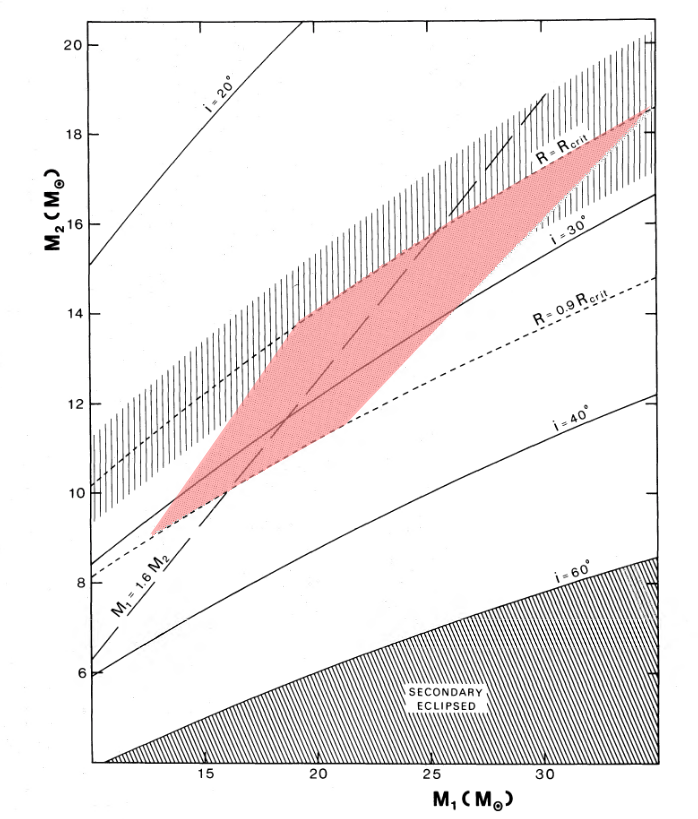
Figure 2 taken (and modified) from
Bolton, ApJ 200, 269 (1975)
But no matter how hard they looked, astronomers could not find evidence for light from a second ordinary star in this system. Any main sequence star of 8 or 10 solar masses would emit enough light to be detected easily ... yet it wasn't there.

Abstract of
Mauder, A&A 28, 473 (1973)
A more recent example of this type of evidence comes from the center of our Milky Way Galaxy. Surrounding the center is a loose cluster of stars which shine brightly in the infrared. With very careful work, a team of astronomers has measured the positions of these stars over and over again for the past twenty-three years. Click on the image below to play a movie showing these motions.
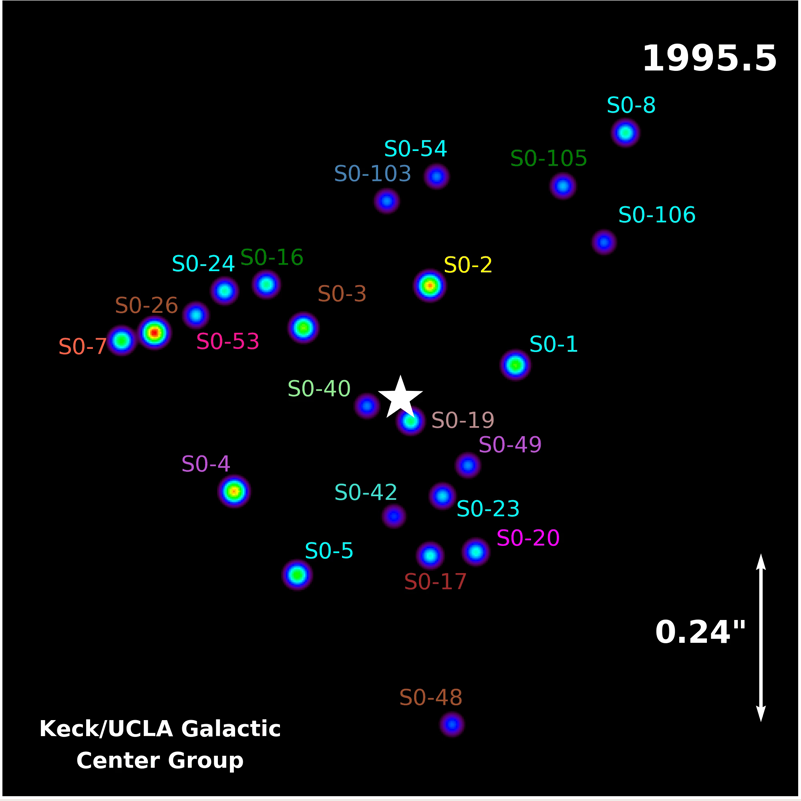
Movie courtesy of
The UCLA Galactic Center Group
Applying Kepler's Third Law to these orbits, the UCLA Galactic Center Group has been able to estimate that there is an object at the center of the Milky Way (at the location marked with the white star in the figure above) which must have a mass of about 4 MILLION solar masses. That's not an ordinary black hole formed by the collapse of a single star, but a more complicated beast with a long history. Nonetheless, the fact that it has so much mass and yet emits no appreciable energy itself is a very strong argument that it must be a black hole.
These observations of the Milky Way's center, by the way, are so impressive, and so strong a piece of evidence for the existence of black holes, that two of the team were awarded the Nobel Prize in Physics this year.

Image courtesy of
The Royal Swedish Academy of Sciences
There is another way astronomers can find black holes, even if they can't see them directly. In many situations, a black hole may be surrounded by gas or other material. For example, the black hole may be one member of a binary system, like Cygnus X-1, in which the other object is an ordinary main-sequence star. In that case, some of the gas in the outer atmosphere of the stellar companion, which is held onto the star only loosely by gravity, may be peeled off and pulled toward the black hole.
As it approaches the black hole, the gas cannot simply fall directly into the event horizon due to its angular momentum. Instead, it forms a flattened accretion disk surrounding the hole.

Artist's rendition of Cygnus X-1 courtesy of
NASA, ESA, Martin Kornmesser (ESA/Hubble)
A single, isolated atom of gas would settle into an elliptical orbit of some size and remain in it for a very long time -- just as the Earth circles the Sun in a stable orbit. However, because the gas consists of many different atoms, each with a slightly different angular momentum around the black hole, the atoms collide with each other as they all swirl around. Those collisions cause several things to happen:
Over time, individual particles of gas move from the outer regions of the accretion disk to the inner regions.
Q: What happens to the gravitational potential energy (GPE)
of a particle if its orbit decreases in size?
Yes, that's right: as the radius of its orbit shrinks, the GPE of a particle decreases. Remember,
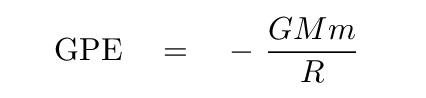
Where does all this GPE go? Some of it goes into kinetic energy -- the gas particles near the center move faster than those in the outer regions of the disk. But some of it also is radiated away as optical, infrared, radio, UV, and X-ray photons. In one sense, a black hole is a machine which converts matter (infalling gas) into energy (radiated photons). In fact, some people have suggested using black holes as power stations.

Plan courtesy of
Yonatan Zunger
The efficiency of a black hole in converting matter into energy is pretty darn high. For example, Bian and Zhao, PASJ 55, 599 (2003) estimate that between 2 and 10 percent of the rest-mass energy (mc2) of a cloud of gas might be radiated away by the time the gas finally penetrates the event horizon. If you go back to our discussion of hydrogen fusion in the Sun, you will find the fusion has a lower efficiency: only about 0.7 percent of the rest-mass of the gas is turned into energy.
Q: In a future advanced civilization, Fred tosses an apple core,
of mass 0.010 kg, into his Hole-A-Way garbage
disposal unit. The apple core is sent into an accretion
disk around a black hole, and 3 percent of its mass is
converted to energy. How many Joules are released?
Compare that to the amount of energy required to run the RIT
campus for one year: about 6 x 1014 J
(see https://www.rit.edu/sustainablecampus/energy).
How can we recognize an accretion disk? Well, it should consist of gas which spans a very wide range of temperatures: cool (hundreds of Kelvin) in the outer regions, warm (tens of thousands of Kelvin) in the middle, and hot (millions of Kelvins) near the black hole.
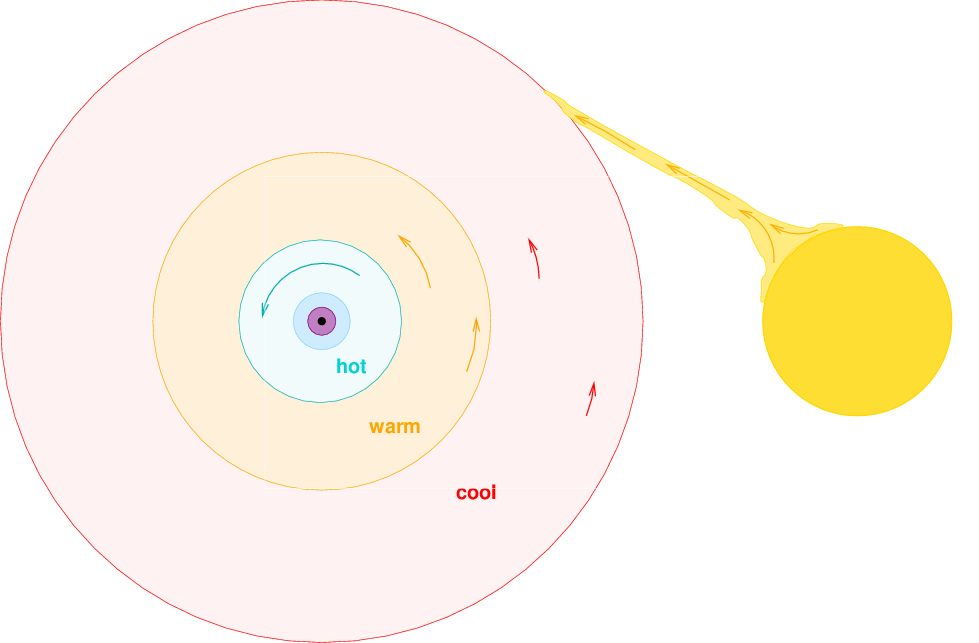
The gas will therefore emit blackbody radiation with different peak wavelengths in different regions.

So, we should see photons over a very broad range of wavelengths (or energies, or frequencies) coming from an accretion disk. As we do for many sources, such as Markarian 421.
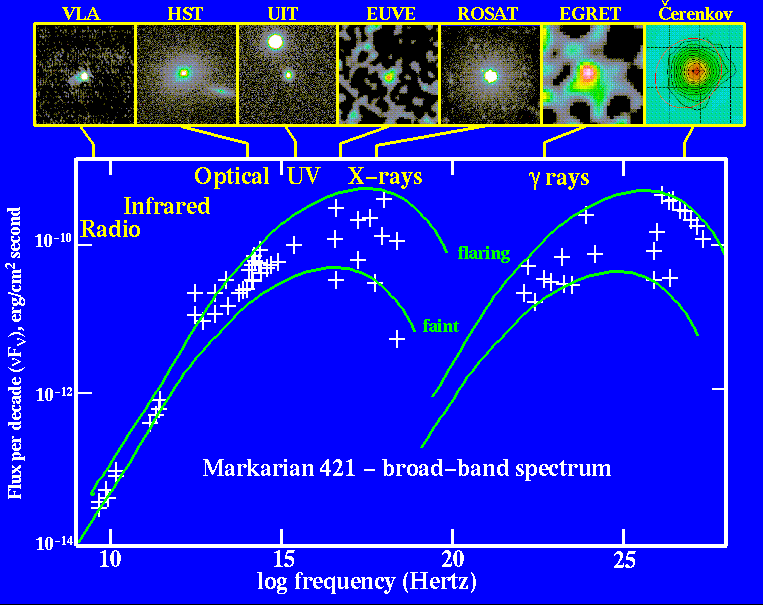
Image courtesy of
Bill Keel
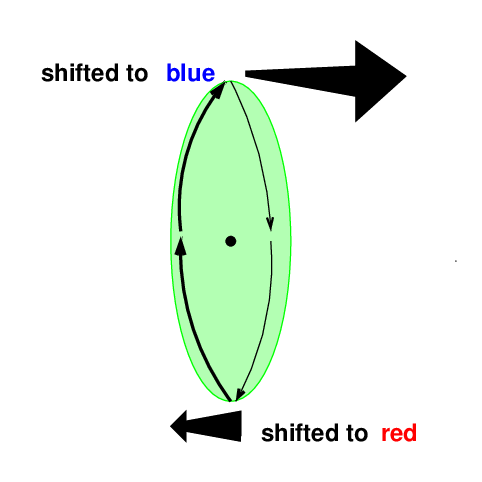
In addition, the gas in the accretion disk moves around the black hole at the center, with speeds that increase toward the center. If one particular disk happens to be oriented roughly edge-on to our point of view, then on one side, the gas will move toward us, while on the other side, the gas will move away from us. That means that we should see both redshifted and blueshifted gas when we look at an accretion disk.
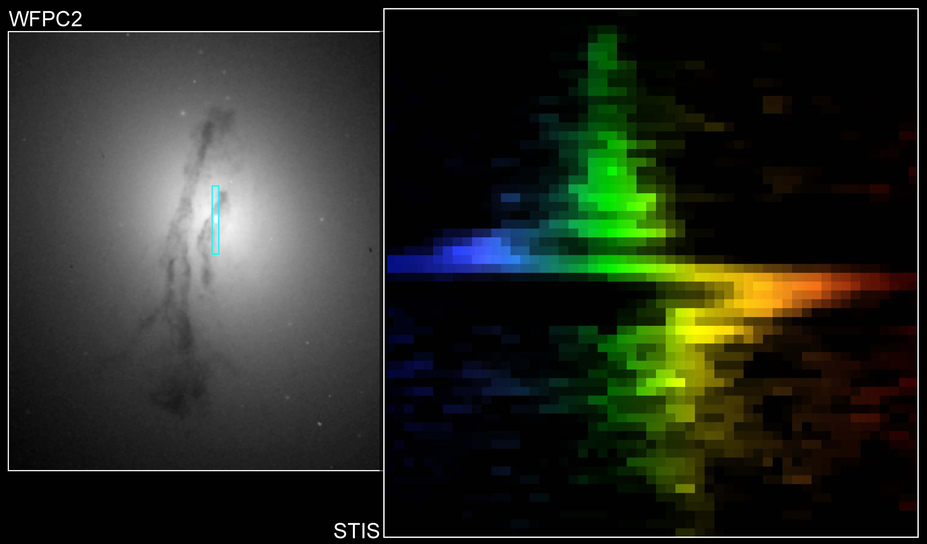
Spectrum and image of M84 courtesy of
Gary Bower, Richard Green (NOAO), the STIS Instrument Definition Team, and NASA
In the last decade, scientists have built devices which can detect the gravitational waves emitted from merging black holes (or neutron stars) directly. These are gravitational wave telescopes, which open a new window to the universe.
As of Oct 29, 2020, a total of twenty (20) events due to merging compact objects have been detected by LIGO. You can find a list of these confirmed sources at
Q: How many of these events involve only black holes? Q: How many involve only neutron stars?
Note that most of the events detected by LIGO involve relatively large masses, as stars go. Can you think of a reason to explain the detection of these high masses?
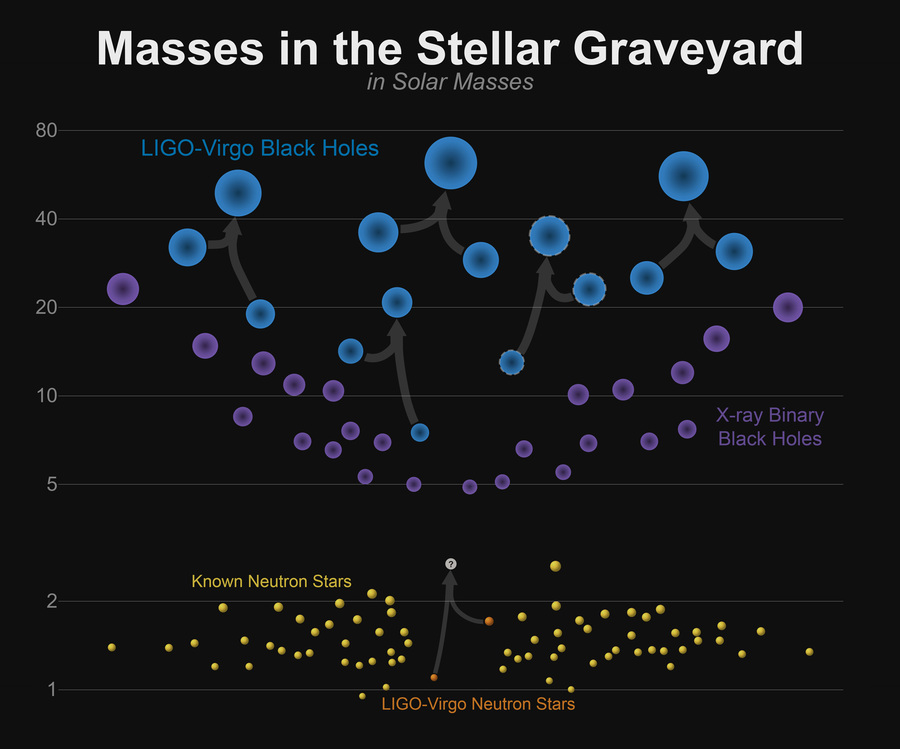
Image courtesy of
LIGO-Virgo/Frank Elavsky/Northwestern University
The LIGO collaboration sends out alerts to members of its private club of associated observatories when its software flags a possible event. Those lucky astronomers have a chance to search for any possible electromagnetic counterpart to the gravitational wave event before anyone else. Eventually, LIGO does make its list of "alerts" available to the public. You can go to their website and look for yourself.
 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.