 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
The goal for today is to add one more differential equation to our collection. This one will involve the change of luminosity with radius; in other words, it will involve the generation of energy inside a star. As we will see, stars fuse together atomic nuclei to release energy.
In the nineteenth century, geologists noted that some exposed rock faces contained large numbers of layered beds of material. They measured the rates at which sediment is deposited (and eroded) by rivers and oceans to estimate the duration of time required to create those formations. Their results indicated that the Earth must be at least hundreds of millions of years old. Certain observations of stellar motions suggested (less confidently) similar ages for clusters of stars inside the Milky Way.
It seemed reasonable to conclude that the Sun must have been shining for at least that long, in order to keep the surface of the Earth close to its current condition. But -- what source of energy could power the Sun for such a long time?
One possibility was gravitational contraction. If a very large cloud of gas collapsed to form a gigantic proto-Sun, and then continued to contract slowly, that decrease in size would correspond to a loss of gravitational potential energy (GPE). Perhaps some of that change in GPE turned into heat and kept the Sun warm.
A good idea -- but would it work? Let's find out.
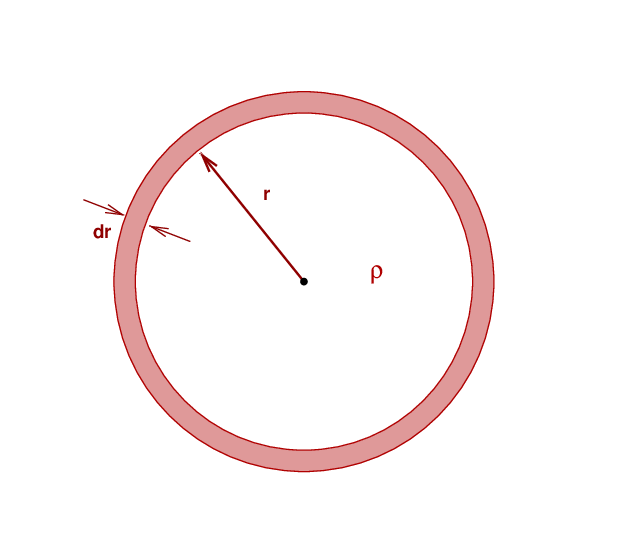
We'll start by determining the amount of gravitational potential energy a spherical object has. To simplify the procedure, we'll assume that the sphere has a uniform mass density ρ at all locations in its interior. This doesn't make a very realistic star, but it will provide a ballpark estimate. To compute this GPE, we'll first figure out the GPE of one thin little shell added to an existing sphere, then integrate over all the shells required to build up the entire object.
So, consider a sphere of mass density ρ and radius r. If we add a thin layer of the same density and thickness dr to its outer surface, how much GPE does this shell have?

Q: What is the GPE of this thin shell?
That's right,
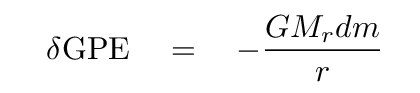
In a moment, we'll add up the contributions from all the shells in a sphere of radius R. But first, let's dig into that expression. We can re-write the mass of the little shell in terms of r and ρ.
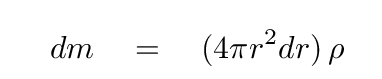
We can also express the mass of the sphere so far -- out to a radius r -- as
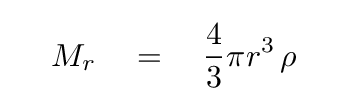
With these substitutions in place, we can integrate over all the shells to find the GPE of the entire sphere.
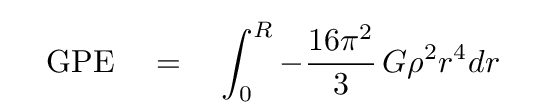
Q: Can you evaluate this integral?
You should end up with this expression.
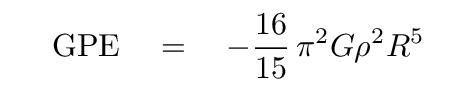
It is often more useful to write the GPE in terms of the mass M of the entire object.
Q: If you substitute into the above expression -- twice --
4 3
M = --- π R ρ
3
what is the result?
You should find
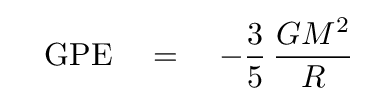
Phew. Okay, now we can see if the GPE released by a shrinking Sun might be able to provide the necessary power over hundreds of millions of years. Use the following values to compute the amount of GPE available if the Sun were to contract from an infinitely large cloud to its current size.
Q: What is the amount of GPE released by the contracting Sun?
Q: The current luminosity of the Sun is about 3.8 x 1026 J/s.
How long could this GPE power the Sun?
The nineteenth-century scientists came to the same conclusion as we did: gravitational contraction cannot power the Sun for hundreds of millions of years. So, they wondered, what was wrong: the estimated age of the Earth -- or the assumed source of energy of the Sun?
The first few decades of the twentieth century revealed a host of new physical phenomena: X-rays, photoelectricity, and radioactivity. Einstein's theory of special relativity revealed that mass could be converted to a very large amount of energy. Could some sort of nuclear reaction provide a solution to the puzzle of the Sun's power source?
Well, we know now that four hydrogen atoms can be smashed together (in a very complicated, multi-step procedure) to produce a single helium atom. In the process, a very small amount of mass is converted into energy. Using numbers from NIST Reference on Constants, Units, and Uncertainty ,
1 H m = 1.673 533 x 10-27 kg
4 H m = (you fill in)
1 He m = 6.646 479 x 10-27 kg
--------------------------------------------------
delta m = (you fill in)
What fraction of the original mass of 4 hydrogen atoms
is this lost in the process? Express as a percentage.
You should find that 0.7 percent of the mass of the 4 hydrogen atoms is lost; well, it's not really lost, it is turned into energy.
Q: How much energy is released by a single conversion of 4 H into 1 He?
Express in Joules, and in MeV.
So, we've found that 0.7 percent of the mass of four hydrogen atoms is converted into energy when they fuse into a single helium atom. That sounds promising, but is it enough to provide power for the Sun over the length of geological time? Let's find out.
Q: The mass of the Sun is M = 1.99 x 1030 kg,
and its luminosity is L = 3.8 x 1026 Joules/second.
Assume that 90 percent of this is hydrogen. Assume further
that all of the hydrogen may be converted into helium
(which is quite an overestimate).
How long could this fusion power the Sun's current luminosity?
Four hydrogen nuclei turning into one helium nucleus is not the only sort of fusion that can take place deep in stellar interiors. Under the proper conditions, almost any sort of atoms can fuse with others to form heavier elements -- and we will see a few examples later in this lecture.
However, there is something special about the conversion of hydrogen into helium. It is by far the most EFFICIENT sort of fusion reaction, when measured by the amount of energy released per nucleon (proton or neutron) involved in the process. When measured in this way, hydrogen fusion provides by far the most *pow* per particle.
A graphic illustration of this fact is the curve of binding energy. "Binding energy" is related to the difference between the sum of the masses of the input particles and the mass of the output fused particle(s); multiply that difference in masses by c2 and one ends up with the binding energy. It might just as well be called the "energy released per fusion".
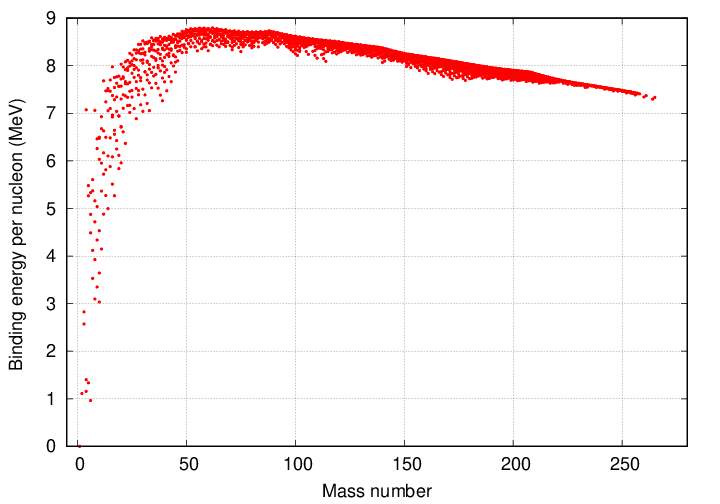
The vertical axis shows the binding energy divided by the number of protons and neutrons involved in final product. For example, look at the values for hydrogen and helium in the closeup below. The difference between helium (7 Mev) and hydrogen (0 MeV) is the amount of energy released per nucleon when fusion takes place. The helium nucleus has 4 nucleons (2 protons and 2 neutrons), so the total binding energy is about 28 MeV.
Yes, yes, the amount of energy released per hydrogen-to-helium fusion is a bit smaller, only about 26.8 MeV. I'm still trying to figure out this small difference....
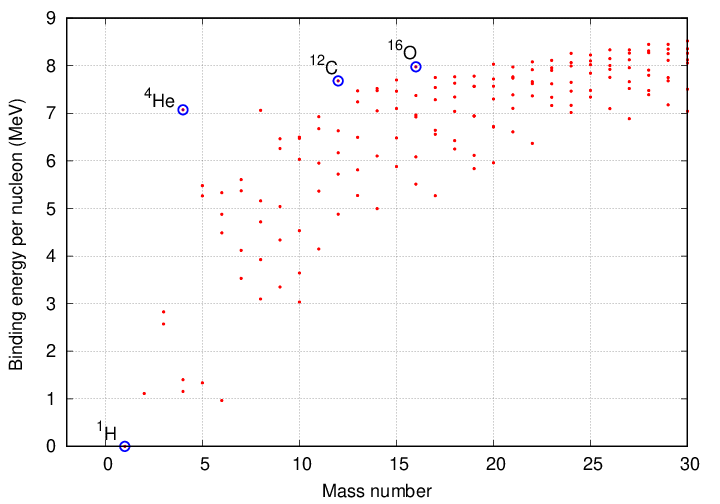
The next step (which we'll discuss a bit later) is to fuse three helium nuclei together to create a single carbon-12 nucleus. The increase in binding energy per nucleon is much smaller in this reaction: instead of jumping from zero to about seven MeV, the binding energy per nucleon increases by less than a single MeV. So one can produce energy by smashing helium together to create carbon, but the efficiency of the process is lower.
The curve of binding energy has a peak near atomic mass number 60, after which it gradually declines. One can interpret the graph in the following way: one can continue to produce energy by fusing lighter elements into heavier ones up to this peak ... but after that point, the efficiency will become negative. In other words, fusing together nuclei to produce a product with atomic mass greater than about 60 will REMOVE energy from the environment, instead of generating it. Those reactions would be endothermic, rather than exothermic.
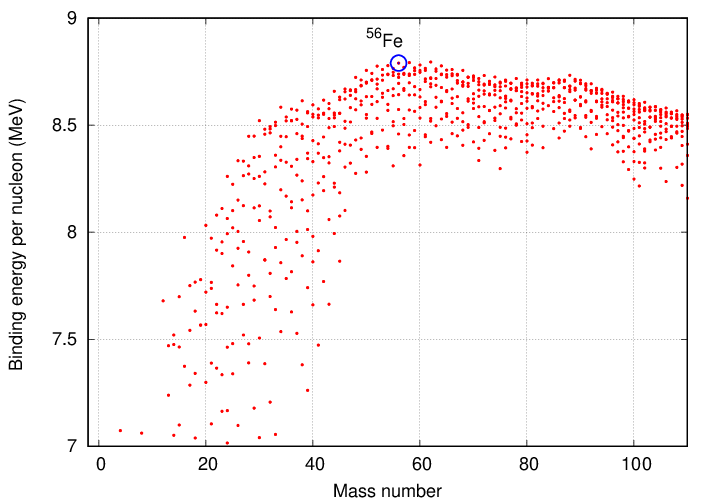
Note that iron (and its relatives nickel and cobalt) lies near the top of this peak. When we discuss supernovae, the fact that fusing iron to create heavier elements will NOT produce energy will become very important.
Of course, there is a way to extract energy from nuclei which are heavier than iron: one can break them apart via fission to release energy.
Let's look briefly at the physics of the interactions involved in the production of helium from hydrogen. If you'd prefer things at a simpler level,
Now, what factors will affect the rate of fusion reactions? Some of the most important are
The first two are pretty obvious, but what's so important about the number of protons in each nucleus? Well, protons are positively charged, and so they repel each other. In order to activate the strong nuclear force which binds nucleons together and will stabilize the fusion's product, one must push the positively-charged nuclei very, very close together. The larger the atomic number of each input nucleus, the larger the Coulomb force resisting their approach.
How can we overcome this repulsive electromagnetic force? If we increase the temperature, we can give each input particle enough kinetic energy to overcome the "Coulomb barrier" preventing their merger. But how high must the temperature rise to enable fusion reactions?
Under the laws of classical physics, one can derive a relatively simple expression for this critical temperature, given input nuclei of atomic number Z1 and Z2, and the critical separation r (around 1 fm = 10-15 m) at which the strong nuclear force takes over.
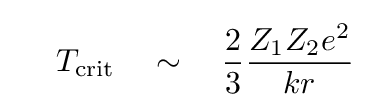
This threshold temperature clearly increases with the charge of the input particles. For hydrogen fusion, the equation yields a typical temperature of order 1010 Kelvin. Yikes!
Fortunately for stars (and us), quantum effects can reduce the required temperature. In particular, there is a small probability that two nuclei may "tunnel" through the Coulomb barrier and merge, even if they do not have enough kinetic energy to reach the critical separation r. If we apply the rules of quantum mechanics, we can derive a different expression for the critical temperature.
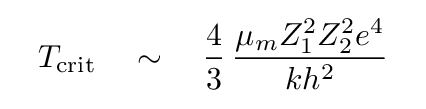
Here, μm is the reduced mass of the colliding nuclei
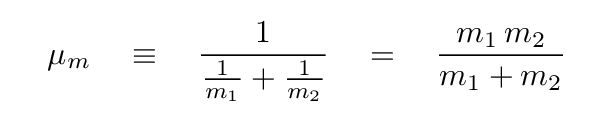
Now, note that this quantum expression involves an even stronger dependence on the atomic numbers of the input nuclei: each is SQUARED. The implication is clear: in order to fuse together heavier nuclei, one must provide a MUCH higher temperature.
Q: The threshold for H-H fusion is roughly 107 K.
What is the threshold for He-He fusion?
Okay, we've estabilished that there is a minimum temperature required for fusion reactions to take place. But how does the RATE of those reactions depend (if at all) on the temperature? If the temperature of a star's core increases by a small amount, how much will the rate of fusion change? This might be an important factor in watching our model of a star evolve over time.
The answer turns out to be ... complicated; see Carroll and Ostlie for a detailed discussion. For our purposes, however, it is sufficient to write a very simple expression that provides at least a rough approximation to the actual rate. When hydrogen fuses via the proton-proton chain reaction, the energy generation rate ε can be written
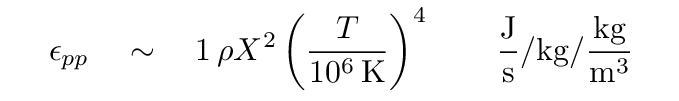
where X is the mass fraction of hydrogen and ρ the mass density of material in the core. Note the strong dependence on temperature: if the temperature doubles, the rate of energy generation increases by a factor of 16. Note also the units: after we multiply by the density ρ of the material, we are left with Joules per second per kg; so ε is the rate at which energy is generated per second, per kg of material.
The proton-proton chain is not the only way to bring four protons together to form a helium nucleus. In the CNO cycle, nuclei of carbon, oxygen and nitrogen act as catalysts to build, step by step, a helium nucleus. (You can see the individual reactions at shown in pictures. ) The rate depends not only on the mass fraction of hydrogen (X), but also on the average mass fraction of C, N and O (XCNO). This set of reactions is considerably more sensitive to the temperature:
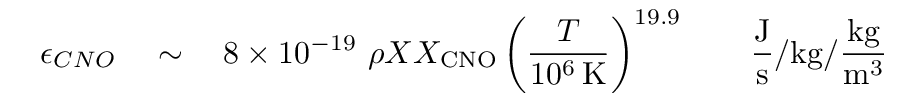
Q: Suppose the central region of the Sun has density ρ, temperature
T = 15 million K, and chemical composition X = 0.88
and XCNO = 0.02. Which process generates more
power -- the proton-proton chain, or the CNO cycle? How much more?
But if you really want to see some strong temperature dependence, consider the process by which some stars can fuse helium into carbon. Because the product of two helium -- 8Be (beryllium) -- is so unstable, it will decay back into helium unless a third helium nucleus happens to strike it immediately. Therefore, this reaction is more of a three-body encounter than the usual two-body collision, and is known as the triple-alpha process. The form of the equation below reflects this requirement that three particles meet: it includes a factor of density squared. The rate of this reaction increases as temperature to the 41st power!
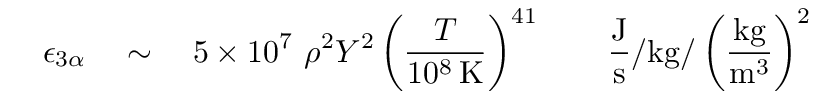
Note also the change in the normalization of the temperature term. Instead of being expressed in "millions" of degrees, here the base unit is "hundreds of millions" of degrees. Because the particles involved have more electric charge, the Coulomb barrier is considerably higher.
Q: The threshold for H-H fusion is roughly 107 K.
Assume that one pair of helium nuclei merge to form
a beryllium nucleus, which is then quickly approached
by a third helium nucleus.
Estimate the temperature threshold for Be-He fusion.
Okay, now we know how the rate at which fusion reactions release energy depends on other factors. What can we do with this knowledge? How about writing down the third of the five differential equations we need to build a stellar model?
We have defined the energy generation factor ε as "the power generated per unit mass;" that is, per gram or per kilogram (our examples earlier in this lecture are in MKS units, so per kg). Consider a thin spherical shell within the star at some particular radius r, inside of which the temperature, density, and other properties are all identical.
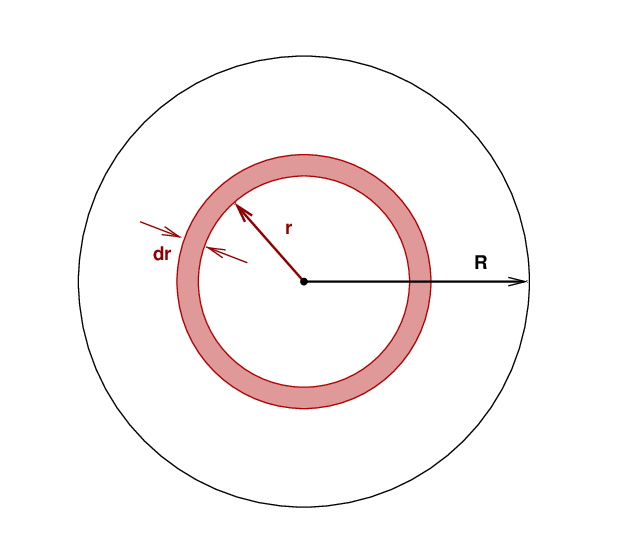
We know the mass of this thin shell:
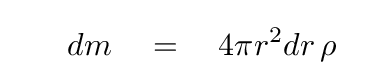
That means we can compute the power generated within this shell:
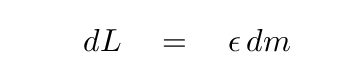
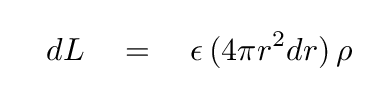
With a little re-arranging of terms, we can write down the third differential equation, which describes how the luminosity of a star changes as one moves outward from the center by a distance dr.
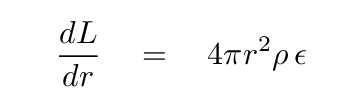
Keep in mind that in ordinary stars, energy is generated only in the central regions. For the great majority of the shells in a model, the temperature will be too low for fusion to take place. Therefore, this term dL/dr will be zero. In other words, the luminosity of a star remains constant as one moves out away from the core toward the surface.
 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.