 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
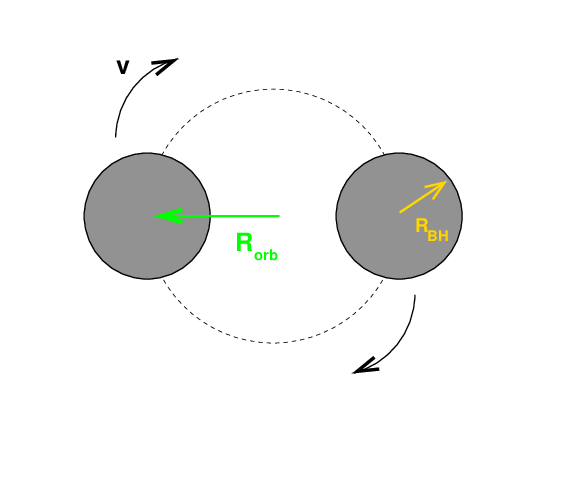
We need a source of gravitational waves. A pair of black holes, orbiting very close to each other, should do the trick. The picture looks basically like this:

Let's pick some representative parameters, similar to those of real gravitational wave systems detected by LIGO.
Mass of each black hole M = 10 solar masses = 2 x 1031 kg
2 G M
Radius of black holes RBH = -----
c2
Radius of orbit Rorb = 2 RBH
Velocity in orbit v
Distance from Earth D = 340 Mpc
Can you compute the values of these parameters? My answers.
Now, two of the most important properties of a gravitational wave are
For our representative system shown above, what are these properties?
Q: What is the PERIOD of the wave at this moment? Q: What is the FREQUENCY of the wave?

From which we can estimate a frequency of 200 Hz.
Is that correct? Well, when LIGO reported a detection of two "lightweight" black holes merging in June, 2017, the "chirp" signal it recorded looked like this:
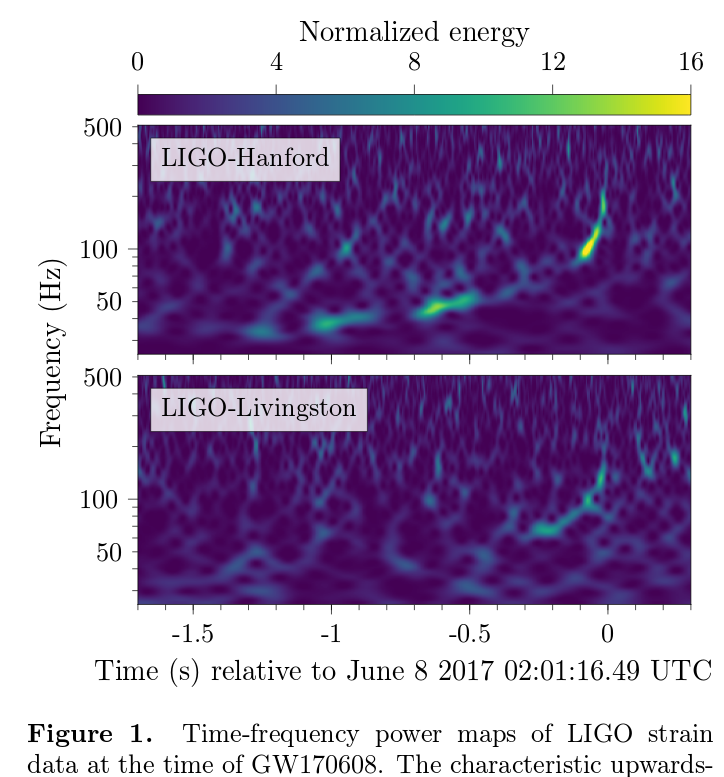
Figure 1 taken from
Abbott et al., arXiv 1711.05578 (2017)
Now, the amplitude of the wave is another matter. The real answer requires some complicated calculations, but to a rough approximation, we can say that the dimensionless strain h of a wave generated by some mass M moving at some speed v, and observed at distance D, is roughly
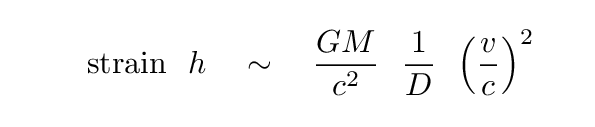
The first term has units of length -- it's roughly the size of the event horizon of the mass; the second term, which includes the distance between source and observer, has units of one-over-length; and the third term is clearly a pure ratio. That means that this "strain" h must have no units.
Q: What is the STRAIN of the wave observed on Earth?
That's ... a very small value.
We are clearly looking for a very small signal. But how exactly can one detect any gravitational wave, big or small?
The answer is based on the way that a passing gravitational wave will interact with space and matter. As a wave flies through some region of space, it causes space to contract in one perpendicular direction (and expand in the other), and then expand in that perpendicular direction (while contracting in the other).
For example, if we put this portrait on the wall, and then send a gravitational wave flying into the wall, we would see it distort as ... (click on the image).
One way to detect such a wave is to use an interferometer with two long arms. Light waves from a single laser a split, so that half run down one arm and half run down the other. After bouncing off mirrors at the end of each arm, the two beams are combined at a sensor. We can adjust the length of the arms so that -- when no gravitational waves are present -- the two beams combine DESTRUCTIVELY, yielding a big fat "nothing" at the sensor.
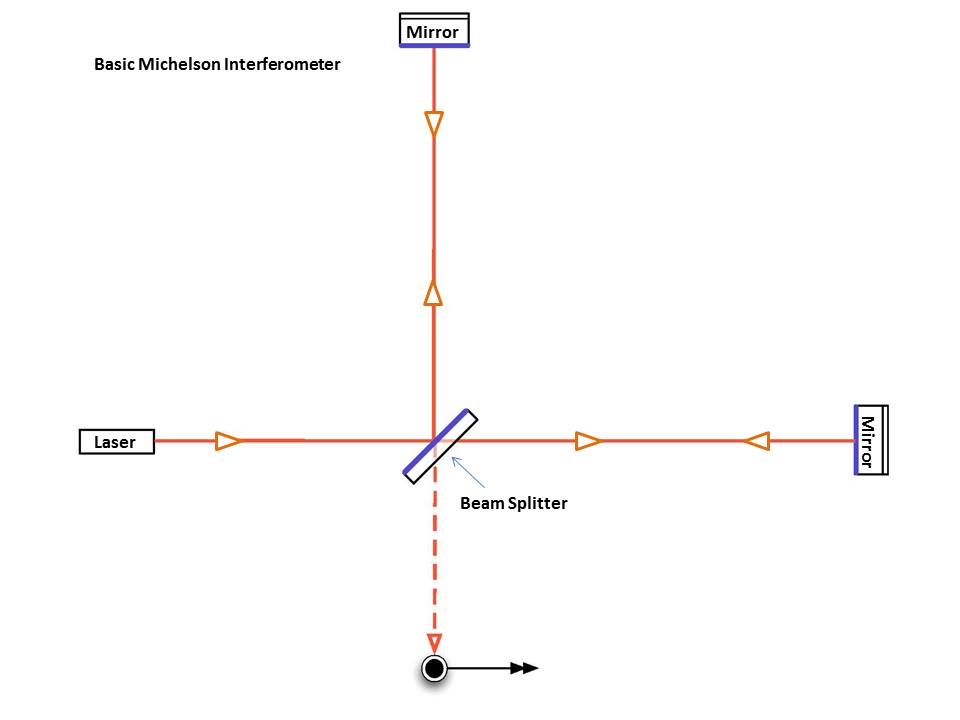
Image courtesy of
LIGO
On the other hand, if a gravitational wave happens to fly through the interometer from "above" or "below" (perpendicular to the arms), then it will cause the length of the arms to change. That, in turn, will cause the path difference between two light beams to change, which will ruin the perfect destructive interference: our sensor will detect some light! And if the gravitational wave has a certain frequency, it will impress that frequency on the changing length of the arms, and hence on the output of the sensor.
"Hey!", you might interject at this point, "even if the length of the arms change due to the gravitational wave, doesn't the wavelength of the waves change too, and by exactly the same amount? Why should any interference occur?"The answer is, yes, the wavelength of light DOES change as the gravitational wave passes. However, the device will still create a signal at the detector. One simple view that might help you to understand is based on timing: consider the crests of two beams that enter the device just as a gravitational wave appears. One travels down a shorter leg, and the other down a longer leg -- so the crests do not arrive at the detector at the same time -- so they can't interfere in the normal way to cancel each other out.
If you seek further explanation, look at
- Chapter 27 of Kip Thorne's lecture notes from CalTech. Read section 27.6 in particular.
- If light waves are stretched by gravitational waves, how can we use light as a ruler to detect gravitational waves? an article in American Journal of Physics by Peter R. Saulson.
Well, that's the basic idea, anyway. A real interferometer like LIGO is a bit more complicated. Okay, a LOT more complicated.
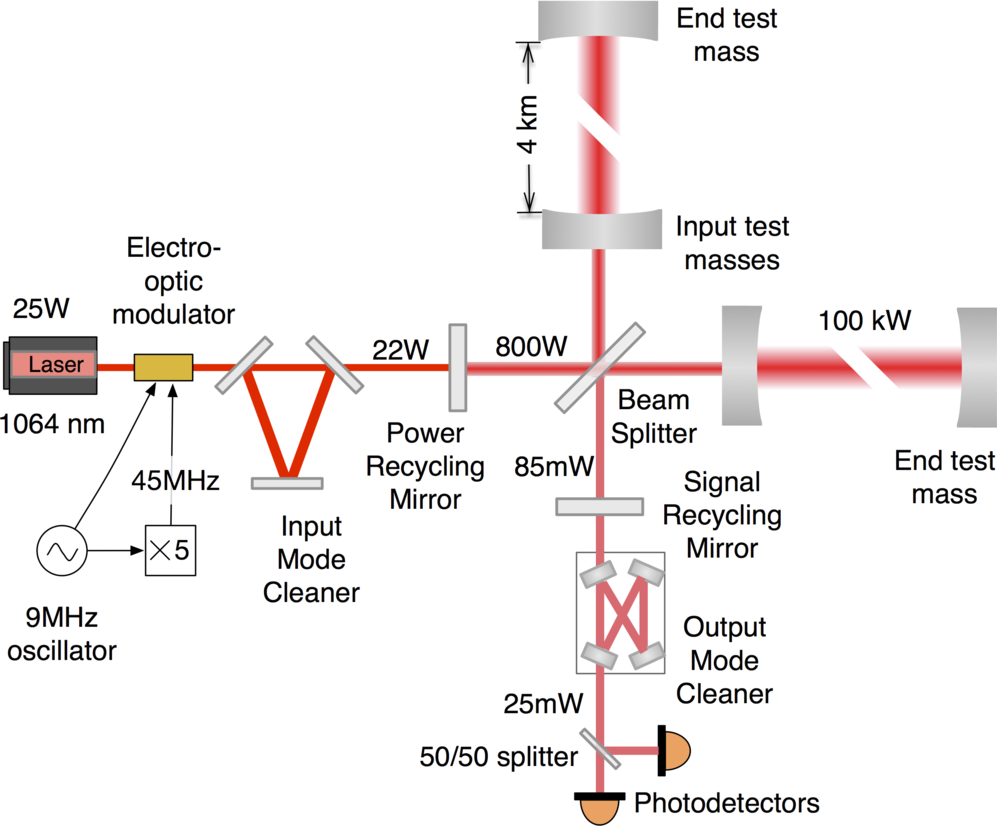
Image courtesy of
LIGO
But before we talk about the real LIGO any more, let's try to figure out one very important feature of an interferometer-type gravitational wave detector: how long should the legs be?
If our interferometer has legs of length L, and a gravitational wave of strain amplitude h passes through it, the change in the length of each leg will be
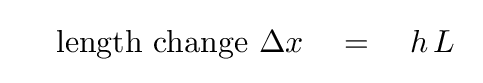
We can turn the equation around to compute the required length L if we have some particular minimum detectable change in length Δ x. Can you fill in the table below?
Min detectable change Min leg length
Δ x L
-------------------------------------------------------
1 m
(vis light) 500 nm
(atom nucleus) 1 fm
-------------------------------------------------------
Yikes! These are all really large!
It turns out that the real LIGO has legs which are about L = 4000 m = 4 km long.

Image courtesy of
Caltech/MIT/LIGO Lab
Q: What is the change in leg-length of LIGO due to our
canonical gravitational wave?
That is a TINY change in length! But the clever folks at LIGO have increased it, in effect, by causing photons to bounce back and forth multiple times (about 100-200 times) before finally interfering with each other.
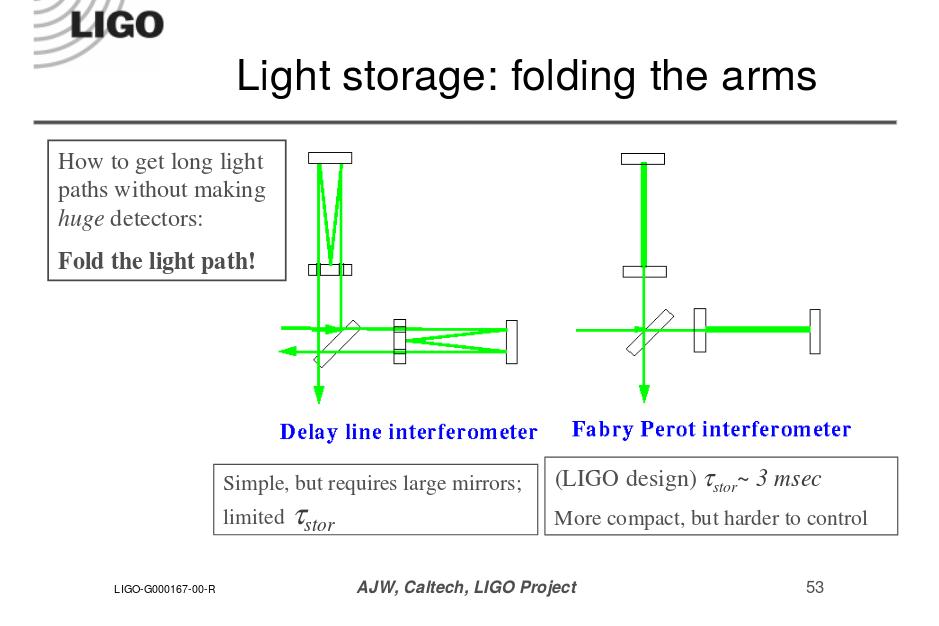
Image taken from
Alan Weinstein, CalTech
Q: Assume that a single photon travels for 3 msec before interfering
with its partner. What is the "effective" change in
leg length due to our canonical gravitational wave?
That's still a TINY change -- much smaller than the size of an atomic nucleus. But the folks at LIGO are able to detect it! Look!
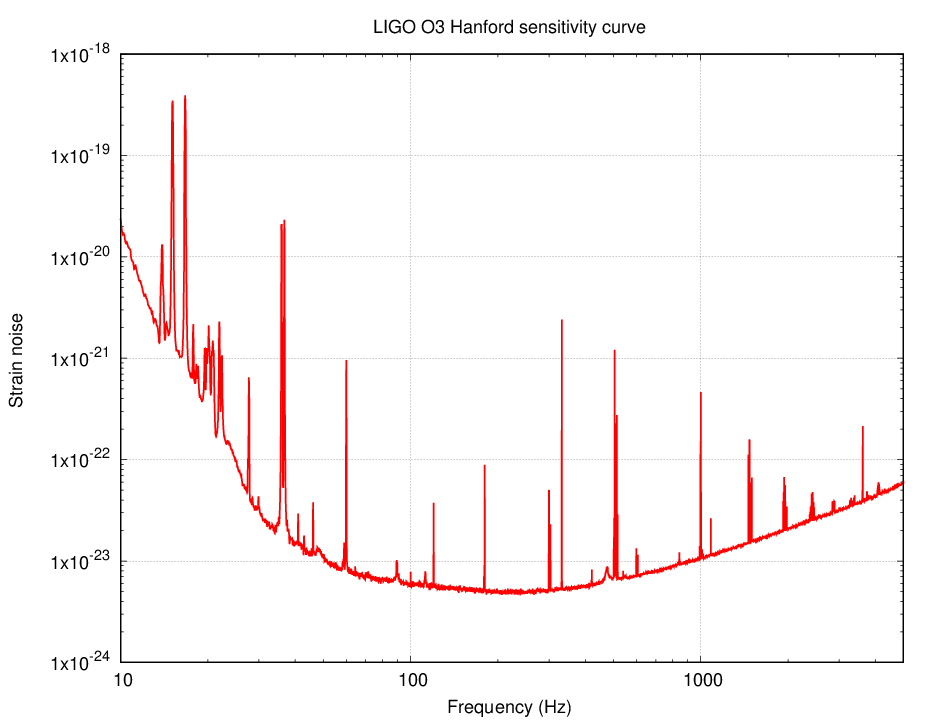
Image based on
LIGO Document T1500293-v13
Of course, it's a very complicated business, and a feat of engineering. For example, the light beams must travel through a vacuum to avoid scattering off air particles. So, each leg is a 4-km-long vacuum chamber:

Image courtesy of
Caltech/MIT/LIGO Lab
The mirrors must be protected from vibrations, so the engineers have created a very sophisticated apparatus for isolating them from disturbances. The mirror, of mass 40 kg, is the FOURTH in a series of pendula. The other objects in the chain have a total mass of about 320 kg; acting as a system, they damp out most of the vibrations and allow the mirror to hang freely.
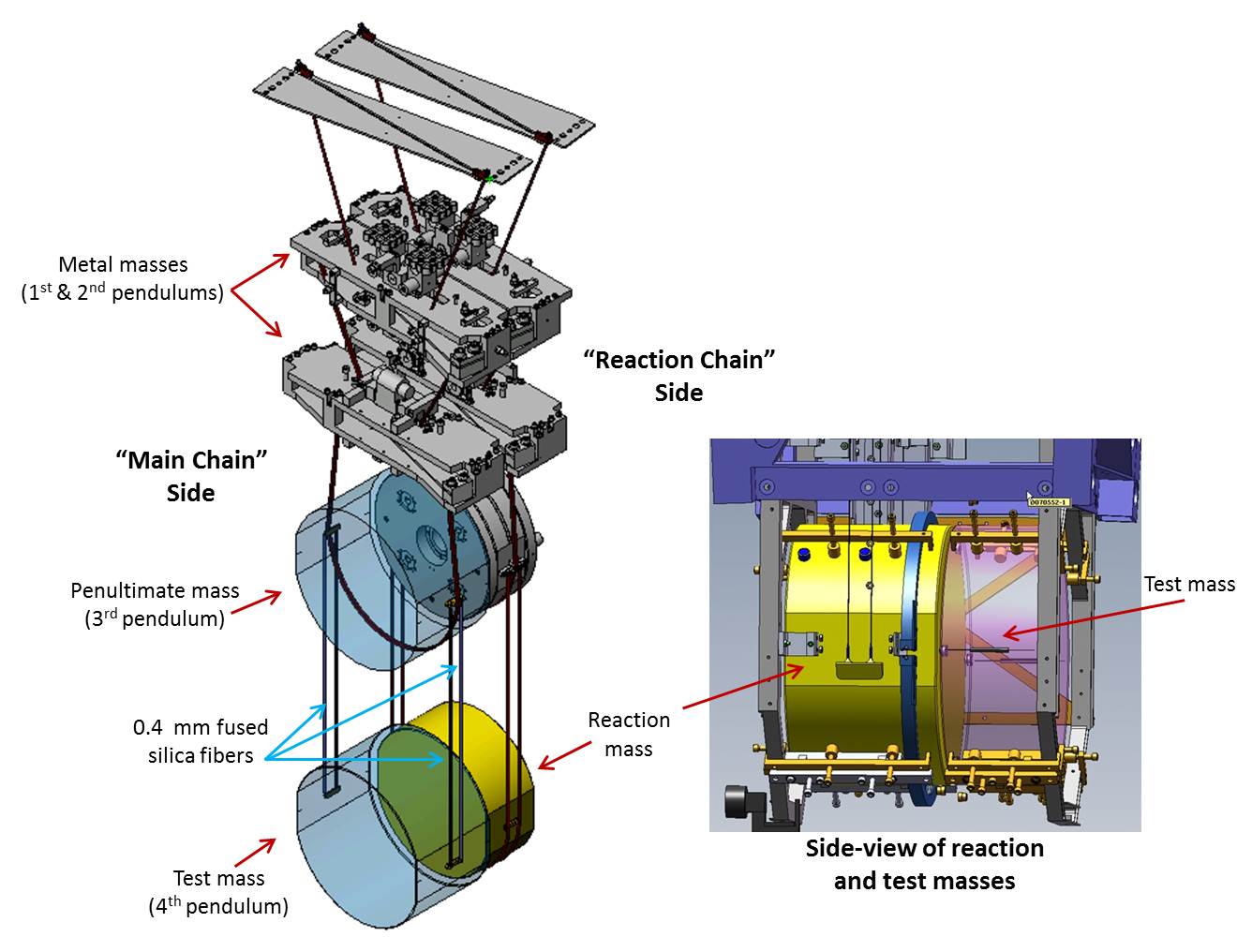
Image courtesy of
LIGO collaboration
Note the rather fragile-looking connection between each mirror and the fibers of the pendulum:

Image courtesy of
LIGO collaboration
Suppose that we do detect a gravitational wave with LIGO or one of its kin. The interferometer will tell us the AMPLITUDE of the wave, and the TIME at which it passed the Earth ... but what about the DIRECTION from which it came? How well can we figure out the location of the wave's source in the sky?
The problem is localizing a GW source is a tricky one. It begins with the response of a single interferometer to gravitational-wave radiation. Remember the shape of the interferometer is an "ell".

Image courtesy of
LIGO
This acts like an antenna: it is most sensitive to gravitational-wave radiation coming from directly above or below the plane of the "ell", but can still detect waves from most other directions at a reduced level.
Q: Are there any directions to which the antenna
has ZERO sensitivity?
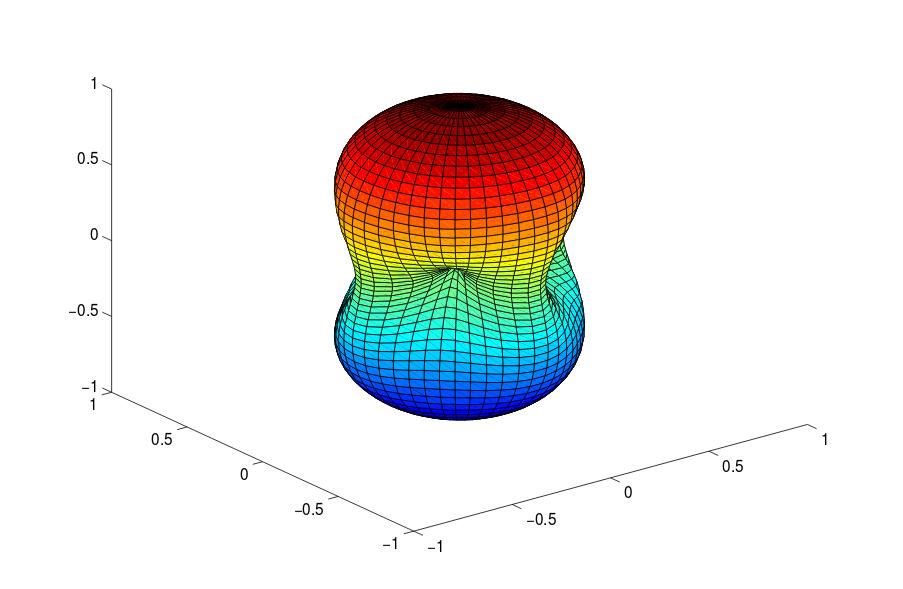
Taken from Figure 4 of
Sathyaprakash and Schutz, Living Rev. Relativity 12, 2 (2009)
The figure below shows another way to describe the sensitivity of the Hanford, Washington, LIGO antenna to gravitational waves.
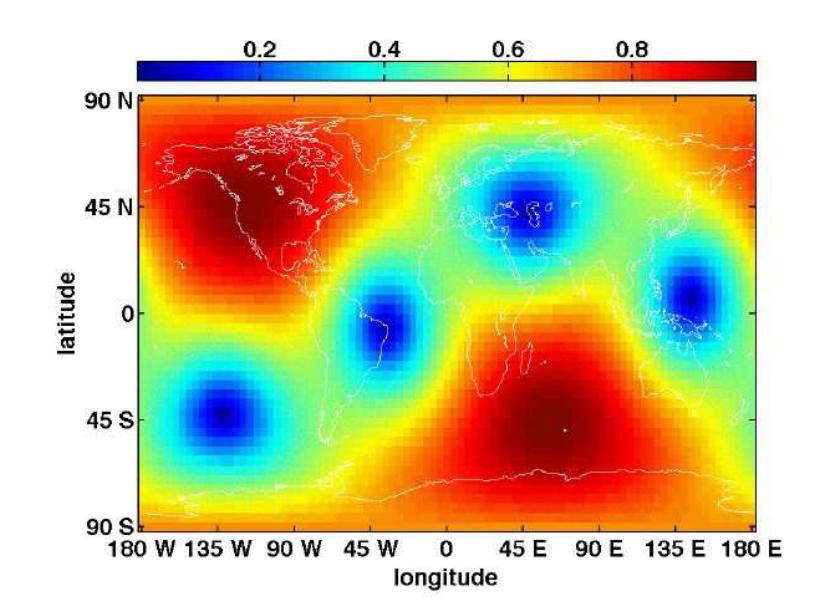
Taken from Figure 1 of
Hayama and Nishizawa, Phys Rev D 87, 062003 (2012)
Clearly, a single interferometer will not provide much guidance to the direction of a signal. That's why LIGO was designed from the start to have two interferometers, one in Hanford, WA, and the other in Livingson, LA.
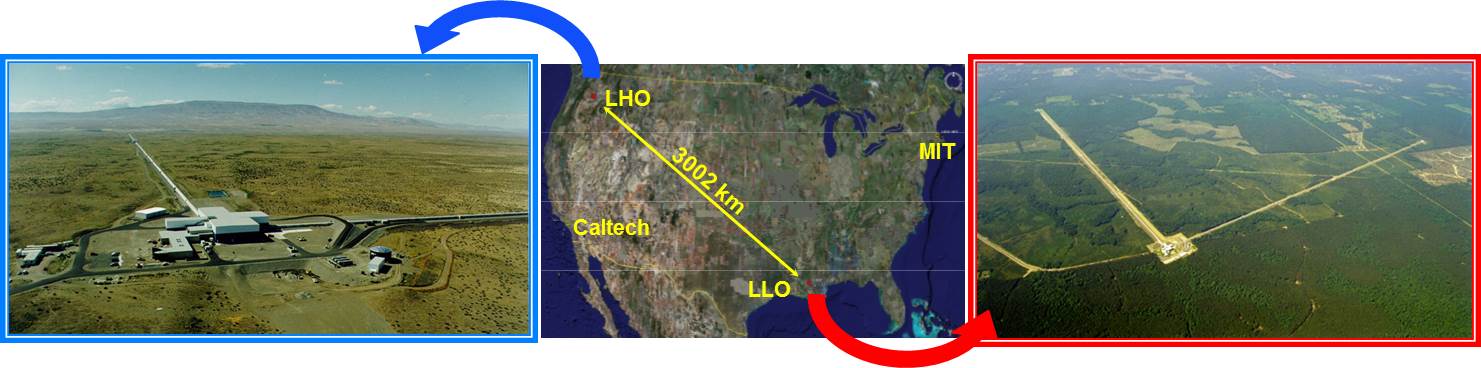
Image courtesy of
Caltech/MIT/LIGO Lab
Having two detectors helps in two different ways:
The second of these effects is the more important. Using triangulation between the two sites, astronomers can estimate the direction of the source with some precision. The figure below shows the regions to which a two-detector signal might be localized, from a simulated signal (which is located at the star in each figure).
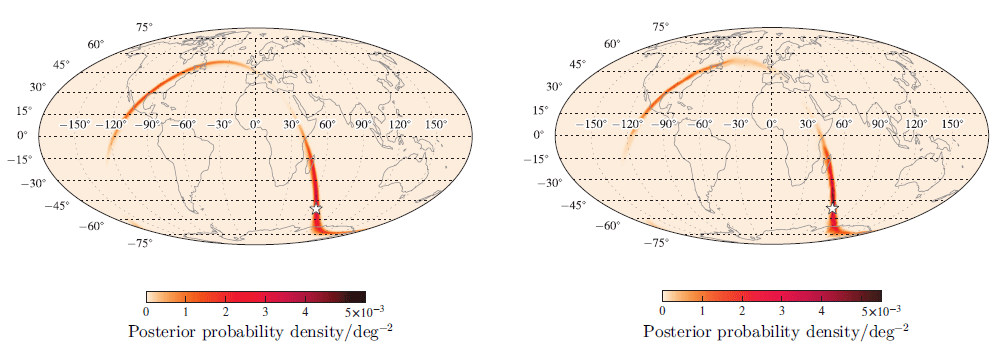
Figure 5 taken from
Abbott et al., "Prospects for Observing and Localizing
Gravitational-Wave Transients with Advanced LIGO and Advanced Virgo",
Living Rev. Relativity, 19 (2016)
If there are three detectors, the region of the sky from which the signal arose can be determined even better. Each pair of detectors yields a thin circular annulus around the sky, and the intersections of the annuli (S and S' in the figure) mark the most probable locations of the source.

Figure 4 taken from
Abbott et al., "Prospects for Observing and Localizing
Gravitational-Wave Transients with Advanced LIGO and Advanced Virgo",
Living Rev. Relativity, 19 (2016)
Now, these regions may be only a small fraction of the entire sky ... but the entire sky is BIG -- over 40,000 square degrees! Since the big, powerful telescopes which can see faint sources tend to have small fields of view, of just a fraction of 1 square degree, it can still be tough to locate the optical (or radio, or X-ray) counterpart of a gravitational wave source.
Consider the case of GW170817, a binary-black hole merger detected in August, 2017. This was the first real event to be observed by three antennae: both LIGO sites, and the VIRGO detector near Pisa, Italy. The signal arrived first in Livingston, the 8 ms later in Hanford, and 14 ms later in VIRGO.
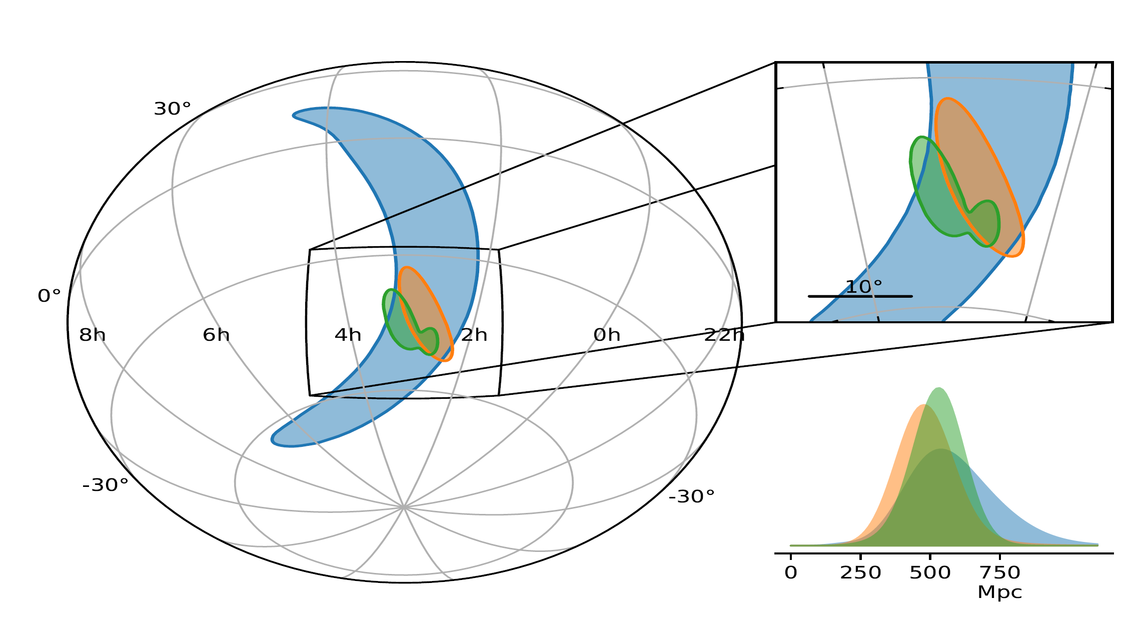
Figure 3 taken from
LIGO's index of GW170814 publications
The figure below shows the localizations of some the current gravitational wave detections; most were made only by the two LIGO antennae, but the two most recent, GW 170814 and GW170817, include VIRGO as well. Note how much smaller they are.
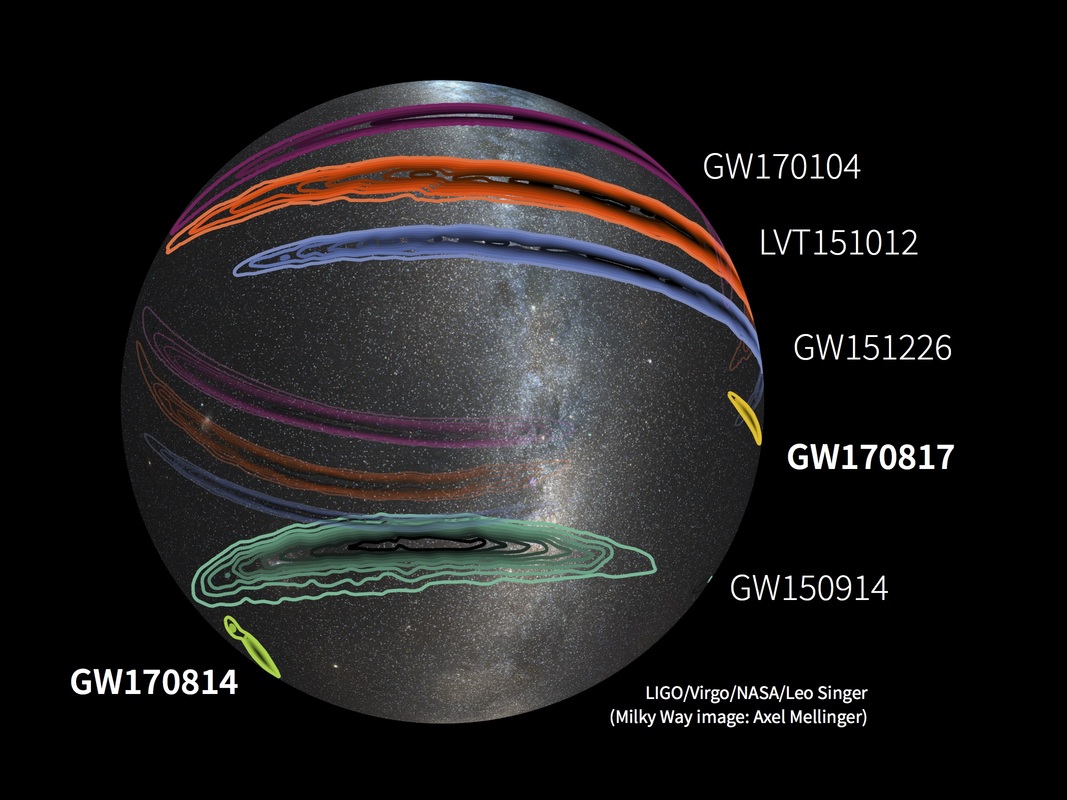
Figure courtesy of
LIGO/Virgo/NASA/Leo Singer
GW170817 was a merger of neutron stars, producing a counterpart in electromagnetic radiation. The combined LIGO Hanford + LIGO Livingston + Virgo localization yielded a relatively small region for optical (and radio, and X-ray) astronomers to search.

Image courtesy of
LIGO's GW170817 information page;
LIGO/Virgo/NASA/Leo Singer
As a result of this relatively small search area, astronomers were able to pin down the position of the counterpart within less than one day from the detection of the gravitational wave. In the figure below, the short vertical dashes represent the times when information was reported via GCN Circular.

Taken from Figure 2 of
Abbott et al., ApJL 848, 12 (2017)
 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.