Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Remember these swinging eggs? They represent what's called a "loosely-coupled" system. Today, we'll find out what that means, and how to analyze such systems.
Video demonstration courtesy of
Sixty Symbols
(or local copy)
Let's revisit a system we've analyzed already, but add a small twist.
This is the same old pair of blocks sliding on a frictionless floor, connected by three springs. We've already analyzed the behavior of this system -- twice, in fact:
But in all that time, we always made one simplifying assumption: that all the springs were identical. With that assumption, the motion of the two blocks ends up looking, well, sort of confusing. Each block slides back and forth in some not-quite-simple way, but at least the two blocks have equal amplitudes and frequencies.
Even though this choice of springs makes the problem relatively easy to solve, it doesn't really help us (or me, anyway) to understand what's going on.
So, let's add a twist: let's make the middle spring weaker than the side springs. We'll use the symbol k to denote the force constant of the side springs, and kc for the middle, or "coupling" spring; after all, it is the component that "couples" the two blocks together.
To start our analysis, we determine the forces on each of the two blocks. I'm going to be lazy and skip the vector signs.
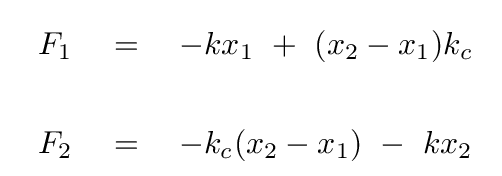
The next step is to group together all the terms including x1, and all the terms including x2. Let's also divide both sides by the masses of the blocks, and put the accelerations on the right.
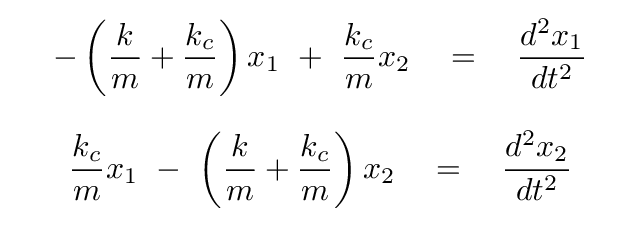
Okay, it's time for you to do some work.
Write these two equations in the form of a matrix equation,
with a vector representing the positions of the
two blocks.
Right.
The next step is to assume that there is some linear combination, s, of the real coordinates, x1 and x2, which will yield SHM in this system. Let's represent this linear combination by the (as-yet) unknown proportions a and b, like so:
If our assumption is correct, then when expressed in terms of this new normal coordinate s, the right-hand side of the equation will simply be some negative multiple of s itself.
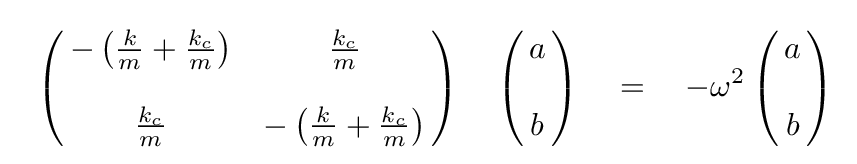
Well, this is a familiar situation. We have a matrix equation involving the unknown coefficients, a and b, which convert the real coordinates of the blocks into normal coordinates. This equation also has the unknown frequencies ω of the normal modes with which the system will oscillate, when expressed in terms of the normal coordinates.
So, two equations, and three unknowns. Don't worry, it will all work out in the end.
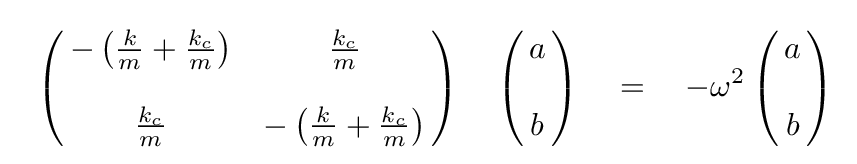
However, there are a lot of terms, due to the difference between the side-spring force constants k and the middle spring's value of kc. The algebra moving forward will get messy, and it would be easy to confuse those spring constants. Let's make things a bit simpler by defining some variables we'll use just to solve this equation.
Perform the matrix multiplication, and write down the two
equations which result.
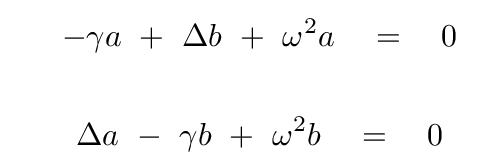
As we have done before, we simplify by eliminating one of the variables. The first equation gives us b in terms of a.
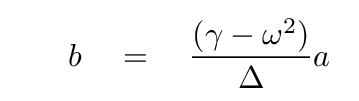
Plug this into the second equation to get
Q: Simplify this equation.
You can divide both sides by a, as long as you promise not to allow a = 0 to be an acceptable part of the solution. With that, and collecting terms, we end up with an equation involving a frequency to the fourth power.
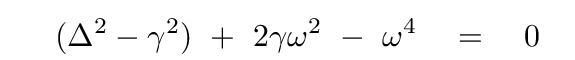
I don't like variables to such high powers, so I'll define one more new quantity:
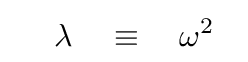
which converts our result into a nice, simple, quadratic equation:
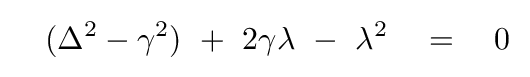
Q: What are the values of λ which solve this quadratic equation?
a) λ = ± 2 γ
b) λ = 2 γ ± Δ
c) λ = 4 γ ± Δ
d) λ = γ ± Δ
In other words, there are two eigenvalues of the matrix equation:
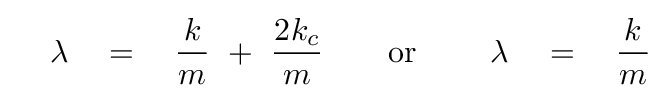
These eigenvalues correspond to the frequencies of the normal modes:
You should recognize the first frequency: that's just the frequency of an isolated mass m attached to an isolated spring of force constant k.
The second frequency is higher. Apparently, the presence of a second spring attached to a block leads to somewhat higher accelerations and thus higher frequencies.
The next step, finding the eigenvectors which correspond to each of these eigenvalues, is relatively short and easy. All we have to do is to insert one of the eigenvalues into the equations which resulted from our matrix multiplication.
In other words, into these equations,
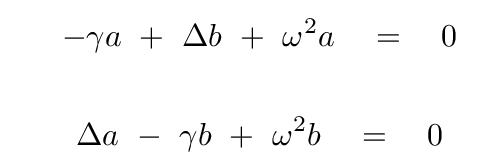
we insert one of the eigenvalues. Let's pick ω2, and put it into the first equation.
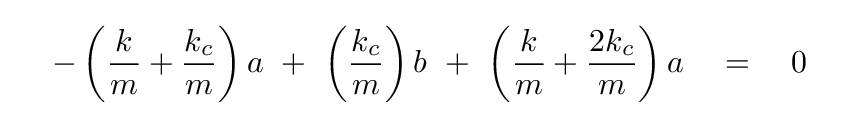
Q: Solve for b in terms of a. What is the eigenvector
which corresponds to eigenvalue ω2?
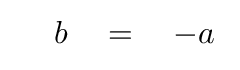
The eigenvector s2 corresponding to the eigenvalue ω2 is therefore
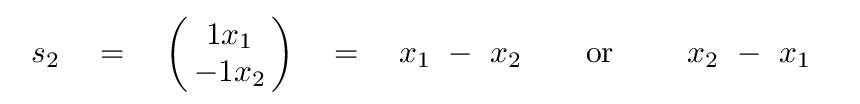
Phew. That wasn't so bad.
Can you go through the same steps to find the eigenvector s1 which corresponds to the eigenvalue ω1?
Q: What is the eigenvector s1?
For the frequency ω1, you should find that
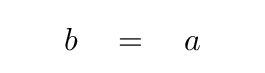
and therefore the eigenvector s1 is
Now that we have found the values of the eigenvalues and the eigenvectors, we can write down the simple equations which describe the motions of the normal coordinates as a function of time:
These can be expressed in terms of the real positions of the two blocks, too.
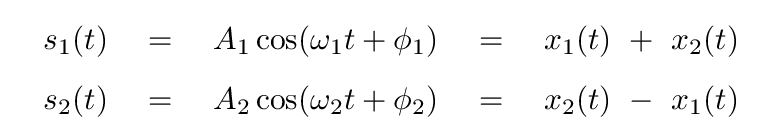
And we can invert the expressions to write the real positions in terms of the normal coordinates.
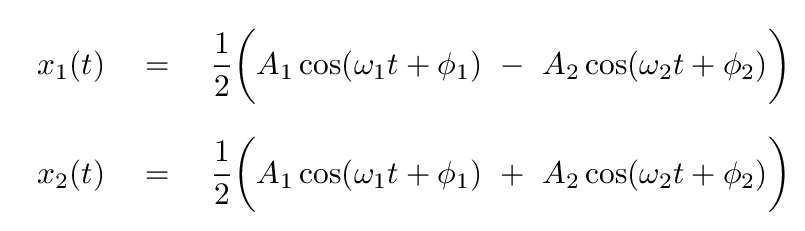
The values of the constants of integration, A1, φ1 and A2, φ2, can be determined from the initial conditions. For today's purposes, we'll pick a simple set of initial conditions: at time t = 0
In this particular case, the equations of motion for each block simplify to
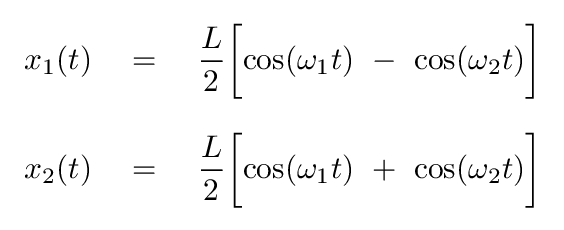
Now, if we choose a middle spring which has the same force constant as the side springs, we get motion that looks like this:
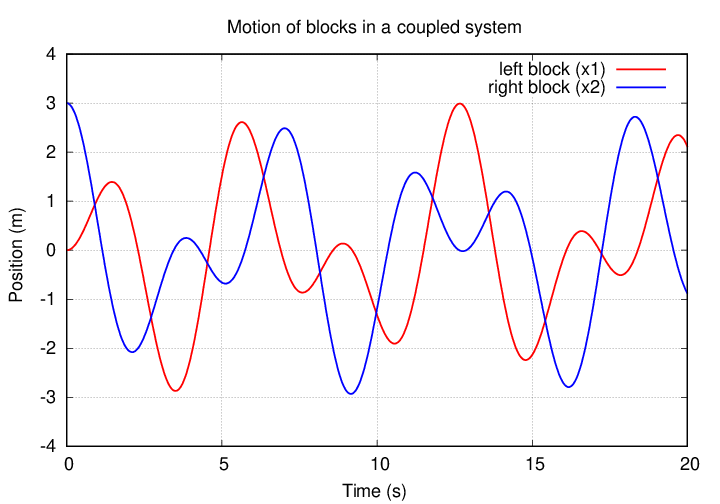
But things are more interesting -- and reveal more of what's happening -- if we choose a weaker middle spring. Let's choose one with just one-tenth the strength of the side springs: kc = 0.1 k. When we start, the right-hand block (blue) is moved away from its equilibrium point, and the left-hand block (red) is still at the equlibrium point.
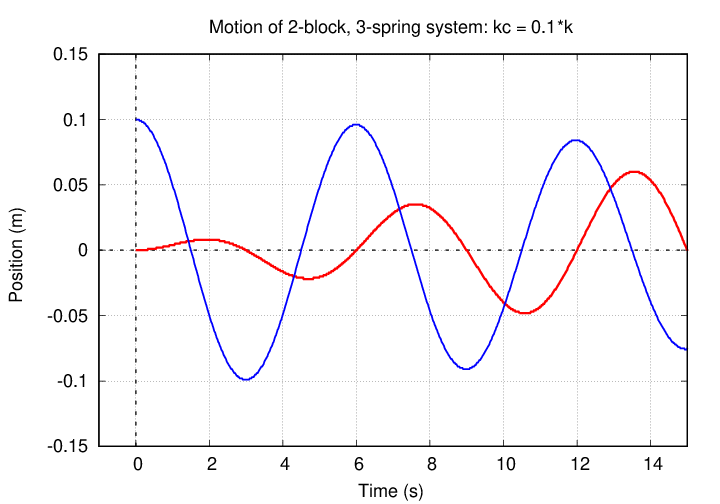
You can see that, at first, the blue block is moving with a large amplitude, but the red block barely moves in response. Slowly, though, the red block's motion grows.
Q: Why does the red block start to move?
Because the motion of the blue block causes the weak middle spring to exert small forces on the red block. In other words, the blue block is forcing the red block to move.
We discussed forced harmonic motion a few weeks ago. You may recall that the response of an object to a driving force depends on the relationship between two things:
Q: What is the (approximate) natural frequency of the red block? Q: What is the (approximate) driving frequency of the blue block?
Aha. When the driving frequency is close to the natural frequency ω0 of a system, we expect that the motion of the object will lag behind the driving force by a phase difference of 90 degrees.
Well, look at the motion of the two blocks at early times.
If we follow the blocks for a longer period, we see that eventually, the red block achieves a larger amplitude, and the blue block nearly stops moving ... but then the RED block starts to drive the blue block back into motion again.
Q: At time t = 5, which block is "leading" the other? Q: At time t = 35, which block is "leading" the other?
What's happening here is that the two blocks are taking turns "driving" the other.
Let's look at the frequencies here. If we adopt values of m = 1 kg and k = 1 N/m, and so kc = 0.1 N/m, then we can compute the frequencies of the normal modes.
Q: What is angular frequency ω1, Q: What is the frequency (in Hz) f1? Q: What is angular frequency ω2, Q: What is the frequency (in Hz) f2?
If two sets of oscillations with different frequencies meet, their combination will form beats. The beat frequency will be equal to the difference in the two frequencies.
Q: How long does it take for the maximum amplitude
of motion to switch from blue block to red block?
Q: What is the interval between maximum amplitudes
of motion for the blue block?
Now, suppose we were to choose an even weaker spring to join the two blocks.
Q: What would change if we were to place an even weaker
spring between the two blocks?
Let's choose a "coupling spring" with a force constant of just 2 percent that of the side springs: kc = 0.02 N/m. When we release the blocks from rest, the blue block has a nearly constant amplitude of oscillation, while the red block very slowly creeps away from its equilibrium position.
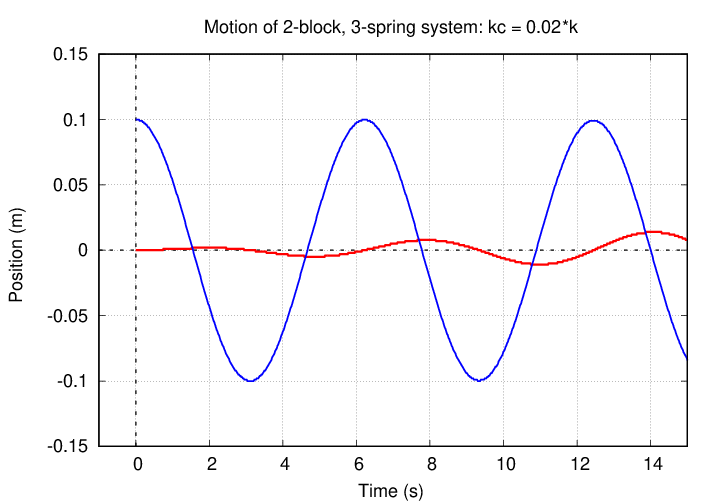
Why does the red block respond so slowly to the motion of the blue block? Because the spring joining them exerts such a small force!
But if one waits long enough, the red block will start to overtake the blue block.
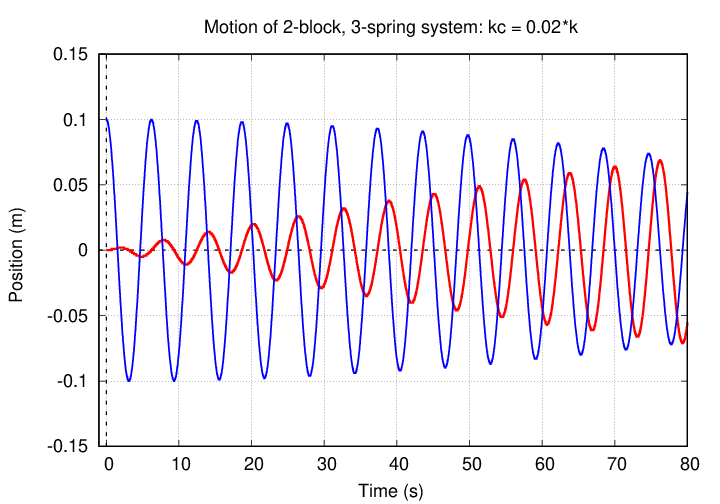
Q: What is angular frequency ω1, Q: What is the frequency (in Hz) f1? Q: What is angular frequency ω2, Q: What is the frequency (in Hz) f2?
Right. The frequencies are now
The difference between these -- the beat frequency -- is 0.00315 cycles/s, corresponding to a period of 317 seconds.
If this special "loosely coupled" system seems interesting to you, perhaps you might try one of the Extra Credit projects:
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.