Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Want to see coupled oscillators in action? Click on the picture below.
Video demonstration courtesy of
Sixty Symbols
(or local copy)
Over the next few weeks, we will look carefully at systems which contain more than a single oscillator; not only that, in these systems, the actions of one item can and do affect the actions of the other(s). The result will be a set of differential equations which contain bits and pieces of each other. How in the world will we deal with such a complex situation?
Well, let's take it slowly. We'll begin with a very simple system, containing only two moving objects and lots of symmetry. Once we understand how to express its motion, perhaps we can use the lessons we've learned to solve more complicated systems.
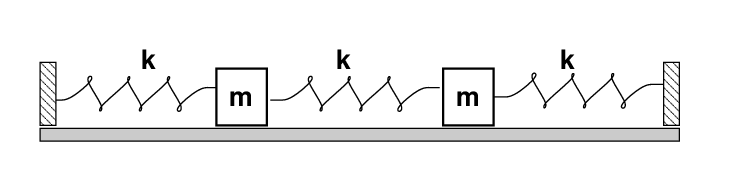
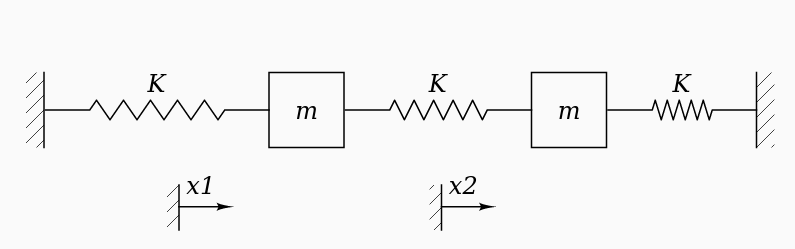
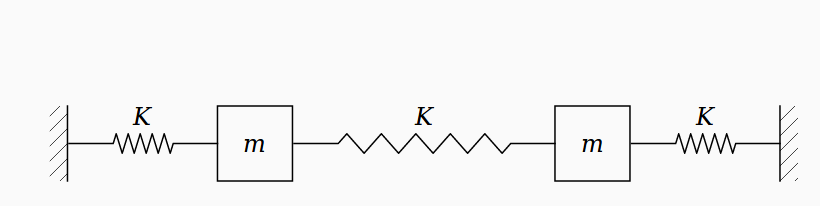
Our system will consist of two blocks, each of mass m, which slide on a frictionless floor. The blocks are connected to fixed walls at each end by a spring of force constant k, and a third spring of the same k connects to the two blocks.
In the figure below, the system is in static equilibrium. The blocks are motionless, and each spring is at its rest length.
Suppose that we displace each block by some small distance away from its equilibrium position. Let's call the displacement of the left-hand block x1, and that of the right-hand block x2.
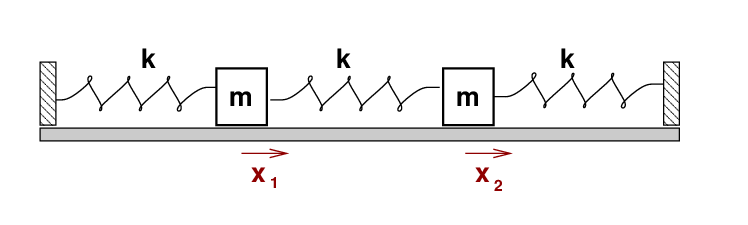
Q: What is the force on each block?
Each block experiences a force from two springs, one on each side. Notice that the force of the middle spring on block 1 must be equal and opposite to its force on block 2.
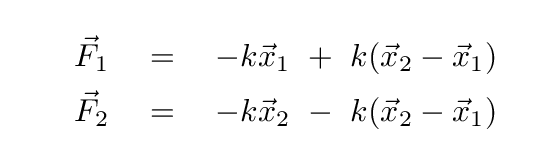
From this point forward, I will stop writing the vector signs, just for simplicity's sake. But we'll have to keep very careful watch on the sign of each term...
Another way to write this is in terms of the second derivative of each block's position with respect to time.
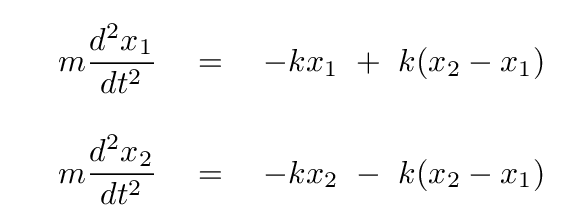
We can put these in a more conventional form for differential equations by moving all the terms to the left-hand side, and by dividing both sides by the mass m of each block.
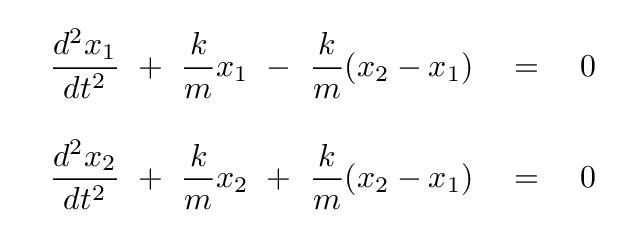
Q: Can you re-arrange the terms in each equation so that all
the x1 and x2 terms are grouped
together?
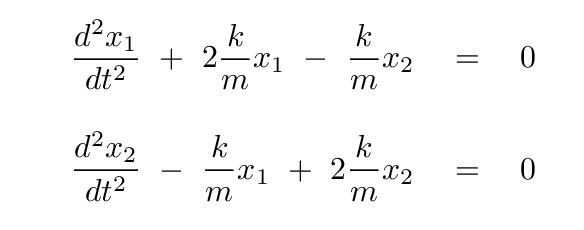
Now, this is ALMOST what we want: each of the two equations above is a second-order differential equation for the position of a block; and in each case, the second derivative of position with respect to time, plus a constant times the first derivative, ALMOST equals zero. But, alas, in each case, there is a term which includes the position of the other block.
Our equations have mixed bits of block 1 and bits of block 2 together. It reminds me of this classic commercial:
Image courtesy of
Reese's Peanut Butter Cups and the 1980s
(or local copy)
How can we handle this complication?
Let's take inspiration from the method of Fourier analysis. There, when given a possibly complicated periodic function, we
Maybe we can do something similar here. Let's just GUESS that there is some linear combination of the variables x1 and x2 -- it could be something like
or
which happens to satisfy our old friend the second-order differential equation
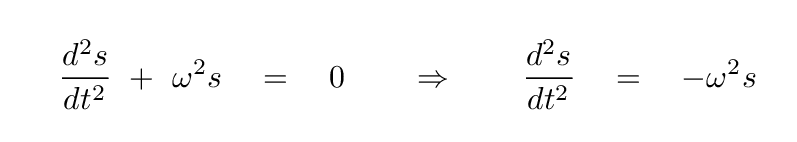
If we do find such a linear combination, then we know how solve the resulting differential equation: that particular combination of x1 and x2 will simply oscillate in SHM.
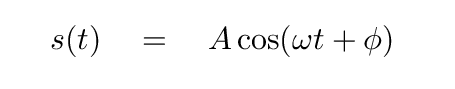
Question Number One is -- what combinations of x1 and x2 should we choose as the equivalent of the "basis functions"? In other words, as the equivalent of sines and cosines in Fourier analysis.
Question Number Two is -- if we find our system already oscillating in some complex way, how can we figure out the right mixture of these special combinations?
In general, finding the combination of variables which yields SHM is a complicated task. We will encounter a technique that works in most situations later, but for today, we can take advantage of the very simple setup ... and symmetry.
Just look at that picture for a moment, then answer these questions:
Q: What happens to the middle spring if x1 = 1 cm and x2 = 0 cm ? Q: What happens to the middle spring if x1 = 0 cm and x2 = 1 cm ? Q: What happens to the middle spring if x1 = 1 cm and x2 = 1 cm ?
Hmmm. If both blocks move exactly the same distance, in the same direction, then the middle spring remains at its rest length; it won't exert any forces on the blocks.
Thanks to Erik Cheever at Swarithmore , you can watch an animation of this system. Go to
and scroll down one-third of the page to "Set Initial Conditions." Try it and see what happens.
One way to reach this linear combination is to add together the two differential equations:
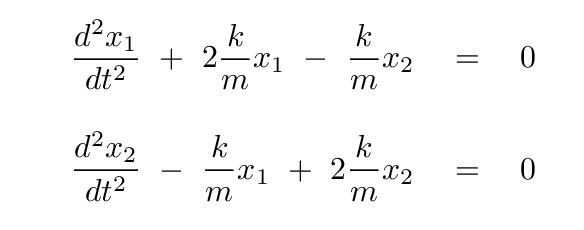
Q: Add these two equations, and then group together terms
with equal amounts of x1 and x2.
You should end up with
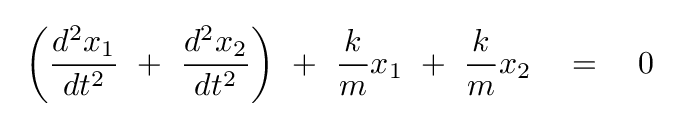
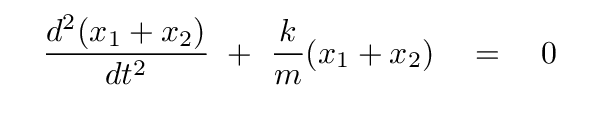
Great! If we define a new coordinate variable s1
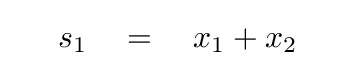
then the two differential equations turn into a single equation which should look very very familiar.
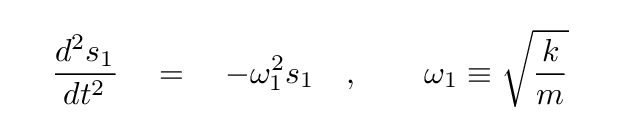
You can use Erik Cheever's animation to watch the system move in this mode. Note
It turns out that combinations which lead to both objects moving at the SAME frequency will be good ones to use as the basis for building more complicated motions. The term normal modes is sometimes applied to such combinations.
We have found that the sum of the two ordinary coordinates
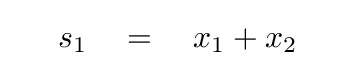
yields one of the normal modes of this system. But are there any other combinations which will also yield normal modes?
Well, watch what happens if, instead of displacing both blocks 1 cm to the right, we displace the two blocks 1 cm in OPPOSITE DIRECTIONS. Once again, go to Erik Cheever's page , but this time, set the initial conditions to -1 and 1.
Aha! This time, the middle spring certainly does exert forces: it expands and contracts, expands and contracts, exactly in time with the two springs attached to the walls. The distance between the blocks, (x2 - x1), is constantly changing. Maybe we should consider that difference as our next linear combination:
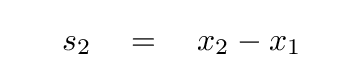
One way to achieve this combination is to SUBTRACT one differential equation from the other.
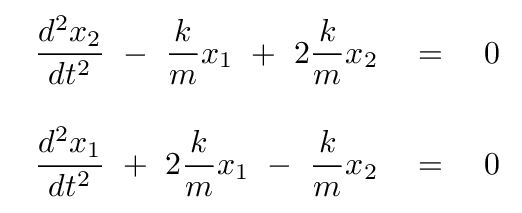
Q: Subtract these two equations, and then group together terms
with equal amounts of x1 and x2.
You should end up with
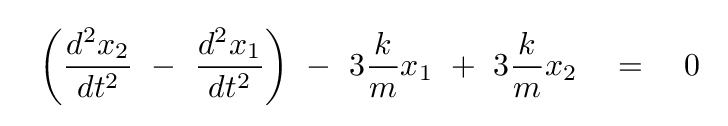
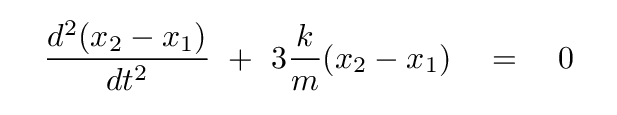
Q: What is the frequency of this mode?
Right. If we monitor the combination
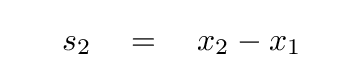
we will find that it undergoes SHM
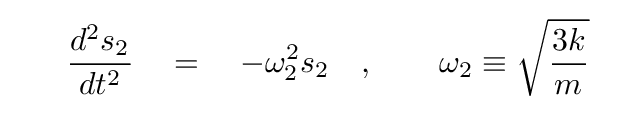
But notice the differences. The positive combination (x1 + x2) yields a mode in which the two blocks oscillate
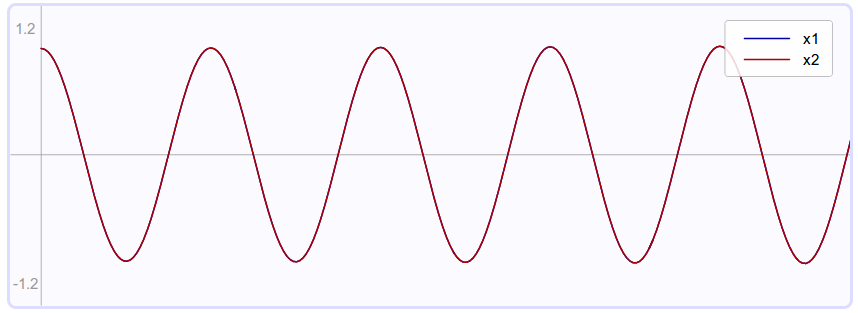
Taken from
Erik Cheever's page with initial displacements +1, +1
The negative combination (x2 - x1) yields a mode in which the two blocks oscillate
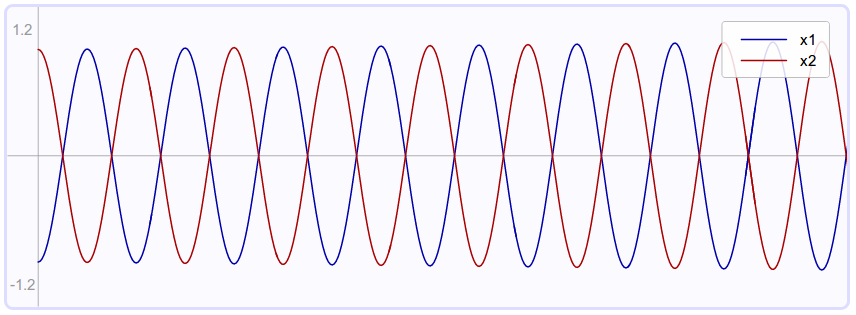
Taken from
Erik Cheever's page with initial displacements -1, +1
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.