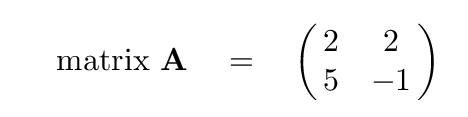
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Before we get to the real topic of today's lecture, let's warm up by reviewing a bit of matrix arithmetic.
Suppose we are given a 2x2 matrix
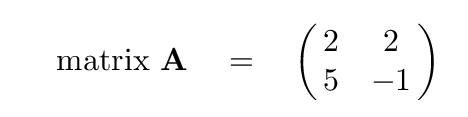
and a 1x2 vector
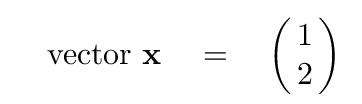
What is the result of multiplying the matrix by this vector?
Q: What is the result of this multiplication?
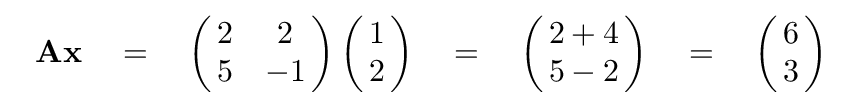
Okay. Now, let's look at the input vector x and the output of the calculation. Do they share any similarities?
Doesn't look like it to me. Just two unrelated 1x2 vectors. Hmph. Not very interesting.
Well, maybe it will be more interesting if we pick a different input vector. How about this one?
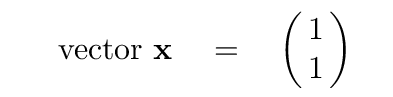
Q: What is the result of multiplying the matrix A by this vector?
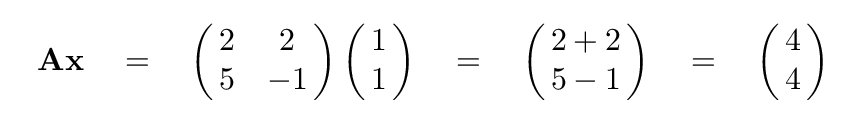
Hmmm. If we compare the input vector x to THIS result ...
Q: Do you see any similarities this time?
I see one: the result is exactly 4 times the input vector.
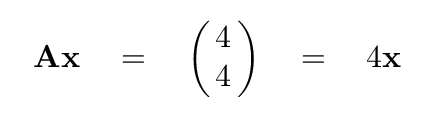
That's noteworthy. Is it a coincidence? Are there any other vectors which might also yield a result which is just a simple multiple of themselves?
Try this one:
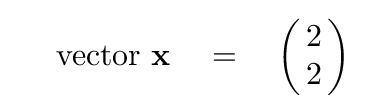
Q: What is the result of matrix A multiplied by this vector?
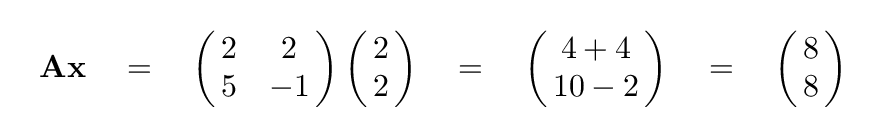
Hey! That's just a factor of 4 times the input vector -- again.
It turns out to be VERY useful, in a number of scientific and mathematical situations, to find the vector x which, when multiplied by some matrix A, will yield a multiple of itself.
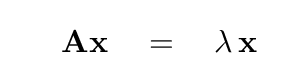
It is so useful that special terms have been coined to describe these quantities.
One of those situations is the one we are studying right now: the motion of coupled oscillators. We are going to want to know the eigenvectors and eigenvalues for particular systems, so we ought to learn how to find them.
And so -- let's see how one can find the eigenvalues and eigenvectors associated with some matrix. We'll use a simple 2x2 matrix for convenience. In fact, let's use this particular matrix:
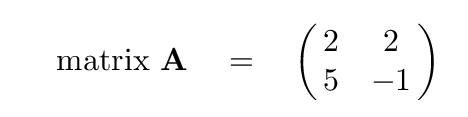
Our goal is to find vector(s) x and scalar(s) λ which will satisfy this equation:
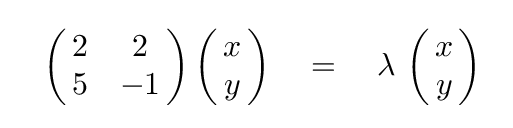
Let's do it the old-fashioned way. Write out the two equations for the components.
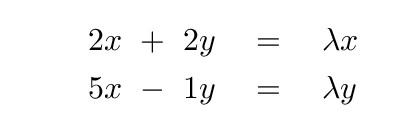
Two equations, and three unknowns? Don't worry -- we can handle it. First, eliminate one of the vector components; I'll choose to get rid of y.
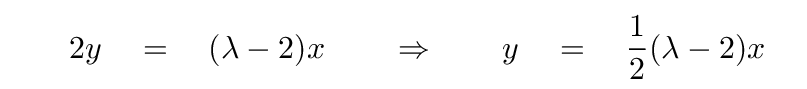
Substitute this value for y in the other equation.
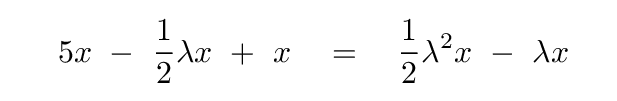
Why, how convenient! Every single term in this equation has a factor of x in it. As long as we promise not to let x = 0, we can divide by sides by x -- which will leave us with just a single unknown quantity:
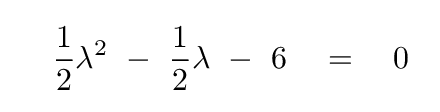
Looks like a quadratic equation. We could solve for the values of λ right now, but some people prefer to avoid fractions in their quadratic terms. To make them happy, let's multiply by 2.
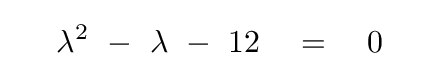
This quadratic equation we find in the middle of our eigen-seeking procedure is called the characteristic equation.
Q: What are the values of λ which satisfy this equation?
The roots of this equation yield the eigenvalues λ
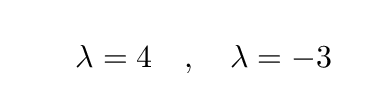
Now, each of these eigenvalues has an eigenvector associated with it. How do we find the eigenvector for some eigenvalue? Just plug the eigenvalue into the matrix multiplication.
For example, if we pick eigenvalue λ = 4, then the matrix multiplication becomes
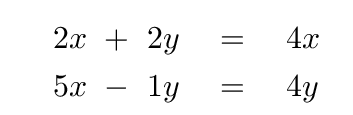
Solve either equation for y in terms of x -- it will be the same for both equations.
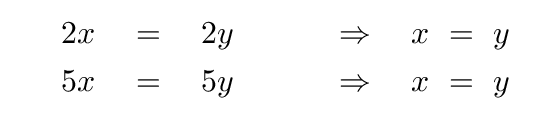
The answer will show you that there are an infinite number of eigenvectors associated with a single eigenvalue ... but they are all just multiples of each other.
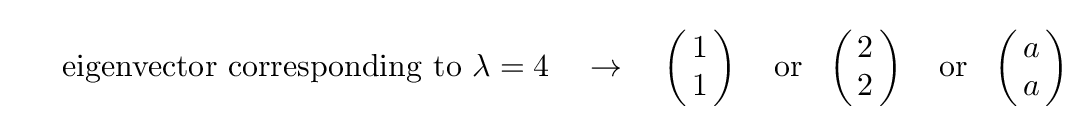
What's really important for an eigenvector is the RELATIVE AMOUNT of each component: how many parts of the first component for each part of the second? In the case above, the mixture is 1 part x and 1 part y.
Okay, your turn:
Q: What is the eigenvector corresponding to the eigenvalue λ = -3?
You should find
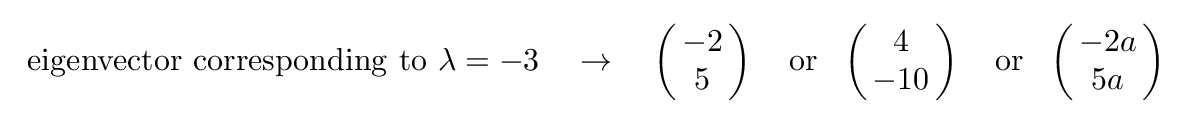
What DOES all this eigen-stuff have to do with the motion of two coupled oscillators?
Quite a bit. Recall, please, the equations we derived a short time ago describing the forces on two identical blocks which are connected by three identical springs.
Well, suppose that we re-arrange the terms in this equation just a bit, putting the derivatives over on the right-hand side.
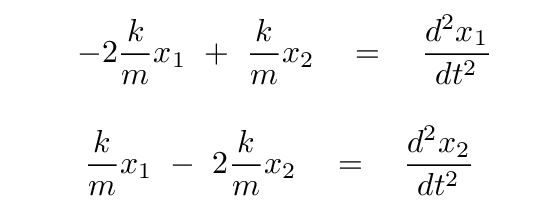
Doesn't this look a bit like a matrix equation? In particular, like THIS matrix equation?
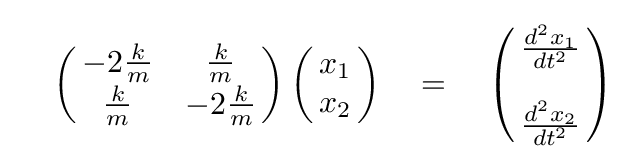
Now, this next step is the crucial one. What we need to do is to combine the the real-life positions of the blocks, x1 and x2, in just the right mix. Let us define a new coordinate s which has exactly the right combination, mixing "a" parts of x1 with "b" parts of x2.
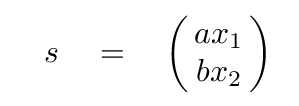
If we pick just the right mixture, we'll end up with a situation in which the second derivative with respect to time of this new coordinate is
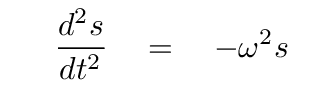
In that case, our equations connecting forces and accelerations can be written
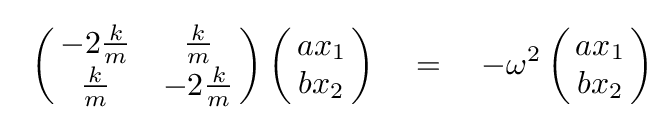
And that is simply the equation for the eigenvector s and eigenvalue λ = - ω2 corresponding to a matrix A.
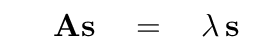
How to find this "just right" mixture of the block coordinates? All we have to do is to find the eigenvectors and eigenvalues of the following matrix equation.
Let's do it!
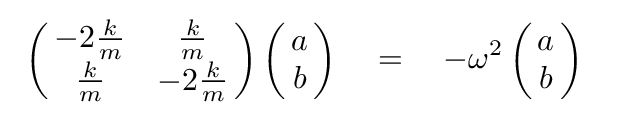
It will make things a bit easier if we move all the terms to the left-hand side.
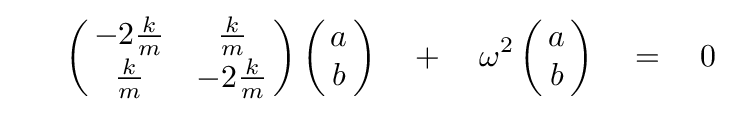
Write down the two equations which result from performing
this matrix multiplication.
You should get
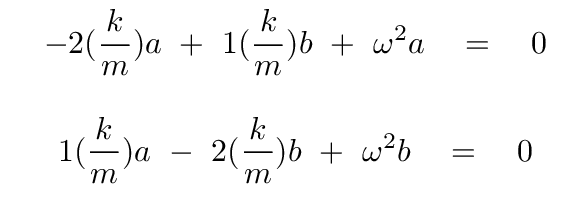
Just as we did earlier, we can solve these two equations for three unknowns to end up with the eigenvectors and eigenvalues of this equation.
Use the first equation to solve for b in terms of a.
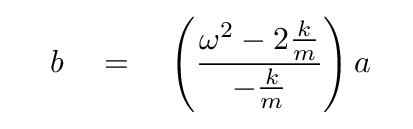
Now plug this into the second equation ...
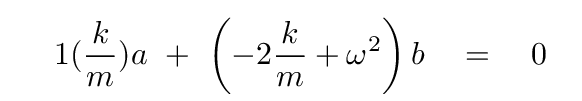
... to get
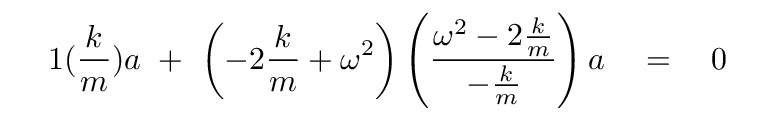
Now, I know that looks bad, but actually, it simplifies quite a bit. Divide both sides by a, and after some algebra, you should find
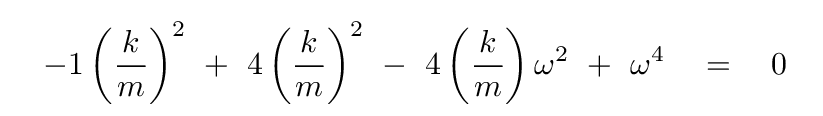
Hmmm. This is sort of like a quadratic equation, but the variable ω is raised to the fourth power. That's annoying. Let's make it more conventional by defining
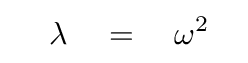
With this notation, the equation really is a simple quadratic
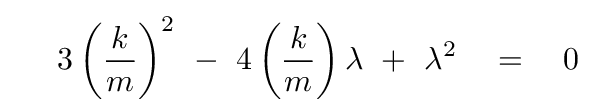
Q: What are the roots of this equation?
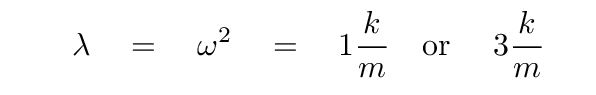
And so we see that the eigenvalues correspond to the frequencies of the normal modes.
We're almost there now. Let's pick one of these eigenvalues, ω1 = √(k/m), and find its corresponding eigenvector.
To find the eigenvector, we insert an eigenvalue into those equations we derived earlier:
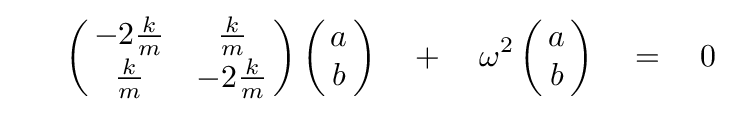
which yields
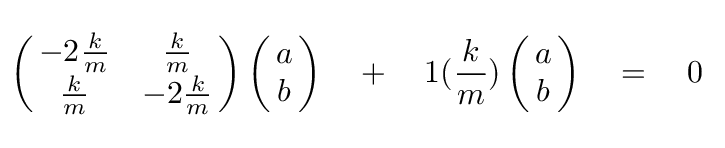
Now, perform the matrix multiplication, and you'll end up with two equations:
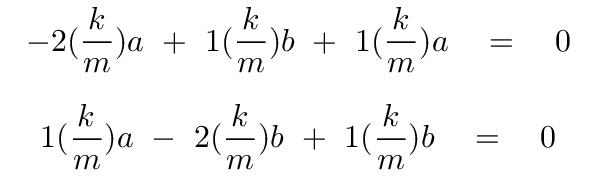
Q: Solve either of these equations for the variable a in terms of b
Each equation turns into
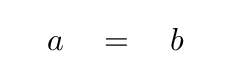
which means that
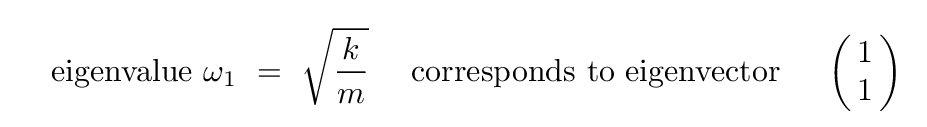
And the eigenvector tells us how to mix together the physical coordinates of the blocks x1 and x2 in order to find a combination which exhibits simple harmonic motion, with a frequency ω = √(k/m).
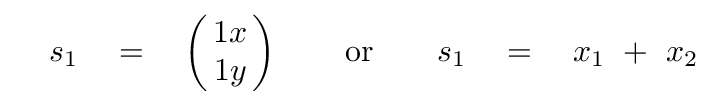
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.