
 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
We're in the middle of figuring out a way to describe the motion of a pair of coupled oscillators. Today, we'll take the process to its end.
As you may recall from last time, our system consists of two blocks, each of mass m, which slide on a frictionless floor. The blocks are connected to fixed walls at each end by a spring of force constant k, and a third spring of the same k connects to the two blocks.

We wrote down two equations, one for each block, which describe the forces acting on each block and the resulting acceleration:
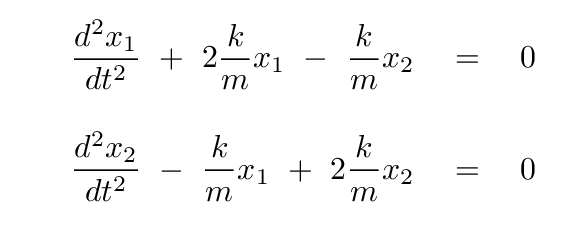
The trouble with these equations is that they contain a MIXTURE of variables: the second derivative for each block depends not only on its own position, but also on the position of the other block.
Our plan to deal with this issue was to re-arrange the variables. By creating just the right mixture of x1 and x2, we might end up with a simpler second-order differential equation, in terms of just one variable. We used symmetry and some intuition to GUESS that these combinations might work:

And it turned out that they did work. We found that these combinations of the two blocks exhibit simple harmonic motion, but with different frequencies.
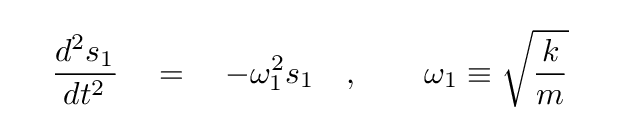
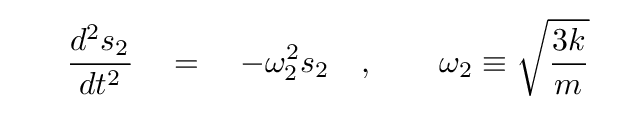
There are special terms for these special combinations:
If we express the state of two blocks in terms of one of these new coordinates, it varies in simple harmonic motion:
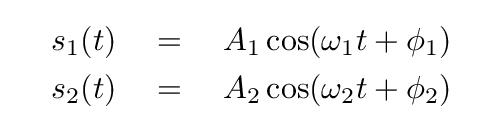
Why should we give special names to these particular modes of oscillation? The answer is -- just as one can break up ANY complicated periodic function into a sum of sine and cosine functions, one can break up ANY complicated motion of the two-block system into a sum of these special modes. In other words, these normal modes will serve as the BASIS FUNCTIONS for the two-block, three-spring system.
But those two equations, for s1(t) and s2(t), have four constants of integration:
The answer is just the same as it was when we were investigating SHM and damped harmonic motion: look at the initial conditions. We have four constants to determine, so we need four initial values. The positions and velocities of the blocks at time t = 0 will do just fine.
At time t = 0,
x1 = 0
x2 = +L
v1 = 0
v2 = 0
Given those initial values, we can, first of all, compute the positions s1(0) and s2(0), and the velocities ds1/dt(0) and ds2/dt(0).
Q: What are the values of these quantities at time t = 0?
Yes, exactly.
s1 = L
s2 = L
ds1/dt = 0
ds2/dt = 0
With this information, we can figure out the values of the coefficients in
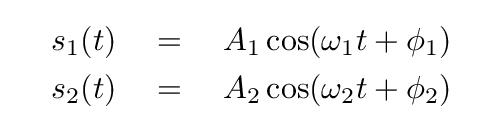
Q: What are the values of A1 and φ1? Q: What are the values of A2 and φ2?
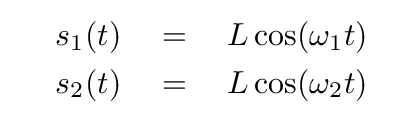
And so, if we plot the normal coordinates as a function of time, we see simple harmonic motion. One mode oscillates faster than the other.

Well, great. If someone asks us "What is the current value of the sum of the positions of the two blocks?" we can provide an answer.
But what if someone asks us "What is the current position of the left-hand block?" The equations above don't tell us that, do they?
Q: Is there any way to figure out the position of the
left-hand block at an arbitrary time?
If we go back to the definitions of our "normal coordinates", maybe we CAN find a way to isolate the position of the left-hand block, x1.

Suppose that we subtract the second equation from the first equation. We will end up with

At this point, we can write x1 all by itself as
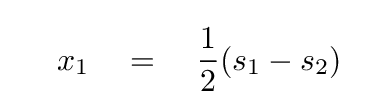
In a similar manner, one can derive
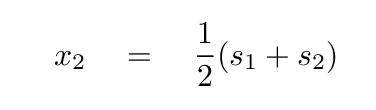
Well, we're almost to the finish line. In order to figure out the position of the left-hand block, x1, at any time, we can insert our expressions for s1(t) and s2(t) into the above equation.
Write an equation for x1(t) which contains
terms like L, k, m.
Write an equation for x2(t) which contains
terms like L, k, m.
You should end up with
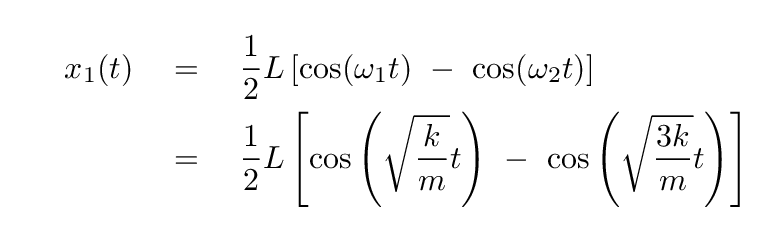

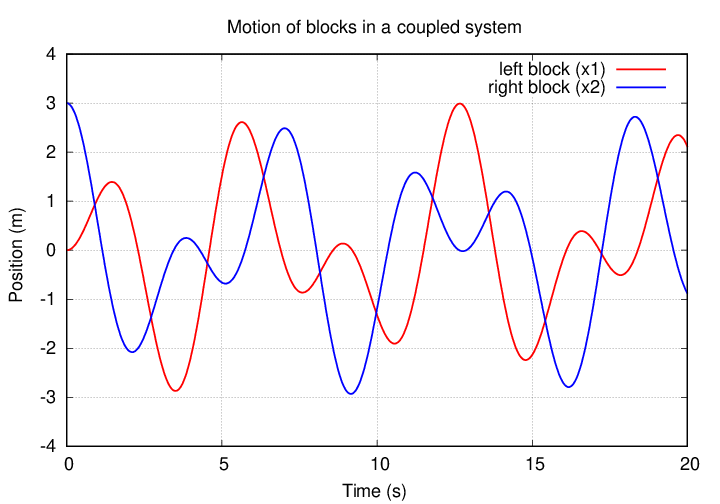
So, the motions of the blocks aren't SIMPLE harmonic motion; the amplitudes of their motions appear to change over time.
But the values of the combined quantities s1 and s2 DO exhibit simple harmonic motion.

A summary of the process for solving this system with coupled oscillators is
Fred sets up the same old system of blocks and springs.

This time, however, he gives it a different set of initial conditions.
At time t = 0,
x1 = -L
x2 = +2L
v1 = +W
v2 = 0
The same old combinations we used earlier to define new coordinates s1 and s2 will work here again, and so the general form of the equations for s1(t) and s2(t) will be the same again; but the values of the coefficients will be different.
Q: Can you figure out the values of the coefficients
A1 and φ1,
A2 and φ2?
Let's make things more concrete by putting some numbers in place of the variables:
Write equations giving s1(t) and s2(t),
showing the numerical value and units of all terms.
The result should look something like this:

Now it should be easy to figure out the position of each block as a function of time.
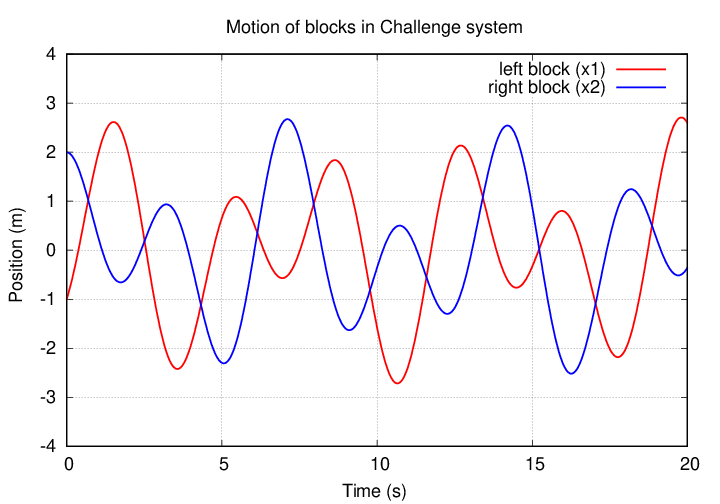
Q: Can you write equations for x1(t) and x2(t),
providing numerical values and units for all terms?
The result should look something like this:
 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.