
Image courtesy of NASA/JHUAPL/SwRI
 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Contents
On January 19, 2006, NASA launched the New Horizons probe from Cape Canaveral. The main goal of this mission was to fly past the mysterious world Pluto and acquire pictures and other data of Pluto and its moon Charon.
The spacecraft took quite a while to get there, but when it did -- on July 14, 2015 -- its instruments worked perfectly. Some of the most beautiful images, like the one below, were taken by the LORRI (LOng Range Reconnaisance Imager) instrument.

Image courtesy of
NASA/JHUAPL/SwRI
LORRI is really more than a camera -- it's a telescope which focuses light onto a detector. Not a small telescope, either, but a 208-mm, f/12.6 Ritchey-Chretien design which yields a field of view about 0.29 x 0.29 degrees.

Image courtesy of
Spaceflight 101

Image courtesy of
JHU/APL
After the Pluto and Arrakoth encounters were over, the New Horizons team decided to use LORRI as an ordinary telescope, and take pictures of a star. Well, this isn't quite an ordinary telescope; it has one feature that makes it unique among all the telescopes of the world: its location.
Let's take a look at the journey of the spacecraft since its launch, on Jan 19, 2006.
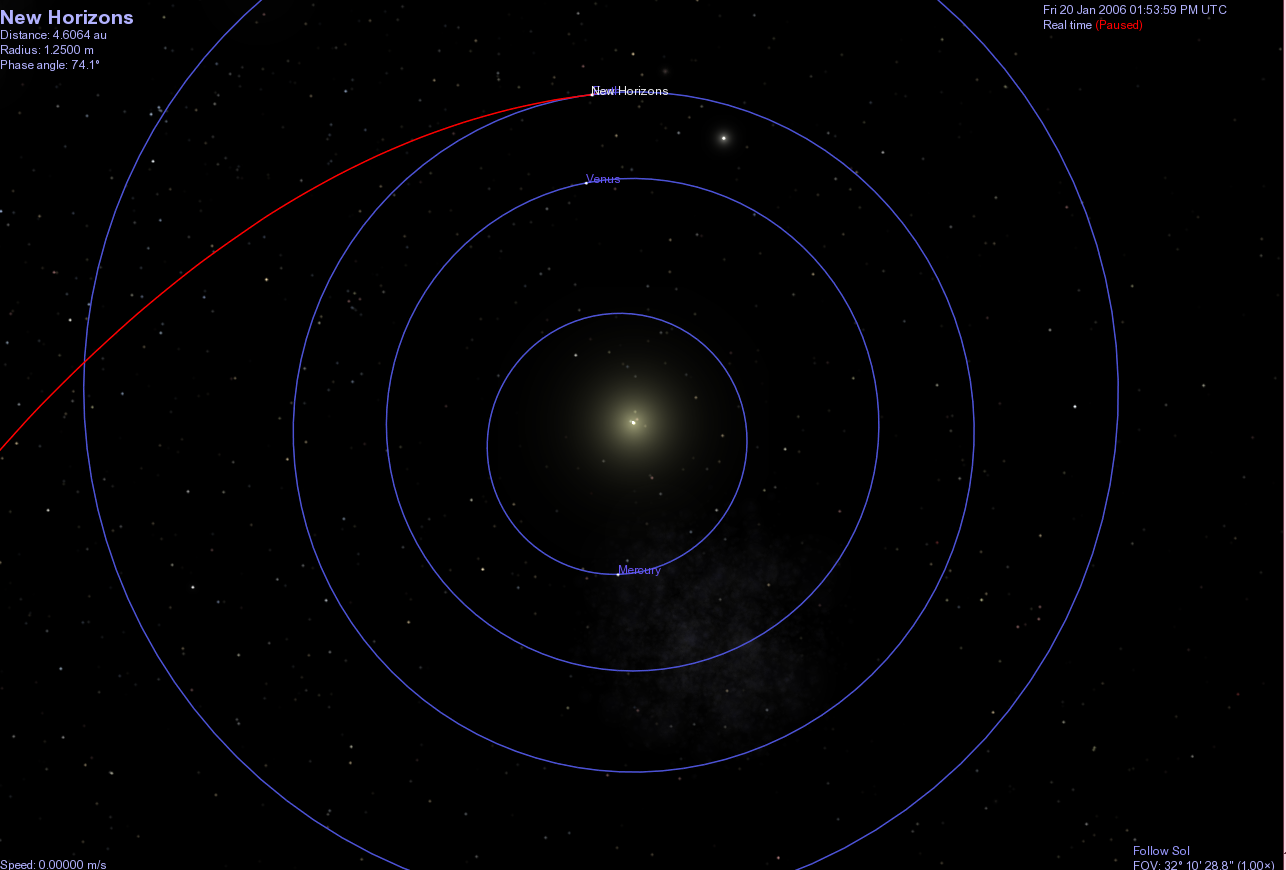
After just three months, it had already moved outward past the orbit of Mars.
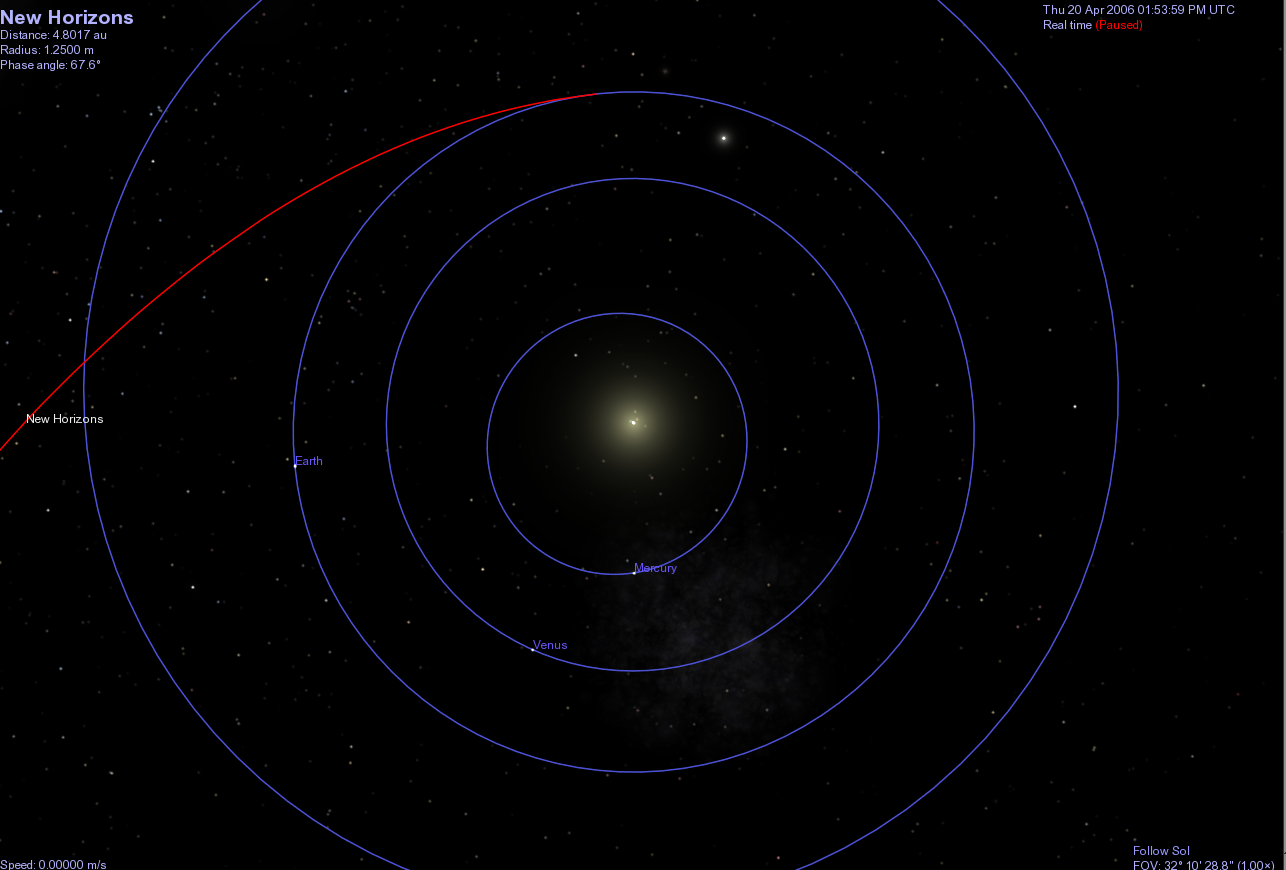
A little over one year after launch, the spacecraft flew past Jupiter. The gravitational force of the King of Planets bent the trajectory of the probe slightly and gave it a boost of speed.
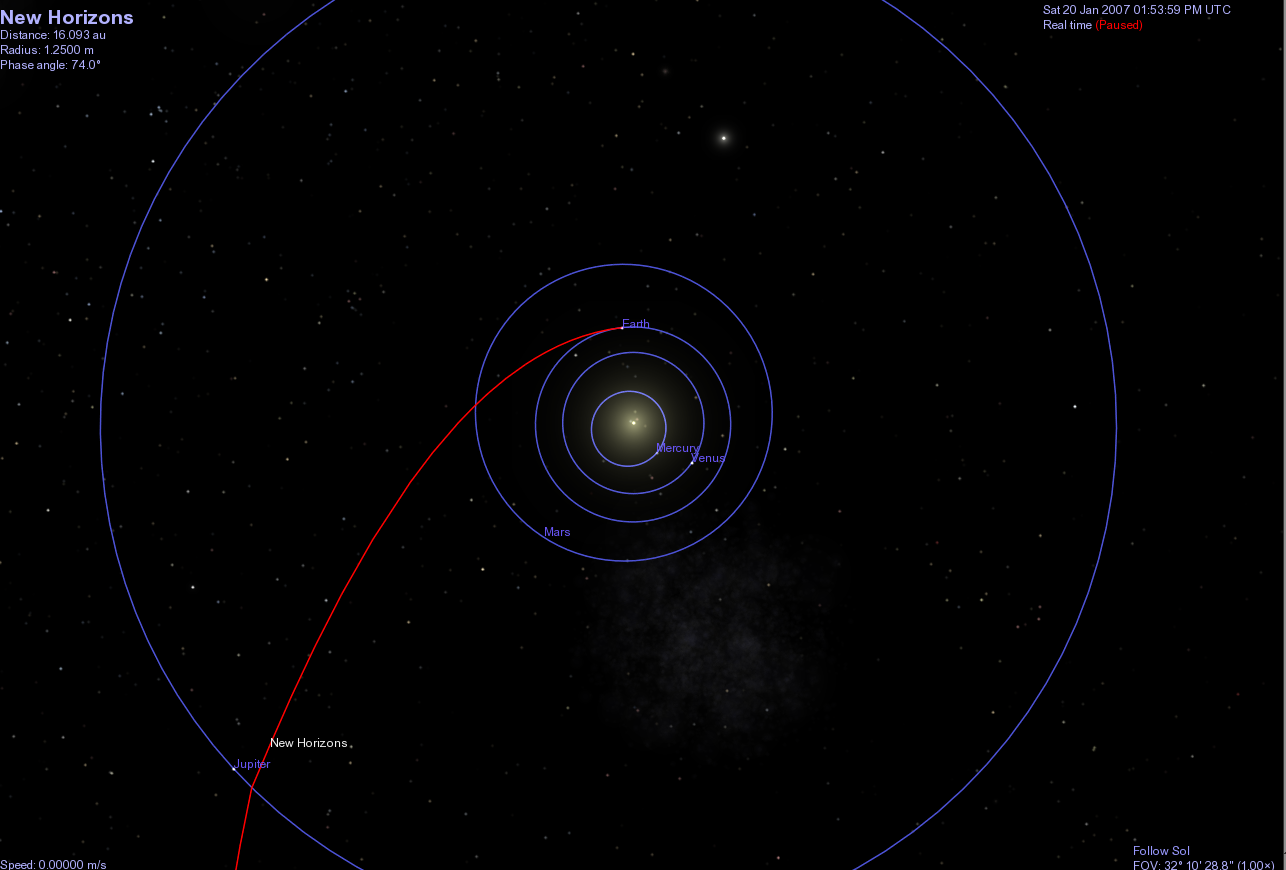
On Apr 23, 2020, the spacecraft was still zooming away from the Sun, having passed the orbits of Neptune and Pluto. Because it is so far from the Sun and the planets, the gravitational forces on it are negligible, and it is now travelling in almost a perfectly straight line.

In order to show Earth and New Horizons clearly in the same diagram, let me rotate the picture by 90 degrees.
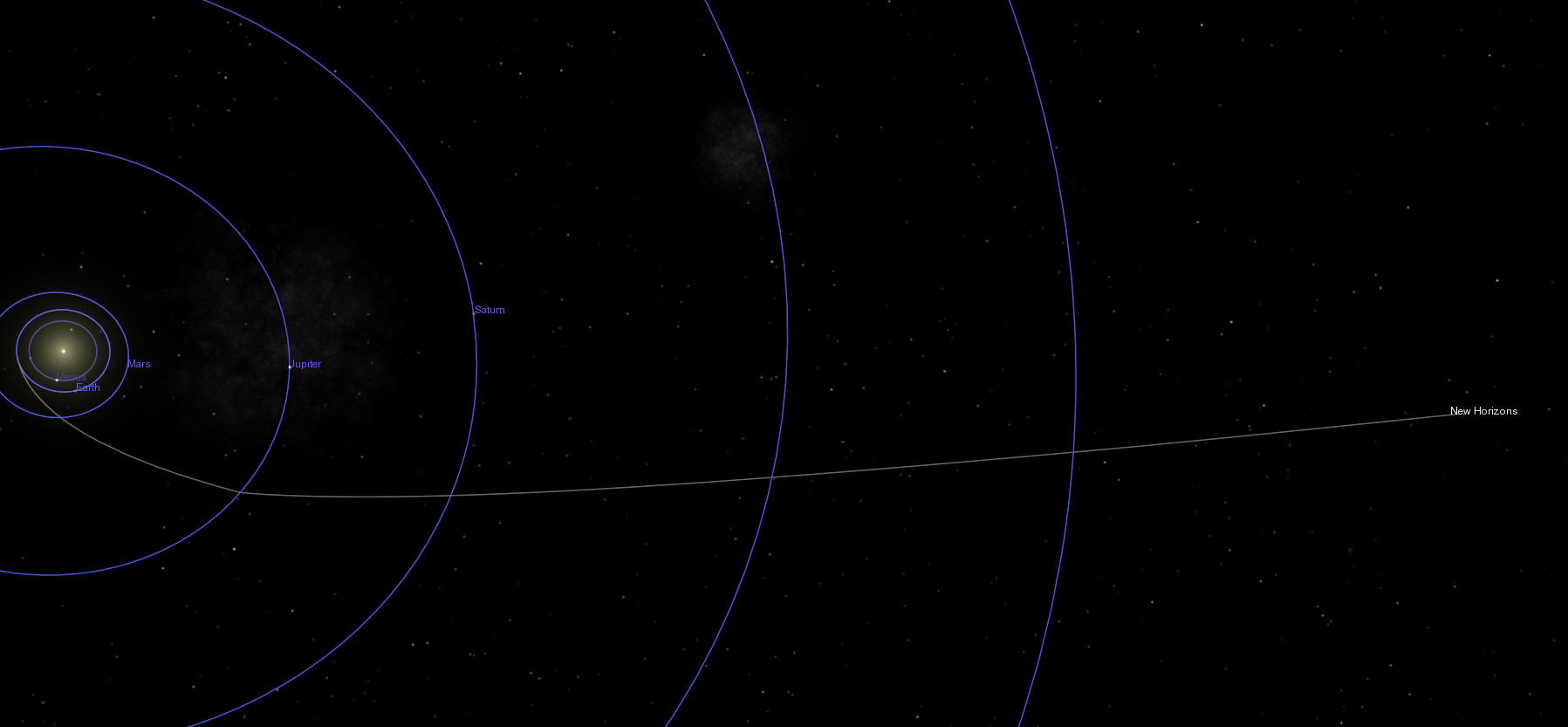
So, on Apr 23, 2020, New Horizons was very far from the Earth. How far? About 46.848 Astronomical Units (AU), or 46.848 times the distance between the Earth and the Sun. You can look up the distance for any date you wish at the JPL Horizons system.
The star Wolf 359 got its name from a catalog of stars with high proper motions compiled between 1919 and 1931 by the German astronomer Max Wolf. This particular star lies in the constellation of Leo, below the lion's torso. On the night of Apr 23, 2020, it was nearly due south as seen from Rochester in the early evening.
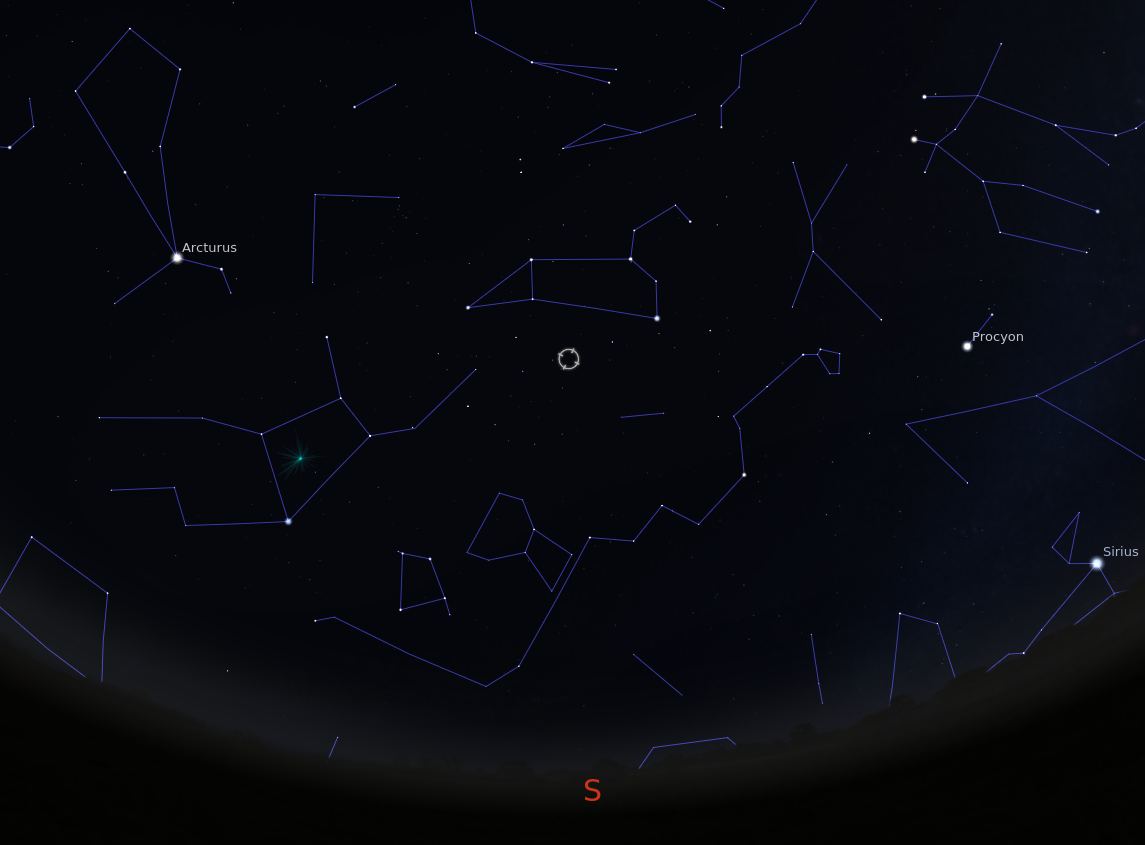
If we zoom into to a small box, about one-third of a degree on a side, we see several groups of moderately bright stars; I've drawn lines between some of them to make "mini-constellations" for aid in orientation. There's also a faint spiral galaxy in the lower-left (south-eastern) corner of the region.

The red cross marks where Wolf 359 would be in 2020. Since this chart is based on a photograph taken in the 1950s, the star was not at this location; it's actually hiding elsewhere.
On the night of Apr 18/19, 2020, I took an image of this region of the sky at the RIT Observatory. The orientation is the same (North up, East left), as is the size (about 20 arcminutes on a side). Can you find the three "mini-constellations?"

A few nights later, on Apr 23, 2020, the New Horizons spacecraft took its own images of this area with LORRI. The picture below is the median of the three images made available to the public at the New Horizons parallax images webpage. As you can see, the background is a bit messy, and the pixels are much larger than those in the RIT image. But the "mini-constellations" are still there -- right?

We can "blink" these two images in order to find the one star which appears to "jump" from one location to another. That star is Wolf 359. Can you find it?

Aha! We see a clear shift in the position of Wolf 359 in these two images. Why? The answer lies in this diagram showing the location of New Horizons on Apr 23, 2020:
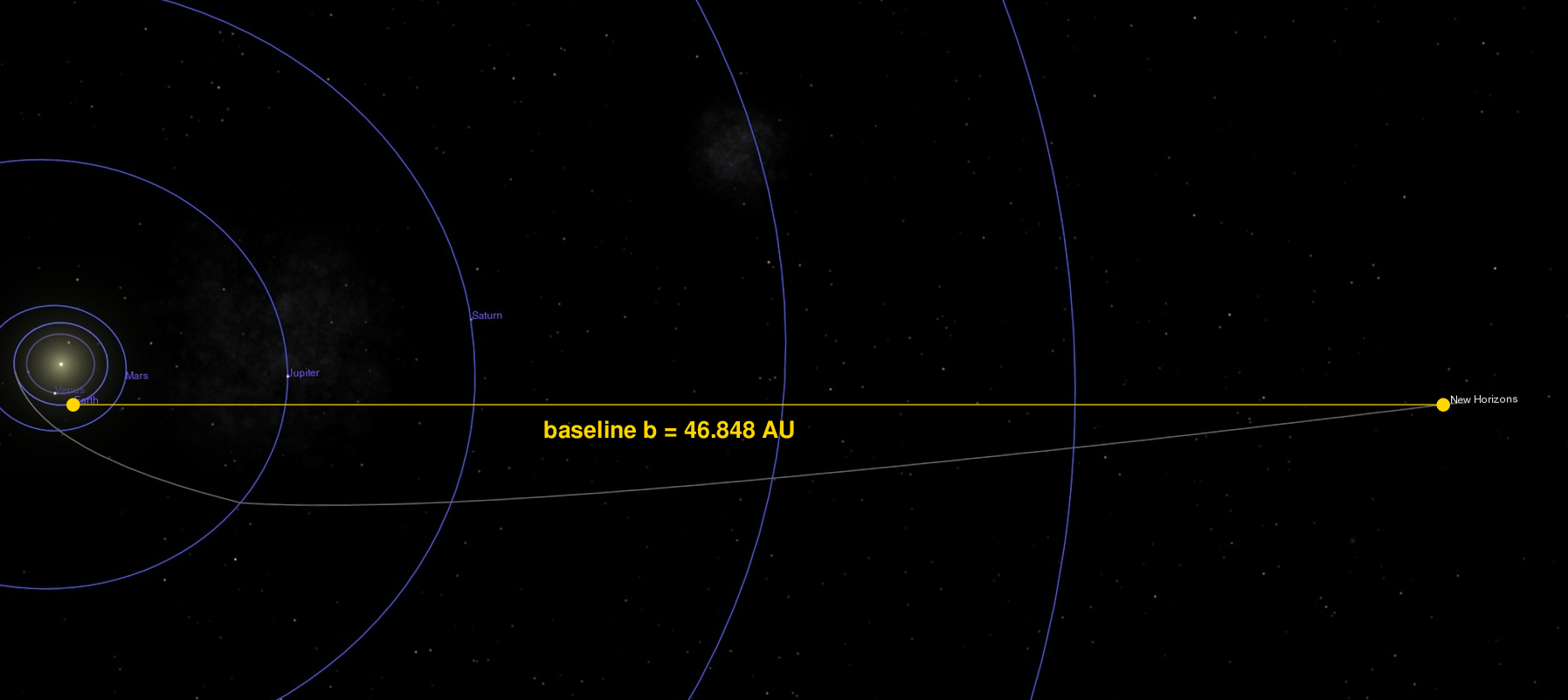
Since telescopes on New Horizon and the Earth are separated by a very large distance (about 46 AU), when they look at the same nearby star, they see it in a very slightly different position relative to more distant stars.
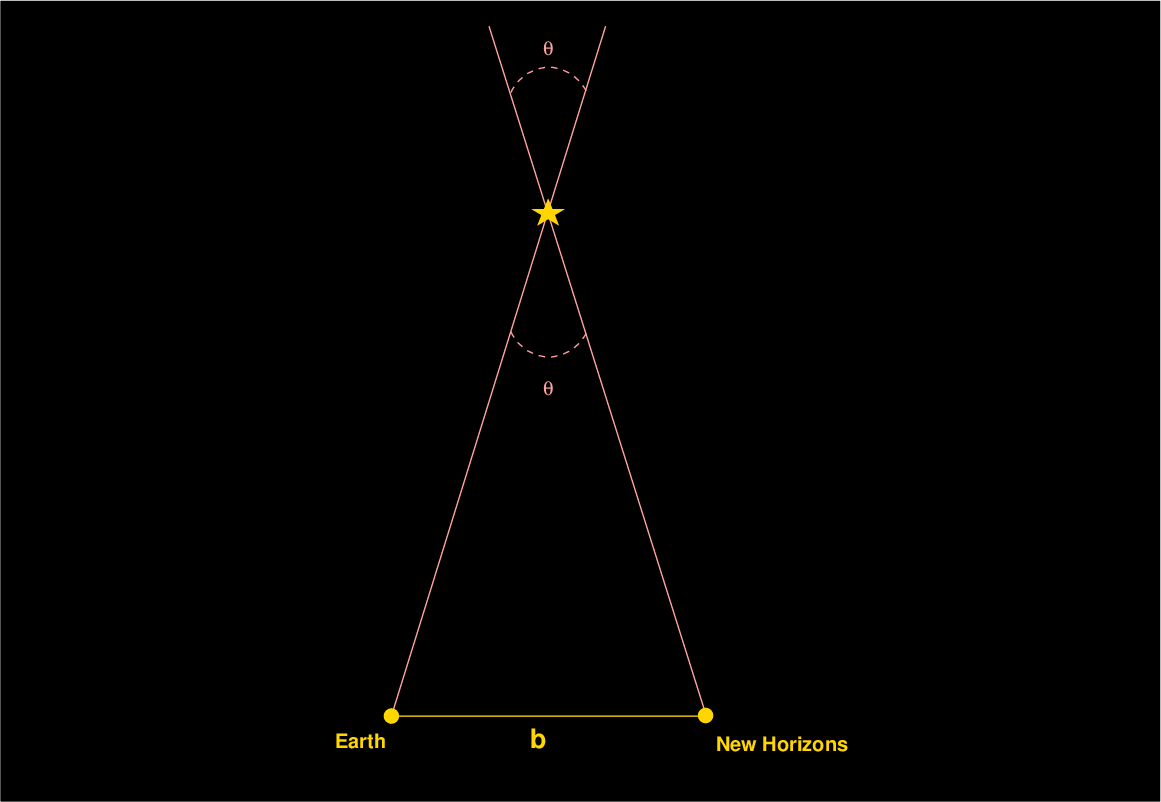
This shift in the apparent position of a nearby object relative to distant ones is called parallax. If we can measure the size of the shift, the angle denoted by θ in the diagram above, then we can determine the distance to the star.
In order to find the angle θ, we need to indulge in a bit of mathematics. First, we look in the Gaia DR2 catalog for a list of stars in this region of the sky with known positions. There are quite a few -- I've marked their positions with red boxes in the chart below.

Next, we pick one of the images; let's start with the New Horizons picture. We measure the positions of each star we can detect in the image, yielding a set of (x, y) values in pixels. Then we compare those to the positions of the same stars from the catalog, which have units of (RA, Dec) in decimal degrees. If we can match up the stars from the image (x, y) with the stars from the catalog (RA, Dec), we can figure out an equation which converts the pixel (x, y) values into calibrated (RA, Dec) positions. I used a bit of software I wrote to do the job.
In this case, there were 18 stars in the catalog which matched stars in the New Horizons image, yielding a transformation with typical residuals of about 0.3 arcseconds. Using that transformation, I computed the position of Wolf 359, as seen by New Horizons:
observer RA Dec --------------------------------------------------------------- New Horizons 164.094354 7.001044 ---------------------------------------------------------------
Okay, time for measuring the position of Wolf 359 in the RIT images. Due to bad weather, I wasn't able to observe the star at exactly the same time as New Horizons, on April 23. However, I was able to make a series of measurements on two nights just before that date, and one night a short time afterward. Interpolating between the positions on those dates, I determined that at the time (Julian Date 2458962.82310) that New Horizons took its image, the star was at the following position as seen from RIT:
observer RA (α) Dec (δ) --------------------------------------------------------------- New Horizons 164.094354 7.001044 RIT 164.0984279 6.9995173 ---------------------------------------------------------------
Right. Now that we have two positions on the sky, each with a Right Ascension (α) and Declination (δ) component, we can use a bit of spherical trignometry to determine the angle θ between the positions. Note that the formula below yields the cosine of the angle θ; in order to determine θ itself, we need to take the inverse cosine of this result.
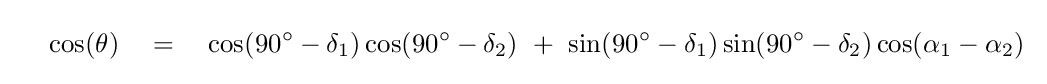
A few moments with a calculator reveal that the parallax angle of Wolf 359, as seen from RIT and from New Horizons, is
parallax angle θ = 14.87 arcseconds
= 0.004131 degrees
So, we know the size of the parallax angle. It ought to be a simple matter of geometry now in order to determine the distance to the star, right? We just cut our angle in half to create a right triangle,
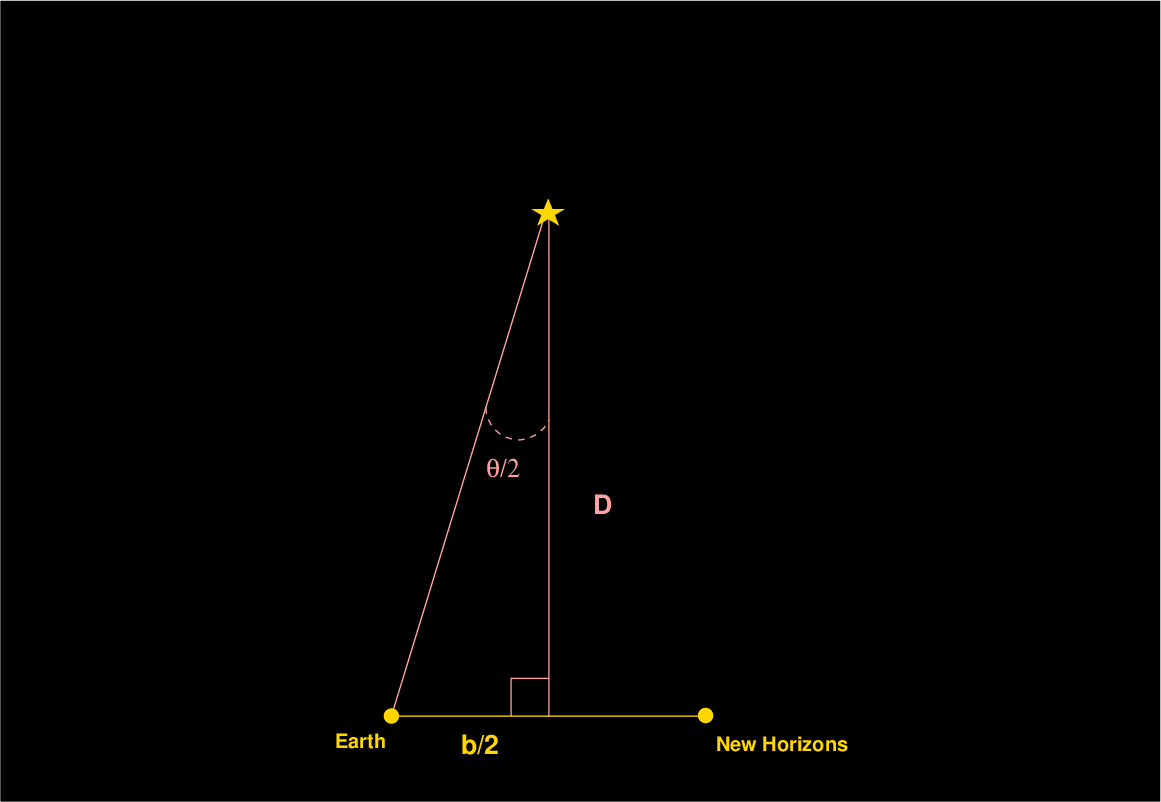
and then compute
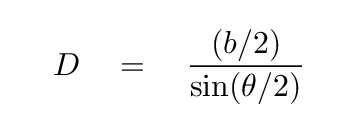
Well, there's just one problem: in this simple arrangement, the direction to Wolf 359 is exactly perpendicular to the baseline between the Earth and New Horizons. But in real life, it wasn't -- alas.
We can use the JPL Horizons system to tell us the exact location of New Horizons on Apr 23, 2020, as seen from RIT. If we compare it to the location of Wolf 359 at the same time, as seen from RIT, we find:
as seen from RIT
object RA (α) Dec (δ)
---------------------------------------------------------------
New Horizons 289.12108 -20.28306
Wolf 359 164.0984279 6.9995173
---------------------------------------------------------------
Are these two directions perpendicular? In order to find out, we can use (again) that same trigonometric formula; this time, we'll use it to compute the angle γ between New Horizons and Wolf 359, as seen from RIT.
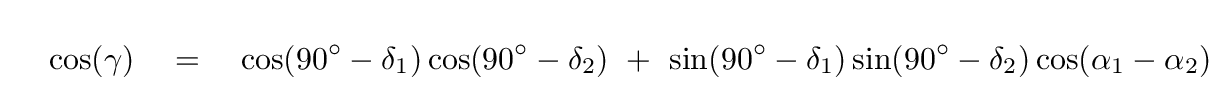
In this case, we find that the angle γ is NOT 90 degrees, but in fact somewhat larger:
angle between Wolf 359 and New Horizons γ = 125.20799 degrees
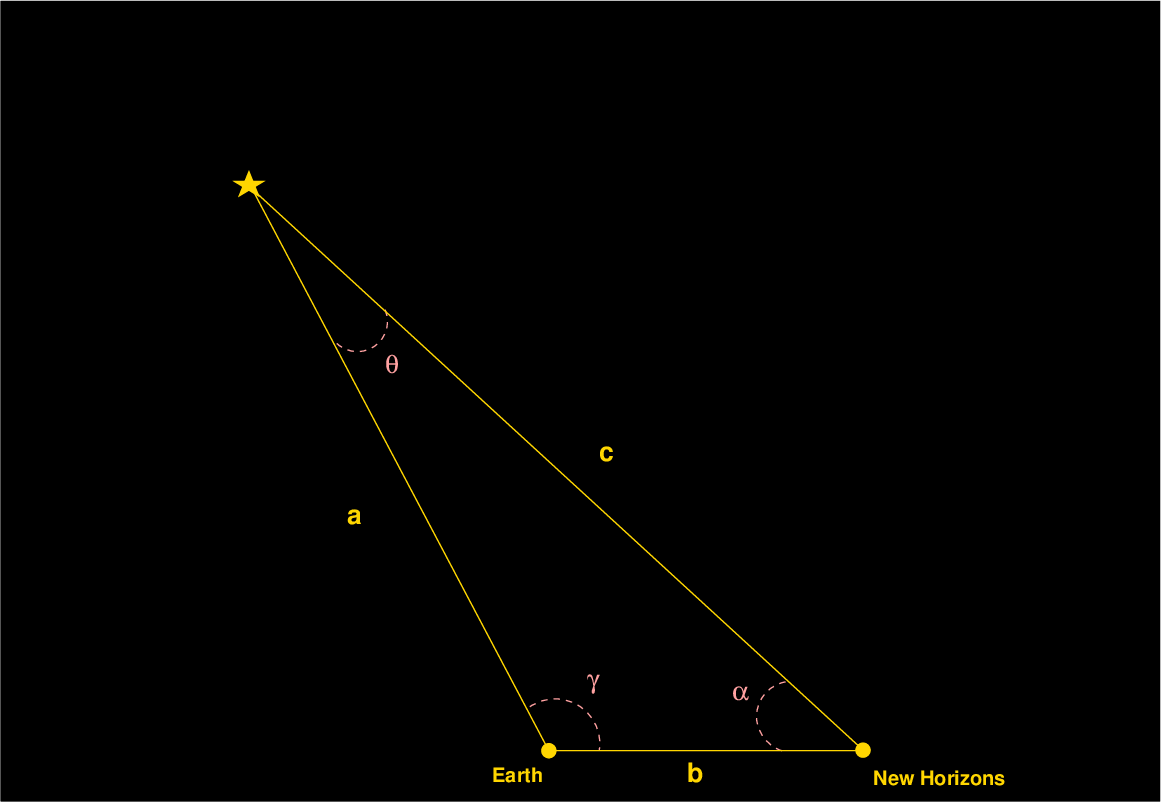
Rats. Our observations don't sit on a nice right triangle, but instead on a rather slanted one. Is there any way to figure out the distance a from Earth to Wolf 359, using a triangle like this?
The answer, fortunately, is still "yes." One method is to use the Law of Sines, which you may recall from some old geometry class. It states that the ratio of the sine of each angle in a triangle to the length of the opposite side is the same. In our diagram above, that means
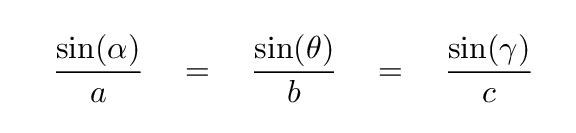
You may also recall from that same geometry class that the sum of all the angles in a triangle must be 180 degrees. We know both the parallax angle θ (which is very small) and the angle γ (which is pretty big), so we can calculate the value of the angle α:
α = 180 - (0.004131 + 125.20799)
= 54.78788 degrees
Phew. We're almost there. The last step is a bit of algebra, to re-arrange the first two pieces of the formula above in order to solve for the distance a.
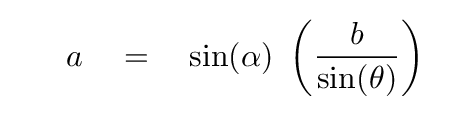
We know all the values on the right-hand side:
The resulting distance a between Earth and Wolf 359 turns out to be roughly 531,000 AU. In my own calculations, in which I tried to account for uncertainties in all the measurements, I ended up with
my distance to Wolf 359 = 531,000 +/- 15,000 AU
= 2.57 +/- 0.07 pc
Now, is this distance correct? Well, a recent measurement of the distance to Wolf 359 by a team of professional astronomers
yields a value of
Carnegie distance to Wolf 359 = 2.421 +/- 0.007 pc
Hmmm. My value does not agree (at the 1-sigma level) with the Carnegie value, even allowing for the stated uncertainties in each. Is there some reason that my value might be incorrect?
Yes, certainly. One implicit assumption that I made in my analysis was that all the stars (other than Wolf 359) in the images were at an infinite distance. I made this assumption by using the catalog positions for the stars as their "correct" positions as seen from Earth, and from New Horizons; only Wolf 359 was assumed to shift its apparent position due to parallax.
However, since none of the stars is really at an infinite distance, all of those reference stars should ALSO have shifted by some amount -- and in the same direction as Wolf 359. The Gaia satellite has measured the properties of billions of stars in our Milky Way Galaxy, including the stars I used as references in my analysis. You can see the parallax of those stars, in units of milli-arcseconds, on the graph below as a function of their apparent magnitude (bright stars at left, faint stars at right).
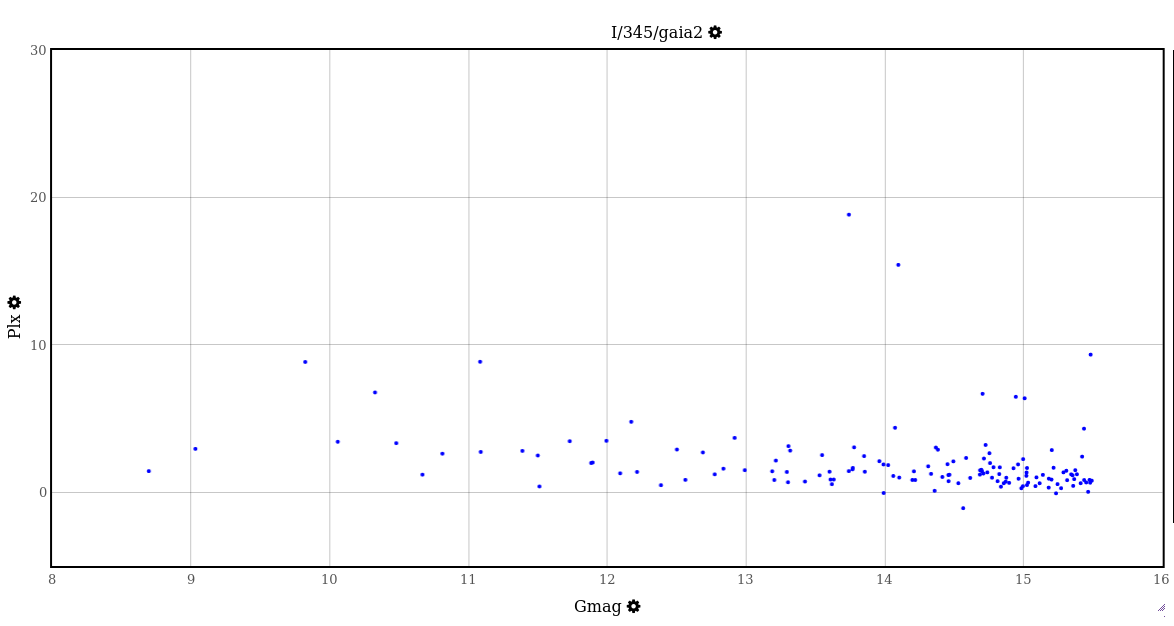
Two of these reference stars have parallax values greater than 10 milli-arcseconds, meaning that they are closer than 100 pc to the Earth.
In order to calculate the distance to Wolf 359 correctly, one would have to account for the shifts in all the reference stars. In other words, one would have to compute the apparent position of each star, from RIT and from New Horizons, and THEN determine the position of Wolf 359 based on those corrected positions. That's too much work for me.
But it is possible to figure out the DIRECTION of the error this would create in my results. Since all the reference stars would shift slightly in the same direction as Wolf 359, it means that the apparent shift in Wolf 359 we measured must be smaller than the true shift. Pretend for a moment that these other stars were at exactly the same distance as Wolf 359; then all the stars would shift by the same amount as Wolf 359, and in our comparison of the images, it would appear that Wolf 359 didn't move at all relative to the others.
So, our failure to account for the non-zero parallax shifts of the reference stars means that our measured shift in Wolf 359's position must be smaller than the true value; and that means that the distance we derived must be larger than the true distance. This is at least consistent with our result; I don't know if the effect explains the entire difference between our value and the true distance.
 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.