Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
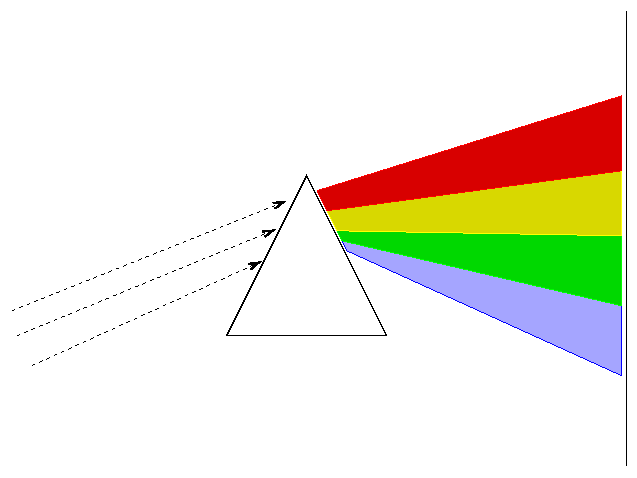
When astronomers send starlight through a prism or grating, they break the light into a spectrum:
If you examine the spectra of stars, you'll quickly discover that some are very different than others. For example, below are the spectra of three stars from a big survey: I've labelled them by their survey numbers.
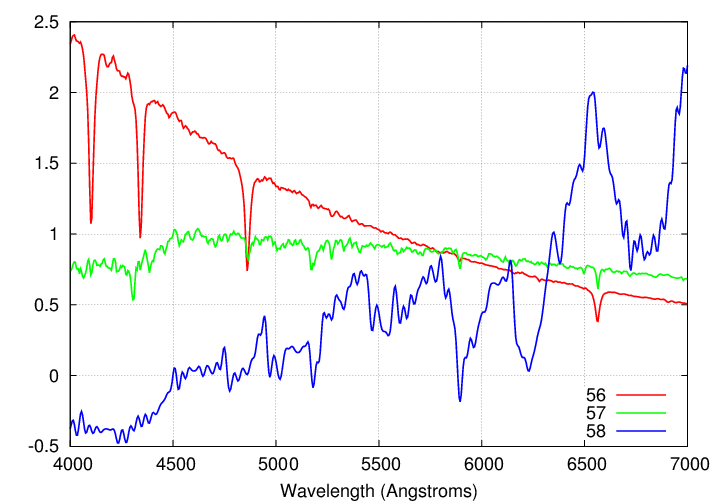
Q: Which star is the bluest? Q: Which star is the reddest?
Right. Stars which emit most of their light at short wavelengths appear blue, and those which emit most of their light a long wavelengths appear reddish.
Q: Why are some stars blue, and others red?
Right. The difference is temperature. Hot stars emit more blue light, while cool stars emit more red light. If you study physics, you'll find that there are mathematical relationships between the temperature of an object and the wavelength at which it emits most of its light.
Back in the early twentieth century, astronomers at the Harvard College Observatory figured all this out. They devised a system for classifying stars based on the properties of their spectra. They could easily distinguish the hot, blue stars from the cool, reddish ones.
Q: The Harvard astronomers assigned letters
to stars of different spectral types,
starting at the hot, blue end and going
to the cool, red end.
Can you name those letters?
hot cool
___ ___ ___ ___ ___ ___ ___
Very good!
hot cool
O B A F G K M
___ ___ ___ ___ ___ ___ ___
So, astronomers could use spectra to classify stars by their color or temperature. So far, so good.
Around 1912, two astronomers independently noticed something very interesting. They found that there was a relationship between the spectral class (or temperature) and absolute magnitude (or luminosity) for most stars .... not all stars, but most of them.
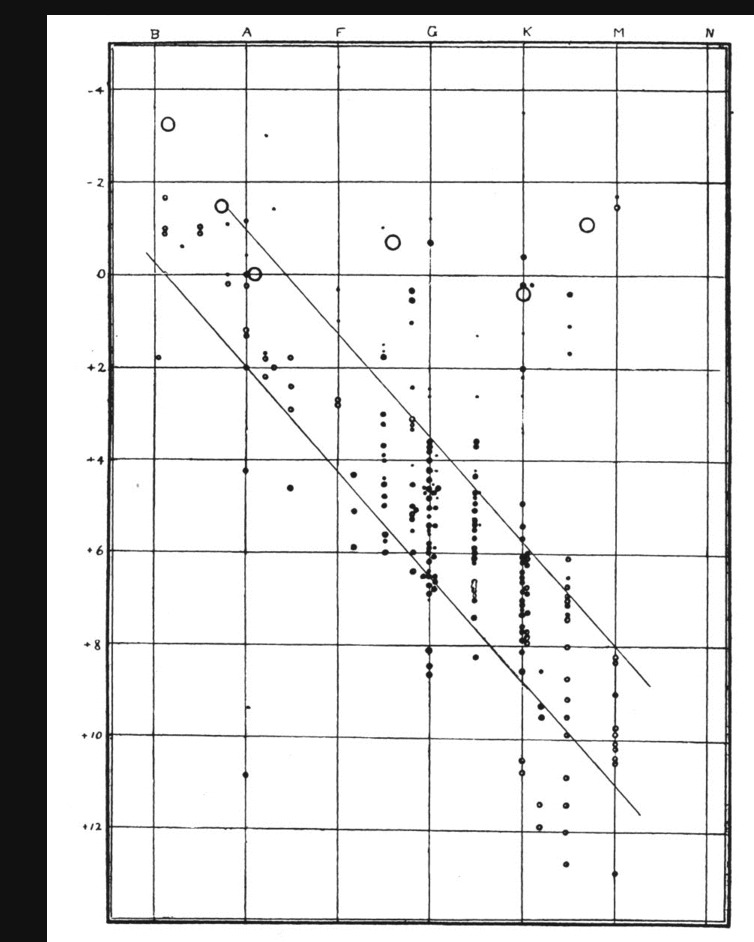
Q: Who were these astronomers?
Right. Ejnar Hertzsprung and Henry Norris Russell. We call the diagram they created the "Hertzsprung-Russell diagram", or "HR diagram" for short.
The HR diagram shows that most stars fall along a diagonal line, meaning that the hotter they are, the more light they emit. That makes sense. But not ALL stars fall on the diagonal line. Some cool, reddish stars, for example, lie far above it.
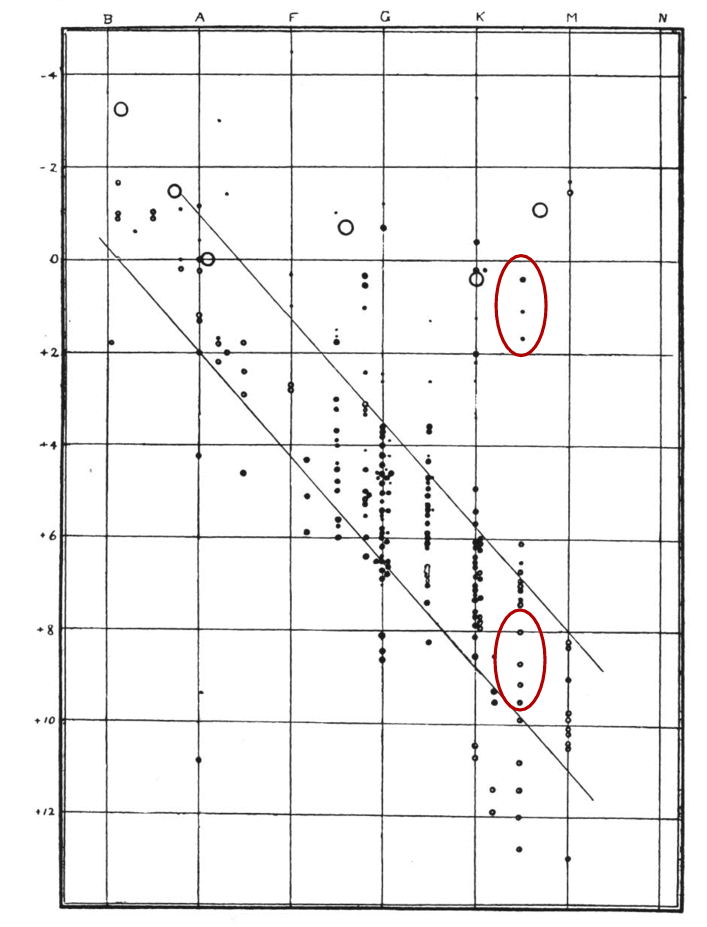
The stars in each region I've marked have the same temperature.
Q: How can some of these stars emit thousands
of times more light than the others?
Exactly. The stars in the upper-right hand region of the HR diagram must be much larger. We call them giants.
Now, this created a problem for astronomers. If two stars have the same color, and the same temperature, and the same spectrum, but very different sizes --- is there any way for us to tell them apart?
Alas, most stars are so far away from the Sun that even the most powerful telescopes can't resolve them; instead, the stars all appear as tiny little points of light. That doesn't help. Moreover, most stars are so far away that it's very difficult to measure their distances -- so, even if we could measure their apparent angular size (but we can't), we still would be unable to convert that angular size (arcseconds) to a linear size (meters).
Arrgggghhhh!!!!!
Fortunately, it turns out that there is a way to distinguish giant stars from dwarf stars, and it does involve spectra. But it requires a little something extra.
Here are three stars from the big survey. Each star has been classified as an "A0" star, so we think that the temperature of each one is identical. However, one of these stars is a giant.
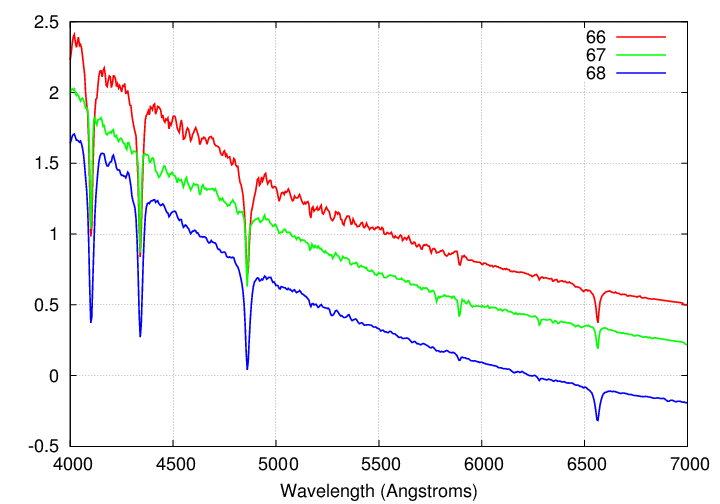
Q: Which star is the giant?
Not sure? Well, that's not surprising. I can't tell the difference between the stars, either. The problem is that the spectra you see above do not show sufficient detail. In order to discern fine details about a star, one needs to switch from low-resolution spectra to high-resolution spectra.
What does "resolution" mean in this context? It means "how finely is the light spread out into a spectrum?"
Let's look at a high-resolution comparison of these three stars:
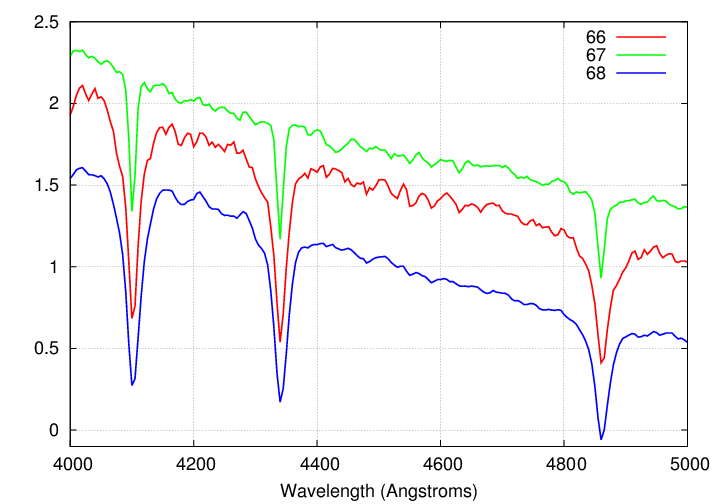
Now, let's pause for a moment to think about the physical nature of a star. A star contains a lot of mass, mostly in the form of hydrogen gas. The absorption lines we see in the spectrum of a star are formed in the outermost layers of its atmosphere, as light generated in the hot inner regions works its way out into space.
The absorption lines in our spectra are due to light which has been absorbed by atoms of hydrogen. Physicists have studied the absorption of light by hydrogen quite a bit. In theory, a single, isolated atom of hydrogen will always absorb light of very particular wavelengths. One of those wavelengths is 4861 Angstroms.
Again, in theory, a single, isolated atom will absorb light ONLY if the wavelength is exactly right: only 4861 Angstroms, not 4862 or 4860. And yet, when we look at real stellar spectra, we see that the absorption lines can be quite wide, spanning 3 or 5 or 10 Angstroms. What's going on?
One of the complications is that the atoms in a star are NOT isolated. They are surrounded by other atoms on all sides. Physicists have both theory and experimental evidence which indicates that, when an atom is surrounded by neighbors, its energy levels become slightly perturbed.
Image courtesy of HubPages
Ahem. So, if an atom is surrounded by other atoms, it will emit and absorb light at slightly different wavelengths. The more nearby neighbors at atom has, the more perturbed it will be, and the wider the range of wavelengths it might absorb.
Q: Which star has the LEAST perturbed hydrogen atoms? Q: Which star has the MOST perturbed hydrogen atoms?
Okay, we're almost there. You can tell from the high-resolution spectra that the atoms in star 67 have the fewest nearby neighbors.
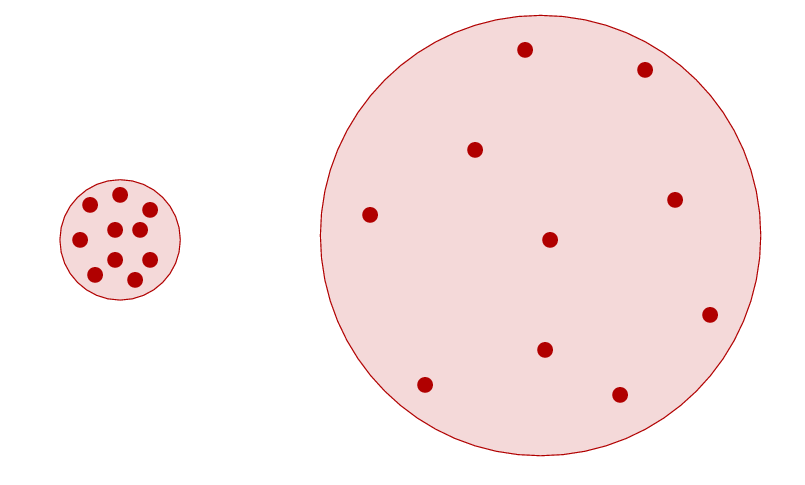
Q: In which of these stars will each atom
be more perturbed?
Indeed. If two stars have roughly the same mass, then atoms in the smaller one will be more densely packed and so have more nearby neighbors.
I think you are ready to answer the big question now.
Q: Which star is the giant (largest)? Q: Which star is the dwarf (smallest)?
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.