Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Contents
Astrometry is the measurement of the POSITIONS of objects in the sky; its partner is photometry, the measurement of BRIGHTNESS. There are two main facets of astrometry:
Each of these steps has its own methods and algorithms, with associated pitfalls and obstacles. As you might imagine, both involve a lot of MATH.
But today, I'd like to describe on particular application of astrometry: using small changes in the position of an object over the span of years to determine the distance to the object. This involves the concept of parallax.
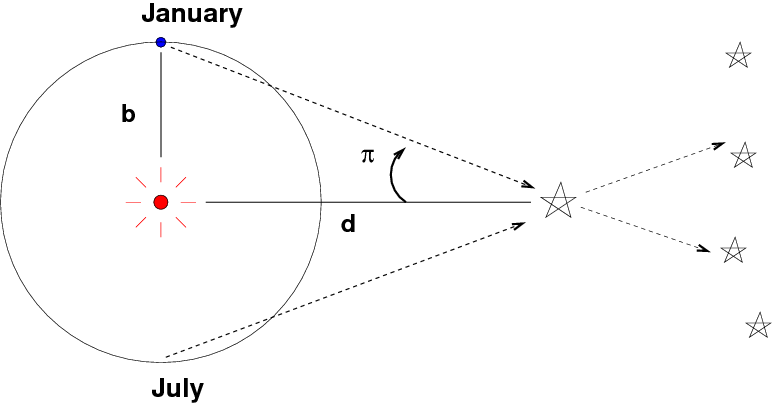
If one has measurements of the position of an object from two different locations, one can determine the distance to that object using a method called parallax. The basic idea is that the apparent location of a nearby object will appear to shift slightly, compared to the positions of distant objects, when seen from different locations. You've probably seen a diagram like the one below illustrating this principle in books and classes.
In 2002, the asteroid 2002 NY40 flew past the Earth at a distance of less than one million kilometers. I used a telescope at the RIT Observatory in upstate New York to take its picture ...
... at exactly the same time that one of my colleagues at the Naval Academy in Annapolis, MD, did the same with her telescope:
If you compare the two images carefully, you should see that the background stars line up in the two images -- but the nearby asteroid clearly "jumps" from one image to the next due to parallax. (Click on the image below to blink the images).
As the Earth orbits the Sun, our point of view shifts back and forth, and so we ought to see nearby stars also shift back and forth, back and forth, relative to the distant ones. Right?
Well, not quite. There's one additional complication, due to the motion of our solar system and other stars in the Milky Way Galaxy. Even though most stars are circling the center of the Galaxy in the same general direction, each moves with a slightly different speed and direction. The result is that, over periods of decades and centuries and millenia, nearby stars appear to drift slowly across the sky. We call this proper motion.
The stars in the Big Dipper, which are relatively close to the Sun (only about 20-30 parsecs away), provide a dramatic illustration. Click on the picture below to watch a movie showing 200,000 years of proper motion.
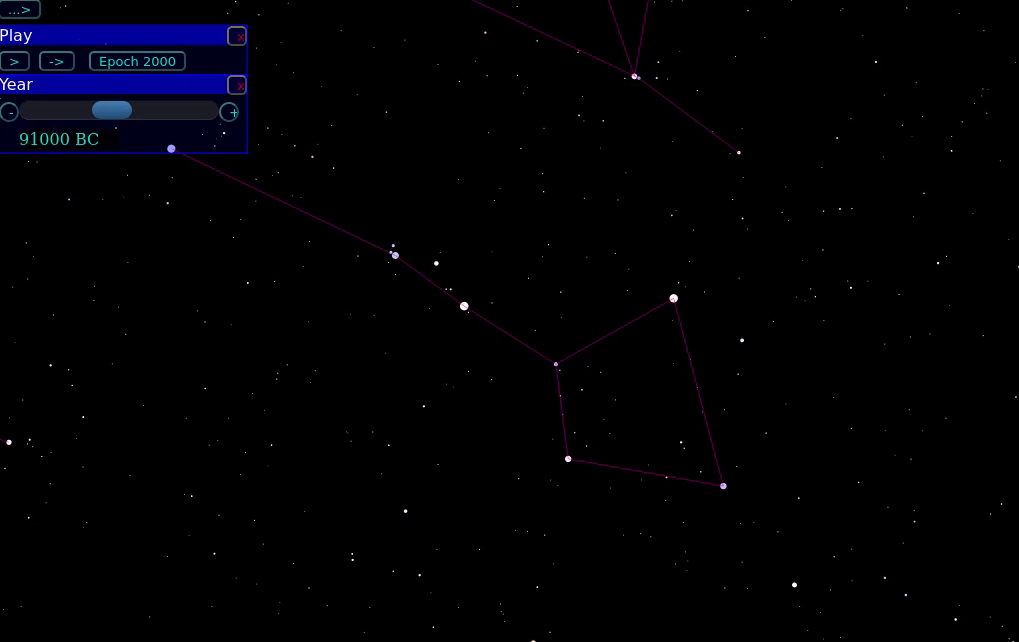
Movie courtesy of
Tony Dunn's proper motion simulator -- thanks, Tony!
So, if we make careful measurements of the position of a nearby stars over a period of several years, we expect to see it move in a path which combines
The result is something like a helix or corkscrew. You can see examples from the Hipparcos Intermediate Data archive by downloading and running their Java applet. The example below belongs to one of the brightest stars in the summer sky.
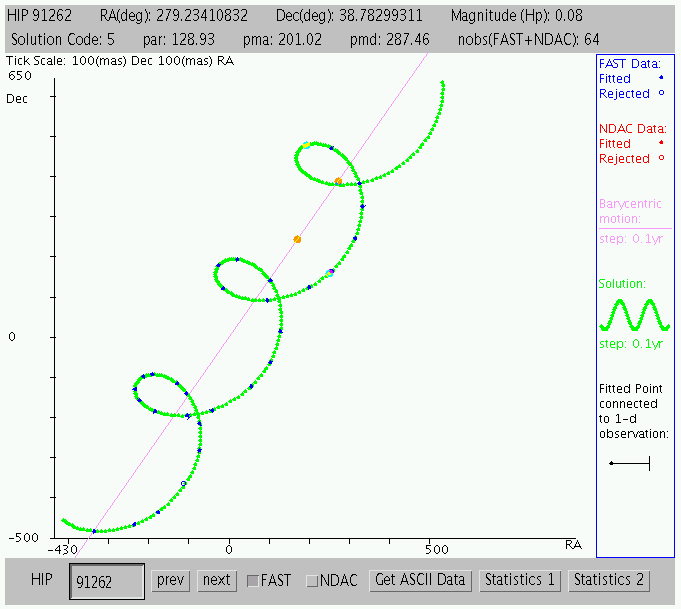
Thanks to the
European Space Agency
This seems relatively straightforward: take pictures of a nearby star 20 or 40 times over the course of several years, measure its position relative to distant stars carefully, fit a model consisting of some linear motion plus an elliptical component, and *poof* out pops the star's distance. What's so hard about that?
Well, I've neglected just one thing in this discussion so far: scale. Just how large are these motions? And how precisely can we measure the position of a star from a typical image?
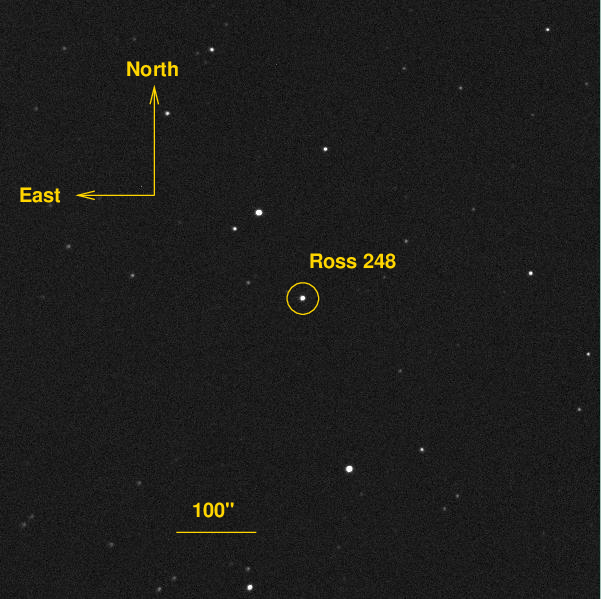
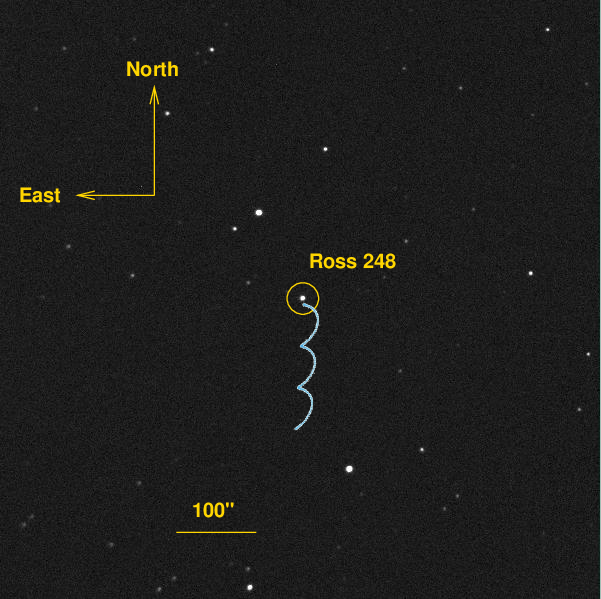
Consider the image below, which shows the nearby star Ross 248. This is one of many CCD images I have acquired of this star with the 12-inch telescope at the RIT Observatory.
The target has a proper motion to the South, so if we were to measure it over a three-year period, we ought to see it move in a pattern like this:
Simple, right? Measure the size of the "wiggles" in its motion, and use them to determine the parallax angle, and thence the distance to the star. Done!
There just one little complication. In the picture above, I've drawn the motion of Ross 248 in a slightly exaggerated way so that it's easier for you to see. The real motion is a bit smaller ...
The motion is somewhat smaller, so it's not quite so easy to measure accurately. Still, with some care, this is still not a big deal, right?
Nope, I'm lying. I still haven't drawn the motion at its proper size. Let's zoom in a bit more.
Okay, NOW I've drawn the motion of Ross 248 at its proper scale. Over this 3-year period, the star will move about 4.8 arcseconds to the South. Since the pixels on the camera at the RIT Observatory subtend 1.25 arcseconds each, this corresponds to a motion of about 3.8 pixels.
Oh, but wait -- it's not the long axis of this motion that we want to measure -- it's the short axis, running roughly East-West, representing the shift due to the Earth's motion around the Sun. What we really want to measure is THIS motion:
Of course, the full side-to-side motion is TWICE the parallax angle, so we really need to figure out half of that shift. As you can read elsewhere, in order to use parallax to determine the distance to a star accurately, one must measure the parallax angle with an uncertainty of at most ten percent. In the figure below, the red square illustrates the precision to which we must find that angle.
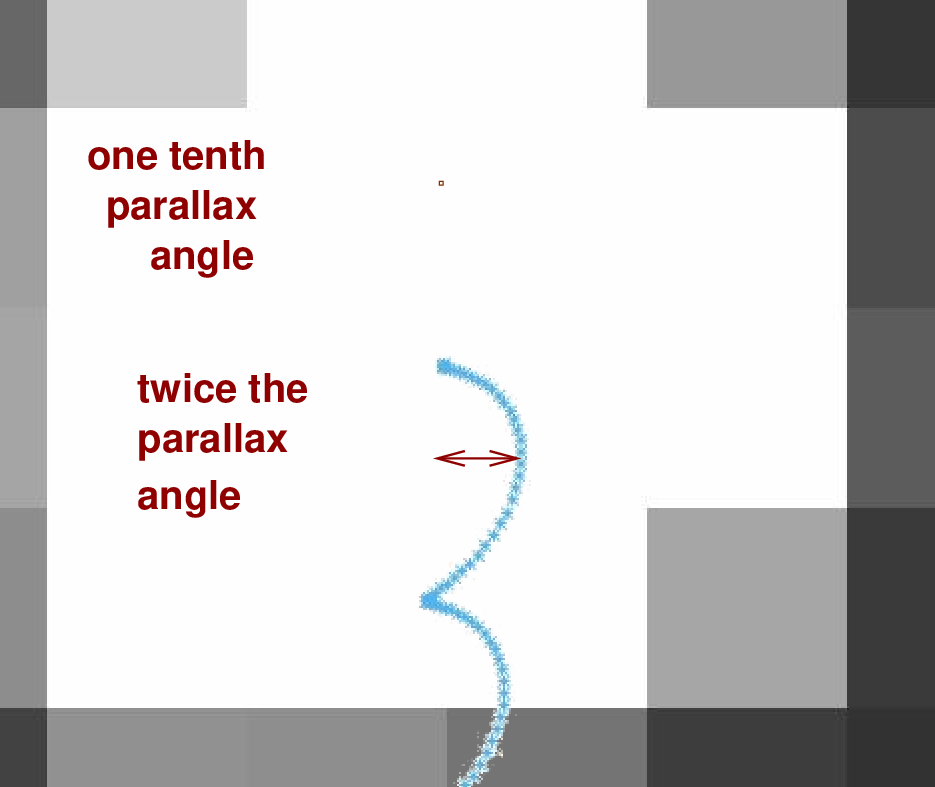
Oh, and one more thing: this particular example, Ross 248, is one of the closest stars to our solar system: the ninth-closest stellar system, in fact. A more typical parallax measurement requires precision which is 10 times, or even 100 times, higher than this.
NOW do you understand why astrometry is hard?
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.