 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Astronomers have their own ways of measuring objects in space. We've already encountered some of them --
but there are several more which appear frequently in discussions of stars (and other, more distant celestial objects). Let's start with the magnitude system, which astronomers use to describe brightness. Ordinary physicists often measure light in linear units, such as flux:
ergs Watt
flux of radiation = ---------- or --------
cm2 sec m2
This sort of linear quantity has a nice property: one can combine the light from several stars with simple addition.
Joe measures a flux from the star Vega of exactly 1,000,000 photons
per square cm per second.
Q: Suppose that two stars identical to Vega and at the same distance
were very close together in the sky, so that they appeared
as a single object in Joe's instrument.
What flux would Joe measure from this double-Vega system?
The answer is "2,000,000 photons/cm2 sec", of course. Linear fluxes are simple to use and make intuitive sense. More light means a bigger number. Simple. Easy.
However, astronomers (in the optical) don't often use this sort of unit to describe the brightness of stars. Instead, we use the magnitude system, which dates back (at least) to the catalog compiled by the Greek astronomer Hipparchus in the second century BC. The Greek astronomers recognized that some stars in the sky were brighter than others. They divided the stars into several groups, based on their visual appearance.

People today use a similar convention to rank a wide range of objects: surely you've heard phrases such as "a first-class hotel" or "a third-rate hamburger joint."
During the early 1800s, several scientists investigated the actual differences in brightness between stars which were one magnitude apart. They found a logarithmic relationship: adding one to the magnitude of a star corresponded to multiplying its flux by some factor, adding two to the magnitude of a star corresponded to multiplying its flux by (some factor)2, and so on. The ratio in brightness between two stars of magnitude N and (N + 1) was measured to have some value between 2 and 4, depending on the method used. In 1856, Henry Pogson realized that if one chose the factor of (100)1/5 = 2.512..., then a difference of 5 magnitudes would correspond to a ratio of intensity of exactly 100.
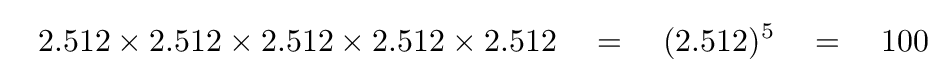
Astronomers eventually adopted this suggestion, though it took four or five decades to gain widespread acceptance. Mathematically, we can convert between intensity (a linear unit) and magnitude (a logarithmic quantity) in the following way. To turn intensities into magnitudes,
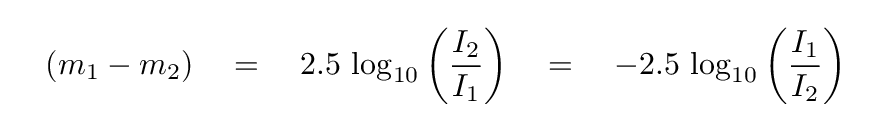
and to turn magnitudes into intensities,
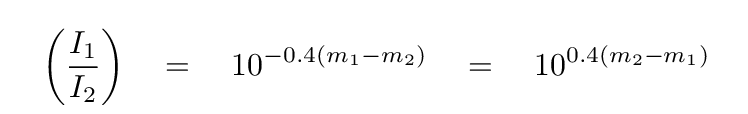
Note the negative signs in these expressions. Perhaps the most unfortunate feature of the magnitude scale is that it is backwards: large magnitudes correspond to faint sources.
Q: The star Vega has a magnitude of 0.0. If Vega is 10 times brighter
than Mintaka, what is the magnitude of Mintaka?
A second weakness of the magnitude system is that certain simple questions may not be so easy to answer.
Joe measures the magnitude of the star Vega to be exactly 0.00.
Q: Suppose that two stars identical to Vega and at the same distance
were very close together in the sky, so that they appeared
as a single object in Joe's instrument.
What magnitude would Joe measure from this double-Vega system?
Now, let's see what happens if we look at two stars of different temperatures through a set of filters: blue, green and red. The most common broad-band filters used by astronomers have names which almost make sense:
The most commonly used filters used to be B and V, though these days I is coming on strong. In many catalogs and databases, all you see is the B-band and V-band magnitudes for stars. SIMBAD, for example, by default shows a list like this:

When astronomers measure the magnitude of a star through one of these filters, they often use the name of the filter to describe their measurement:
V = 10.53 means "the apparent magnitude measured
through a V filter was 10.53"
Hot stars emit most of their light at short wavelengths: in the blue and ultraviolet. So when we measure their light through filters, we see
If we subtract the magnitude in the V filter from the magnitude in the V filter, we get a quantity, (B-V), which astronomers often call the "color" of the star. For a hot star, (B-V) is (small - large) = negative. So very hot stars have negative (B-V) colors.
On the other hand, cool stars emit most of their light in the red part of the spectrum.
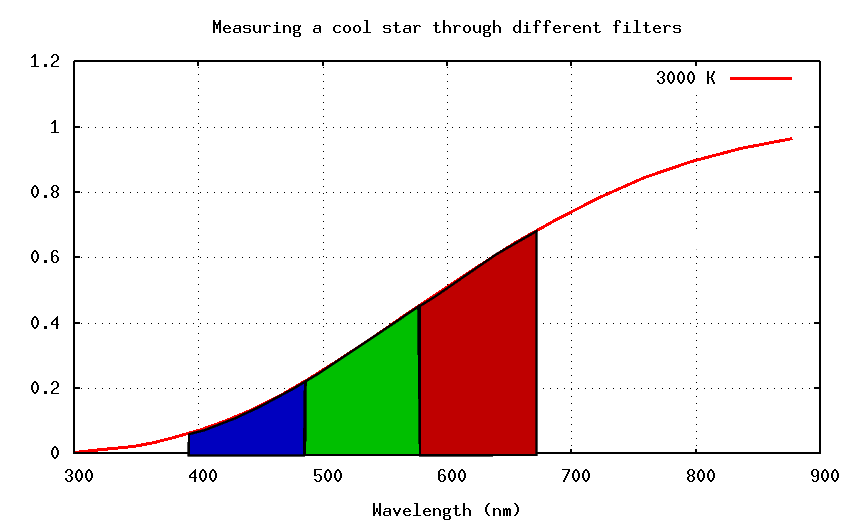
So when we measure their light through filters, we see
And the result is that (B-V) is (large - small) = positive. So cool stars have positive (B-V) colors. In short,
(B-V) color temperature
----------------------------------------------
small (< 0.5) hot
big (> 2.0) cool
----------------------------------------------
The color index of the Sun is about (B-V) = 0.6.
Sometimes, astronomers take a bit of a shortcut, and forget to say the word "index" in the phrase "color index." In the technical literature, it is common to see the "color" of a star described with a numerical value. One might read in a paper
HD 8396 has a (V-K) color of 1.93.
Ordinary stars emit the bulk of their luminosity via ordinary thermal processes, and so they exhibit roughly blackbody radiation. The details are rather complicated -- (if you are interested, you might look the notes from another course I have taught) -- but we'll ignore all those details. Astronomers have worked out a number of relationships between color index and the temperature of stars of various sorts. It's always a pretty rough connection, but can be very useful. For example, Sekiguchi and Fukugita, AJ 120, 1072 (2000) show
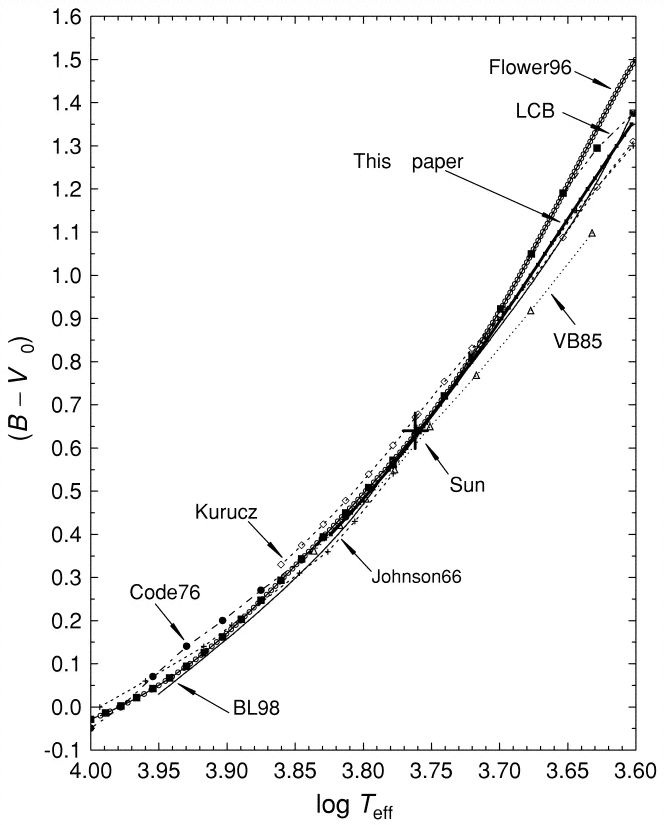
Q: What is the temperature of the Sun?
Q: What is the color index of a star with temperature 8000 K?
Q: What is the temperature of a star with a color index
(B-V) = 0.4?
The temperatures of ordinary stars span roughly one order of magnitude, ranging from very roughly 3,000 Kelvin to somewhere around 30,000 Kelvin. Our Sun is on the cool side.
Astronomers soon realized that there were two very different situations in which they wished to compare stars quantitatively:

Image courtesy of
Mighty Optical Illusions

Image from
The Usual Suspects
courtesy of
Park Circus .
We can observe the first, and then, if we know the distance to a star (which is not as easy thing to determine ...), we can compute the second. It turns out that there is a compact little mathematical relationship between these two quantities. Let's derive it.
Consider a star of luminosity L. If we place it at a distance d, then the intensity of its light will be
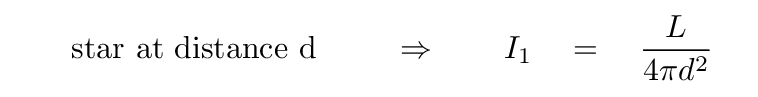
On the other hand, if we place it at some other distance D, then its intensity will have some different value:
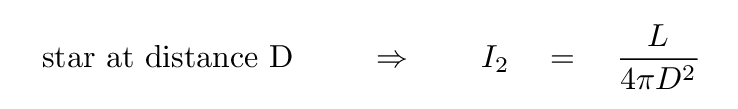
Now, the RATIO of these two intensities is easy to find; simply divide I1 by I2. Most of the terms will cancel, leaving only

But we're interested in magnitudes here. A ratio of intensities corresponds to a DIFFERENCE of magnitudes, due to the logarithmic nature of the magnitude system. So, let's compute the magnitude of each star and then subtract one from the other.
The magnitude of star at distance d can be written as
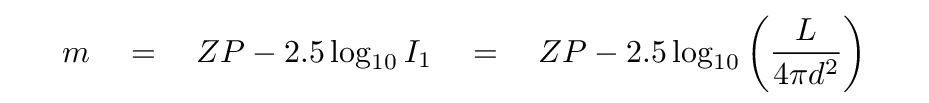
where ZP stands for the "zero point" of the magnitude scale in question. It will be some constant and arbitrary value, sometimes set by the magnitude of one particular star in the sky. Each photometric bandpass -- B, or V, or K -- has its own zero point.
Likewise, the magnitude of the same star at distance D must be
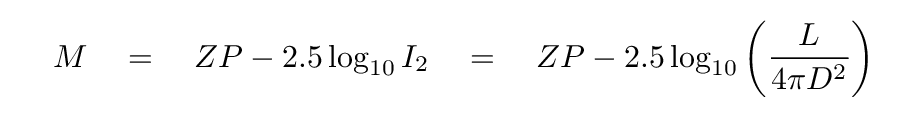
Q: What is the difference (m - M)? Please simplify it as far
as you can.
You should end up with
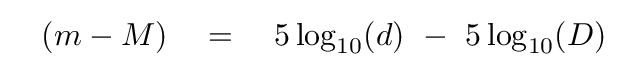
Now, suppose that we choose the distance D to be the "standard" distance for the police line-up of all the stars; in other words, let's make D be the distance we'll use to define absolute magnitudes. What distance would be a nice, convenient, round number?
How about D = 10 pc? If we chose that as our standard, then the formula for the difference between apparent and absolute magnitudes becomes very compact -- right?
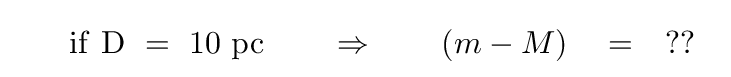
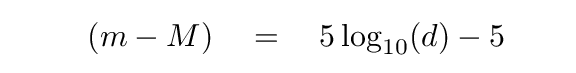
We call the quantity (m - M) the distance modulus. It's equivalent to some distance, of course, which we can calculatue using the above equation.
Q: The apparent magnitude of a star is m = 18, while its apparent
magnitude is M = 4. What is the distance to the star?
Since stars emit thermal radiation, we can use their spectra, or their colors, to estimate their temperatures. In a similar way, we can use the properties of blackbody radiation to determine the sizes of stars, at least to first order.
Consider a spherical star of radius R and temperature T which emits as a blackbody. Its luminosity must be
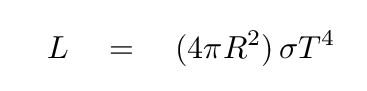
If the star lies a distance d from the Earth, then the flux of radiation we observe will be
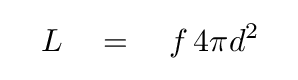
Q: Can you derive an equation for the radius R of the star
in terms of the observable quantities?
The answer is

Q: Suppose that our measurement of the distance d to a star
happens to be in error by 5 percent. What is the resulting
error in the radius of the star?
There are other ways that we can measure the sizes of some particular stars, often involving the occultation of a star by some second body (another star, or an asteroid, or the Moon).
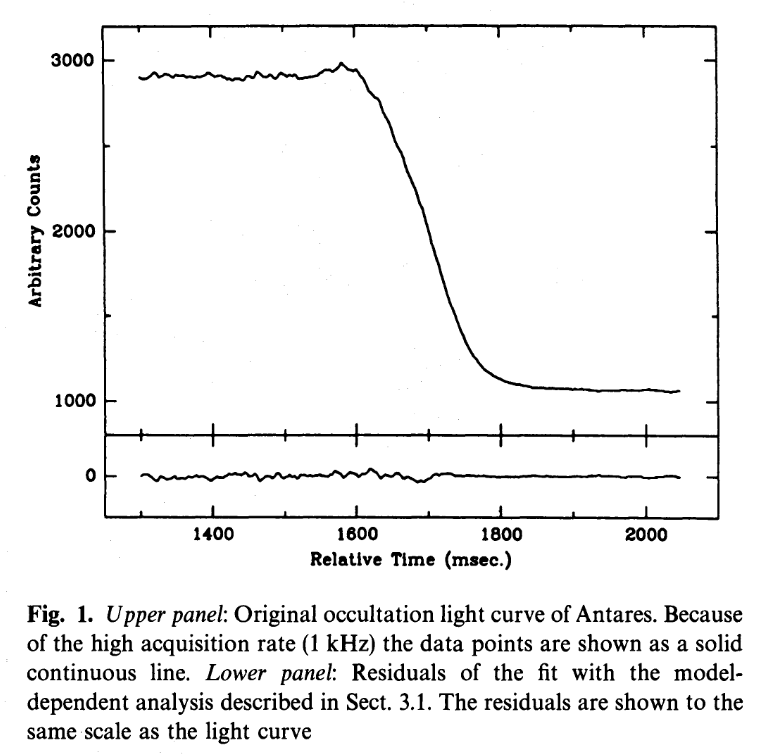
Figure 1 from
Richichi and Lisi, A&A 230, 355 (1990)
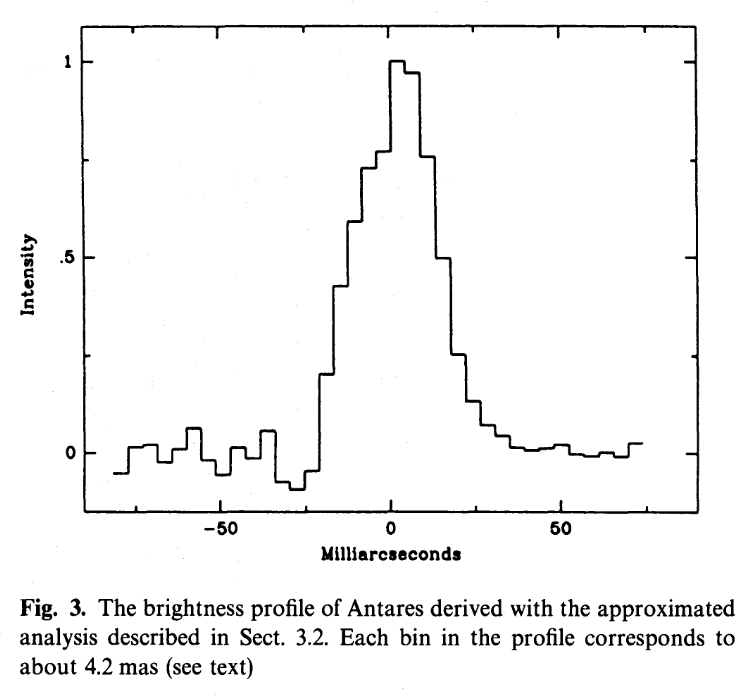
Figure 3 from
Richichi and Lisi, A&A 230, 355 (1990)
These independent measurements indicate that the simple method described above does a reasonable job in most cases. We can be confident, therefore, that we do know roughly how large stars can be.
The Sun -- with a radius of about R⊙ = 7 x 108 m -- lies in the middle of a large range. The biggest ordinary stars are about ten times larger, while the smallest ordinary stars are about ten times smaller.

Image courtesy of
ESO/M. Kornmesser
There are a number of ways that astronomers can determine the mass of a star, but one of the primary methods involves good old physics. You may recall that a certain Johannes Kepler found a relationship between the period of an orbit, P, and the semimajor axis of that orbit, a.
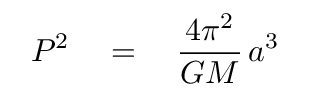
Now, suppose two stars orbit around each other in a binary system. If the system is close enough to the Sun, then we might be able to resolve each star, and watch them as they move around each other. The bright star Sirius is an example of such a "visual binary system".
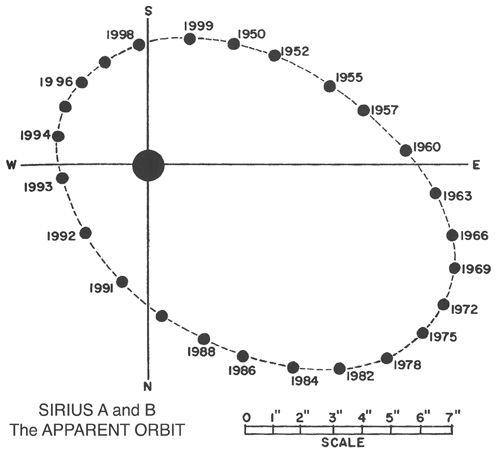
Image courtesy of
Burnham's Celestial Handbook
Notice that what we can measure with our telescopes is the ANGULAR motion of one star around the other -- in other words, a measurement of distance between the two in degrees, or arcseconds, or radians. Kepler's Law, in its variable a, calls for a LINEAR separation between the stars -- in units of meters, or Astronomical Units.
Q: How can we convert an ANGULAR separation into a LINEAR separation?
Exactly. We need to multiply the ANGULAR separation by the DISTANCE to the star. And, since we can measure the distances to nearby star systems, we can use this technique to determine the masses to some nearby binary stars.
It turns out that, once again, our Sun is just an ordinary star, lying in the middle of the pack: it has a mass of about M☉ = 1.99 x 1030 kg. The most massive stars are 50-100 times more massive than the Sun, while the least massive are about 1/10 the Sun's mass.
Now -- what if our distance measurements aren't quite correct? Any error we make in measuring the distance to the star will be propagated into an error in the linear separation a. For example, if our value for the distance is 10% too large, then the value for the linear separation a will also be 10% too large. That seems simple enough.
However, look at the result on a subsequent calculation of the MASS of the stars. Let's re-arrange Kepler's Third Law so that we solve for the mass in terms of everything else.
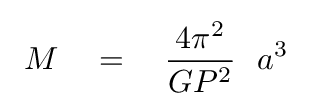
The mass is proportional to the linear separation to the third power --- and there's the issue: any mistake in the measurement of distance to the binary system will be amplified when we apply that distance in our calculation of the mass. In fact, a 10% error in distance will turn into a 30% error in stellar mass!
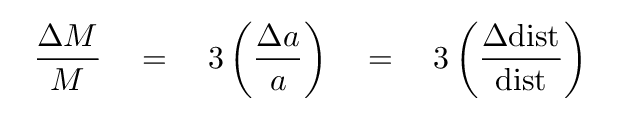
The bottom line is -- even small mistakes in distance measurements can have big consequences in our understanding of stellar masses.
 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.