 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Astronomy is one of the oldest sciences, if not THE oldest. Its history is part of its charm (to me, at least), but is also responsible for some unfortunate consequences. Most of the major observational tasks for ancient astronomers were very large affairs, taking years or decades of effort. As a result, when the information collected by older generations was passed on to younger scientists, it was usually cherished and preserved, rather than being tossed aside and replaced. Astronomy has therefore inherited a number of terms and units from its past, which are still used today in the technical literature. In order to understand modern astronomy, one must understand these relics of the past.
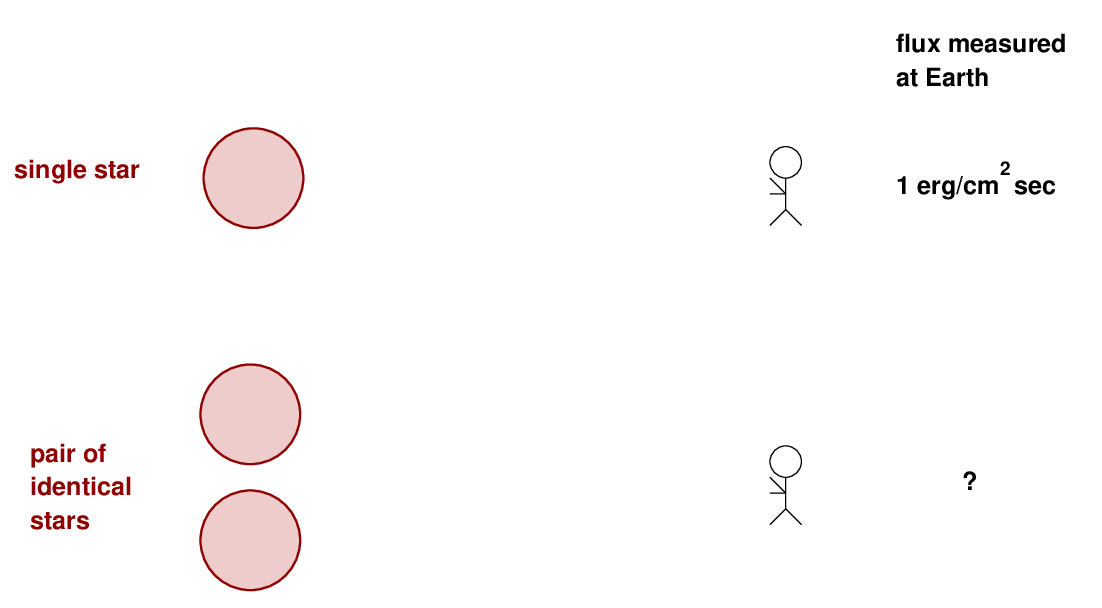
Clearly, astronomers need some way to describe the brightness of stars. If we were to start from scratch -- as radio astronomers did when they turned their equipment to the skies after World War II -- we would probably choose some unit like their Jansky: one which measures the intensity or flux of light in linear terms. For example, we might choose to measure the amount of radiation passing through a given area in one second:
ergs Watt
flux of radiation = ---------- or --------
cm^2 sec m^2
This sort of linear quantity has a nice property: one can combine the light from several stars with simple addition.

Q: What is the brightness of the double-star system, expressed
in linear flux units?
The answer is "2 ergs/cm2 sec", of course. Linear fluxes are simple to use and make intuitive sense. More light means a bigger number. Simple. Easy.
However, astronomers (in the optical) don't often use this sort of unit to describe the brightness of stars. Instead, we use the magnitude system, which dates back (at least) to the catalog compiled by the Greek astronomer Hipparchus in the second century BC. The Greek astronomers recognized that some stars in the sky were brighter than others. They divided the stars into several groups, based on their visual appearance.
People today use a similar convention to rank a wide range of objects: surely you've heard phrases such as "a first-class hotel" or "a third-rate hamburger joint."
Although Hipparchus' catalog has been lost, much of his work was copied into the catalog of Ptolemy in the second century AD, and that has been preserved.
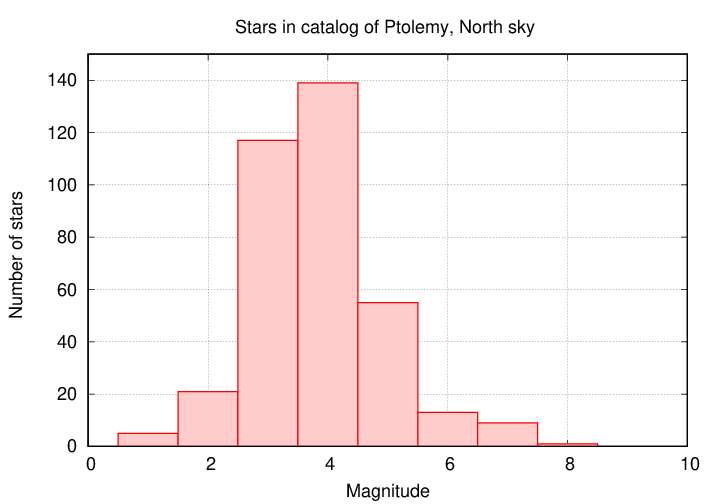
In the eighteenth and nineteenth centuries, advances in technology allowed astronomers to build better telescopes, so that they could see much fainter stars ... and to build devices which allowed them to make QUANTITATIVE measurements of stellar brightness. They found, for example, that the flux of a bright star of magnitude 1 was roughly 100 times larger than the flux from a faint star of magnitude 6. The question became -- "is there any way to retain most of the traditional measurements, yet put them on a modern, quantitative, system?"
During the early 1800s, several scientists investigated the actual differences in brightness between stars which were one magnitude apart. They found a logarithmic relationship: adding one to the magnitude of a star corresponded to multiplying its flux by some factor, adding two to the magnitude of a star corresponded to multiplying its flux by (some factor)2, and so on. This wasn't surprising: several human senses work in this manner. Human hearing, for example, considers three sounds to increase in volume by equal amounts ("loud", "loud + 1 step", "loud + 2 steps") when the intensity of the sound waves increases by equal factors ("1 x 10-6 W/m^2", "3 x 10-6 W/m^2", "9 x 10-6 W/m^2").
The ratio in brightness between two stars of magnitude N and (N + 1) was measured to have some value between 2 and 4, depending on the method used. In 1856, Henry Pogson realized that if one chose the factor of (100)1/5 = 2.512..., then a difference of 5 magnitudes would correspond to a ratio of intensity of exactly 100.
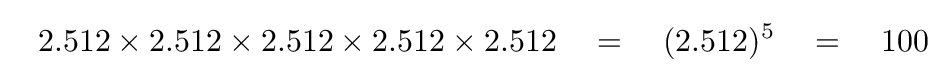
Astronomers eventually adopted this suggestion, though it took four or five decades to gain widespread acceptance. Mathematically, we can convert between intensity (a linear unit) and magnitude (a logarithmic quantity) in the following way. To turn intensities into magnitudes,
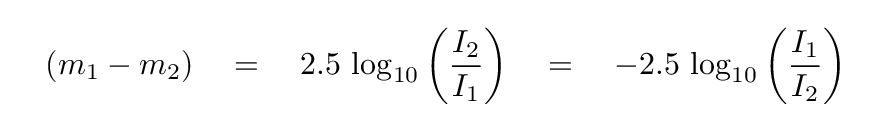
and to turn magnitudes into intensities,
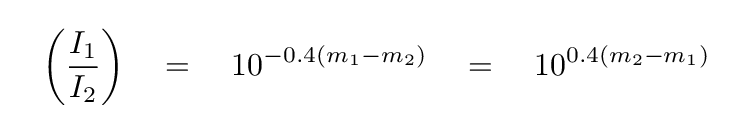
Note the negative signs in these expressions. Perhaps the most unfortunate feature of the magnitude scale is that it is backwards: large magnitudes correspond to faint sources.
Q: If Vega is 10 times brighter than Mintaka, what is the
magnitude of Mintaka?
A second weakness of the magnitude system is that certain simple questions may not be so easy to answer.
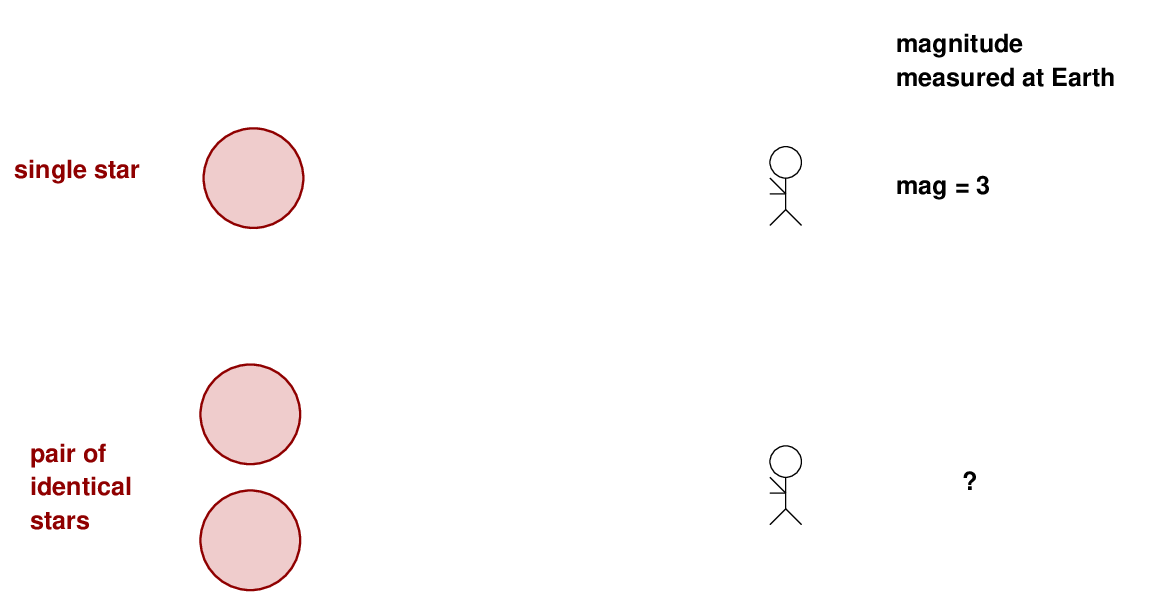
Q: What is the brightness of the double-star system, expressed
in magnitudes?
Now, let's see what happens if we look at two stars of different temperatures through a set of filters: blue, green and red. The most common broad-band filters used by astronomers have names which almost make sense:
The most commonly used filters used to be B and V, though these days I is coming on strong. In many catalogs and databases, all you see is the B-band and V-band magnitudes for stars. SIMBAD, for example, by default shows a list like this:

When astronomers measure the magnitude of a star through one of these filters, they often use the name of the filter to describe their measurement:
V = 10.53 means "the apparent magnitude measured
through a V filter was 10.53"
Hot stars emit most of their light at short wavelengths: in the blue and ultraviolet. So when we measure their light through filters, we see
If we subtract the magnitude in the V filter from the magnitude in the V filter, we get a quantity, (B-V), which astronomers often call the "color" of the star. For a hot star, (B-V) is (small - large) = negative. So very hot stars have negative (B-V) colors.
On the other hand, cool stars emit most of their light in the red part of the spectrum.
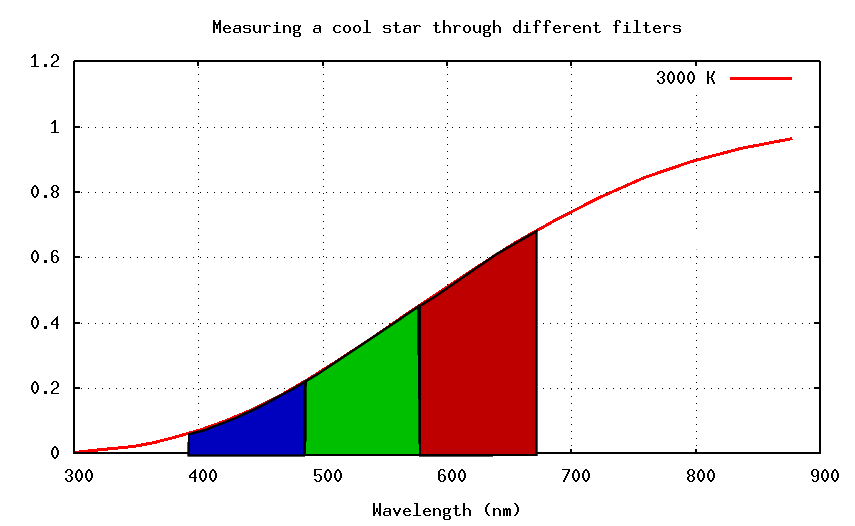
So when we measure their light through filters, we see
And the result is that (B-V) is (large - small) = positive. So cool stars have positive (B-V) colors. In short,
(B-V) color temperature
---------------- ------------
small (< 0.5) hot
big (> 2.0) cool
The color index of the Sun is about (B-V) = 0.6.
Sometimes, astronomers take a bit of a shortcut, and forget to say the word "index" in the phrase "color index." In the technical literature, it is common to see the "color" of a star described with a numerical value. One might read in a paper
HD 8396 has a (V-K) color of 1.93.
Astronomers have worked out a number of relationships between color index and the temperature of stars of various sorts. It's always a pretty rough connection, but can be very useful. For example, Sekiguchi and Fukugita, AJ 120, 1072 (2000) show
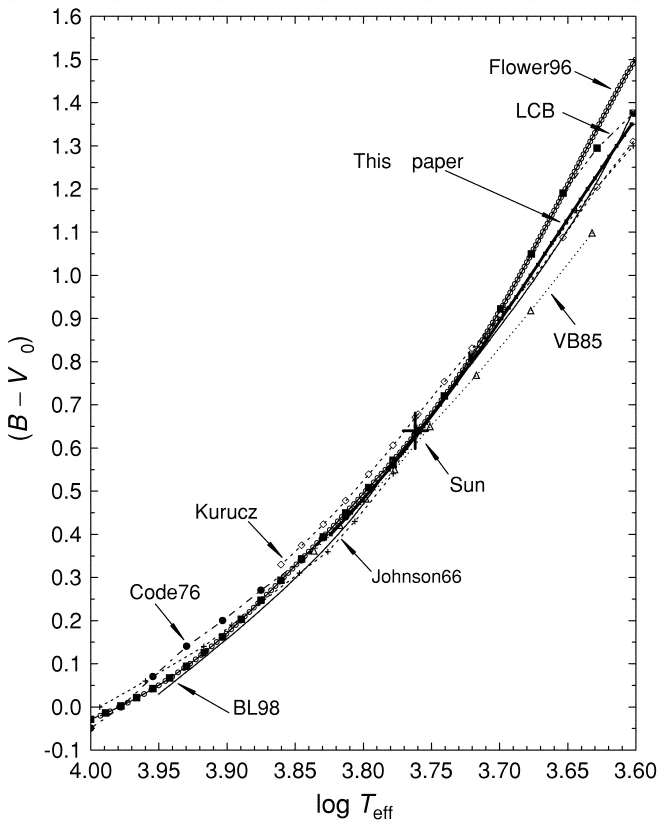
Q: What is the temperature of the Sun?
Q: What is the color index of a star with temperature 8000 K?
Q: What is the temperature of a star with a color index
(B-V) = 1.0?
Astronomers soon realized that there were two very different situations in which they wished to compare stars quantitatively:

Image from
The Usual Suspects
courtesy of
Park Circus .
We can observe the first, and then, if we know the distance to a star (which is not as easy thing to determine ...), we can compute the second. It turns out that there is a compact little mathematical relationship between these two quantities. Let's derive it.
Consider a star of luminosity L. If we place it at a distance d, then the intensity of its light will be
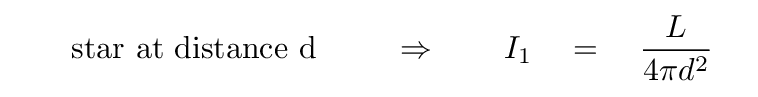
On the other hand, if we place it at some other distance D, then its intensity will have some different value:
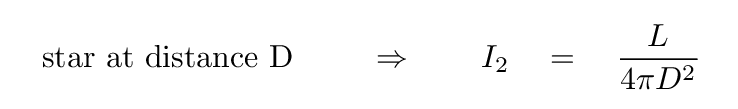
Now, the RATIO of these two intensities is easy to find; simply divide I1 by I2. Most of the terms will cancel, leaving only
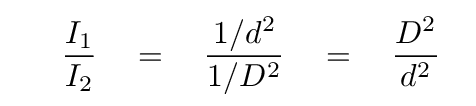
But we're interested in magnitudes here. A ratio of intensities corresponds to a DIFFERENCE of magnitudes, due to the logarithmic nature of the magnitude system. So, let's compute the magnitude of each star and then subtract one from the other.
The magnitude of star at distance d can be written as
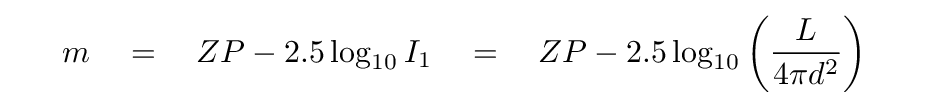
where ZP stands for the "zero point" of the magnitude scale in question. It will be some constant and arbitrary value, sometimes set by the magnitude of one particular star in the sky. Each photometric bandpass -- B, or V, or K -- has its own zero point.
Likewise, the magnitude of the same star at distance D must be
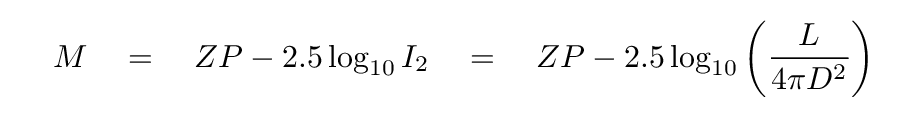
Q: What is the difference (m - M)? Please simplify it as far
as you can.
You should end up with
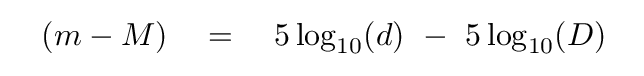
Now, suppose that we choose the distance D to be the "standard" distance for the police line-up of all the stars; in other words, let's make D be the distance we'll use to define absolute magnitudes. What distance would be a nice, convenient, round number?
How about D = 10 pc? If we chose that as our standard, then the formula for the difference between apparent and absolute magnitudes becomes very compact -- right?
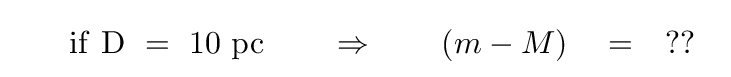
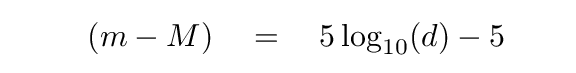
In the ordinary world, we often measure the sizes of objects, and the distances between them, using the fundamental unit of the meter, together with a parade of prefixes.
This is a handy system: by picking the proper prefix, we can usually describe some particular object with a numerical value between 1 and 1000, which is easy to say and to compare with other values. Moreover, it only takes five or six prefixes to cover (almost) the entire range of objects studied in many fields of science. Performing calculations is a piece of cake, since all the conversions are just factors of ten.
But ... as a wise man once said,
Space is big. Really big. You just won't believe how vastly, hugely, mind-bogglingly big it is. I mean, you may think it's a long way down the road to the chemist, but that's just peanuts to space.
Douglas Adams, "Hitchhiker's Guide to the Galaxy"
Space is so-o-o-o big that it breaks the usual metric system. In order to describe the distances between planets in the solar system, one can get away with giga-meters, or maybe tera-meters; but the distances between stars, or galaxies, require prefixes so infrequently used elsewhere that few can remember them.
Therefore, astronomers have decided to create their own units, which are just the right size to make some frequently discussed quantities fit into the comfortable range of 1 to 1000.
The three most common of these "special" astronomical quantities are
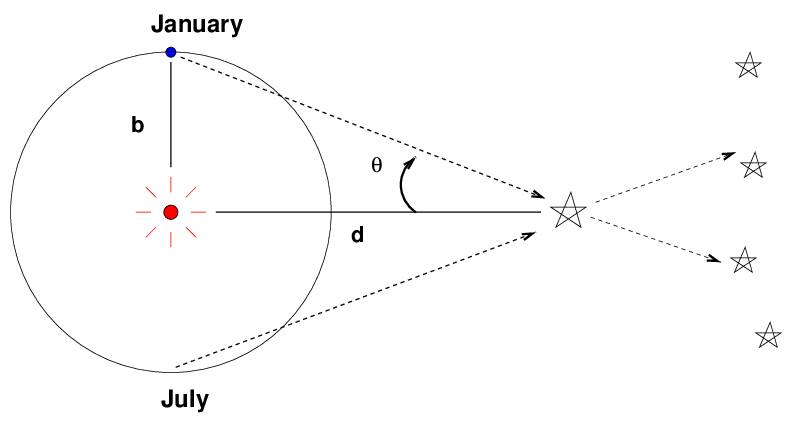
The parsec is a good unit for measuring distances between stars, as the typical distance between stars in our neighborhood of the Milky Way is just about 1 pc.
 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.