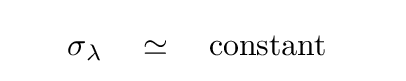
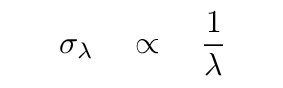
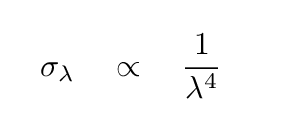
 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
The goal of today's lecture is to investigate the conditions under which a cloud of gas and dust in the interstellar medium might collapse under the force of gravity. This is a VERY complicated topic, and the astronomical community is in the early stages of understanding star formation. We will focus on one aspect of the issue, and (as usual) make several simplifying assumptions. The main result is built on the work of English astronomer James Jeans.
The InterStellar Medium (ISM) is a complex mixture of materials: tendrils of hot, tenuous gas at temperatures of millions of degrees, threading through large regions of gas and dust at moderate temperatures, and studded here and there with dense clouds inside which the temperature drops to 100 K or even lower. It doesn't make much sense to discuss an "average" density or temperature. Instead, it's best to focus on one component of the ISM at a time.
Today, we'll stick with the cold, dense clouds. Inside the clouds, atoms and molecules stick together to form dust particles, which are very effective at blocking and scattering light. We can use the ideas we learned earlier, such as mean free path and optical depth, to estimate roughly the effect of a dense cloud on starlight which passes through it.
Consider a cloud which is D = 1 pc thick. Inside the cloud are tiny dust particles with a density of n = 10-3 particles/cubic meter. To a _very_ rough approximation, we can treat the particles as perfectly opaque spheres of radius r = 2 x 10-7 m.
Q: What is the mean free path of light inside this cloud?
Q: What is the optical depth of the cloud?
Q: How many magnitudes of extinction will a star suffer
as its light must pass through this cloud?
Now, in the example above, we've assumed that light of all wavelengths will be scattered or absorbed equally well by the dust particles. In real life, that's not true. The details are rather complicated, but there are several regimes in which the relationship between wavelength and effective cross section are simple.
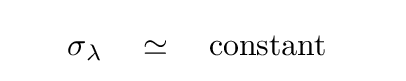
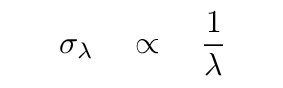
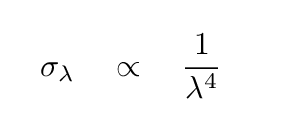
The last situation is known as the Rayleigh regime, and the results should be very familiar to you from your everyday experiences on planet Earth.
Now, these rules are just rough guides to the real interaction of matter and light. Things always grow more complicated when one examines the real world closely. For example, in the optical range, the wavelength of light is roughly the same as the size of dust particles. We would therefore expect that the extinction should grow linearly as we move from the red end of the optical to the blue end, and on into the ultraviolet. The graph below shows measurements of extinction as a function of (1 / λ), and the general trend IS roughly linear, as expected.
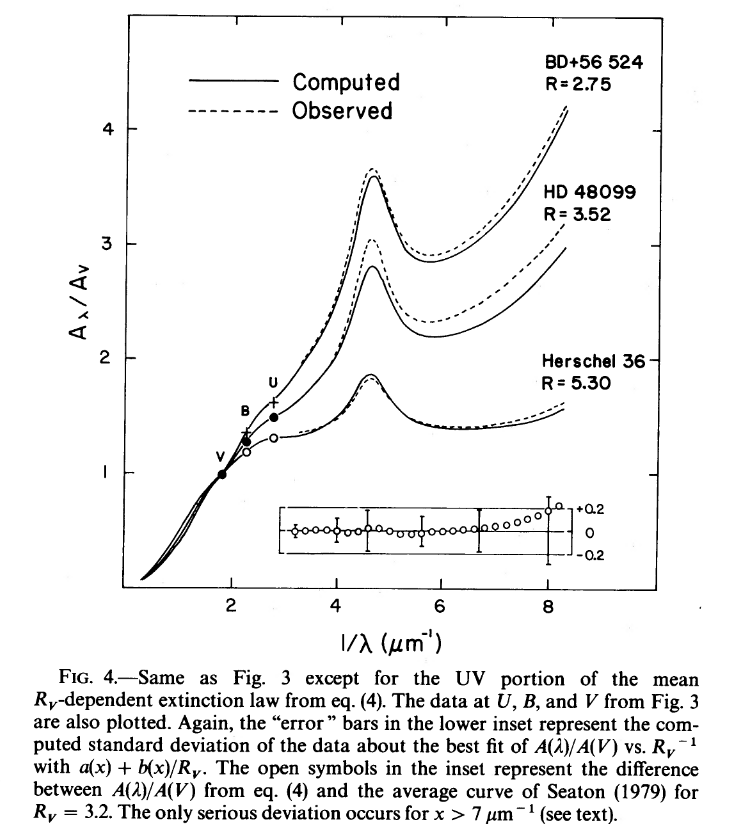
Figure 4 taken from
Cardelli, Clayton and Mathis, ApJ 345, 245 (1989)
But look at the feature, sometimes called the "big blue bump", at a wavelength of about 2175 Angstroms = 0.2175 microns. This may be due to graphite molecules with the dust particles. Other features appear in the infrared. Extinction by dust and gas in the ISM is not a simple matter!
But the main topic of today's lecture is not the behavior light passing through a cloud, but the behavior of the cloud itself over time. Let's look at the battle between gravity and thermal motions for the fate of an interstellar cloud.
There is a particularly simple -- and useful! -- relationship between bodies in an isolated, self-gravitating system. If one computes both the total kinetic energy of the objects, K, and the total gravitational potential energy of the objects, U, then if the system is in stable equilibrium
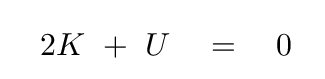
This is known as the virial theorem.
Note that the sum is zero only if the system is in a stable equilibrium; for example, the planets orbiting the Sun in our Solar System. If the system is not in equilibrium, then the sum will not be zero.
Let's do two quick examples to see how this works.
Q: What will happen to these two atoms?
Q: What will happen to these two objects?
Consider a cloud of gas floating in interstellar space. Each atom or molecule in the cloud has some kinetic energy, but all the particles are drawn to each other via their mutual gravitational forces. What will happen to the cloud over some long period of time?
With a few simplifying assumptions, we can determine the fate of this cloud using the virial theorem. First, we'll assume that there are no bulk motions of gas in the cloud, so that all the kinetic energy is due to the random thermal motions of the particles. In that case,
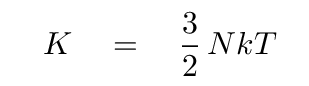
The number of particles, N, is a rather awkward parameter. It would be better if we could express this kinetic energy in terms of more easily observable quantities, such as the radius and density of the cloud.
Q: Assume that the density of the cloud is constant, and that
its mean molecular weight is μ.
Can you write an expression for the kinetic energy of the cloud
in terms of its radius R and density ρ?
Right.
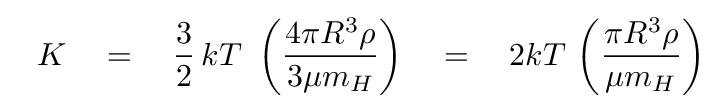
Okay, so much for the kinetic energy (KE). We now need an expression for the gravitational potential energy (GPE) of a cloud of gas of uniform density. Hmmm. Well, as we have seen earlier, the GPE of a uniform sphere of mass M and radius R can be written as
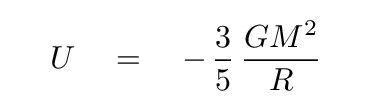
Q: Assume that the density of the cloud is constant, and that
its mean molecular weight is μ.
Can you write an expression for the GPE of the cloud
in terms of its radius R and density ρ?
Right again.
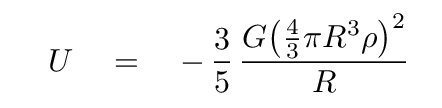
Hmmm. That's a bit messy. Let's simplify it.

That's better.
Okay, we can now apply the virial theorem to this question of the fate of a cloud. The cloud will remain be (and remain) in static equilibrium if twice the kinetic energy equals the absolute value of the gravitational potential energy. So, if we insert our expressions for the KE and GPE into this equality, we find equilibrium will occur if
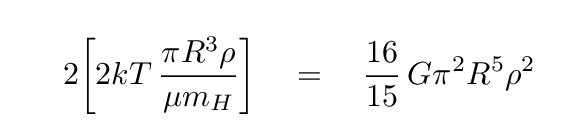
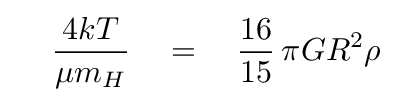
Q: Can you solve for the critical radius R, sometimes called the Jeans' length,
at which a cloud will be at equilibrium?
Q: If the cloud is larger than this critical value, will it expand or collapse?
The critical size of the cloud (aka Jeans' length) is
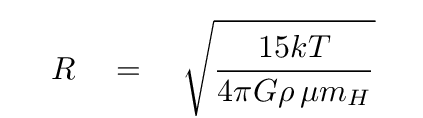
If a cloud is larger than this threshold, which way will it evolve? Look at one of the early expressions for equilibrium: kinetic energy on the left, (absolute value of) gravitational potential energy on the right.
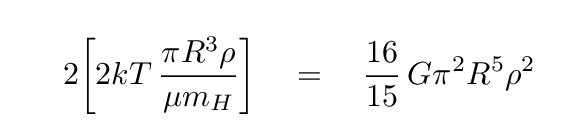
The KE grows with radius to the third power, but the magnitude of the GPE grows with radius to the FIFTH power; so, if the cloud exceeds the Jeans' length, the GPE will overwhelm the KE, and the cloud will collapse.
There's another way to test the fate of a cloud based on the virial theorem; but instead of focusing the size of the cloud, this approach uses its MASS as the disciminating quantity. Look at the expression for the kinetic energy of all the particles in a cloud:
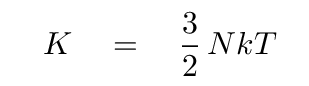
The number of particles, N, can be expressed as the mass of the entire cloud, divided by the average mass of a particle: N = M / (μ mH). If we make this substitution, then the condition for static equilibrium becomes

Q: Can you re-arrange this equation to solve for the mass?
Yup, not too hard.
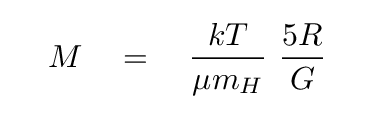
This equation has a factor of R, but we can express the radius in terms of the mass and average density.

If one makes this substitution, and then performs several lines of algebra, one can finally write the condition for static equilibrium in terms of mass, temperature, density, and mean molecular weight. This is the Jeans' mass.
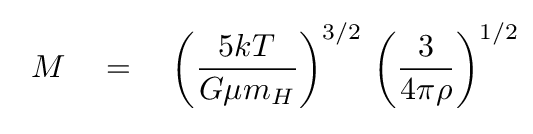
Q: If a cloud is more massive than this critical value, will it expand or collapse?
Over the past few decades, astronomers have pointed radio, infrared, and sub-millimeter telescopes at giant molecular clouds in order to pierce through the veil of dust and measure the properties of dense knots and clumps. The differences between the view in the optical and the much longer wavelengths can be profound.
For example, consider the region known as S237 or NGC 1931. In red optical light, there's a bit of nebulosity.

But images taken by the Herschel space telescope at far-IR wavlengths show a much larger expanse of cool gas and dust.

Image taken from Figure 1 of
Dewangan et al., ApJ 834, 22 (2017)
In the paper Probing fragmentation and velocity sub-structure in the massive NGC 6334 filament with ALMA , Shimajiri et al. measure the properties of clumps of gas deep within a molecular cloud known as NGC 6334, using the Atacama Large Millimeter Array (ALMA). In one region of this complex, they see a series of dense clumps along a filament of gas:

Image taken from Figure 1 of
Shimajiri et al., A&A 632, 83 (2019) ,
based on data described in
Andre et al., A&A 592, 54 (2016)
The authors list the properties of these clumps in their Table 4:

Table 4 taken from
Shimajiri et al., A&A 632, 83 (2019) ,
We can take typical values of the gas in these clumps as
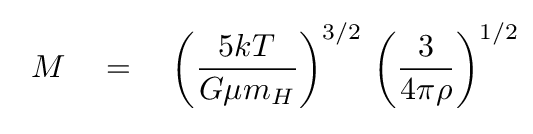
Q: Can you compute the Jeans mass for gas with these properties?
Q: Look in the table for the actual mass estimates for these clumps.
What is their fate?
We can also compare the sizes of these clumps to the Jeans' length. Remember that the Jeans' length can be written
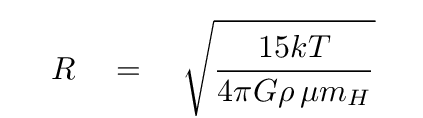
Q: Can you compute the Jeans length for gas with these properties?
Q: Look in the table for the actual measured sizes of these clumps.
What is their fate?
 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.