Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Once fusion reactions begin at the center of a cloud of gas, we call the object a star. For the bulk of its lifetime, a star fuses hydrogen into helium in its core. During this time, the star sits somewhere on the main sequence in the HR diagram: hot and luminous, if it is massive, or cool and dim, if it is a lightweight.
Let's take a look at the nuclear reactions which provide energy during the hydrogen-burning phase of its life.
As long as stars are on the main sequence, they turn hydrogen nuclei into helium. The output helium has a smaller mass than the input hydrogens.
mass of 1 proton p = 1.67358 x 10^(-27) kg mass of 4 protons 4p = 6.6943 x 10^(-27) kg mass of helium nucleus He = 6.6466 x 10^(-27) kg -------------------------------------------------------------- difference 4p - He = 0.0477 x 10^(-27) kg
The "missing" mass appears as energy, according to Einstein's famous equation E = mc^2. So, the net result of building one new helium atom is the release of
8 8
E = 0.0477 x 10^(-27) kg * (3 x 10 m/s) * (3 x 10 m/s)
= 4.3 x 10^(-12) Joules
It may be a tiny amount of energy per reaction, but a LOT of reactions take place each second inside the core of a star.
The most straightforward way to build a helium nucleus would seem to be a simultaneous collision of 4 protons:
Unfortunately, the chances that four protons all head in just the right direction to meet at the same point at the same time are very small. Moreover, since each proton has a positive charge, even if four protons did happen to move towards each other, their mutual electric repulsion would keep them from fusing together.
So how does the hydrogen turn into helium? It turns out that there are two series of reactions which can eventually bring about the same result.
The p-p chain is the main energy source in the Sun and stars which are less massive. It involves three steps:
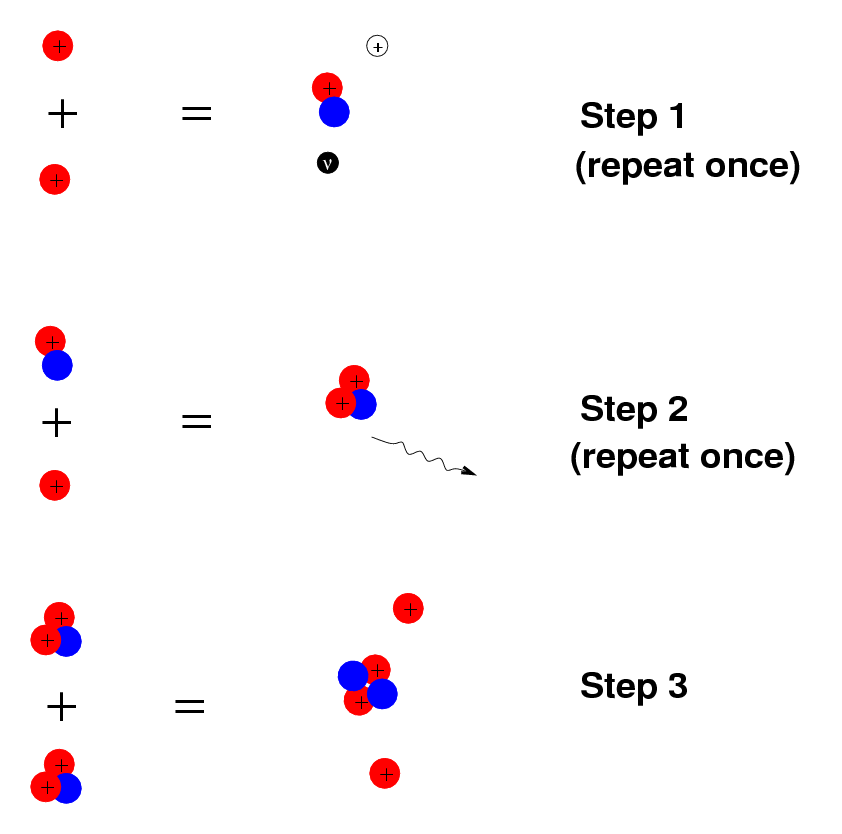
Only the first step requires bare protons fusing together. All the subsequent steps involve neutrons (shown as blue circles), which help to overcome the electric repulsion. Note that the first and second steps must take place twice, to generate the two nuclei of helium-3 which fuse in the final step. There are several variations on this basic process, but the version shown is the most common.
The p-p chain only works if the temperatures at the center of a star are high enough to throw particles together very hard. The critical value is around 10 million Kelvin. The amount of energy generated by the chain depends on the temperature: higher temperature causes more violent collisions, which more frequently lead to fusion. The rate of energy generation is something like
4
rate of energy production = (something) * T
Q: If the temperature at the center of a star
rises by 10 percent, how much more energy
is generated?
The CNO cycle is the main energy source in stars more massive than the Sun. It involves many steps, and the assistance of "heavy" nuclei:
As for the p-p chain, only the main branches of the cycle are shown above.
If the cloud from which a star forms contains only pure hydrogen, or hydrogen and helium, then the CNO cycle cannot take place: there won't be any Carbon, Nitrogen, or Oxygen atoms in the core. The very first generation of stars to form after the Big Bang contained no "heavy" elements, and so could not have generated energy in this manner.
The CNO cycle requires slightly higher temperatures than the p-p chain; it produces very little energy below about 16 million Kelvin. The central temperature of the Sun is just below this critical value, around 15 million Kelvin. Only stars with masses higher than our Sun reach such temperatures in their cores.
Once the CNO cycle does start to run, it is very sensitive to temperature. The rate at which it generates energy can be written as
20
rate of energy production = (something) * T
Q: If the temperature at the center of a star
rises by 10 percent, how much more energy
is generated by the CNO cycle?
To sum it up, if you where a star falls on the HR diagram, then you know what sort of nuclear reactions are taking place deep within its interior:
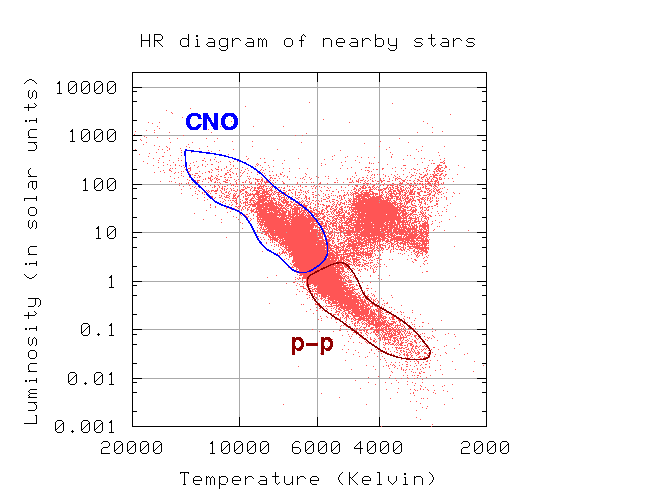
Because they are so sensitive to changes in temperature, both the p-p chain and the CNO cycle act as stellar thermostats. Changes in the rate of energy production can cause the layers of gas above the core to expand outwards, or shrink inwards. But at the same time, it is the gravitational pressure of these overlying layers of gas which produce the high temperatures required for the fusion reactions. The result is a delicate balance which tends to restore itself to equilibrium.
You can show that if the central temperature rises a little for some reason, a similar series of actions will cause the core to expand a bit, dropping the temperature back towards its original value.
In short, the combination of the energy generated by fusion reactions pushing outwards and gravitational force pulling gas inwards leads to a stable equilibrium. As long as a star has hydrogen in its core to fuse, it will maintain a roughly constant central temperature; which means it will generate a roughly constant amount of energy; and that means it will shine with a roughly constant luminosity. Its position in the HR diagram (based on luminosity and photosphere temperature) won't change much at all during its long phase of hydrogen burning.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.