
 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Geologists know that the Earth is very, very old. Mountains rise up as tectonic plates slide into each other, and rivers cut channels through the mountains, carrying the sediment out to sea. It all takes a great deal of time. By the turn of the twentieth century, geologists were confident that the Earth was billions of years old.
It seems reasonable that the Sun is just as old as the Earth, if not older. So the Sun is also billions of years old.
We can easily measure the luminosity of the Sun: the amount of energy it radiates into space each second. To a rough approximation, the luminosity of the Sun is about
Here is where the cleverness comes in: suppose that the Sun really were filled with ordinary flames, produced by an ordinary chemical combustion. For example, suppose that the Sun was a mixture of gasoline and oxygen, burning away merrily. We understand how this chemical reaction works: burning gasoline will produce about
Let's ask two questions: first, how fast would the Sun have to burn its fuel?
Q: How many kg of gasoline would the
Sun have to burn each second to
produce its current luminosity?
The second question is, how long could the Sun last at this rate?
Q: Assume that the entire mass of the
Sun, 2 x 10^(30) kg, was gasoline,
and ignore the required oxygen.
How long could the Sun continue to
burn at its current rate?
Express your result in seconds,
and in years.
Gosh, that's not going to work. The Sun cannot be powered by the burning of gasoline. In fact, no chemical reaction known to man will produce enough energy per kilogram to power the Sun for its apparent lifetime.
So, what IS powering the Sun?
We believe that stars are born inside giant molecular clouds. A single cloud is large enough to create hundreds or thousands of stars, as this picture of the Orion Nebula makes clear:

After the stars are born, their intense radiation ionizes and then disperses the remaining gas. The result is a group of young stars all born at roughly the same time and in the same place. We call these collections of sibling stars open clusters.
One of the nearest and brightest of the open clusters is the familiar Pleiades.

Credit and Copyright:
Robert Gendler
If we measure the apparent magnitude of the stars in this cluster through several filters, we can make an HR diagram of the stars in the cluster. Because all the stars are at the same distance from us, we can substitute their apparent magnitudes (easy to measure) for their absolute magnitudes (hard to calculate). Sometimes astronomers call this a color-magnitude diagram, since we are plotting apparent magnitude against color.
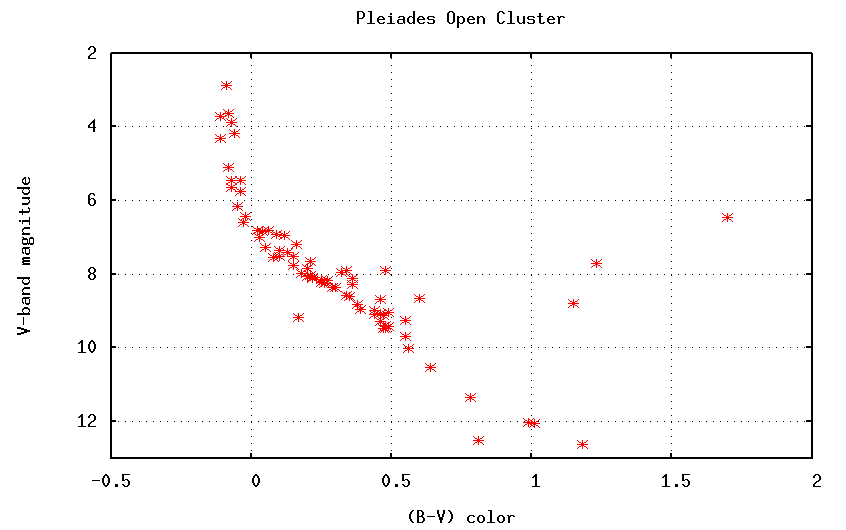
Note the clear main sequence and very small population of giant stars.
Q: What is the (B-V) color of the
hottest stars on the main sequence?
We can make HR diagrams for other open clusters, too. Look closely at two features of each:

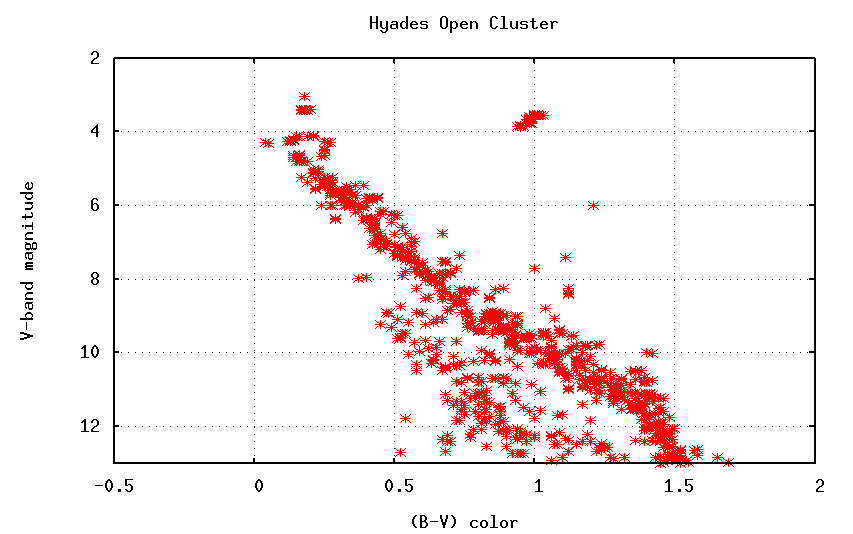
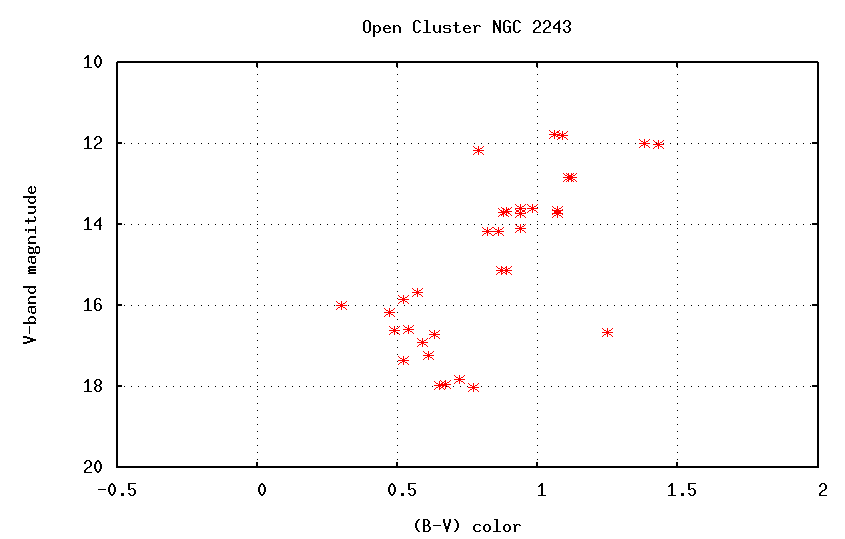
There appears to be a pattern: the reddish stars on the main sequence are always present, but the bluest stars appear to be missing from most clusters. And, as the blue stars disappear, the giant branch becomes more and more prominent. Could it be that the bluest, most luminous stars are turning into red giants?
We know from measurements of double stars that the main location of a star on the main sequence depends on its mass: high mass stars are blue, hot and luminous -- near the "top" of the main sequence -- while low mass stars are red, cool and feeble -- near the "bottom" of the main sequence.
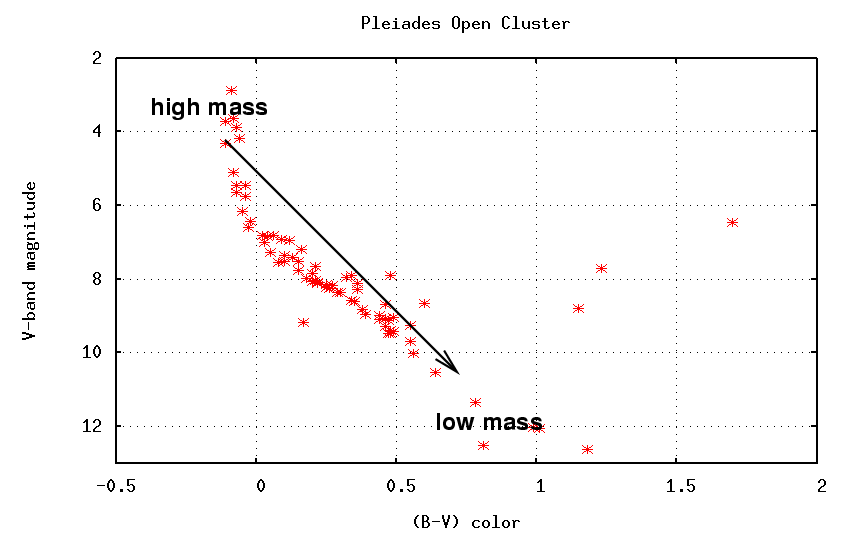
We can explain the appearance of the color-magnitude diagram of different open clusters if the high-mass stars are the first to evolve off the main sequence and turn into red giants, while the low-mass stars remain on the main sequence for long periods of time. If this is true, then the Pleiades must be a young cluster ....
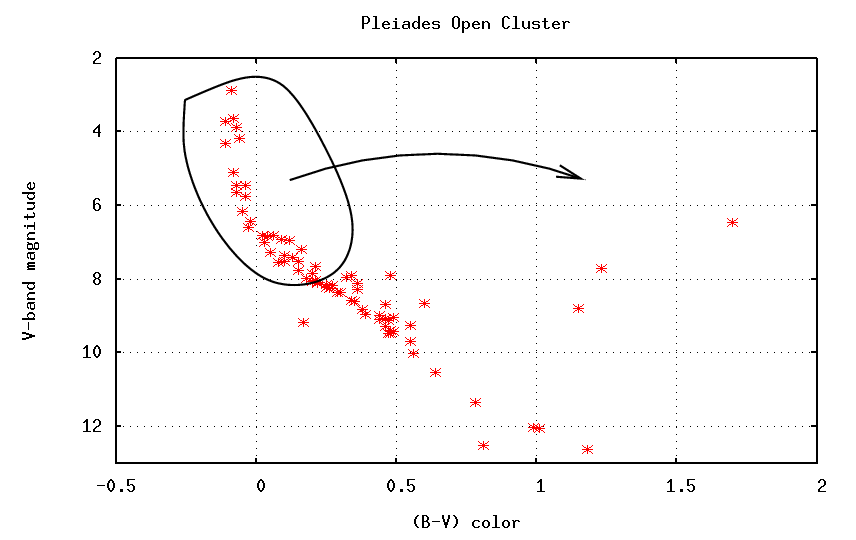
... and NGC 2243 must be an old one.
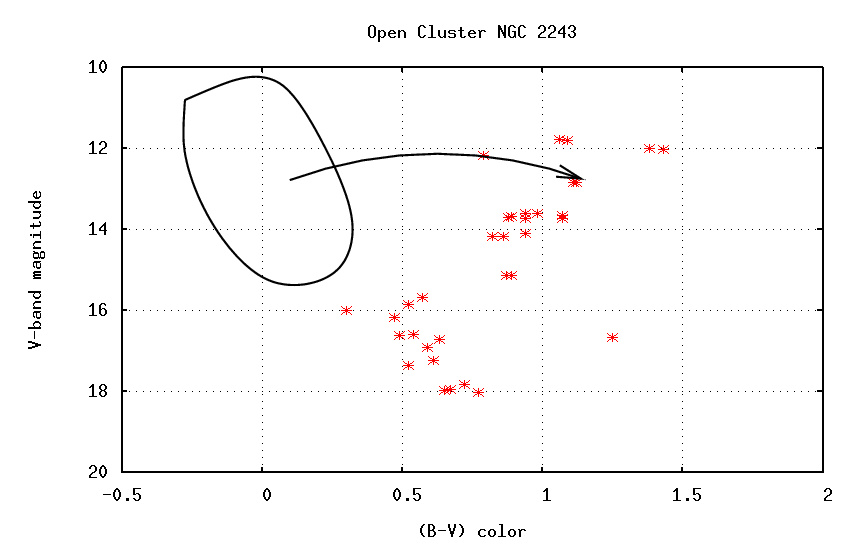
This would suggest that the power source inside a star depends on the mass of the star: massive stars must be using up their fuel much more rapidly, since they start with more fuel but run out of it long before low-mass stars do.
In the 1920s and 1930s, physicists realized that there was a source of energy which was MUCH more efficient than ordinary chemical reactions: nuclear fusion. Fusion involves the conversion of several lightweight atomic nuclei into a single, more massive nucleus. For example, 4 hydrogen nuclei (protons) can fuse to form 1 helium nucleus(*):
(*) Yes, the fusion also creates two positrons, but their mass is small compared to the difference shown below.
mass of 1 proton p = 1.67358 x 10^(-27) kg mass of 4 protons 4p = 6.6943 x 10^(-27) kg mass of helium nucleus He = 6.6466 x 10^(-27) kg -------------------------------------------------------------- difference 4p - He = 0.0477 x 10^(-27) kg
The "missing" mass appears as energy, according to Einstein's famous equation E = mc^2. So, the net result of building one new helium atom is the release of
8 8
E = 0.0477 x 10^(-27) kg * (3 x 10 m/s) * (3 x 10 m/s)
= 4.3 x 10^(-12) Joules
It may be a tiny amount of energy per reaction, but is represents a very large amount of energy per kilogram of initial hydrogen fuel.
Q: The equations above show that 6.69 x 10^(-27) kg
of input hydrogen fuel will produce
4.3 x 10^(-12) Joules of energy.
How much energy would 1 kg of hydrogen produce?
How does that compare to the energy produced
by burning 1 kg of gasoline? Recall that
1 kg of gasoline produces about 45 million Joules.
Nuclear reactions are extremely efficient. They can provide enough energy for every kilogram of fuel to power the Sun for its entire 4.6-billion year life, and continue to do so for billions of years to come.
There are several ways in which hydrogen can be converted into helium. The simplest conversion process, and the one which provides most of the energy in the Sun, is called the p-p chain. It involves three steps:
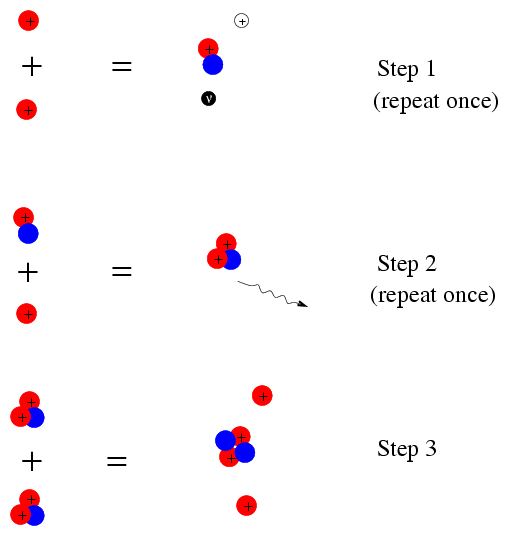
Only the first step requires bare protons fusing together. All the subsequent steps involve neutrons (shown as blue circles), which help to overcome the electric repulsion. Note that the first and second steps must take place twice, to generate the two nuclei of helium-3 which fuse in the final step. There are several variations on this basic process, but the version shown is the most common.
The p-p chain only works if the temperatures at the center of a star are high enough to throw particles together at very high speeds. The critical value is around 10 million Kelvin.
We know that some clouds of gas and dust do form stars. The very center of a dense cloud may undergo a runaway gravitational gravitational collapse, as discussed in the previous lecture.
But we can now add to that description a new factor: as particles of gas fall inward, they gain kinetic energy. You may recall from a chemistry or physics class that the speed of particles in a gas determines its temperature. So, we can write the star-formation process with an extra step:
When the temperature in the center of this dense little clump reaches 10 million degrees, fusion reactions begin. They supply energy to the surrounding gas to increase the pressure, which halts the gravitational collapse. We call stars which have just reached this stage -- the start of hydrogen fusion in their centers -- Zero Age Main Sequence stars, or ZAMS for short.
The amount of energy generated by the chain depends on the temperature: a higher temperature causes more violent collisions, which more frequently lead to fusion. The rate of energy generation is something like
4
rate of energy production = (something) * T
Q: If the temperature at the center of a star
rises by 10 percent, how much more energy
is generated?
Aha! This explains why the more massive stars evolve more quickly. At the center of a massive star, the temperature is higher than in a low-mass star, so the rate of nuclear reactions is higher, and so the star runs through its initial allotment of hydrogen more quickly.
In fact, once they understand the details of the nuclear reactions at the centers of stars, astronomers can build computer models of stellar evolution. They break a star into shells within which the temperature, density, chemical composition, etc., are uniform.
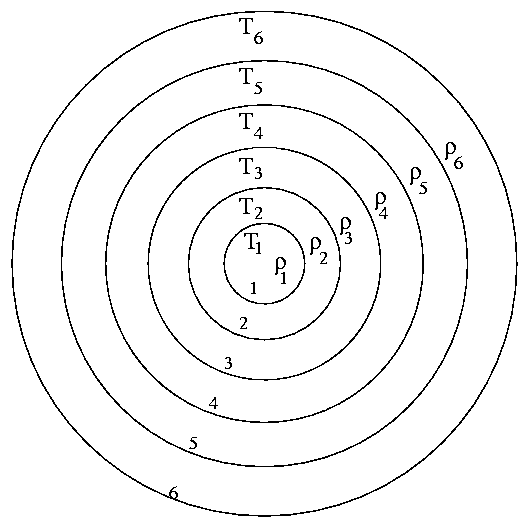
Then, within each shell, they compute the rate at which nuclear reactions occur and produce energy, and the rate at which that energy flows outwards to other shells. It involves a LOT of calculations, but computers are fast enough to follow the evolution of an entire star over its entire lifetime.
The stellar models confirm that the most massive stars are the first to run out of hydrogen in their cores and evolve off the main sequence.
 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.