 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Our final journey to Interference-Ville will involve the interaction of light which has travelled through MANY slits in a wall.
Let's warm up a bit before we go for the big time.
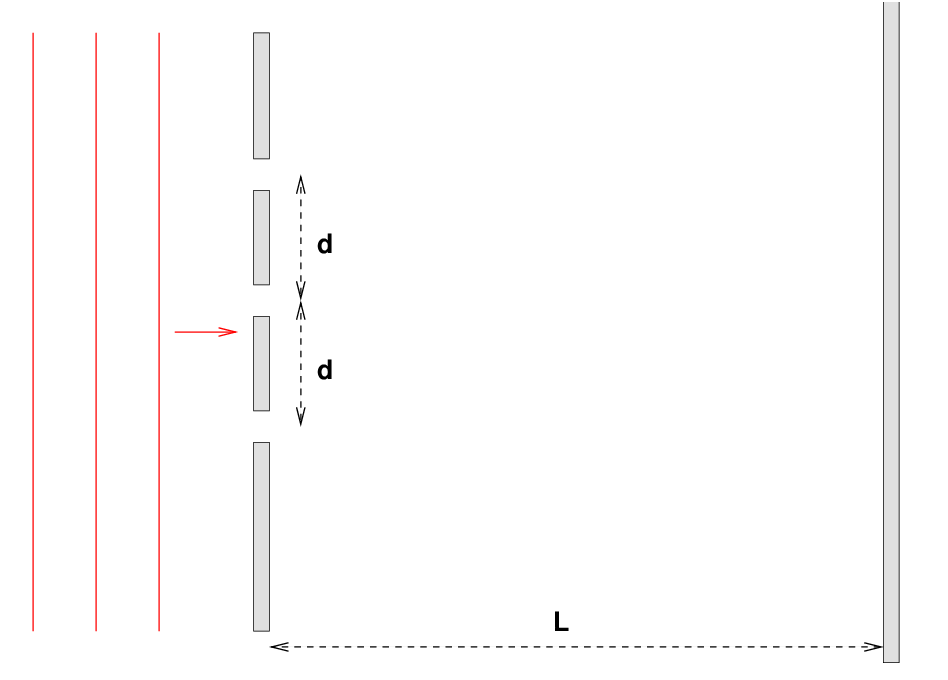
Waves travel from left to right toward a wall, which has THREE small slits, separated by identical distances d. On the other side of the wall is a large empty space; only after travelling a distance L will any waves reach a second wall.

Again, we require that the waves approaching the left-hand wall be coherent: they must all have the same wavelength and present the same phase all the way across the single slit. One way to make this happen is to place a single source of waves far, far to the left of this wall, so that it lies in the plane wave regime of that source.
The big question is: what happens to any waves which travel through the three slits?
We can follow the same type of analysis you have seen before for two slits, by computing the extra distance travelled by the waves from each slit relative to the first. Waves from the middle slit must travel an extra distance x = d sin(θ), and those from the top slit must travel an extra 2x = 2d sin(θ). Here, as before, the angle θ is equal to the distance y away from the center of the distance screen at which the waves meet.
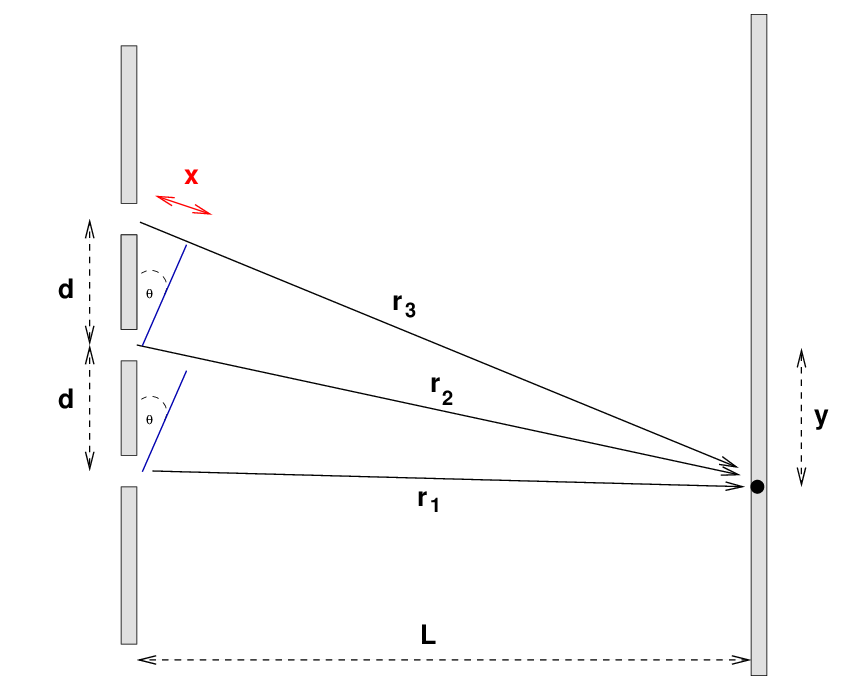
Now, as before, we can write an equation for each wave which involves the radial distance r between its slit and the point P, and the time t. Where the waves meet at point P, the sum is

Once again, we can assume that if d ≪ L, all the radial distances are nearly the same, so we can use an average radial distance to divide the amplitude. We can also replace the terms like kr inside the sine functions with an equivalent phase offset. In this case, the phase offset is
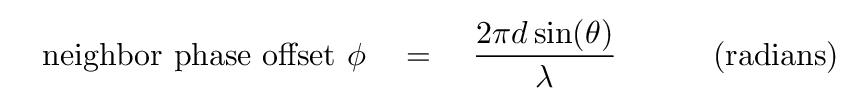
Using this new variable, the sum is
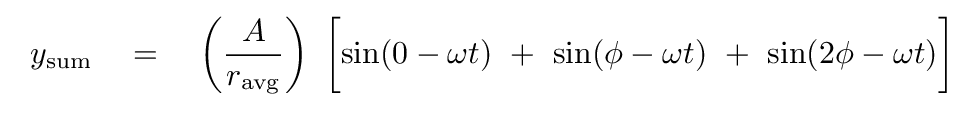
Hmmm. Can we simplify this expression?
Yes, if we use one of the trig identities:
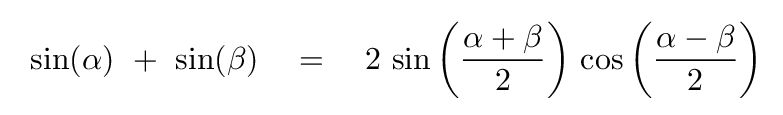
If we use apply this to the first and third of the sine functions -- leaving the middle sine term alone for the moment -- we find
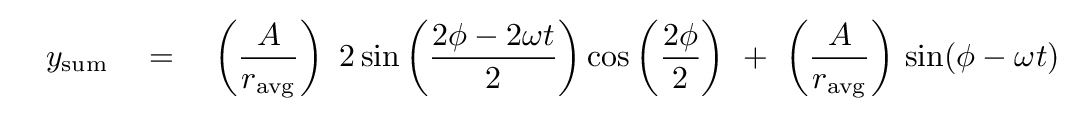
Q: Can you simplify this?
Sure! Pull out a factor of sin(φ - ωt) and cancel some excess 2s, and you should get
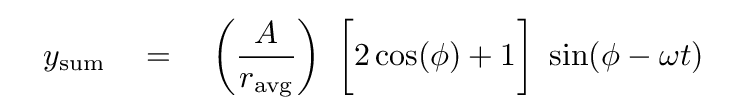
Now, the intensity of a wave is proportional to its amplitude squared, so the intensity of the sum is
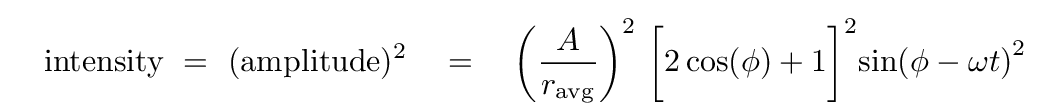
The sine-squared term at the end oscillates with time. If we create an average value over a long time, that yields a value of 1/2. So, we can say that the time-averaged intensity of the sum of three waves is
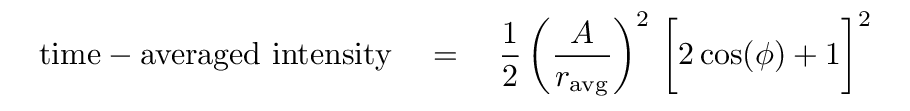
How does the pattern of intensity created by two slits compare to that created by three slits? Let's ignore, for now, the effects caused by the non-zero width of each individual slit.
In that case, the two-slit interference pattern has intensities which vary in a very simple way; as the square of cosine(φ/2), in fact.
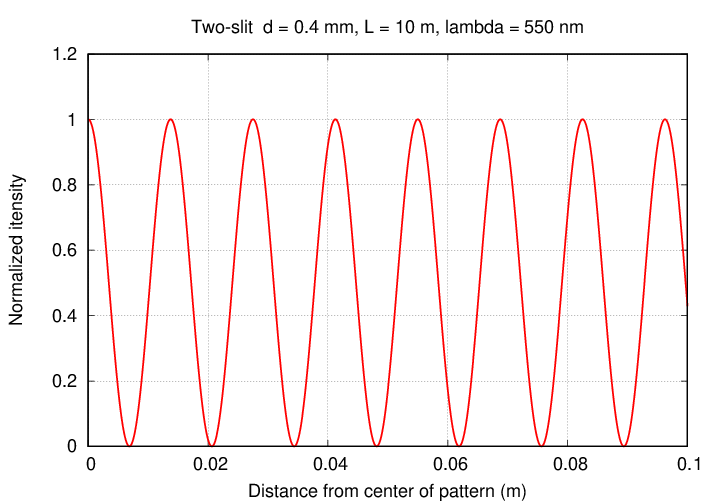
The three-slit intensity looks both similar and different.
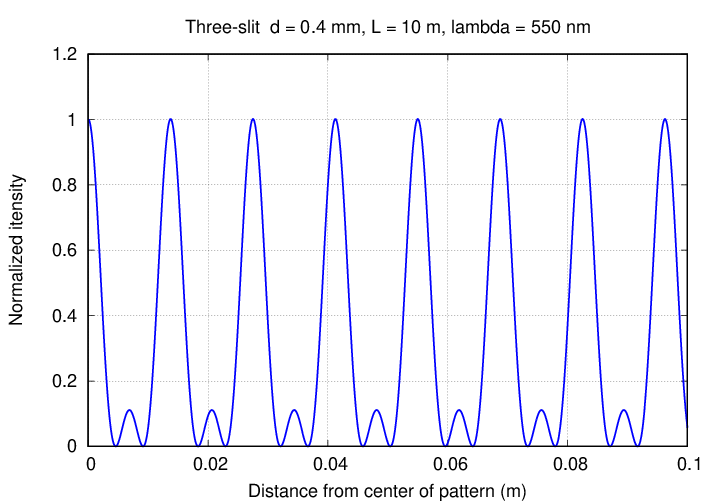
Q: How are the two patterns similar? Q: How are the two patterns different?
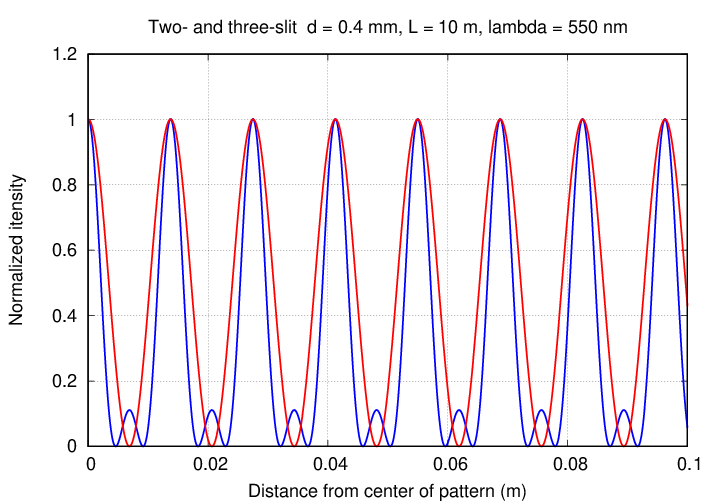
Why do the central peaks become more narrow? Well, when there were two slits, if the angle θ to some location on the wall was almost, but not quite, correct for perfect constructive interference, two waves would meet slightly out of phase. But now, with three slits, at that same not-quite-perfect angle, two waves are again slightly out of phase ... AND now a third wave is MORE out phase. When we combine all three waves, the result is a somewhat smaller total amplitude.
Why are there small peaks between the big ones? Those represent positions on the distant screen where the waves from the top and bottom slits interfere constructively ... but the waves from the middle slit, with just half that phase difference, are out of phase with each of the others. Having extra slits means that there are opportunities for SOME, but not all, of the waves to meet in phase.
The issue at hand is adding together waves which have
Adding just 2 waves isn't very difficult; we used a handy trig identity.
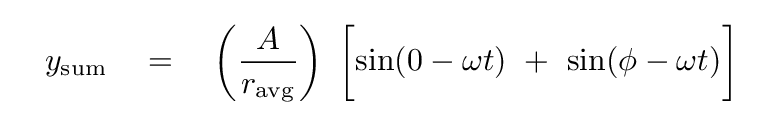
Adding together 3 waves is harder. We ended up using a similar trig identity, but the result was a more complex equation.
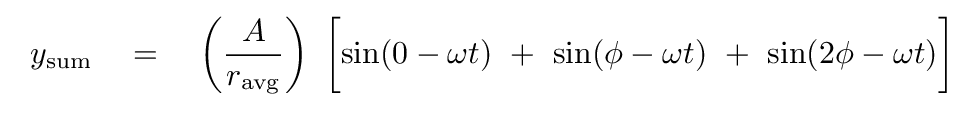
But trying to add 4 (or 5, or 6, or 10) waves using these methods grows more difficult very quickly.
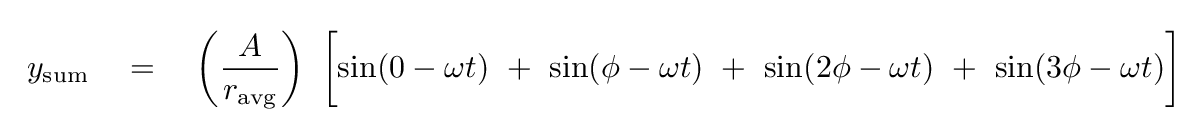
Fortunately, some clever people figured out another way to add together waves with identical frequencies, but different phases. That method involves entities called phasors.
For our purposes, the method boils down to this: to add together N waves, each offset from its neighbor in phase by φ
For example, to add two waves offset by phase φ = π/4 rad, we draw the following diagram:
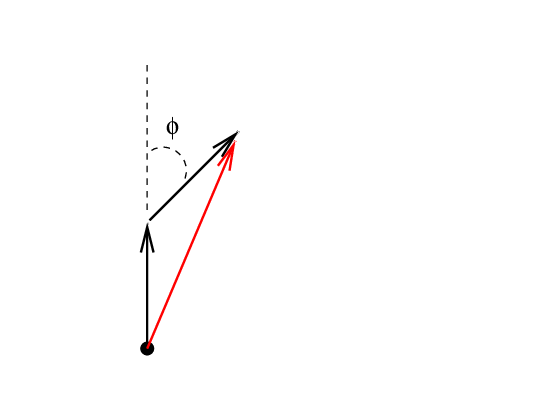
To add three waves, each offset by φ = π/4 rad from its neighbor, we draw this:
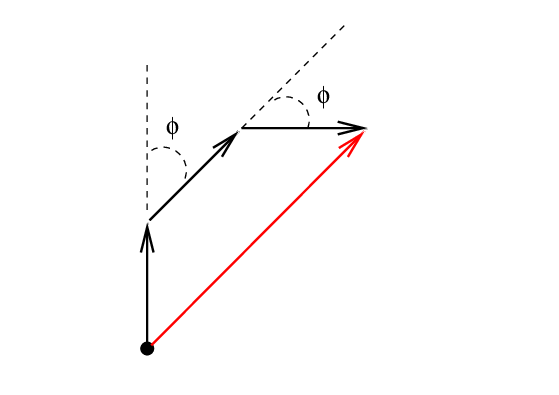
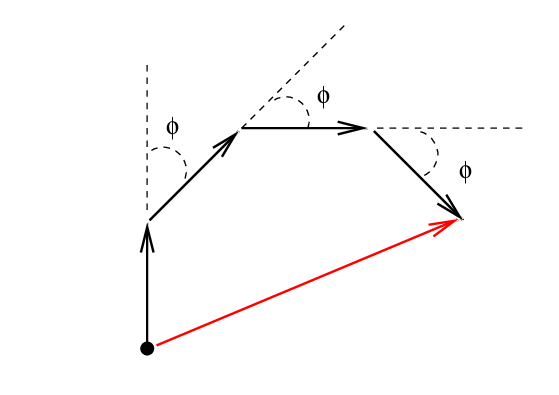
If there are four waves to add, we just keep adding arrows to the end of the construct:
Consider waves from 2 slits interfering. The possibilities for phase offset run from 0 to 2π. There are three special cases, which give us, respectively
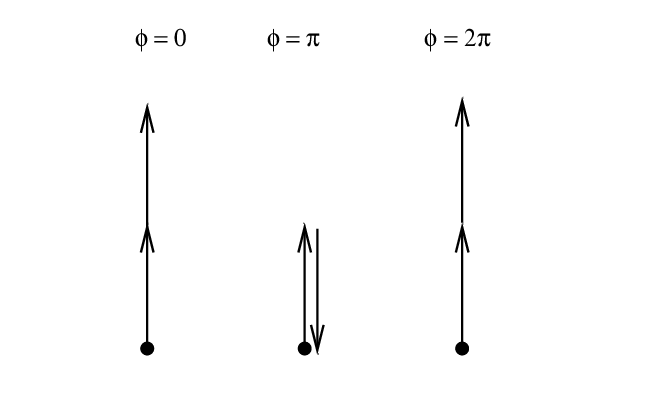
Q: What is the AMPLITUDE of each summed wave?
Q: What is the INTENSITY of each summed wave?
Q: What is the intensity of each summed wave,
relative to the intensity of the φ = 0 case?
Hmmm.

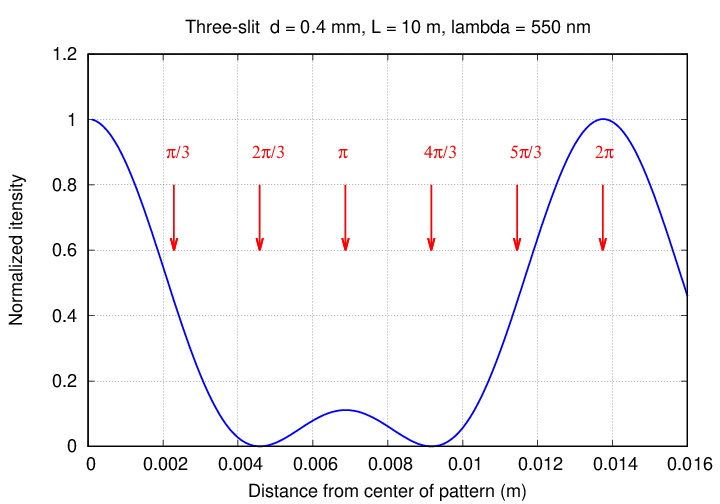
Suppose we add waves from 3 slits; that means we need to draw 3 phasor arrows, tip to tail. In this case, there are five phase offsets φ of particular interest:
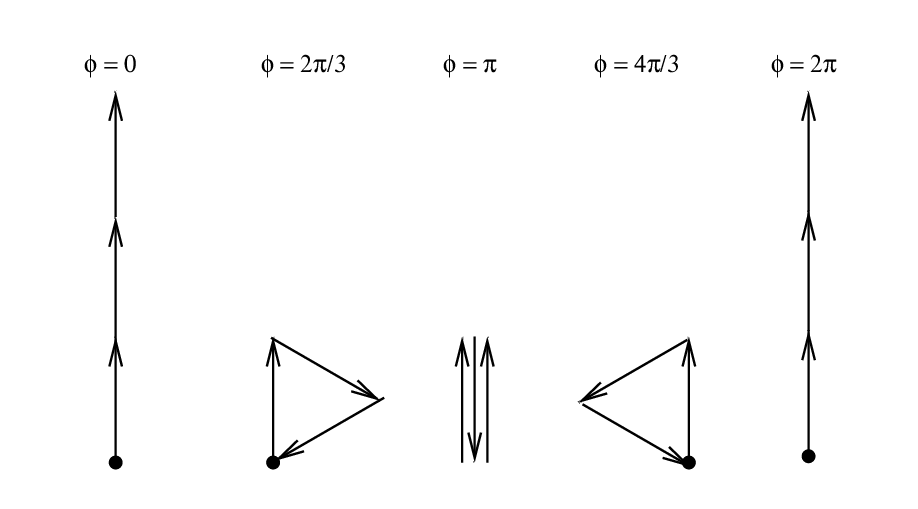
Q: What is the AMPLITUDE of each summed wave?
Q: What is the INTENSITY of each summed wave?
Q: Express the intensity of each summed wave,
RELATIVE to the intensity of the φ = 0 case.
Can you identify the locations on the three-slit interference pattern that correspond to each of those cases?

Maybe it will be easier to see on a closeup near the center.
One can use phasors to create a geometric proof, of a sort, that shows that when one adds together N waves, each offset from the next by φ radians in phase, the sum will have an amplitude given by
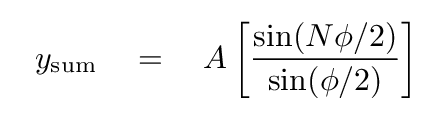
So, the general formula for the sum of waves passing through N identical slits, each separated by distance d from its neighbors, is
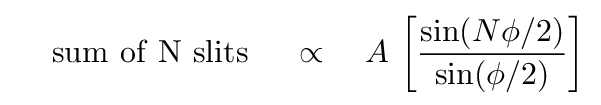
where the phase offset φ between the waves of neighboring slits is
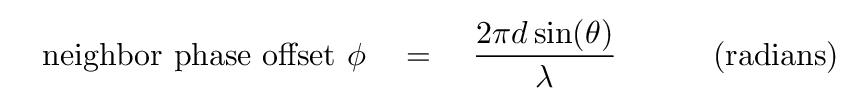
and θ is the angle away from the center of the distant screen where the waves meet.
Let's see what happens as we increase the number of slits. When N = 4, the intensity on the distant screen looks like
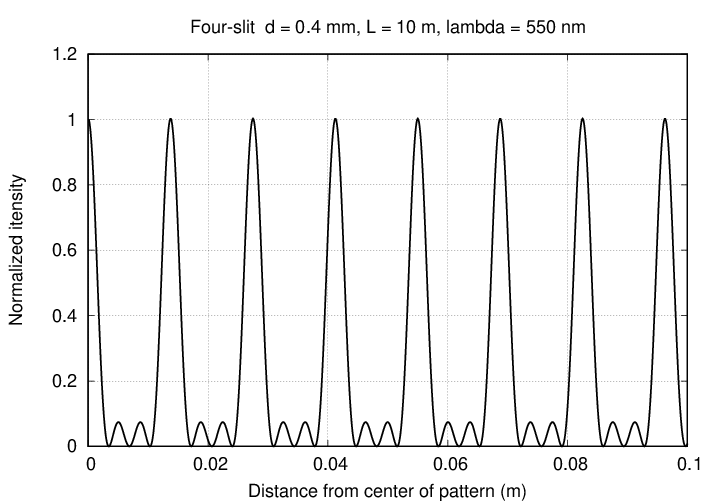
Comparing the patterns for N=2 and N=4
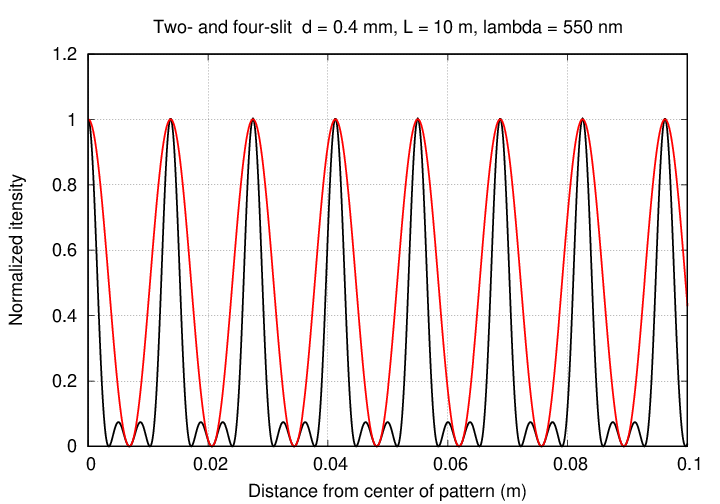
reveals a continuation of the changes we noted earlier:
These trends continue as we increase the number of slits to N=10.
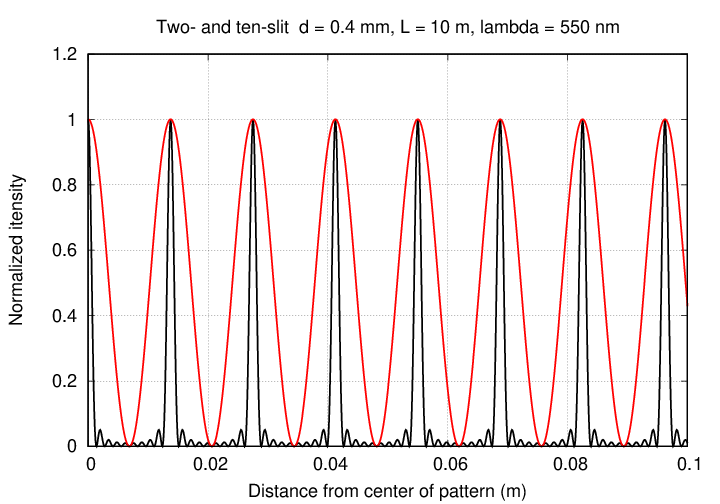
Why do the peaks become more and more narrow? Well, consider what happens to waves from the first to the last slit in the entire sequence. If the angle θ is EXACTLY right, so that
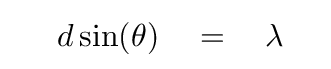
then 2 times this extra distance will still be an integer number of wavelengths; and the same for 3 times the extra distance, 5 times the extra distance, or 100 times the extra distance: the interference will always be constructive.
But what if the angle is off by just a little bit? Then the difference between neighboring slits will be one full wavelength, plus a little extra ε.
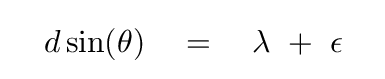
If there are just two slits, the difference in phase between the first slit and the second slit will be just that little extra; as long as it is small compared to the wavelength, the two waves will still interfere (almost) perfectly constructively.
If there are 10 slits, though, then the difference adds up: as we move from one slit to the next to the next, we add one more extra amount ε to the difference in distance travelled. By the time we get to the final slit, waves must travel 10 full wavelengths (that's good), plus 10 times ε extra (that's bad).
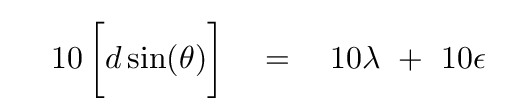
That extra distance might add up to a significant fraction of one wavelength, which means that this wave is no longer in phase with the first wave.
The more slits we add, the more out-of-phase waves from the distant slits become. That means that even a tiny difference in angle from the PERFECT angle will lead to lots of destructive interference from many slits; and that means that the intensity at positions between the PERFECT angles will be close to zero.
Opticians and physicists and astronomers and chemists and scientists of all types find it very convenient to be able to separate light of different wavelengths; the whole field of spectroscopy requires that one can somehow cause light of one wavelength to go in a different direction than light from another wavelength.
For example, if we can break the light of a star into a spectrum
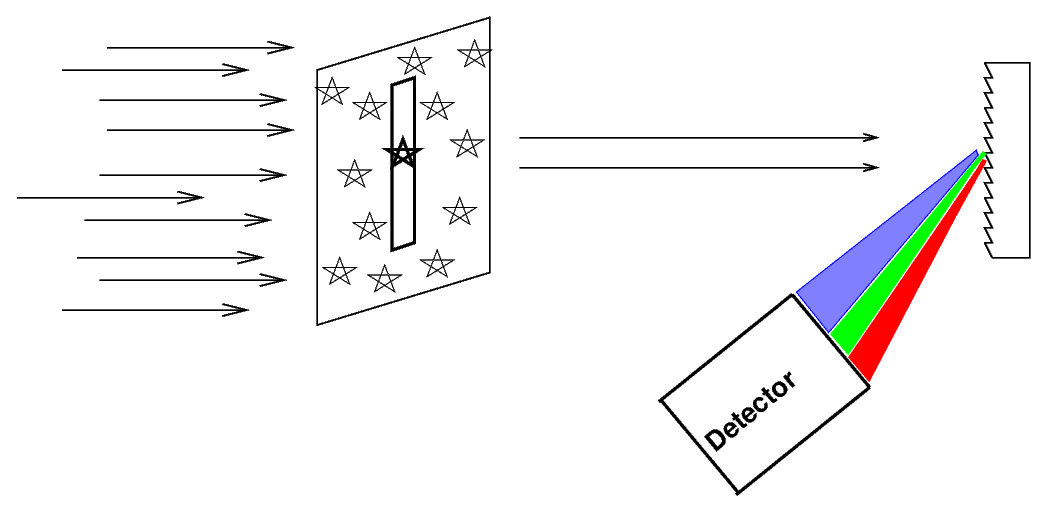
then one can detect both large-scale and small-scale features, which can in turn reveal the temperature, chemical composition, radial motion, and other features of the star.
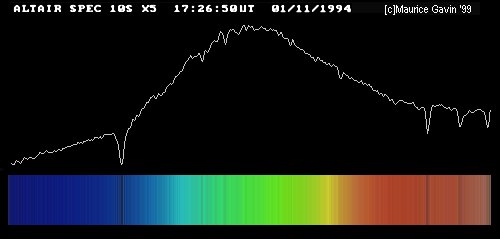
Image courtesy of
Maurice Gavin and the wpo-amateur spectroscopy site.
A diffraction grating is a great tool for this job. If one scribes a large number of parallel grooves into a reflective surface of glass or metal, or into a thin sheet of transparent material like plastic, then the grooves will act like tiny slits. Light bouncing off, or passing through, the material, will interfere with itself. Remember that constructive inteference will occur when the phase offset
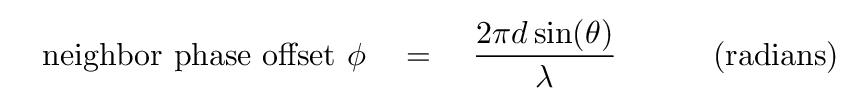
is exactly 2π radians. That means that light of different wavelengths λ will create bright peaks at different angles θ away from the center of the system.
 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.