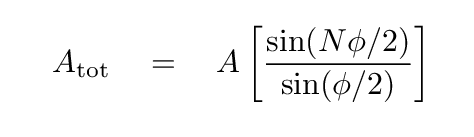
 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Our goal here is to derive the formula for the amplitude Atot of the sum of N waves, each of amplitude A and offset from its neighbor in phase by an angle φ. We want to end up with
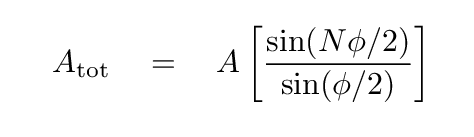
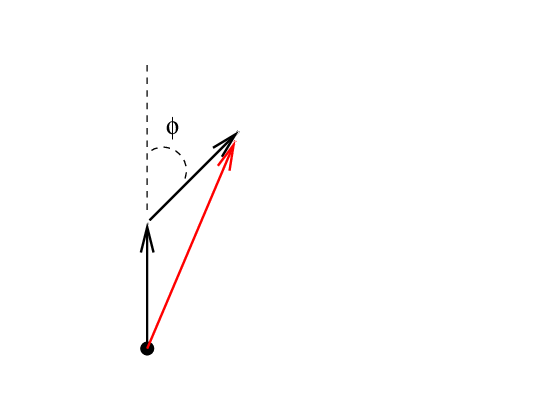
Remember how phasors work. In order to add just TWO waves, each of amplitude A, but offset in phase by some angle φ, we draw TWO vectors, head to tail, changing the direction of the second vector by an angle φ.
So in order to add N waves, we must draw N vectors, head to tail, changing the direction of each vector by an angle φ from the previous vector.
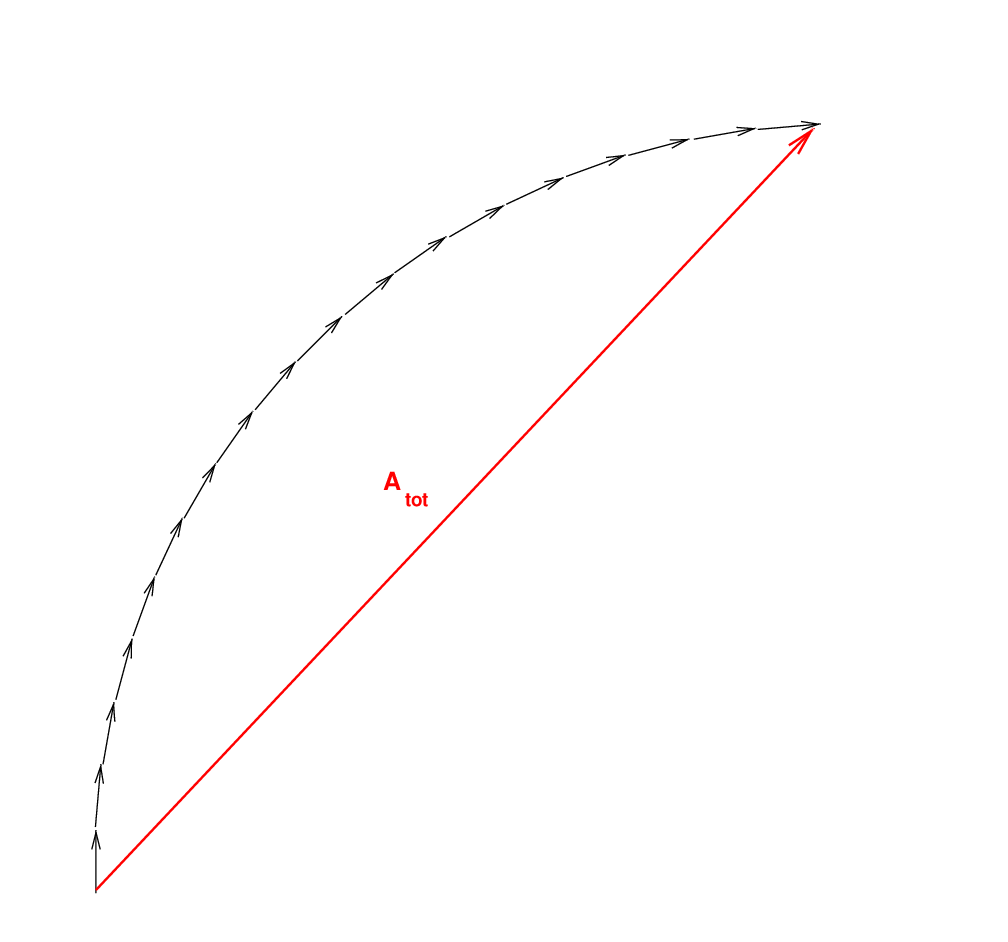
The amplitude of the resultant vector is Atot. How does it compare in size to the length of each component vector, A?
To answer this question will take several steps, and a bit of geometry. We'll begin by drawing portions of the circle which is inscribed by the N vectors; the radius of this circle is some length R. We don't know how R is related to A, but don't worry -- it will cancel out of our final expression. The angle subtended by this arc is α, and the length Atot is a chord stretching across this arc.
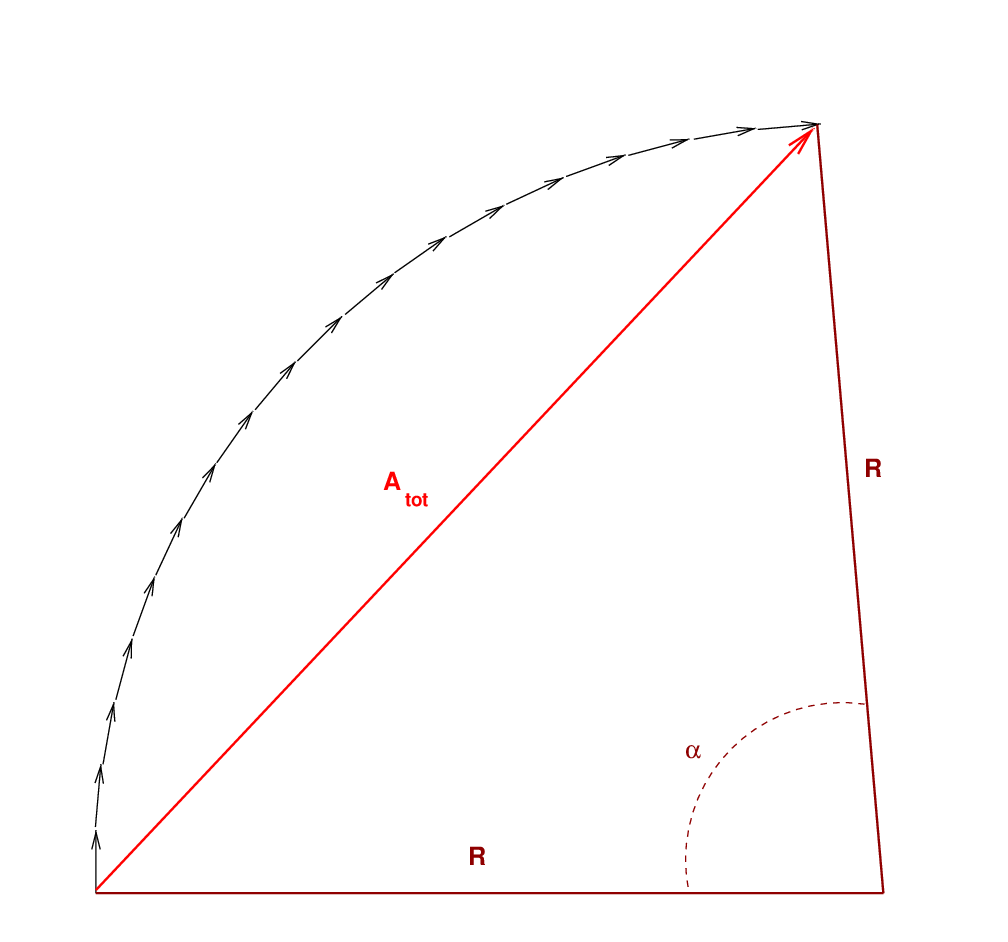
Next, we bisect the angle α, creating two right triangles. Each right triangle has a hypotenuse of length R, a side of length Atot/2, and an angle of size α/2.
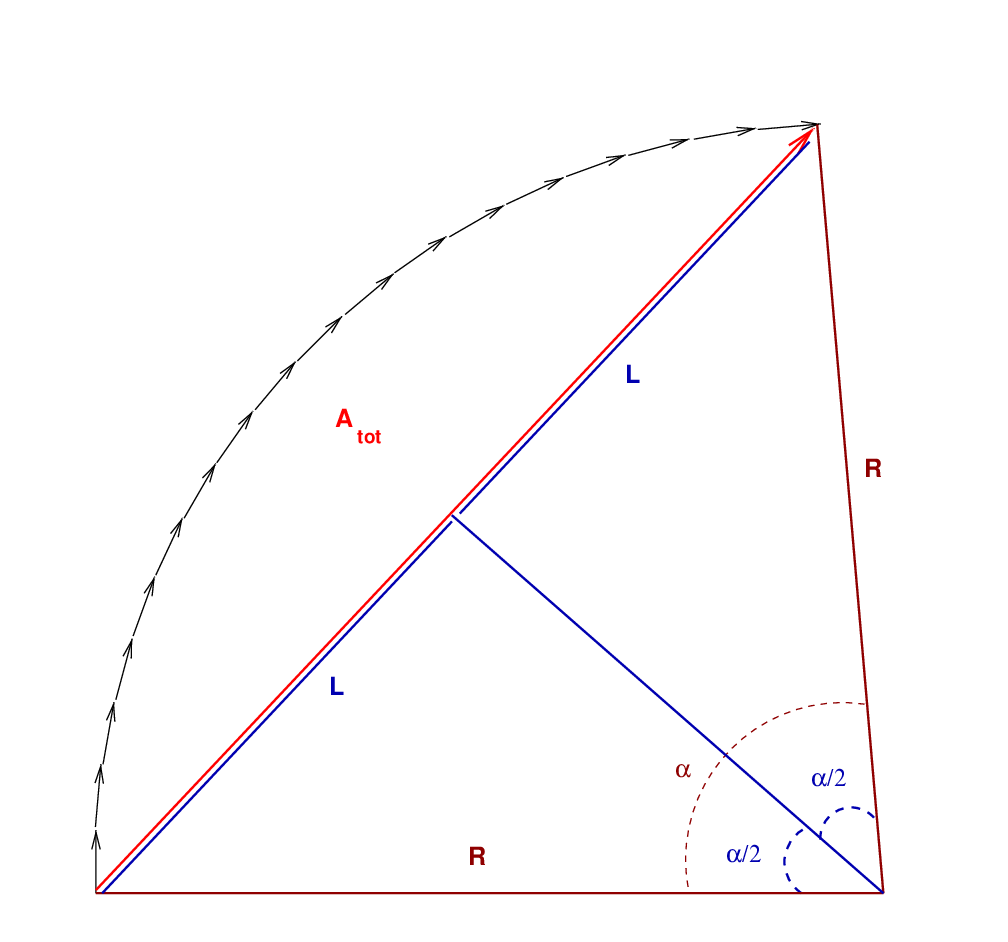
Trigonometry tells us that the length L is
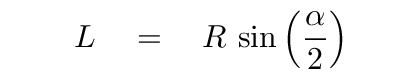
and therefore the amplitude of the summed waves is
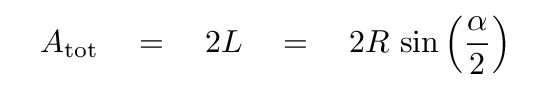
Right. Let's save that for the moment.
If we look at just one of the component vectors as a portion of the entire arc, we can see that it subtends only a small angle φ.
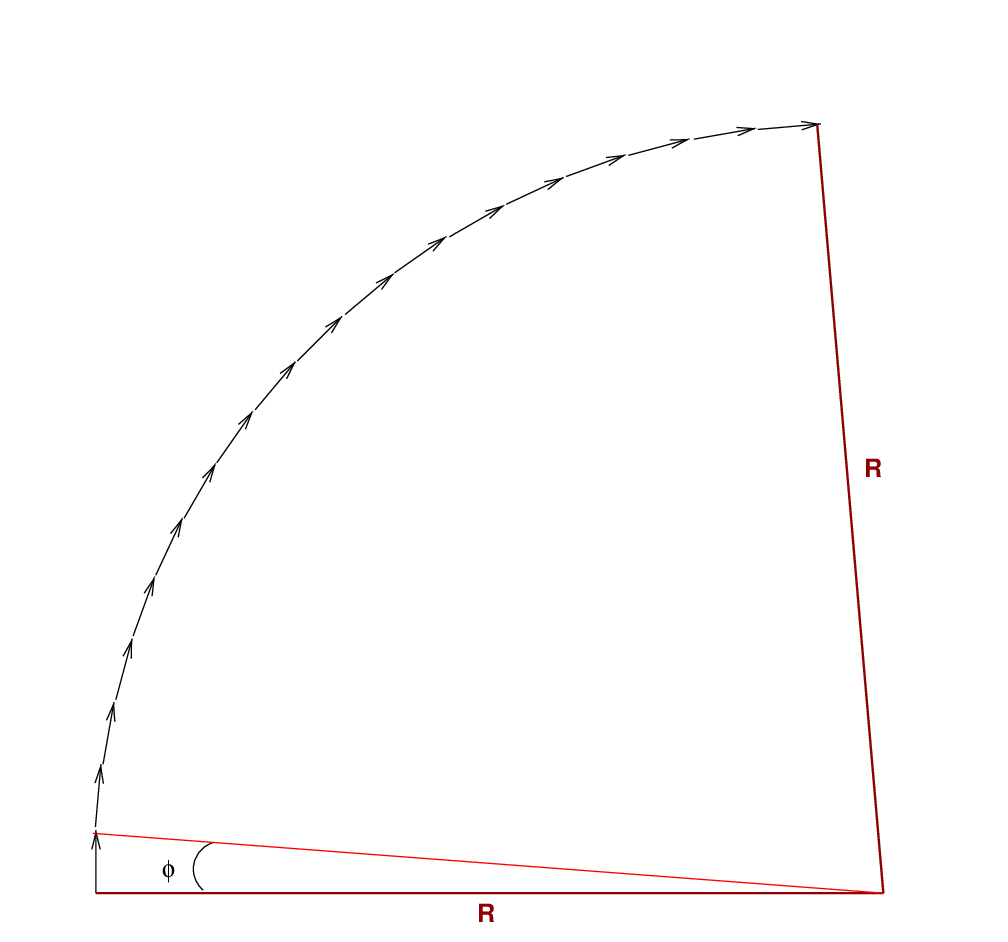
If we zoom in on this little section of the diagram, we can create two very skinny right triangles by bisecting the angle φ.
 Using these skinny triangles,
we see that the short end of each one, M, is half the
length of A.
Using these skinny triangles,
we see that the short end of each one, M, is half the
length of A.
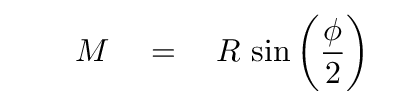
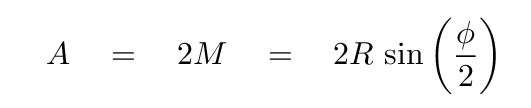
Okay. Now we can compare the amplitude of the sum of the N phasors with the sum of a single phasor.
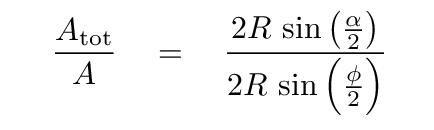
We're almost there! The final step in our demonstration is to find a connection between the big angle α, subtended by Atot, and the little angle φ, subtended by A. But there is a simple relationship; just look:
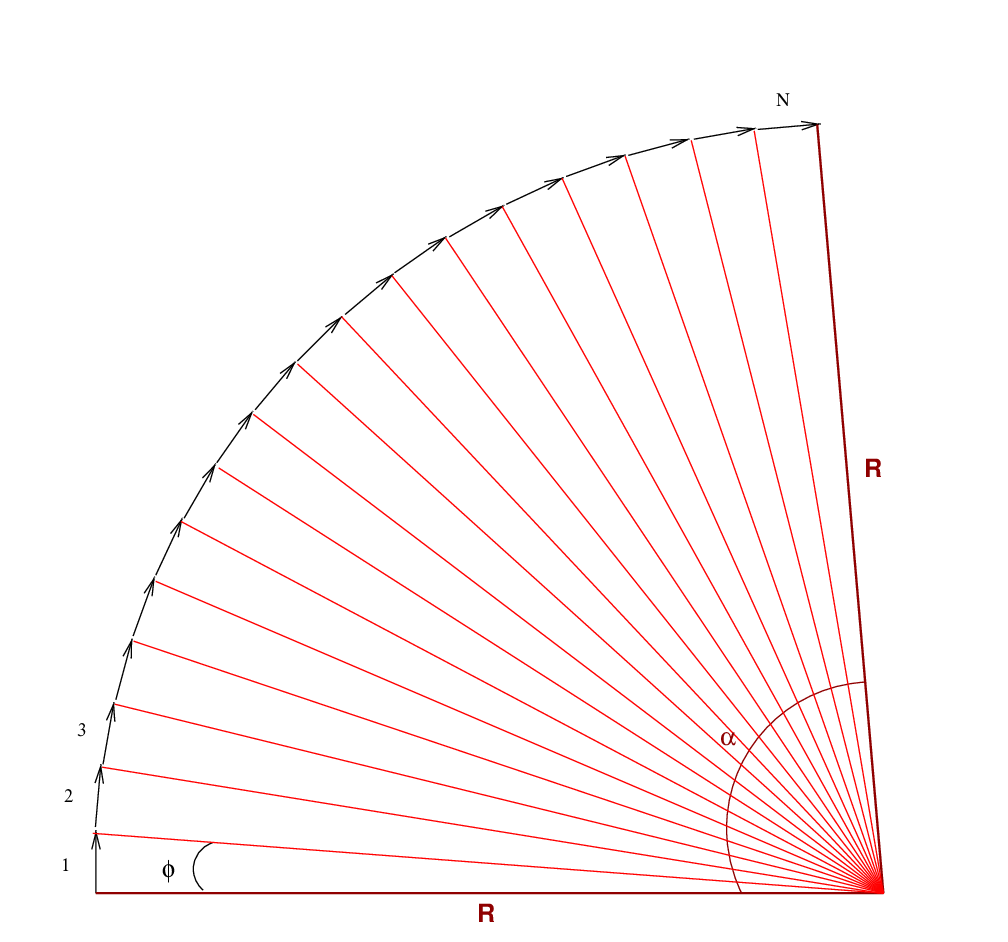
The angle α is simply N times the angle φ.
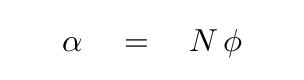
That means we can write the ratio of the lengths as
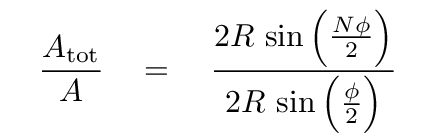
And thus, the amplitude of the sum of N waves must be
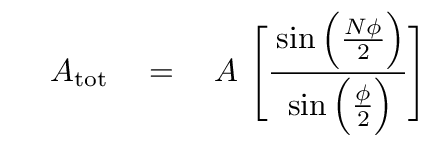
QED.
 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.