Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Today, we look at the interference of waves emitted by two slits in one wall, as the waves travel across an empty space and eventually impinge upon a distant wall. You may have seen this material in other classes, but the approach we take here will probably be somewhat different.
Waves travel from left to right toward a wall, which has two small holes or slits spaced a distance d apart. On the other side of the wall is a large empty space; only after travelling a distance L will any waves reach a second wall.
One of the conditions we impose upon this experiment is that the waves approaching the first wall must be coherent: they must all have the same wavelength and present the same phase at both slits. One way to make this happen is to place a single source of waves far, far to the left of this wall, so that it lies in the plane wave regime of that source.
The big question is: what happens to any waves which travel through the slits?
Our approach today will be to apply Huygens' Principle to the situation. Each of the holes in the first wall will act as sources of a new set of waves.
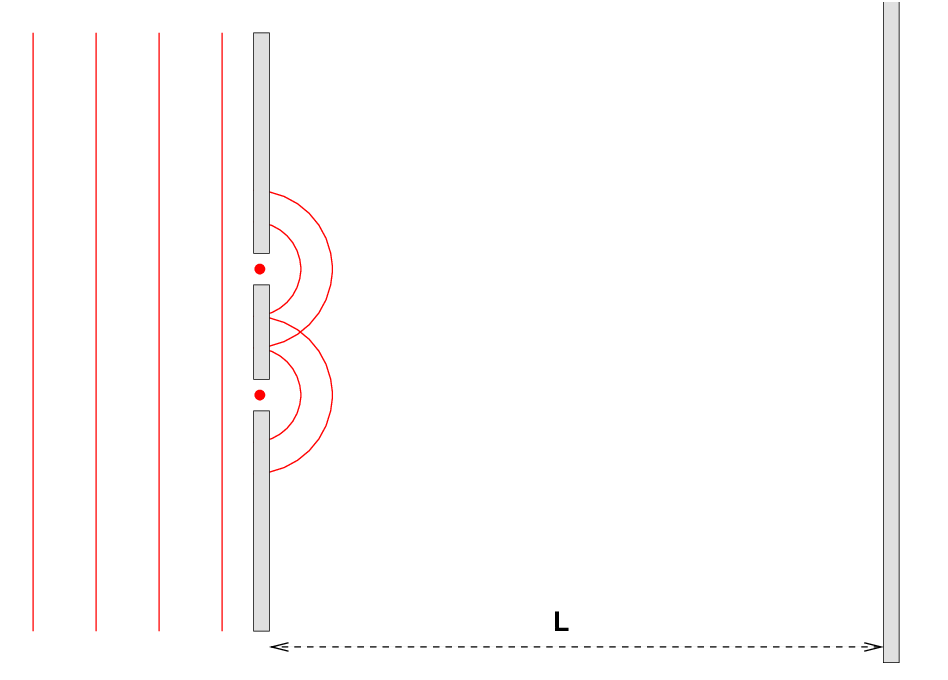
Each of these sources emits in a spherically symmetric way (well, at least hemi-spherically), so we can write the equations of waves emitted by each source as
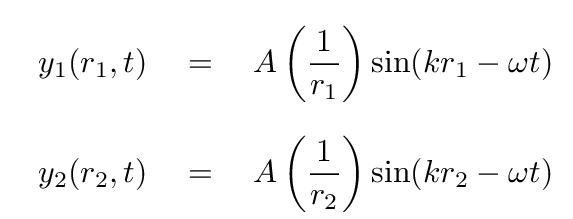
where the subscripts refer to the two slits: number 1 appears above the middle of the wall, and number 2 below.
Suppose we pick some point in the space between the walls.
Q: What is the net value of the waves at this location?
It's simply the superposition of the two waves, evaluated at this location.
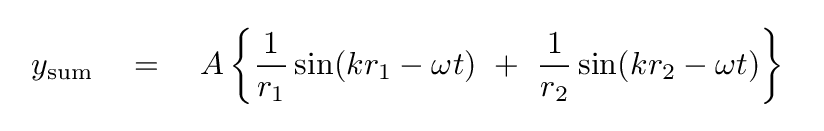
So far, so good. We've done everything exactly, and made no approximations.
However, this is as far as we can go in the general case -- without things growing really scary. Trying to understand the behavior of this sum in the near-field region, close to the two slits, requires quite a bit of mathematical sophistication. So, we're going to ignore that region, and concentrate on the simpler results in the far-field region.
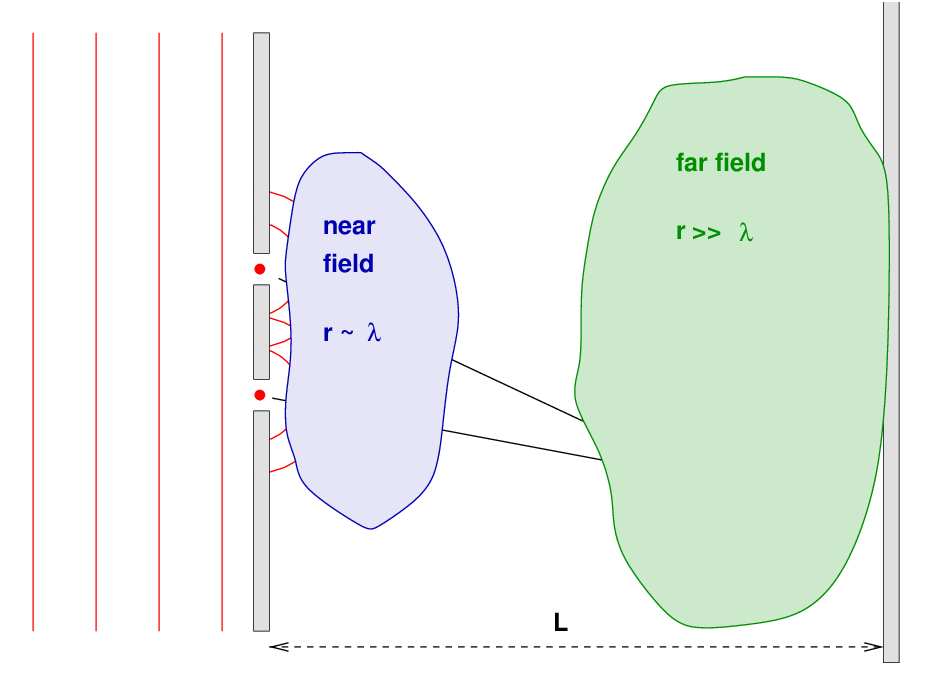
In this region, one approximation we can make safely is that the magnitude of the radial distances r1 and r2 is nearly the same, so we use an average radial distance to divide the amplitude of the sum.
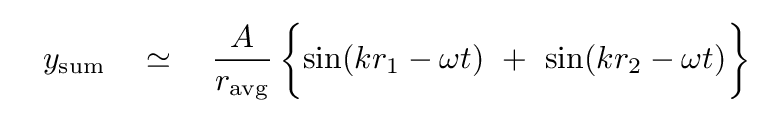
However, note that we do NOT insert this average distance in place of the distances r1 and r2 inside the sine terms. It is the SLIGHT difference between these two distances which will cause a phase offset in those sine terms; and that phase offset will cause the interesting interference effects which we will soon derive.
We can re-write this sum using one of those trignometric identities we've seen throughout this class; in particular,
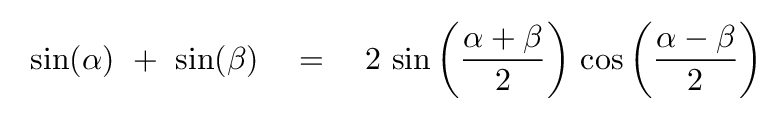
Using it, the sum of the two waves turns into
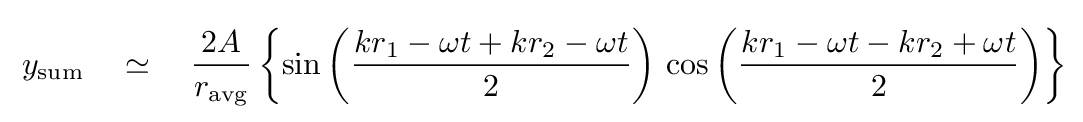
Q: Can you simplify this expression?
Indeed you can.
Now, this expression consists of the product of two terms inside the curly braces. If we consider some particular location defined by (r1, r2), then at that location
At this location, the factor of r1 + r2 inside the left-hand term simply acts as a phase offset for the sine term; the important feature of that left-hand term is that it shows the TIME-VARIATION of the sum of the two waves.
The right-hand term, on the other hand, affects the overall amplitude of the combination. It shows the SPACE-VARIATION of the sum of the two waves.
If we watch the space between the walls over some long period of time, we'll see that the sum of the waves at any location is changing with time, with the same angular frequency ω as the incident waves. Positive - zero - negative - zero - positive - zero - negative - zero, over and over again, always with the same period.
But the sum at some locations shows a big variation in amplitude over the course of this period, while the sum at other locations shows a very small variation; in fact, at some places, the sum is always zero.
How can we find those special locations where the sum is always zero? Well, zoom in on the term which controls the spatial variation:
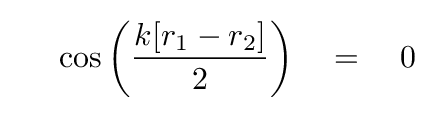
If the cosine term is equal to zero, then that means that its argument must be equal to π/2, or 3π/2, or 5π/2, or, in general,
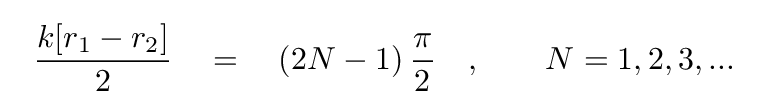
The wave number k is related to the wavelength, of course, as
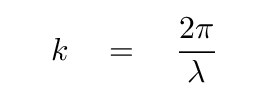
Q: Can you re-arrange these conditions to find a relationship between
the difference in path length (r1 - r2) and the wavelength λ?
You should find that the locations at which the sum of the two waves has a value of zero at all times satisfy
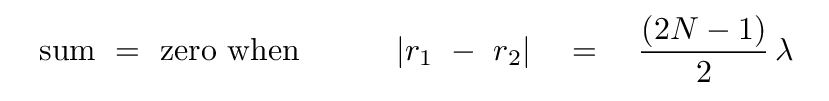
One can go through a very similar chain of reasoning to find the locations where the sum of the two waves has a maximum amplitude of variation. The starting point there is the requirement that
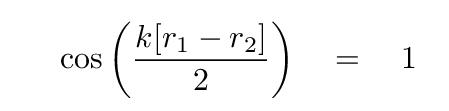
and it leads us to the condition that the sum has a maximum amplitude at locations where
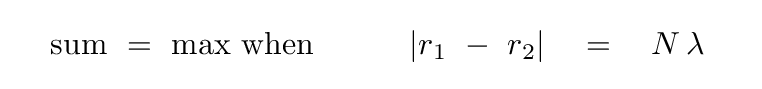
Let's look at some pictures of these interference patterns. In each picture below, the two slits are near the middle of the left-hand wall, and the light waves travel to the right.
First, we'll set d = 0.5 and λ = 0.2; in other words, d = 2.5 λ. This first map shows the AMPLITUDE of the sum of the waves from the two slits. Note the values range from -1 to +1.
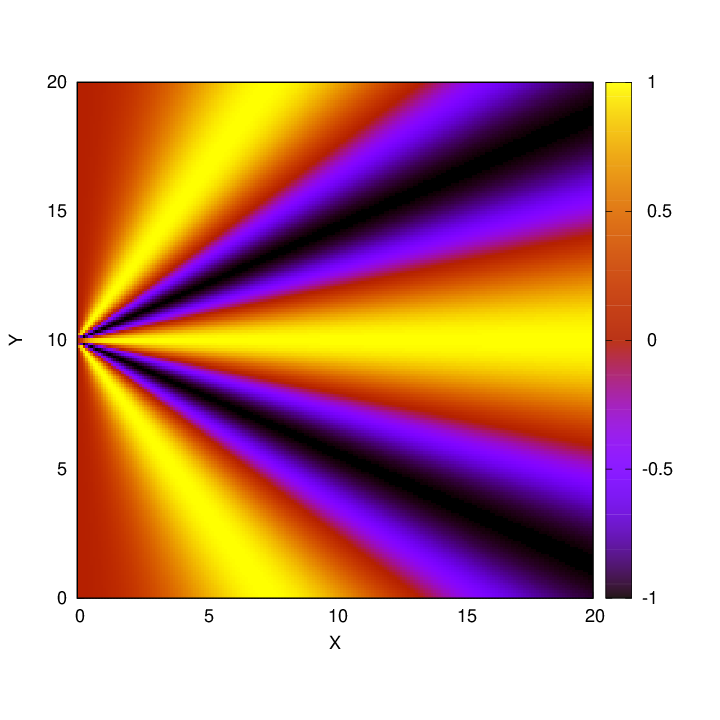
In real life, we measure the power of light waves, which depends on the SQUARE of their amplitude. In the map below, dark areas correspond to zero power -- where we would see real dark regions. Bright areas in the map below correspond to the real bright regions our eyes (or instruments) would detect. We'll show this version of the maps from this point forward, as it resembles the typical experimental results.
In the next simulation, d = 0.5 and λ = 0.1; in other words, d = 5.0 λ.
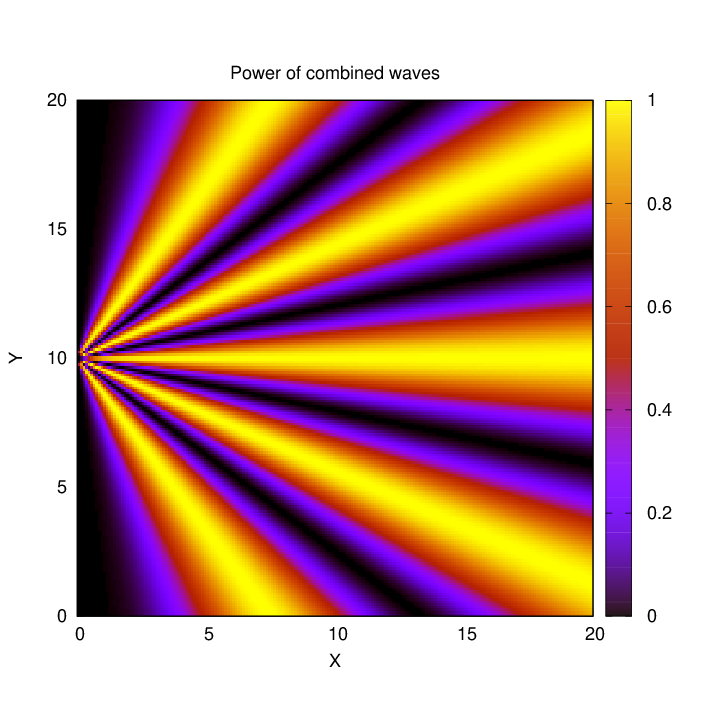
It appears that the pattern becomes more complex, showing more maxima and minima, as the spacing grows larger compared to the wavelength. So, for our final image, d = 1.5 and λ = 0.1; in other words, d = 15.0 λ.
There are other ways to figure out the two-slit interference pattern. One simple method is to look at the distance travelled by the waves from each slit when they reach the far wall.
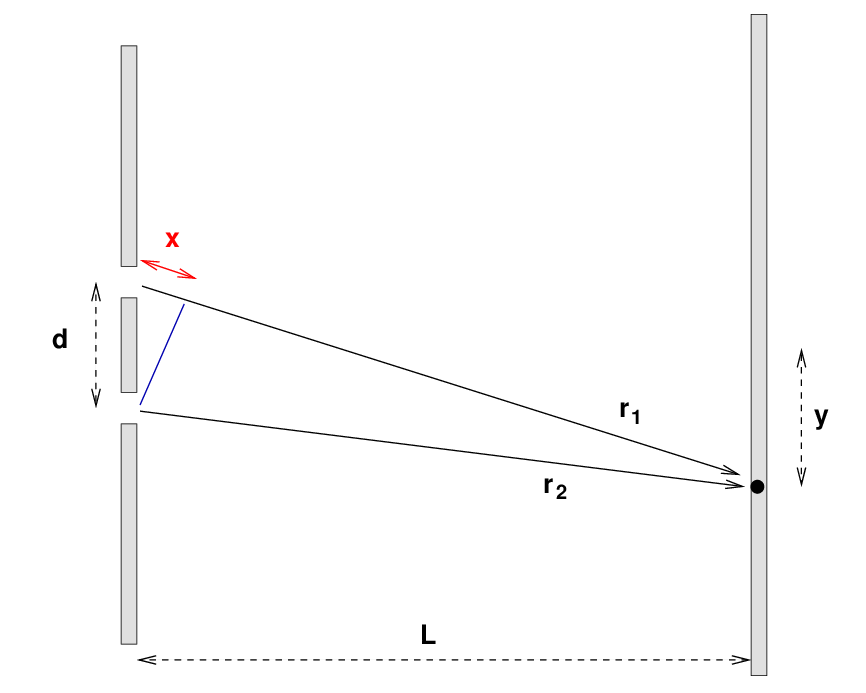
If the separation of the slits d is much smaller than the distance between the walls L, then the two radial vectors are NEARLY parallel. In that case, the extra distance x travelled by the upper wave can be approximated very well in the following manner.
First, zoom in on the region near the slits.
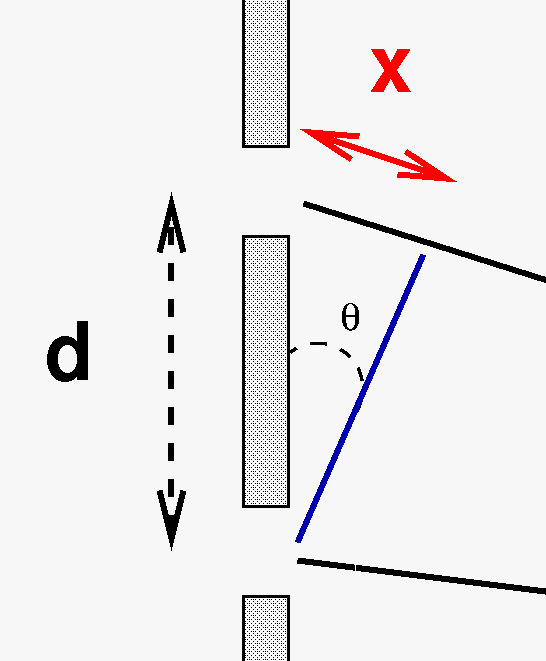
The extra distance x must be
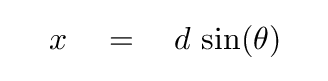
If we wish to locate a location where the sum of the two waves is zero, we require that extra distance to be an odd multiple of a half-wavelength.
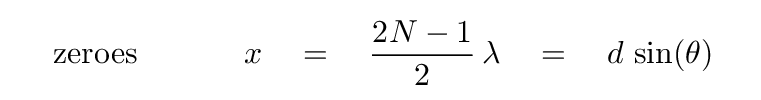
But if we now go back to look at the big picture, we can find another relationship involving sin(θ).
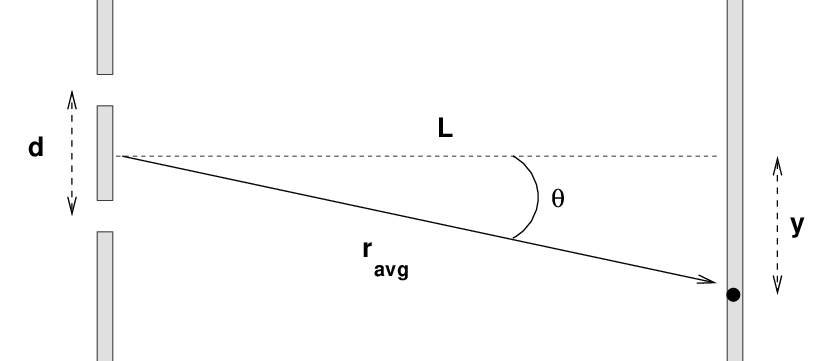
As long as the distance between the walls is much larger than the separation between the slits (which means that the angle θ is much less than 1 radian),
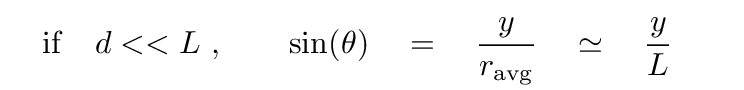
And, thus, the positions y on the far wall where the two waves interfere to create a result of zero must be given by
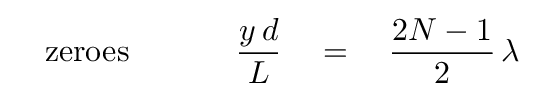
A similar equation can be used to locate the positions on the far wall where the two waves interfere to produce a maximum.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.