Figure 2 taken from Rauer, H., et al., arXiv 2406.05447 (2024)
 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Contents
Of all the future missions we'll discuss today, this should be the first to start collecting data. The launch date is currently (as of Nov, 2024) set to be "late in 2026".
PLATO is a space telescope designed, built and (soon to be) operated by the European Space Agency. The primary goal of this spacecraft is not to discover new exoplanets, but to determine more precise planetary radii (and densities) for a limited number of specifically chosen systems. The targets will be chosen so that they are sufficiently bright (say, V=11) that ground-based telescopes can measure their masses via radial-velocity observations of their host stars. Putting it all together, a set of precise radii and precise masses will allow astronomers to compute the bulk properties of certain planets very accurately.
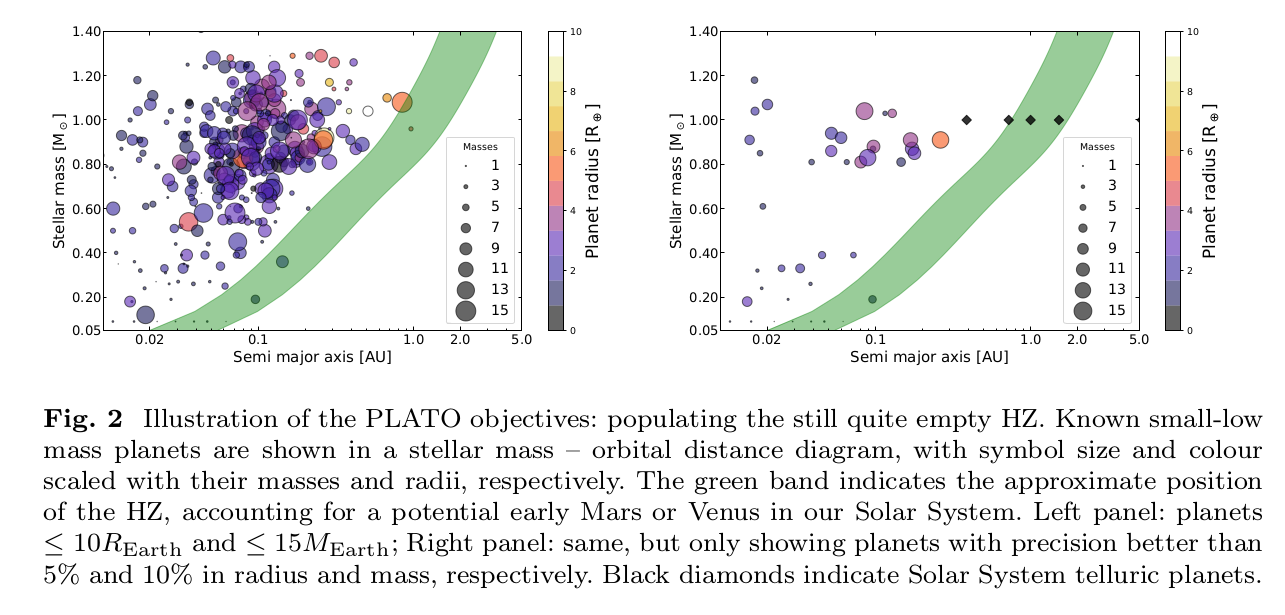
The left panel below shows a recent collection of measurements of exoplanets with relatively small masses. The green shaded region marks the Habitable Zone (HZ), the locations at which planets would have roughly Earth-like temperatures. It seems that we have discovered many low-mass planets ... until we realize that, for many of these objects, our measurements aren't very good. For example, if we throw out all the exoplanets with low-precision values of either mass or radius, leaving only the high-quality exoplanets, our sample shrinks to the set shown at right.

Figure 2 taken from
Rauer, H., et al., arXiv 2406.05447 (2024)
As an example of the sort of problems which can arise when measurements are not precise, consider this example:
We discover an exoplanet, Planet X, which has the following
measurements:
(based on transits) radius R = 9 ± 2 x 106 m
(based on radial velocity) mass M = 6.0 ± 0.5 x 1024 kg
Q: What is the range of densities consistent with these values?
Q: Is the planet water/ice or rocky?
Clearly, we need to have PRECISE values for a planet's mass and radius (especially radius) in order to determine its bulk density accurately.
How can PLATO improve the precision of exoplanet radii? Simple: it can target particular systems which are already known to be interesting, and observe their transits with a special technique. The spacecraft carries not one, but TWENTY-FOUR main cameras:
Figure 23, taken from
Rauer, H., et al., arXiv 2406.05447 (2024)

Figure 26, taken from
Rauer, H., et al., arXiv 2406.05447 (2024)
The cameras aren't all pointed in exactly the same direction. Instead, they are organized in four groups of six. Each group DOES point together, but the groups are slightly offset from each other, as shown in the diagram below. In the center of PLATO's wide field (roughly 45 degrees on a side), all 24 cameras measure the brightness of every star; but near the sides and edges, a smaller number of cameras make measurements. The result is a precision which is highest near the center of the field, and smaller near the edges.
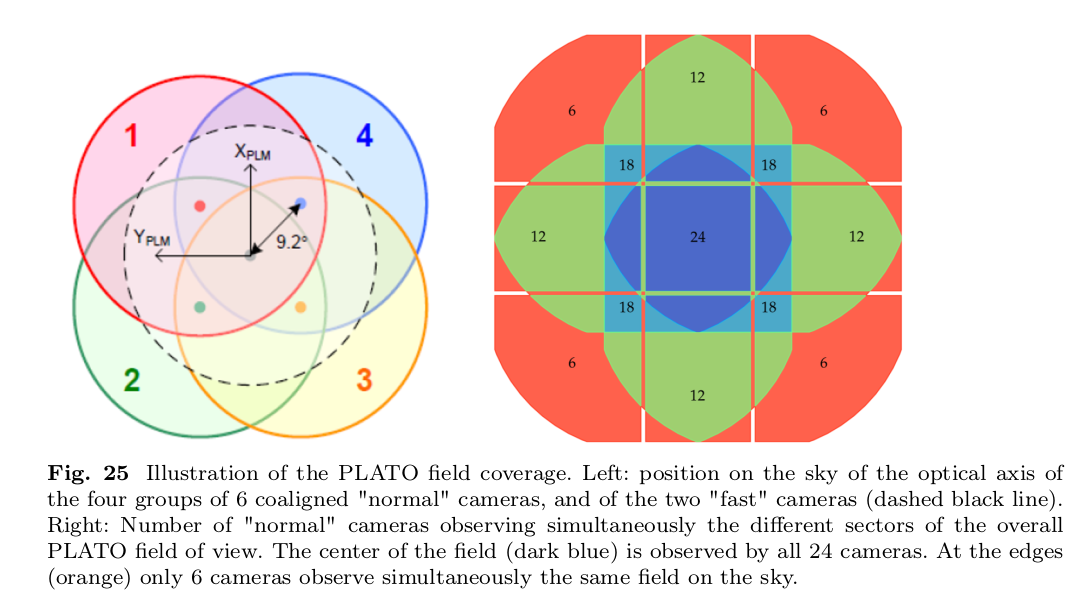
Figure 25, taken from
Rauer, H., et al., arXiv 2406.05447 (2024)
The Good News is that this observing strategy will yield measurements with uncertainties smaller than those of some other transit missions, such as TESS or CHEOPS ...
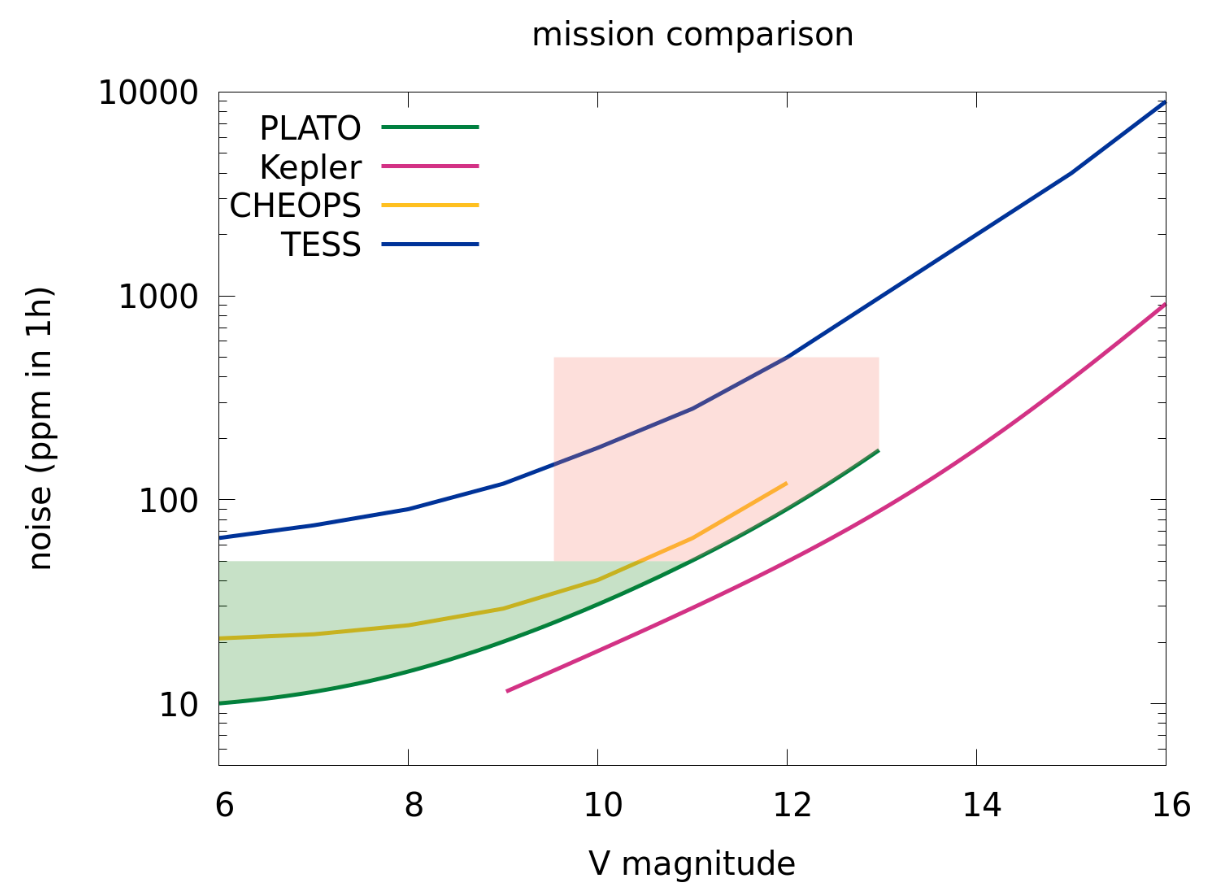
Figure 22, taken from
Rauer, H., et al., arXiv 2406.05447 (2024)
The Bad News is that the precision comes at a cost: rather than scanning many regions of the sky, PLATO is designed to stare at just two areas for long periods of time:
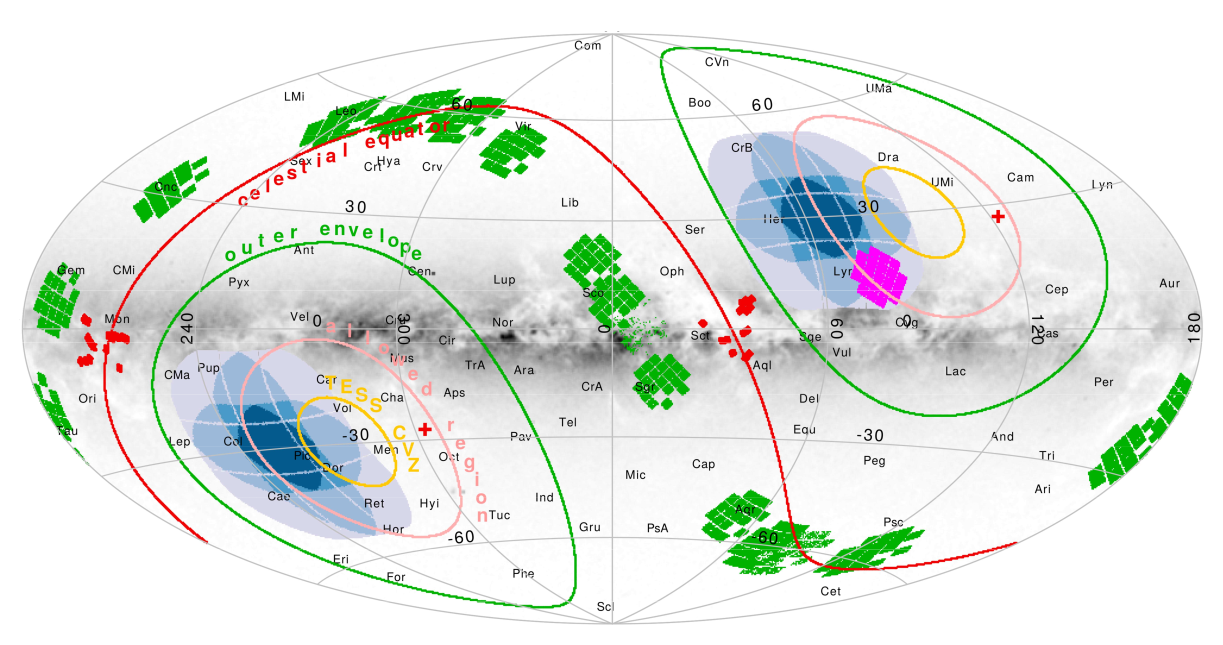
PLATO fields (blue), Kepler (pink), K2 (green), COROT (red).
TESS viewing zones are shown by the lines -- the CVZ
are at ecliptic poles.
Figure 18, taken from
Rauer, H., et al., arXiv 2406.05447 (2024)
If the team chooses these two areas carefully, they can ensure that each will contain a large number of good candidate stars: stars which are relatively close to the Sun, are bright enough to allow for high-precision photometric and radial velocity measurements, and are known to have transitting planets.
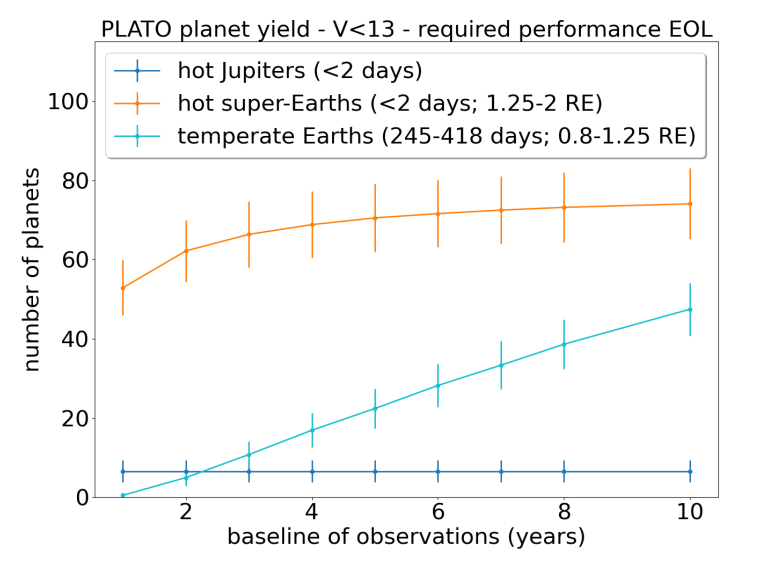
Figure 5, right panel, taken from
Rauer, H., et al., arXiv 2406.05447 (2024)
Q: Why does the number of "temperate Earths" rise steadily
over the life of the mission, while the number of "hot Super-Earths"
stops rising after a short time?
If PLATO launches in late 2026, then it might start regular observations in mid-2027, and start announcing its first results in 2028 or 2029. However, keep in mind that most of these results will be improvements to the parameters of known exoplanets. Not as exciting, perhaps, as discovering new planets, but perhaps more useful.
Over the next decade or two, astronomers will have access to several new ground-based telescopes which are larger than any in use currently, and considerably larger than any instruments likely to be put in space during our lifetimes. How will these new, big telescopes improve our ability to study exoplanets?
Let's start by comparing the three projects.
| Property | ELT | GMT | TMT |
| Operator | European Southern Observatory | Aus, Brazil, Chile, Israel, S. Korea, Taiwan, US | Canada, Japan, India (US) |
| Diameter (m) | 39 | 25 | 30 |
| Collecting area (sq.m.) | 978 | 368 | 655 |
| Location | Atacama Plateau, Chile | Atacama Plateau, Chile | Mauna Kea, Hawaii |
| Altitude (m) | 3046 | 2516 | 4050 |
| Expected start date | 2028 | early 2030s | late 2030s ?? |
In a rather surprising twist, it appears that the largest of the three may be the first one to be completed.
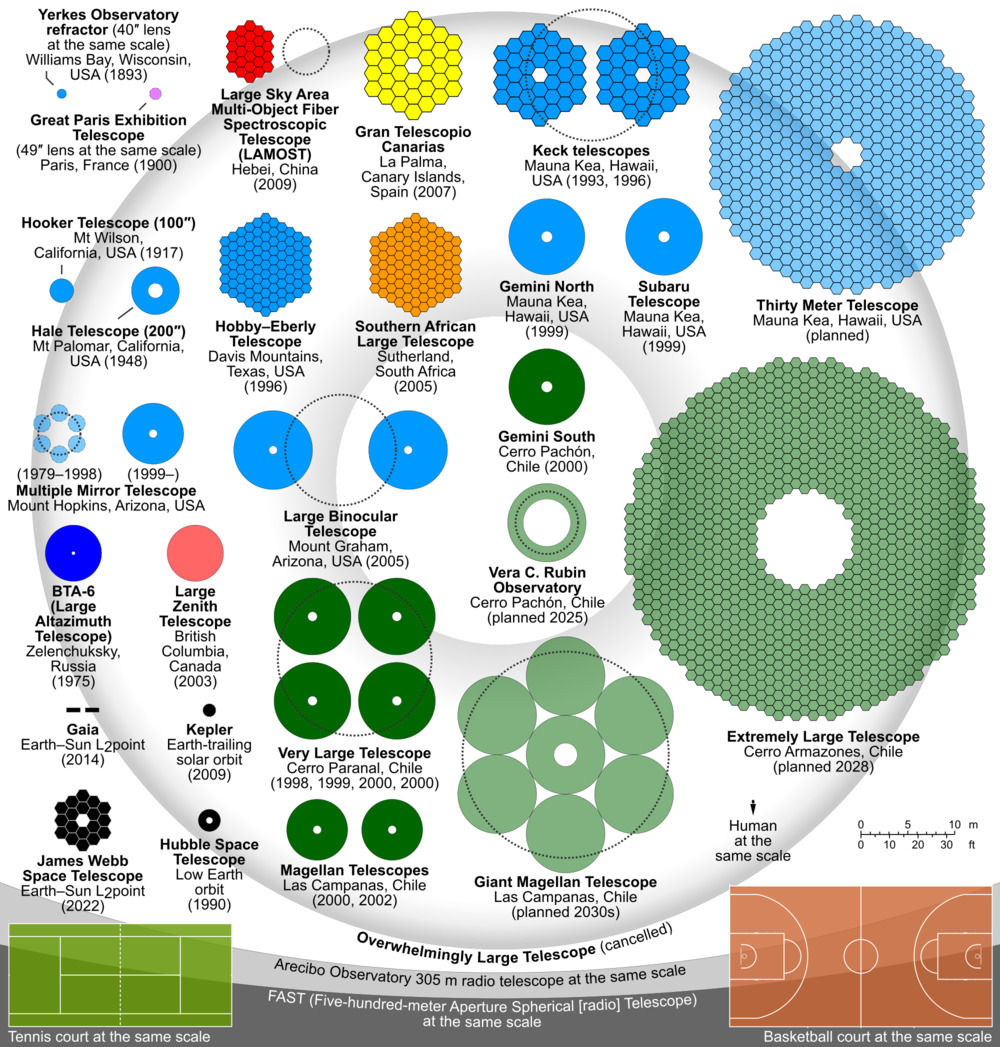
Figure courtesy of
Cmglee and Wikimedia
Now, what capabilities do these new telescopes offer?
First, let's get the Bad News out of the way: because these instrumental must look through the Earth's atmosphere, they are limited to studying only a portion of the near-infrared spectrum.
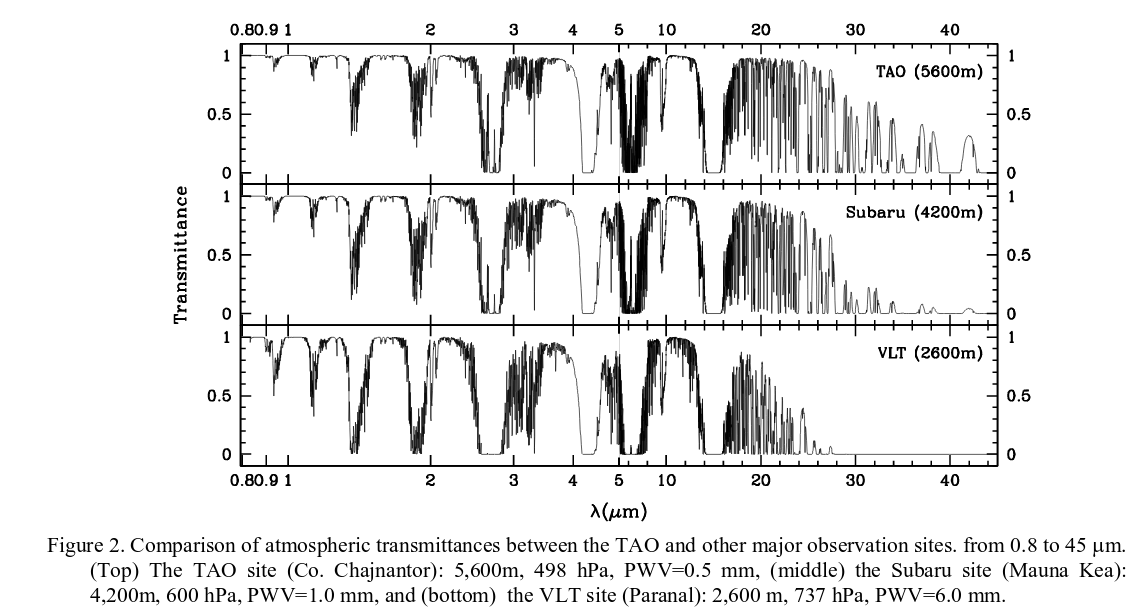
Figure 2 taken from
Yoshii et al., SPIE 2010
Large sections of the spectrum between 1 and 5 microns are wiped out by lines of (mostly) water vapor, and all wavelengths longer than about 12 or 15 microns are, for practical purposes, impossible to view. There is a window, the "N band", around 8-12 microns, which might be available. As mentioned in a previous lecture, some of the most promising spectral biosignatures lie between 7 and 10 microns, so Earth's atmosphere may make searching for those markers quite difficult.
But what about the Good News? All these telescopes are big, which opens up new possibilities in two different ways.
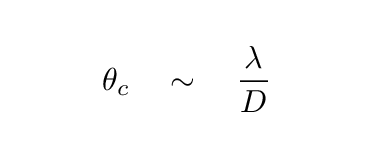
So, clearly, larger telescopes have higher spatial resolution than small ones. The largest current telescopes are roughly 10 meters in diameter, and a lot of work is done by slightly smaller instruments of diameter 5 or 6 meters. The big new generation of telescopes, with diameters of 25 to 40 meters, will lead to increases in spatial resolution by factors of 3 to 8.
(Yes, of course, use of this diffraction limit assumes that the effects of turbulence in the Earth's atmosphere can be removed; but with adaptive optics, which will be present on all these big new telescopes, infrared observations will come close to the diffraction limit).
Why is this important for exoplanet studies? For some purposes, high spatial resolution is absolutely crucial. For example, astronomers who wish to acquire direct imaging of planets around other stars face the problem of separating the light of a very faint point source from the glare of a much brighter, very close star. The picture (and movie) below show planets circling the star HR 8799.
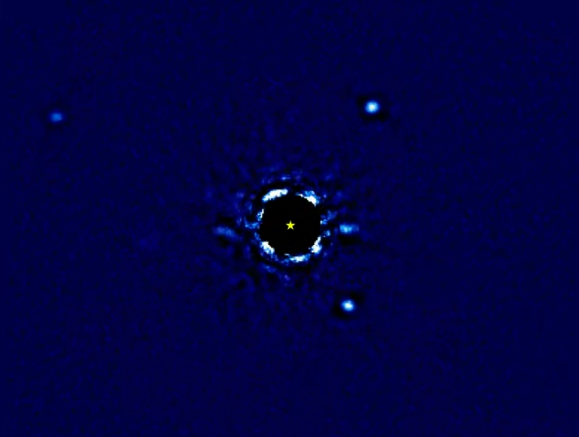
Image and movie of HR 8799 courtesy of
ESO and J. Wang and Christian Marois
This system is relatively close to the Sun, lying only 41 pc away. Despite its proximity, we can't look into the inner regions of the system to check for planets. The innermost of the objects one can see in these images, HR 8799e, has an orbital radius of about 16 AU.
A more recent image of the system was taken with the one of the VLT's 8.3-m telescopes and an adaptive optics system, as described in
The wavelength of this image is λ = 1.63 microns.

Figure 2 taken from
by Zurlo, B., et al., A&A 587, 57 (2016)
Q: What is the theoretical diffraction limit for this instrument?
Express your result in arcseconds.
Q: At what angular distance from the center of this image
could astronomers detect an inner planet?
Look at the noise levels, and express your answer
in arcseconds.
Q: If a planet were present at 1 AU from the host star,
what would its angular separation be in arcseconds?
The new generation of big telescopes will allow us to explore the regions closer to host stars; in this case, the ELT might detect objects with orbits as small as that of the Earth, or even Venus.
Another problem with studying exoplanets is that they are just plain faint: even if we can clearly separate their light from that of their host stars, there just aren't that many photons arriving every second.
To some extent, we can get around this limitation by using the plentiful light of the host star to carry the signal. The technique of transmission spectroscopy measures small changes in the spectrum of the host star as it passes through a planet's atmosphere during a transit. Smart!
Unfortunately, even this method often runs into problems due to a lack of photons. Spectrographs are not very efficient, as a general rule, due to the complex optics within, which can absorb or scatter a large fraction of the incoming photons. Even the photons that reach the detector have been split into many small groups (based on their wavelengths), and so the number in each spectral bin can be pitifully small. In homework set 3, we calculated just how many photons might be necessary to accumulate good statistics within each spectroscopic bin. In the example of that homework, the result was a minimum of about N = 1 billion photons per bin.
For JWST, with a diameter of 6.5 m, that meant that meant an exposure time of at least several minutes, even for a star as bright as mK = 7.2. Stars just a few magnitudes fainter might require exposure times of an hour to achieve the same signal-to-noise ratio.
But JWST has a collecting area of only 33 square meters. The next generation of telescopes will have ten times, or twenty times, that area, and so will be able to study exoplanets circling fainter stars. Let's see just how much of a difference this can make. We will compare JWST and ELT.
Q: What is the ratio of collecting areas?
Now, if JWST measures the spectrum of a star, and achieves a particular signal-to-noise ratio, then the ELT could reach the same signal-to-noise ratio for an identical star at a greater distance.
Q: How much farther away could the star be placed
and still yield the same S/N when observed by ELT?
The fact that the same results could be achieved for an identical star at a greater distance means that ELT could study stars in a LARGER VOLUME that JWST. If the local density of stars is roughly uniform, then sampling a larger volume means that ELT could study a larger number of stars.
Q: Assuming a uniform distribution of stars,
how many more stars could ELT observe than JWST?
Of course, there is a synergy between these two different factors: when observing faint stars very close to their hosts, a larger telescope will benefit BOTH from increased angular resolution -- which allows it to probe objects closer to the host star -- and increased collecting area -- which allows it to study smaller, fainter planets.
See
Space is a very good place to put a telescope, especially one focused on exoplanets. Not having to look through Earth's atmosphere means that space telescope can take much sharper images. If one is trying to separate the light of an exoplanet from that of its host star -- either for direct imaging, or for reflectance spectroscopy -- space telescopes are really the way to go.
Recall that most exoplanets will appear very, very close to their host stars, as seen from our vantage point. For example, an Earth-like planet with an orbit of size 1 AU around a Sun-like star will be separated from its host by an angular distance
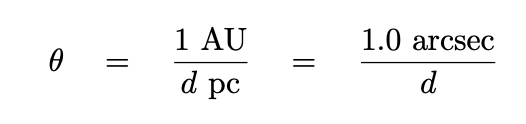
The largest telescope in space at the current time is the James Webb Space Telescope, with a diameter of about 6.5 meters. However, even when using one of its coronagraphic occulting disks, it is unable to see very faint objects if they are within a few tenths of an arcsecond of bright stars. The figure below shows the performance of the NIRCam in some early observations in flight.
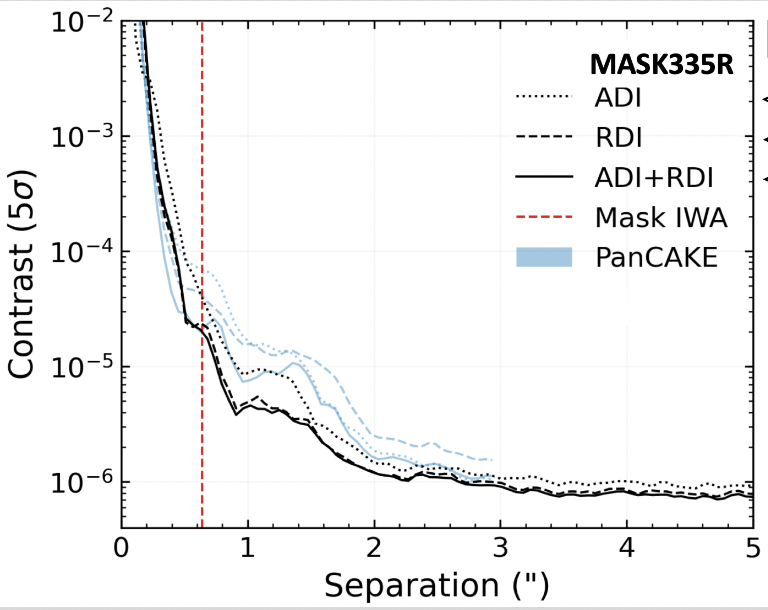
Figure taken from from
JWST NIRCam documentation
Q: The red line marks a separation of about 0.6 arcseconds from
the host star. What is the contrast ratio at that position?
Q: Is that good enough to detect an Earth-like planet in an Earth-like
orbit around a Sun-like star at 10 pc?
The contrast at 0.6 arcseconds is around 10-5. That's pretty good -- but not good enough. As we found in an earlier lecture, Earth-like planets in Earth-like orbits around Sun-like stars appear in reflected light roughly 10-10 as bright as their hosts.
If we want to see terrestrial planets in habitable zones directly, we need some way to increase the contrast of our instruments.
Could we do it by increasing the size of the telescope? Well, to some degree: larger telescopes will have a smaller diffraction limit. The "next" big space telescope will probably be the one currently known as Habitable Worlds Observatory.
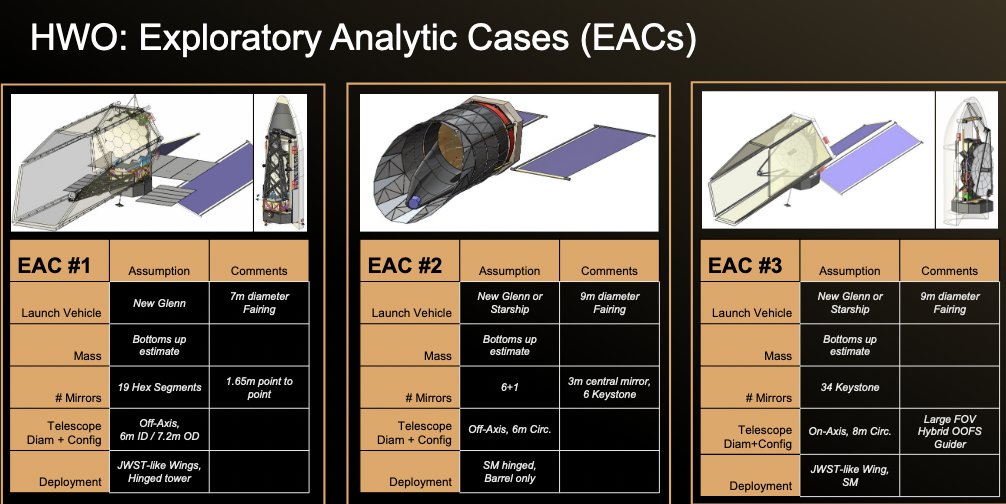
This telescope doesn't yet exist; HWO is just a name attached to a series of studies, and to an office at NASA's Goddard Space Flight Center. In the spring of 2024, NASA funded three groups, each with $17.5 million over two years, to study aspects of the development of this future space telescope.
The basic idea is that HWO will be a large space telescope which can observe across the UV, visible, and IR portions of the spectrum. Current ideas center on a telescope with diameter 6-8 meters ...
Slide taken from presentation
2024 NASA Science, Habitable Worlds Observatory
by Megan Ansdell
... so not much larger, if any, than JWST. If the telescope isn't much larger, how can it achieve much higher contrast?
Part of the answer, according to many studies, is to use a starshade to help block the light of the host star. Let's focus on that idea: just what is a starshade, and how does it work?
Start with an analogy: suppose, as you walk outside on a sunny day, your friend says, "Oh, look up in the sky over there! It's a big balloon!" You turn your head in the direction she is pointing, but the bright sun shines in your eyes, blinding you to anything else.
Q: Is there anything you can do to make the balloon
more easily visible?
Sure! Just raise your arm and put your hand in front of the Sun, blocking its light. Just make sure that your hand blocks light from the Sun, but not from the balloon.
One can do the same thing in space, putting an obstruction -- the "starshade" -- between a bright star and the telescope.
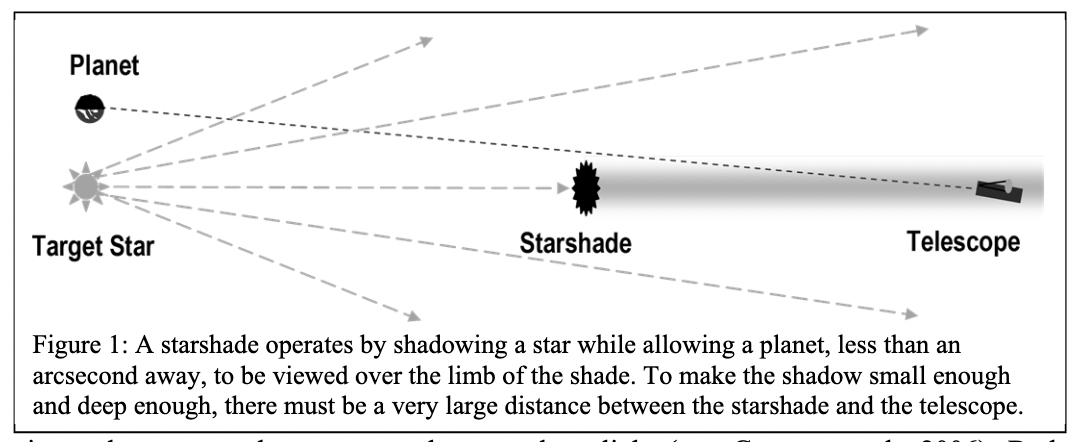
Figure 1 taken from
Cash, W., ApJ, 738, 76 (2011)

Artist's depiction of a space telescope and its starshade,
taken fron
NASA
It sounds simple, and it IS simple, in theory; but there are a few things that might make it a bit more difficult in practice.
First of all, the telescope and its shade need to be separated by a large distance -- a Very Large Distance -- in order for the shadow to be useful. How large? Let's go through some optics to find out. The main goal is find a way to make the star cast a shadow that covers the telescope, but allows the light from a very nearby planet to reach the telescope. If our starshade can block, say, 99.999% of the starlight, allowing only 10-5 of its photons to reach the telescope, then it will give the telescope's own instruments a head start to reaching the total contrast of 10-10 that is required.
In our quest to arrange things properly, we will make use of a convenient little fact of optics. Babinet's principle, named after the French physicist who worked it out, states that the diffraction pattern formed by an OPAQUE obstruction of some size and shape is the same as that created by a HOLE of the same size and shape -- except that the intensity of the light must be the opposite. Since there are lots of studies, and examples, and methods for computing the result of light passing through holes, we can use those methods to figure out what would happen if we blocked light with a starshade of the same size and shape.
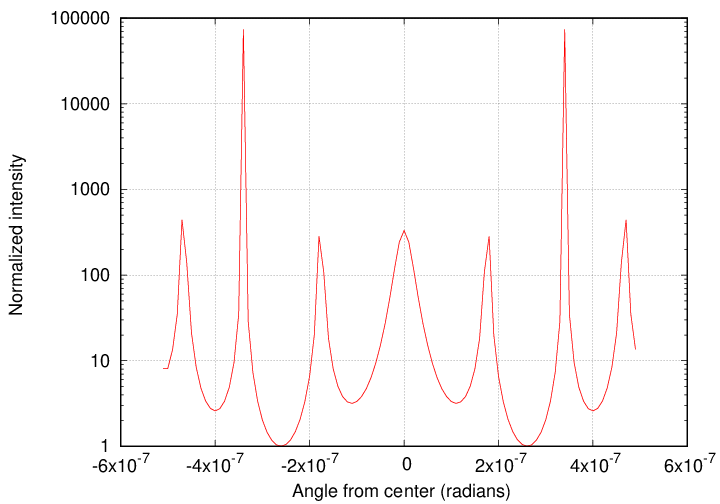
So, let's start with an easy one: what is the size and shape and intensity of a shadow, if we block light from a star with an opaque, circular disk? The answer is -- the same size and shape and intensity of a light beam which passes through a circular hole. And that's an Airy diffraction pattern.
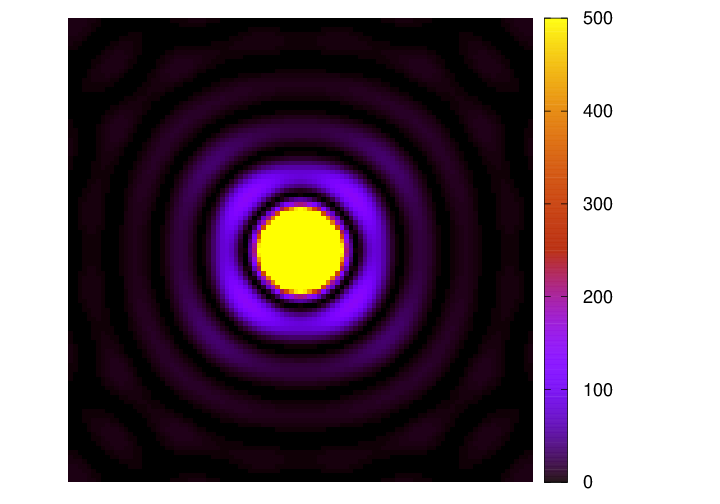
The central bright spot of this diffraction pattern has an angular radius of
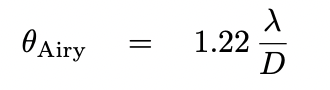
We'll imagine that the starshade has a diameter of roughly D = 10 m, and that we are observing at a wavelength of λ = 1 micron = 10-6 m. In that case, the angular distance from the bright central peak to the first dark ring is about 1.22 x 10-7 radians.
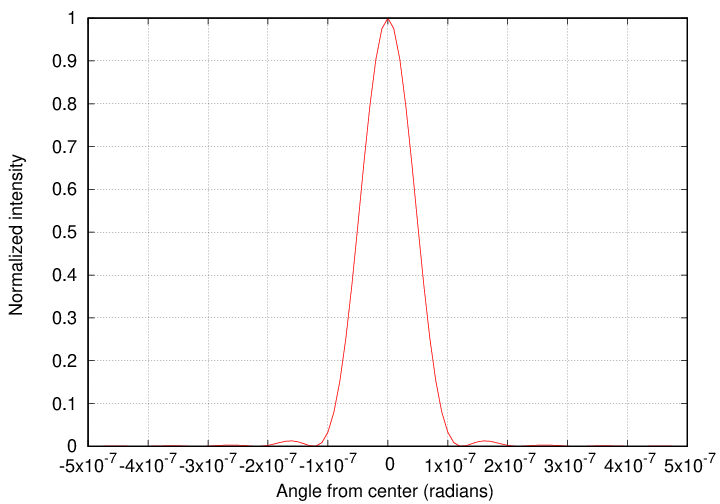
It's easier to see the contrast beween the bright and dark regions of the pattern if we use a logarithmic scale.
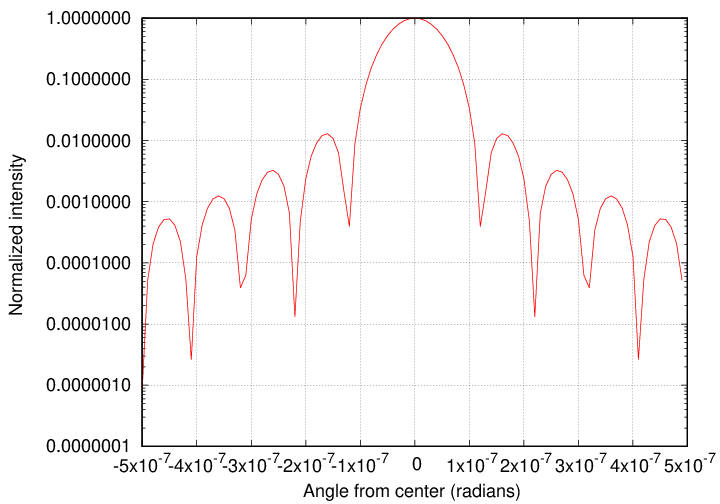
In this example,
which was computed with a low-precision algorithm,
the contrast between the intensity of light at the
center of the pattern,
and the intensity at the first mininum,
is about 10-3.
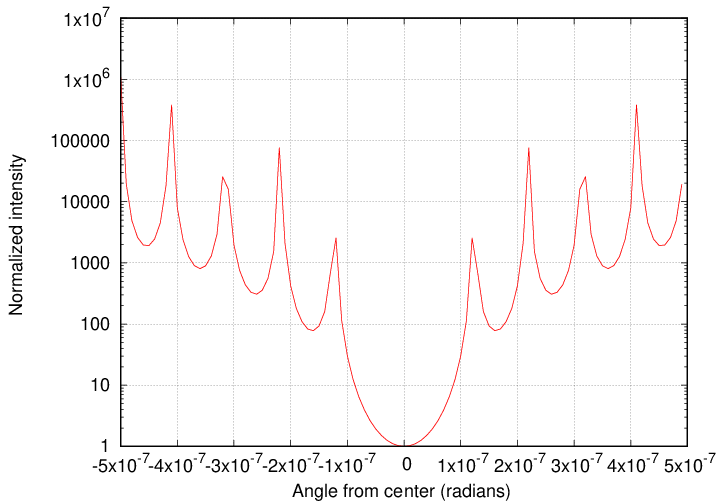
Now, if we replace the circular HOLE with a circular SHIELD,
then we'll see exactly the same sort of pattern,
except that it will be inverted:
the center of the pattern will be in shadow (dark),
and the rings around it will be bright.
The intensity of light at the center
will be only 10-3 = 0.001 = 0.1% of that intensity
at the position of the first rings.
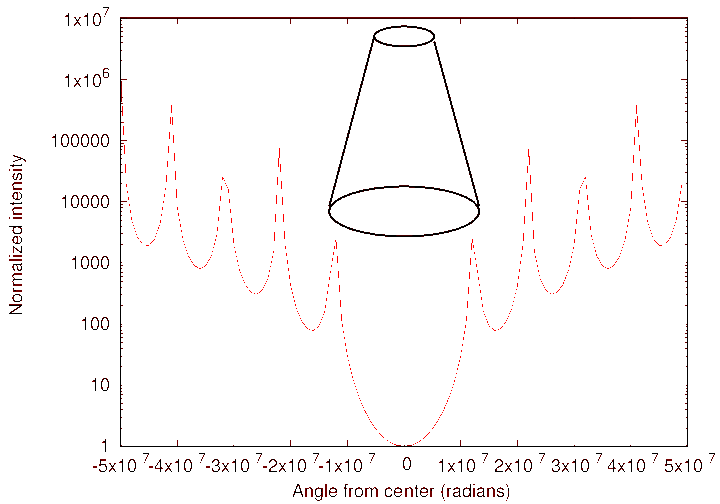
So our plan will be to place the telescope
into the center of this shadow,
where almost no light from the central
star will fall into the telescope's aperture.
Just how far from the telescope must the shield be located,
in order for the angular size of this deep central shadow
to match the physical size of the telescope's aperture?
That depends on the telescope, of course,
and to some extent on the wavelength of light
(because the diffraction pattern depends on the wavelength
of the light).
Let's put in some reasonable values and see what we get.
That's -- a really large distance.
The telescope and the shade must be placed roughly
5 Earth diameters away from each other;
or, put another way,
they must be separated by about 1/10 the distance between
the Earth and the Moon.
On top of that,
while the telescope is acquiring its images or spectra,
the relative positions of the telescope and shade
should remain stable to ... well, to some small tolerance.
How can we control so precisely two large objects separated
by such a large distance?
That is, indeed, one of the big challenges of this idea.
It seems that detecting exoplanets in this way
is as much of an engineering problem as a scientific problem.
There's another complication
which is it worth discussing.
In most of the artist's renditions of starshades,
one will see that the shade is not a simple disk,
but has jagged edges:
Why the jagged edges?
The answer is a bit complicated, and involves the detail of
the interference of many light waves as they pass
the starshield.
In particular, the behavior of the light depends on the
relative sizes of
Now, if the separation L is really, really large,
so that the following condition is met,
then this situation falls into the
Fraunhofer regime,
and the simple calculation used to compute the Airy diffraction
pattern will suffice.
In that case,
the pattern will have the properties shown above,
with a dark central shadow.
However, if one works out the math with the
numbers from our example, one will find that this condition
is NOT met for a separation L = 33,000 km;
it would have to be considerably larger to work properly.
However, since a somewhat simpler set of conditions
is met,
our system does satisfy the conditions
for
Fresnel diffraction.
It is still possible to compute the pattern of the shadow
around the starshield, but it involves somewhat more complicated
calculations;
see
the references for more details.
The crux of the problem is that, under Fresnel diffraction,
a simple circular obstruction will
NOT produce a pattern with a dark shadow
at the center.
Instead, as pointed out by
Augustin-Jean Fresnel around 1818,
light rays passing around the edges of a circular shield,
and then moving directly to the center of the pattern,
will all travel exactly the same distance;
as a result, they will meet in phase,
and create a BRIGHT spot in the center of the shadow!
This claim seemed so non-sensical -- a bright spot in the center
of a shadow?! -- that some scientists did not believe
Fresnel's calculations.
One of his colleagues,
Dominique-Francois-Jean Arago,
settled the controversy by performing
an experiment, and found that Fresnel was correct.
The central bright feature in a diffraction pattern
is sometimes called an "Arago spot" in his honor.
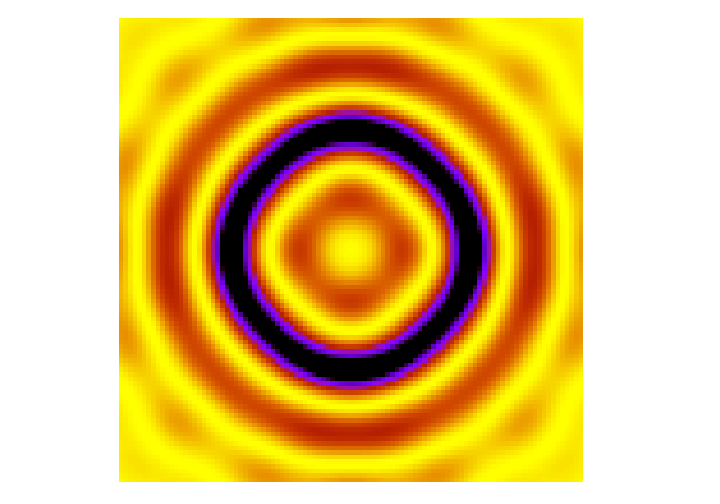
And so, if one were to build a simple circular starshield
of diameter D = 10 m
place it L = 33,000 km
from a telescope,
and observe at a wavelength of λ = 1 micron,
one would find an unwelcome visitor in the middle
of the shadow.
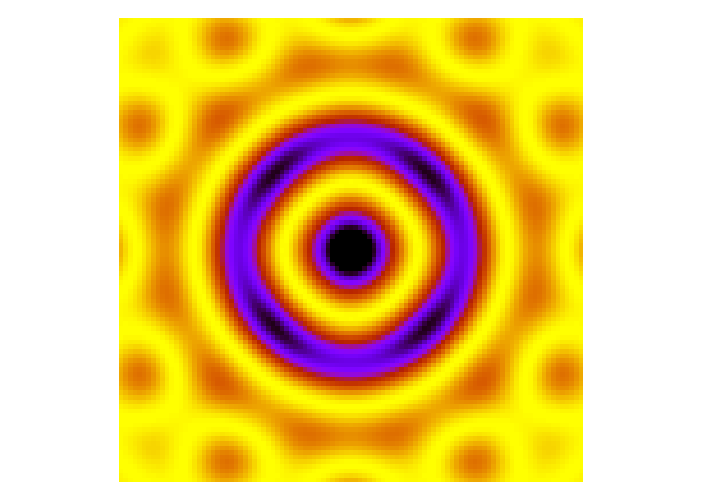
(The picture below shows yellow = bright, black = dark)
We can get rid of the bright Arago spot by apodizing
the edge of the starshield:
gradually decreasing its opacity with radius towards its outer edge.
If we choose just the right manner to decrease the opacity,
then light rays from the very edge of the shield will
interfere destructively with some other light rays which
pass though the outer sections of the partially-transparent
shield,
leading to a much fainter spot in the center.
From a practical point of view,
it's difficult to manufacture a material with
a precisely controlled opacity over a large distance
(3 or 5 or 8 meters).
Clever astronomers realized that one could gain
most of the benefits of apodization by gradually
decreasing the amount of blocking material
near the edges using
PETALS:
Finding just the right number and shape and size
of the petals is a problem which will take a lot of work.
I did a very simple simulation using
just 12 petals and spent 5 minutes fiddling with
the parameters.
But even this simple version does remove most
of the light from the central spot of the shadow.
Suppose the diameter of the starshade is D = 10 m,
and the wavelength of light is 1 micron = 10-6 m.
Then the angular radius of the first minimum of the
pattern is θ = 1.2 x 10-7 radians.
Q: If the telescope has a diameter of d = 8 m
at what distance L must we place the starshade
so that the telescope just fits into the first minimum
of the pattern?



Artwork courtesy of (left to right)
NASA,
NASA/JPL-Caltech,
National Geographic
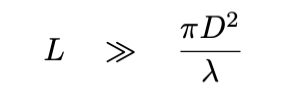

Photograph of Arago spot experiment from
Aleksandr Berdnikov and Wikimedia

Artist's depiction of a starshade with petals
taken fron
NASA

For more information
 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.