Four methods of predicting a baseball team's final record

Michael Richmond
July 8, 2007

Can we predict the final record of a team based upon its performance at some intermediate point in the season? Sure -- but we might not be right. In this brief document, I compare four methods for making predictions. I use historical records from the American League, 1961 - 2007, excluding the strike-shortened years of 1972, 1981, 1994, 1995.

For background information and a detailed description of some of the models, see

• Predicting the final record of a baseball team during the season
• Predicting the number of runs a team will score or allow
• Sosh Wiki explanation of Pythagorean theorem for baseball

The four methods I'll consider are

naive extrapolation

Take the current winning percentage and multiply by 162 games. Example: after 50 games into the season, the 2006 Boston Red Sox had a record of 30 wins and 20 losses, for a winning percentage of 0.600. This method predicts

             naive extrapolation    162 * (0.600)  =  97  wins
         

linear model to current winning percentage

Use historical records to derive a linear relationship between current winning percentage and final winning percentage; apply that linear model. Example: as shown in this report, after 50 games, the best-fit model is

 
  final winning percentage  =  0.207  +  0.599 * (current win percentage)

                            =  0.207  +  0.599 * (0.600)

                            =  0.566

         model to winning perc      162 * (0.566)  =  92  wins
          
       

linear model to current Pythagorean percentage

Use historical records to derive a linear relationship between current Pythagorean percentage and final Pythagorean percentage; apply that linear model. After 50 games, the 2006 Red Sox had scored 276 runs and allowed 244 runs, for a Pythogorean percentage of 0.561. Using historical team records, a model connecting the current Pythagorean percentage to final Pythagorean percentage is

 
  final Pythag percentage   =  0.187  +  0.624 * (current Pyth percentage)

                            =  0.187  +  0.624 * (0.561)

                            =  0.537

         model to Pythag perc      162 * (0.537)  =  87  wins
          
       

linear model to runs, then apply Pythagorean theorem

Use historical records to derive linear relationships between current runs scored and final runs scored, and between current runs allowed and final runs allowed; in other words, predict the final runs scored and allowed. Then apply the Pythagorean theorem with those predictions. After 50 games, the 2006 Red Sox had scored 276 runs and allowed 244 runs; as shown in this report, we can first predict that the team would score 846 runs and allow 769 runs. Then we can compute a final winning percentage:

 
  final winning percentage  =  (846*846) /  (846*846 + 769*769) 

                            =  0.548

    model to runs, apply Pyth      162 * (0.548)  =  89  wins
          
       

What I did to compare these methods was

• look at the records and runs scored and allowed for each team during the study period, after 1 game, 2 games, 3 games, ..., 162 games into each season
• use each method to predict the number of wins after 1 game, 2 games, 3 games, ..., 162 games
• compare each prediction with the teams actual number of wins
• compute the error in each prediction using all teams and all seasons, after 1 game, 2 games, 3 games, ..., 162 games
• calculate mean and stdev of these errors

The results can be shown in a single graph. On the x-axis is the number of games played into the season, and on the y-axis is the standard deviation of the difference between predicted and actual number of wins at the end of the season. The smaller the standard deviation, the better the prediction.

Take just a quick glance at this figure -- the one you'll want to study closely is the next one. All this does is show how poorly "naive extrapolation" does at early times.

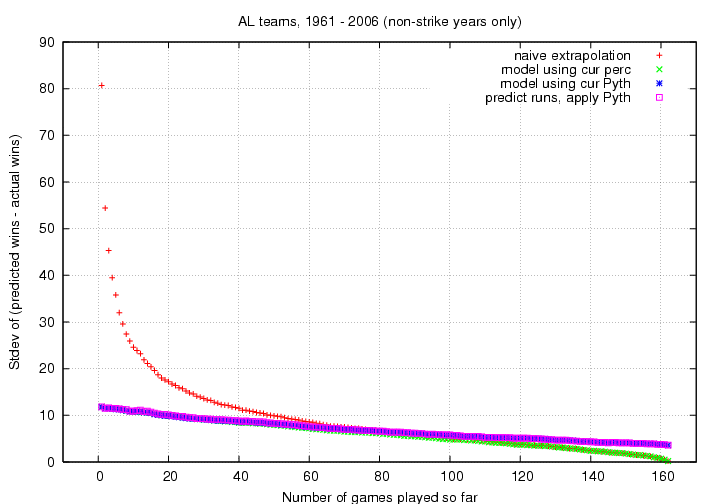
Pay attention to the graph below, which just zooms in on the interesting region.

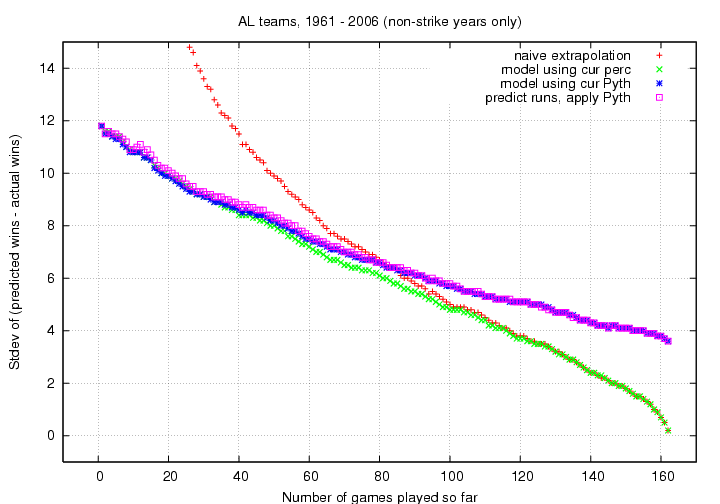
The results are easy to summarize, to a fair degree:

• Before the All-Star Break, naive extrapolation of a team's current record is worse than more sophisticated methods
• after the All-Star Break, naive extrapolation is about as good as more sophisticated methods
• a model which starts with a team's current record is as good as or better a model with starts with runs scored or allowed
• simply Pythagorean methods yield a standard deviation of around 4 wins, even at the very end of a season

Copyright © Michael Richmond. This work is licensed under a Creative Commons License.