 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Spoiler alert: today's lecture discusses methods for finding planets around other stars which have turned out to be wildly successful.
Remember the Doppler shift?
If an object moves towards or away from an observer, the electromagnetic waves it emits will be shifted to shorter or longer wavelengths, respectively. Sometimes we call those changes in wavelength blueshift (if the object is coming toward us) or redshift (if the object is moving away).

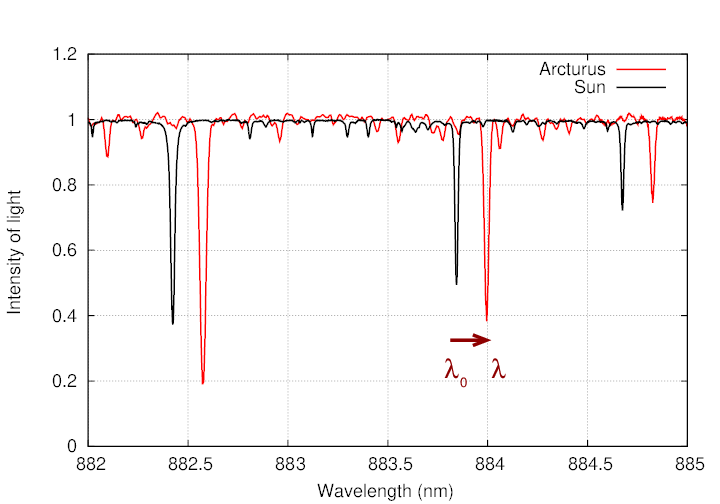
Consider the star Arcturus, which is not unlike the Sun. If we look at the spectrum of light from the Sun, and the spectrum of light from Arcturus, we see the same pattern of absorption lines; but the lines in the spectrum of Arcturus are shifted to slightly longer wavelengths.
Q: What is the shift in wavelength (λ - λ0) ? Q: Is Arcturus moving toward us, or away from us? Q: What is the speed of Arcturus toward/away from us?
Perhaps this equation might help:

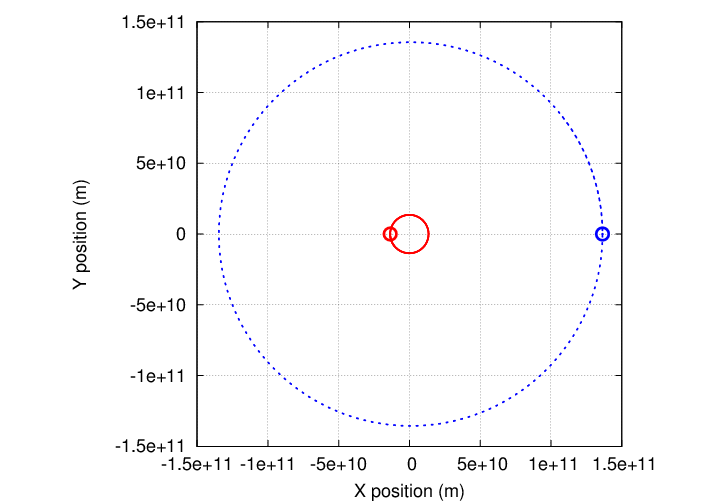
How could we use this Doppler effect to find planets around other stars? Well, consider a planet which orbits around a distant star. As the planet moves in a big circle around the center of mass of the system, the star will move in a little circle around the center of mass.
If we look at such a planet-plus-star system from above, we would see something like this:
But if we look at the system from the side, so it appears edge-on, we would see something like this (click on the image to activate an applet)
As the star moves in its little orbit around the center of mass, the wavelengths of light that it emits will appear to shift longer and shorter, longer and shorter. Even if we can't see the planet directly, we might be able to detect this periodic change in the star's spectrum.
Let's see what it might look like in action. Suppose that Arcturus was orbited by a planet, and that planet's gravitational pull was so strong that it made Arcturus move around its center of mass with a speed of 10,000 m/s. If we measured the spectrum of Arcturus night after night, we might see changes like this: (refresh this webpage, if necessary, to restart the animation below)
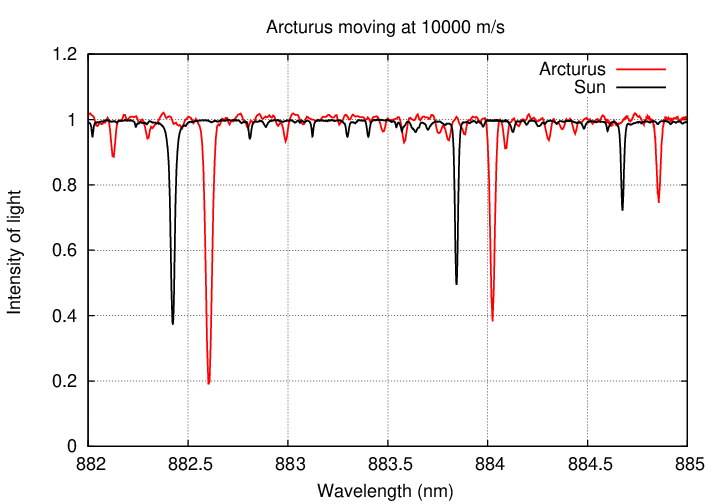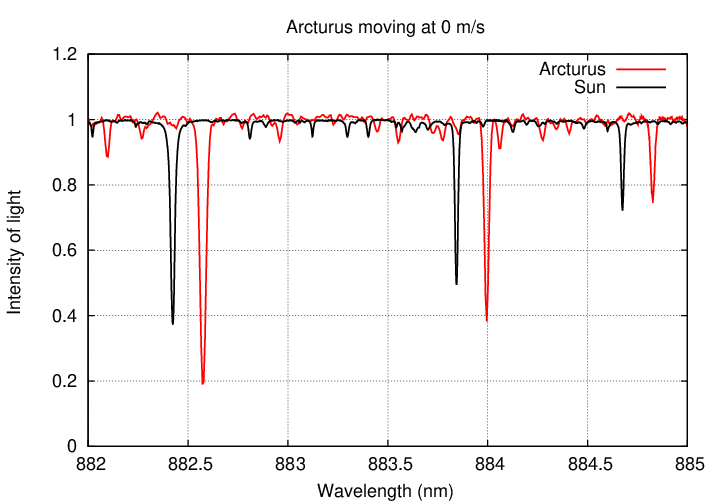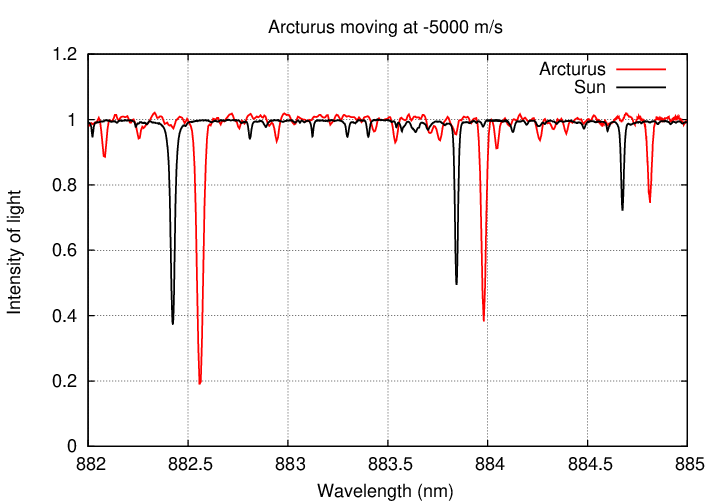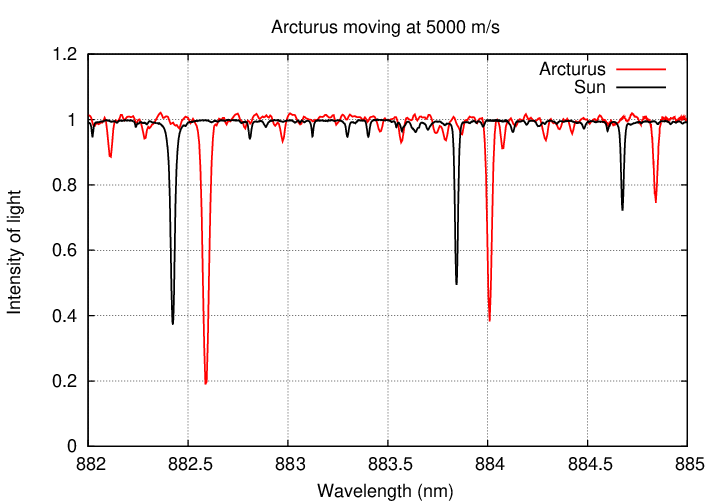
Q: Would it be easy for astronomers to detect motions of 10,000 m/s?
Yes, of course.
But suppose that the planet's gravitational pull was weaker, and Arcturus moved more slowly. What if it circled the center of mass with a speed of only 1,000 m/s? (refresh this webpage, if necessary, to restart the animation below)
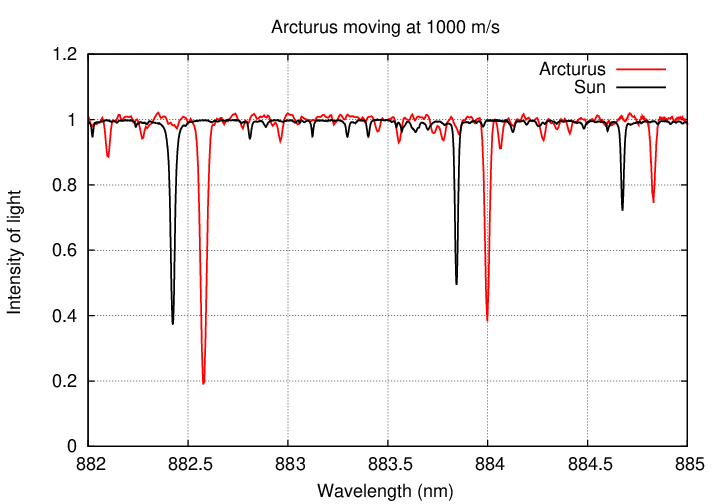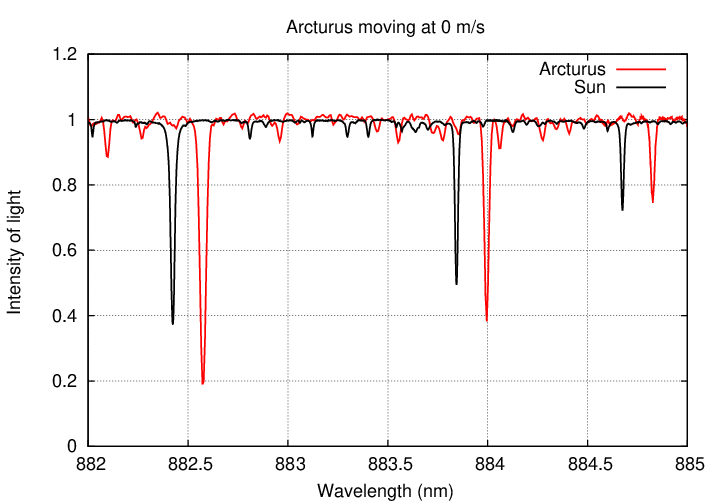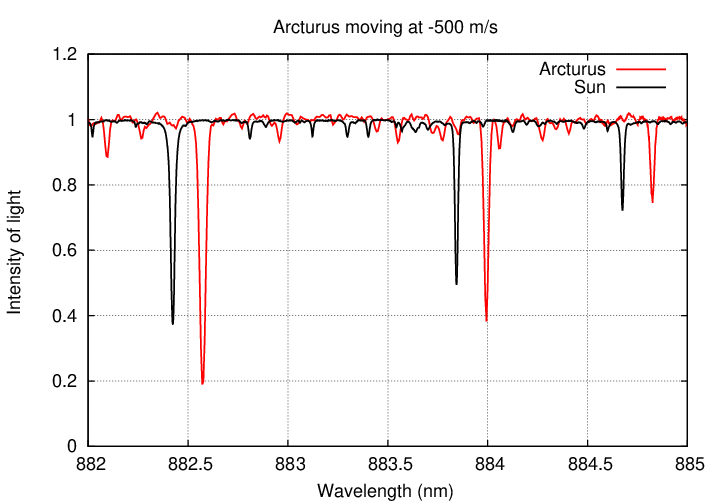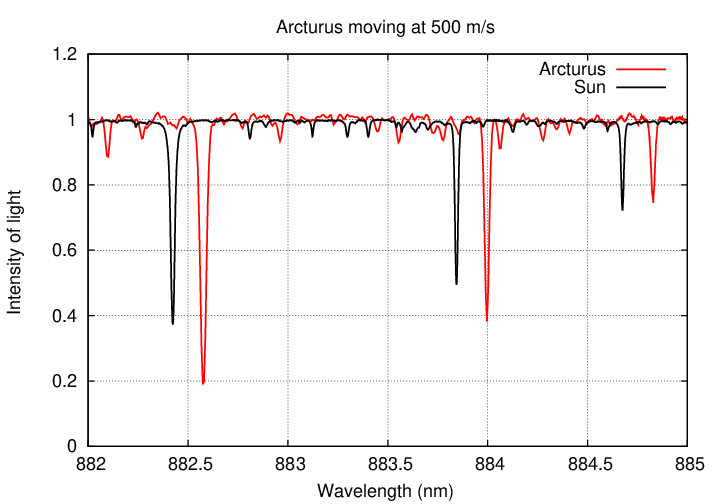
Q: Would it be easy for astronomers to detect motions of 1,000 m/s?
Well, not easy ... but possible. If we just zoom in a bit in our graph, small changes become easier to see. (refresh this webpage, if necessary, to restart the animation below)

Well, what if the gravitational pull of the planet were smaller still? Suppose that the star only moved at 100 m/s? (refresh this webpage, if necessary, to restart the animation below)

Okay, so now you have some feeling for how easy or hard it might be to detect these radial velocity variations. Let's see how big they might be in practice.
Watch a video explaining the following calculations
![]()
Jupiter orbits its center-of-mass with the Sun once every 11.9 years, in an orbit with a size of about 5.2 AU. The Sun must orbit the center-of-mass with the same period, but how big is its orbit? The answer can be found in the figure below.

mass of planet
size of star's orbit = (size of planet's orbit) * ----------------
mass of star
In the case of Jupiter and the Sun, we have
mass of Jupiter = 1,898 x 1024 kg
mass of Sun = 1,988,500 x 1024 kg
Jupiter to CoM = 5.2 AU = 7.8 x 1011 m
Sun to CoM =
Right. Because the mass of Jupiter is bout 1/1000 of the mass of the Sun, the distance from the Sun to the Center-of-Mass is about 1/1000 of the distance from Jupiter to the Center-of-Mass.
So, now that we know the size of the little circle around which the Sun moves, can we figure out the speed of the Sun's motion?
Q: What is the speed of the Sun around its Center-of-Mass
with Jupiter?
That's ... a pretty slow motion. It means that detecting the Sun's motion due to Jupiter would be pretty difficult.
Does this really work in practice? The answer is "yes!" Back in 1995, two astronomers working in Europe, using a relatively small telescope (just 1.9 meters in diameter), measured the following motions in the star 51 Peg.
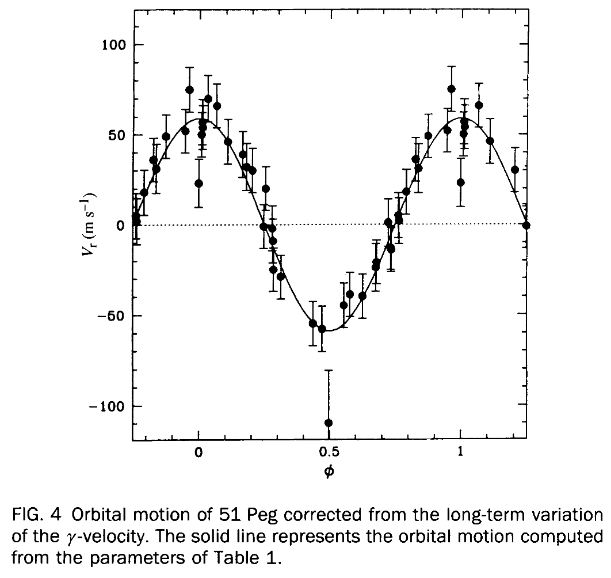
Figure 4 taken from
Mayor and Queloz, Nature 378, 355 (1995)
The speed of the star in this case was about 60 meters per second -- fast enough that it produced shifts in wavelength which were not too difficult to detect. One of the reasons that the speed is so large is that this planet is massive: about 0.47 Jupiter masses.
The other reason that the star is moving so fast is that the orbital period is small. Really small. Teeny-tiny. The planet takes only 4.2 days to complete one revolution; and so the star has only 4.2 days to make its own orbit around the Center-of-Mass.
Four point two days! you might say. That's impossible. Why, even Mercury, the planet closest to the Sun, takes 88 days to complete one orbit.
True. But this planet was unlike any in our Solar System. Its orbit really was tiny -- only 0.052 AU in size. So tiny that the planet must be scorched.

Q: Assuming the star 51 Peg is like our Sun, what would
the temperature of the planet be?
Like I said, hot!
In the years since 1995, astronomers have discovered many other planets by this same "radial velocity" technique. It turns out that many of these planets are like 51 Peg b: as massive as the gas giants in our own Solar System, but orbiting much, much closer to their host stars. Astronomers have given planets of this type a special name: "hot Jupiters."
The radial velocity technique has been very successful. The count is (as of August 2, 2020) up to ...
Q: If you look at the NASA exoplanet archive site,
and ask for planets with Discovery Method equal to "Radial Velocity",
how many are there?
Astronomers have been improving their instruments so that they can detect smaller and smaller variations in wavelength, and so they can detect planets with smaller and smaller mass. Could they detect an Earth-like planet orbiting around a Sun-like star?
Q: The Earth orbits the Sun at a distance of 1 AU,
with a period 1 year = 3.15 x 107 seconds.
mass of Earth = 6 x 1024 kg
mass of Sun = 1,988,500 x 1024 kg
Earth to CoM = 1.0 AU = 1.5 x 1011 m
Sun to CoM =
How fast does the Sun move around the C-o-M with the Earth?
Astronomers can't detect such tiny motions .. yet. But they are working on it.
Relatively recently, Nov 14, 2018, astronomers announced that they had found a planet circling Barnard's Star. Yes, that same Barnard's Star that turned out NOT to have Jupiter-like planets orbiting at 2 or 4 AU; the astrometric measurements were too noisy, and the apparent signals were not real.
But the radial velocity technique may have found quite a different planet: one with about 3 times the Earth's mass, orbiting with a period of about 233 days. I write "may" because the data seem a bit noisy to me. What do you think?

Figure 3 taken from
Ribas et al., Nature, 563, 365 (2018)
The radial velocity method has revealed hundreds of planets circling other stars ... but it is not the most prolific technique. A different method has helped astronomers to find THOUSANDS of planets. What is this most effective means of finding extrasolar planets? We call it the transit method.
The basic idea is pretty simple: if a planet happens to move in front of its star, it will block a small amount of the light. All we have to do is to stare at a star for a long time, measuring its brightness VERY precisely, and wait to see a dip. And then another one, and then another one, all at regular intervals.
Sounds pretty simple, and it is pretty simple. Of course, it is necessary to measure brightness VERY precisely, because even a big planet will block only a small fraction of its host star's disk.

Sun radius 696 x 103 km
Jup radius 71.5 x 103 km
Earth radius 5.97 x 103 km
Q: What fraction of the Sun's light will Jupiter block?
What fraction of the Sun's light will the Earth block?
As long as one is careful, and patient, one can detect the dips in brightness caused by the big planets -- the size of the gas giants in our own Solar System. And one doesn't need a giant telescope or really expensive instrument to make these measurements, either.
The very first transit ever detected was measured by the STARE telescope, just four inches in diameter!

Image courtesy of
the STARE project
Watch a video explaining how to compute the size of a planet based on the dip in its star's light
![]()
On the nights of September 9 and 16, 1999, this little telescope noticed that the star HD 209458 decreased in brightness for just a few hours.
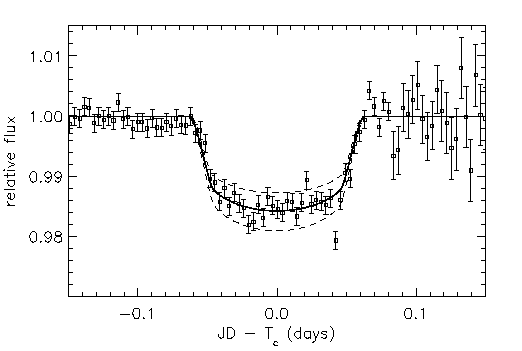
Image courtesy of
the STARE project
Q: How deep is that dip in brightness? In other words, what fraction
of the star's disk was covered?
Q: If that star is like our Sun, how large is the planet?
A planet roughly 1/10 the radius of its star? Sounds like a gas giant ...
This transit technique doesn't require big telescopes or fancy equipment, and so even astronomers with small telescopes can do it. Yes, even the little 12-inch telescope at the RIT Observatory has been able to detect a planet passing in front of its star.
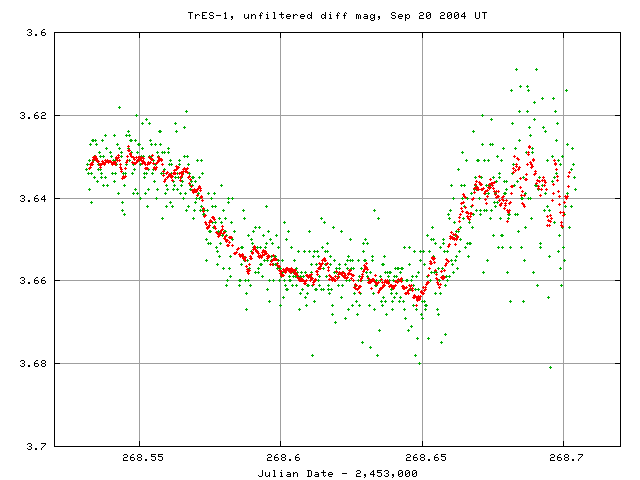
Image courtesy of
RIT Observatory
But if you want to find the SMALLEST planets via the transit technique, you do need to collect a lot of light, and use high-quality detectors. It also helps if you move up above the atmosphere to avoid the variations caused by clouds and dust in the air. NASA's Kepler mission placed a telescope of diameter 0.95 meters into space, and pointed it at one region of the sky, near the Milky Way, for three years.

Image courtesy of
NASA/JPL
The telescope focused its light onto a camera in the middle of the tube ...

Image courtesy of
NASA Ames

Image courtesy of
NASA Ames and Ball Aerospace
Over the course of its three-year primary mission, Kepler detected over one thousand planets circling other stars.
How precise are the measurements made by Kepler? Take a look at the scatter in the simulated light curve below. Note that the label on the y-axis states that the units are parts per million.

Image courtesy of
Kepler Science Center
Q: Would a light curve of this precision be good enough to detect
an Earth-like planet orbiting a Sun-like star?
There's no doubt that Kepler provided a huge advance in our understanding of planets around other stars. Even though the mission ended back in 2018, it remains the most prolific finder of exoplanets yet created.
Q: If you look at the NASA exoplanet archive site,
and ask for planets with "Host Name" equal to "Kepler",
how many are there?
Right now, a different NASA spacecraft is continuing to search for extrasolar planets. TESS (Transiting Exoplanet Survey Satellite) cannot make measurements with the same very high precision as Kepler did, but, unlike Kepler, it will eventually scan the entire sky for new targets.
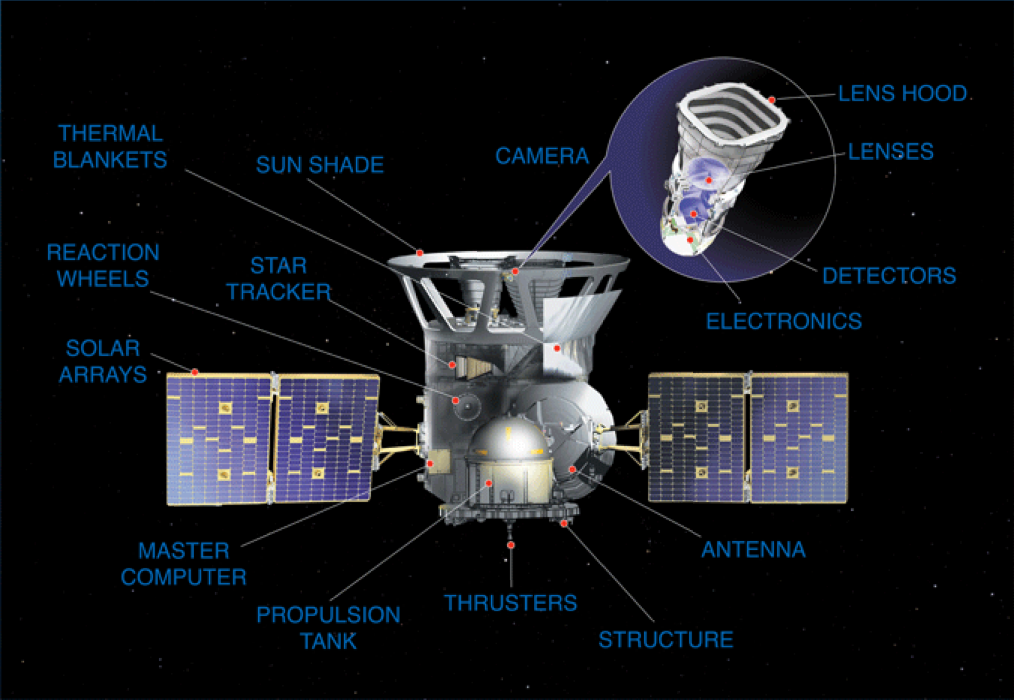
Image courtesy of
MIT and NASA GSFC
TESS spends about one month looking at one region of the sky with its four cameras, and then moves to look at a different region.

Image courtesy of
MIT's website for TESS
On July 4, 2020, TESS will finish its complete scan for planets over the entire sky. If all goes well, the spacecraft will start repeating its search over some portion of the sky.
Q: If you look at the NASA exoplanet archive site,
and ask for planets with "Discovery Facility" equal to "tess",
how many are there?
(The "Discovery Facility" column is at the very rightmost
edge of the page; you may need to scroll over to it)
 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.