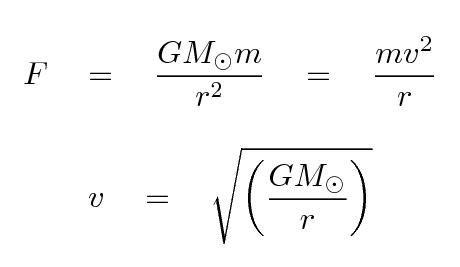
 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
In our solar system, most of the mass is concentrated in the very center. As a result, the velocity of planets in their orbits around the Sun decreases with distance from the Sun; one can derive a simple relationship from Newton's Law of Universal Gravitation:
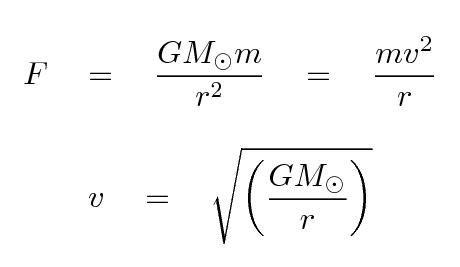
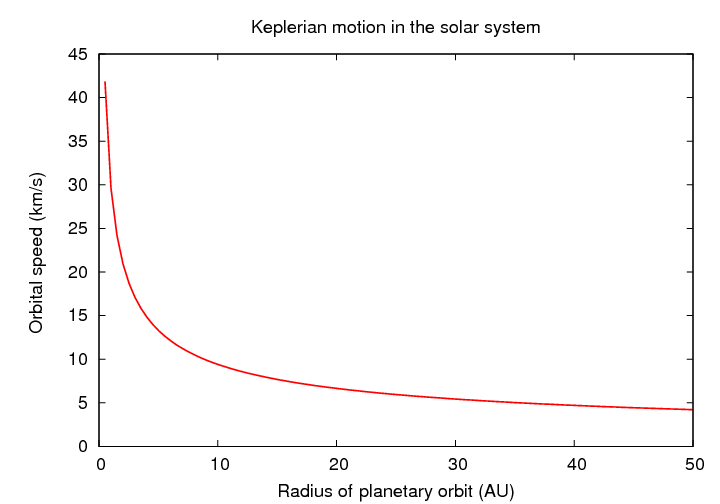
Note that this relationship has one obvious feature: the orbital speed DECREASES as one moves farther from the Sun. In fact, in decreases in a particular manner, but that's not so important right now.
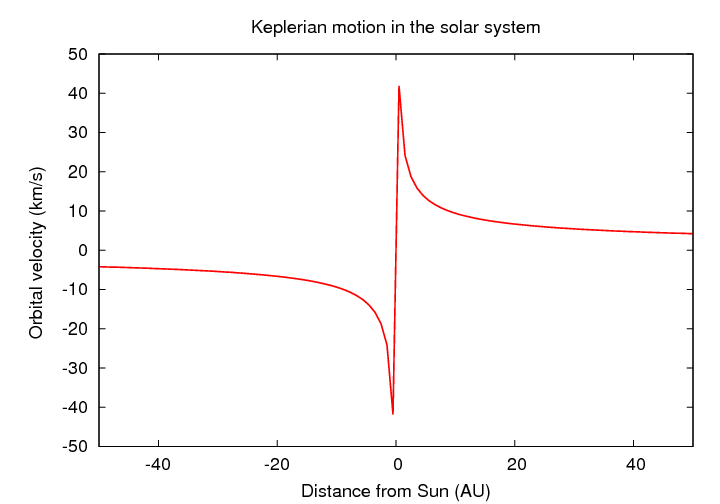
If we were to observe the solar system from a distant star, and measure the radial velocity of the planets, we'd see them move away from us (positive velocity) on one side of the Sun, and toward us (negative velocity) on the other side. A graph of radial velocity versus distance from the Sun would look like this:
Pictures of spiral galaxies suggest that most of their light resides near the center ...

... as do quantitative measurements of the surface brightness as a function of distance from the center.
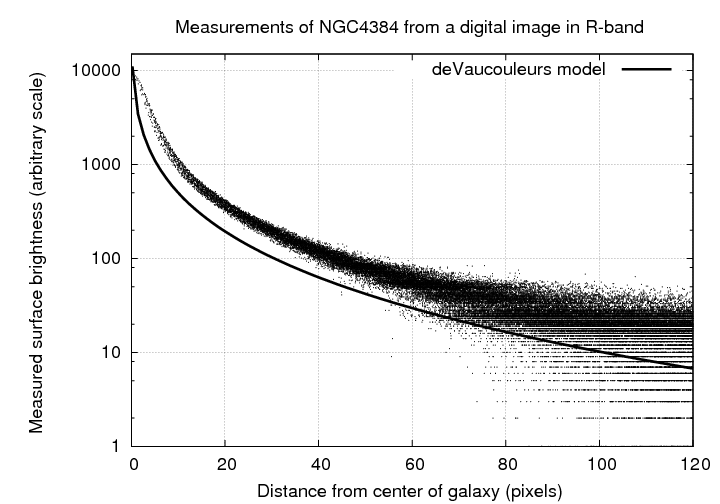
So -- do the stars and gas in spiral galaxies show the same Keplerian velocity pattern as planets in our Solar System?
In the 1970s, Vera Rubin and her colleagues W. Kent Ford, Jr., and Norbert Thonnard published a series of papers in which they demonstrated that many spiral galaxies had rotation curves which did NOT agree with the simple Keplerian model.
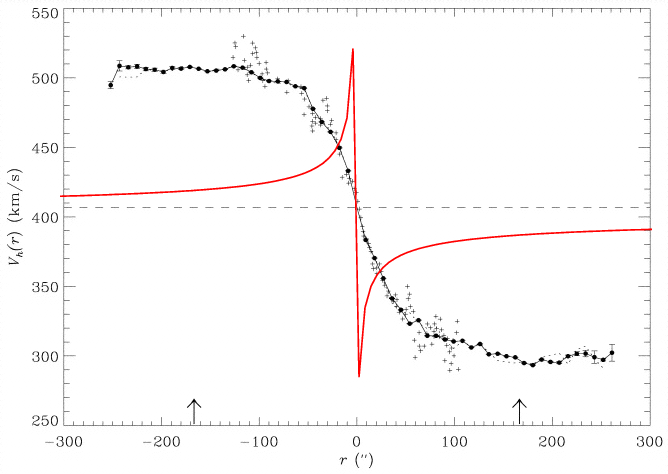
Figure taken from
Uson and Matthews, AJ 125, 2455 (2003)
and slightly modified
Many of the galaxies showed rotation curves which did not decrease at the largest measured radius; some were flat, such as NGC 7321, shown above, and others seemed to be rising, such as NGC 1421 and UGC 3691 in the figure below.
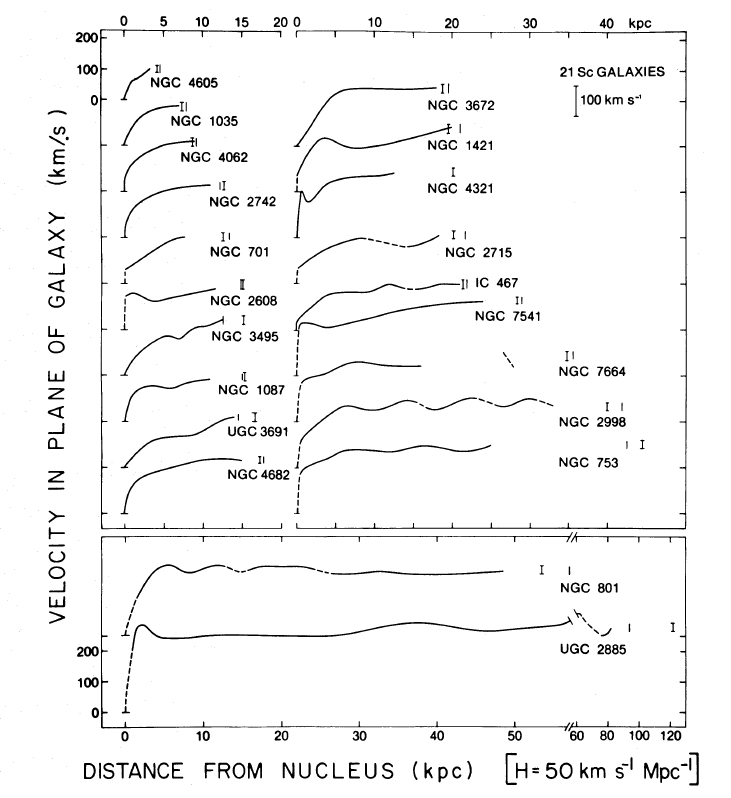
Figure taken from
Rubin, Ford and Thonnard, ApJ 238, 471 (1980)
This was very puzzling. The problem was that the dynamics of the galaxies just didn't agree with their appearance.
If a particle of mass m orbits within a spherical distribution of mass, then the net gravitational force on it depends only on the mass interior to its position, Mint. We can then derive a simple relationship between orbital velocity at some radius r and the amount of mass interior to that radius.

Now, if the orbital speed remains constant at large radii, then that must mean that
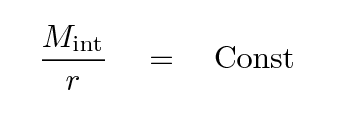
Q: If the ratio of interior mass to radius
is a constant, then what does that imply
for the density of material in the galaxy?
Write an equation for density as a function
of radius, ρ(r).

For a typical galaxy, the integrated light does not grow linearly with radius.
One can use the observed stellar population in a galaxy to derive the distribution of mass to compute the rotation curve for that distribution, and compare that rotation curve to the observations. They often don't come close to matching:
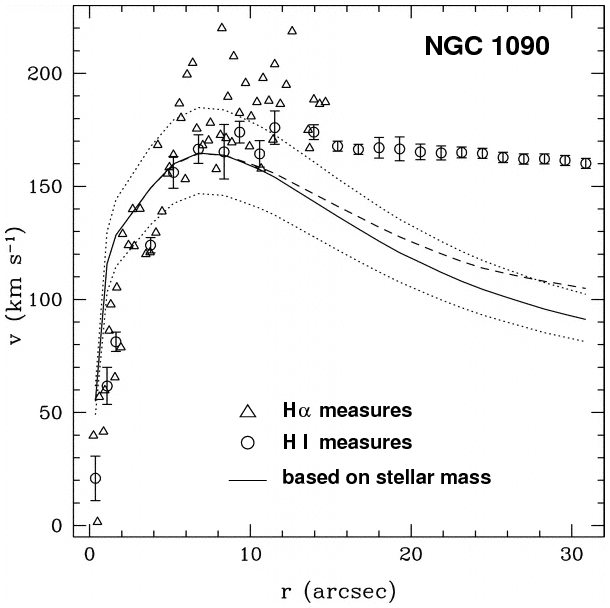
Figure taken from
Sassin, de Jong and Weiner, ApJ 643, 804 (2006)
and modified slightly
Thus, the problem: while the dynamics tell us that mass is growing linearly with distance, the light we measure does not. Since most of the light in a galaxy is emitted by stars, we can place some strong limits on the distribution of stars as a function of radius. The bottom line is that the visible mass in a galaxy cannot produce the observed rotation curves.
Astronomers sometimes express this idea using the term mass-to-light ratio (M/L). Consider a star like the Sun, of spectral type G2V.
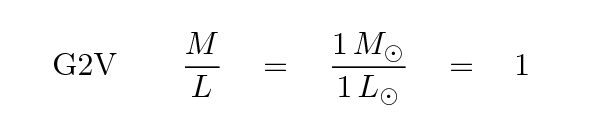
A more massive star, such as a B3, produces much more luminosity but has only a slightly larger mass; thus, it has a smaller mass-to-light ratio.
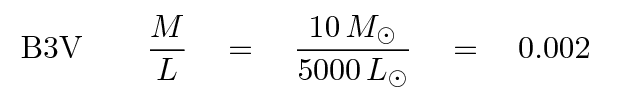
A low-mass star, such as an M2, produces much less luminosity, but has only a slightly smaller mass; its mass-to-light ratio is larger than the Sun's:
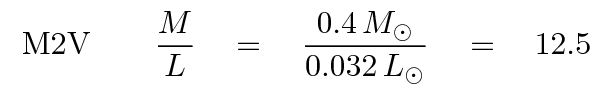
We can express the idea that the mass in the outer regions of a galaxy appears to grow much more rapidly than the light by saying that the mass-to-light ratio of the galaxy increases with radius.
Could the answer be as simple as a change in the stellar population with radius? Well, if so, then we'd expect to see a gradient in color with radius: galaxies would have to be much redder in their outer regions. Azzollini, Trujillo and Beckman (ApJ 679, L69, 2008) look at a set of galaxies of different types, running from spiral-ish ones on the left to elliptical-ish ones on the right.
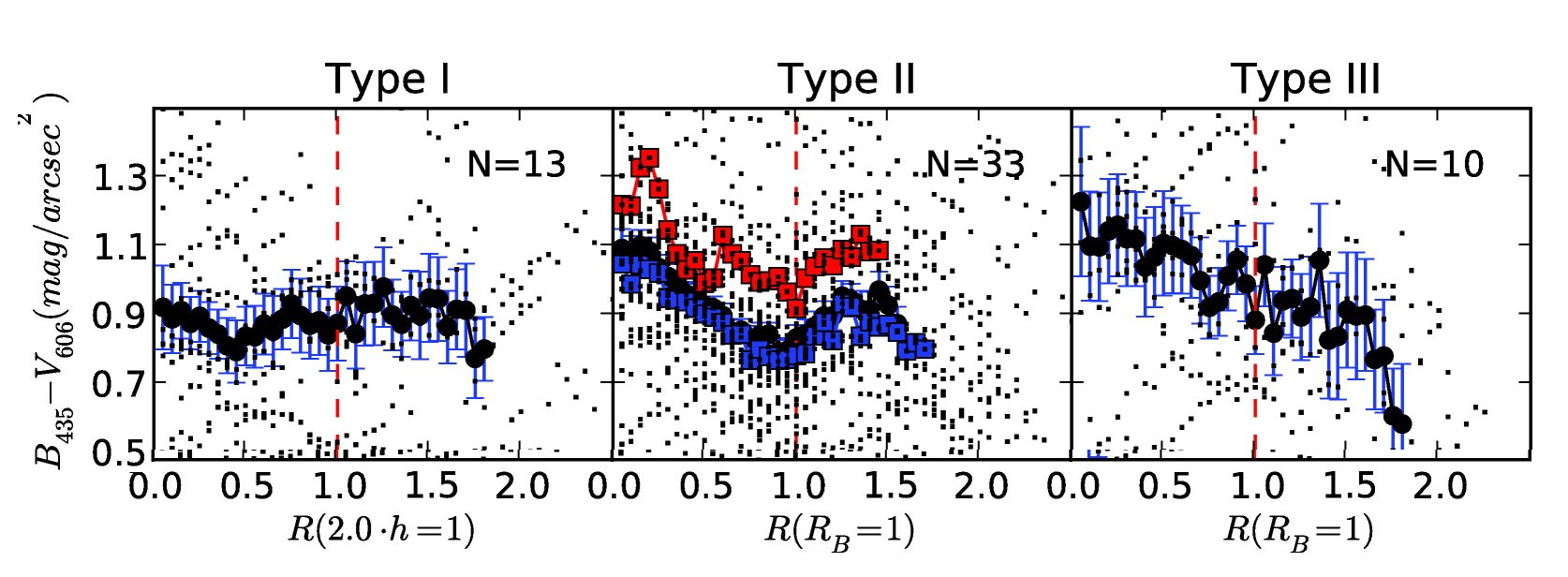
Figure taken from
Azzollini, Trujillo and Beckman (ApJ 679, L69, 2008)
We don't see such gradients, so it's not possible to explain the rotation curves with a change in the stellar population.
The motions of stars in elliptical galaxies are more complex than those in the disks of spiral galaxies; the shapes of the orbits are not simple circles, and there is no simple relationship between speed and distance from the center of the galaxy. One can use several different methods to study the distribution of mass within ellipticals:
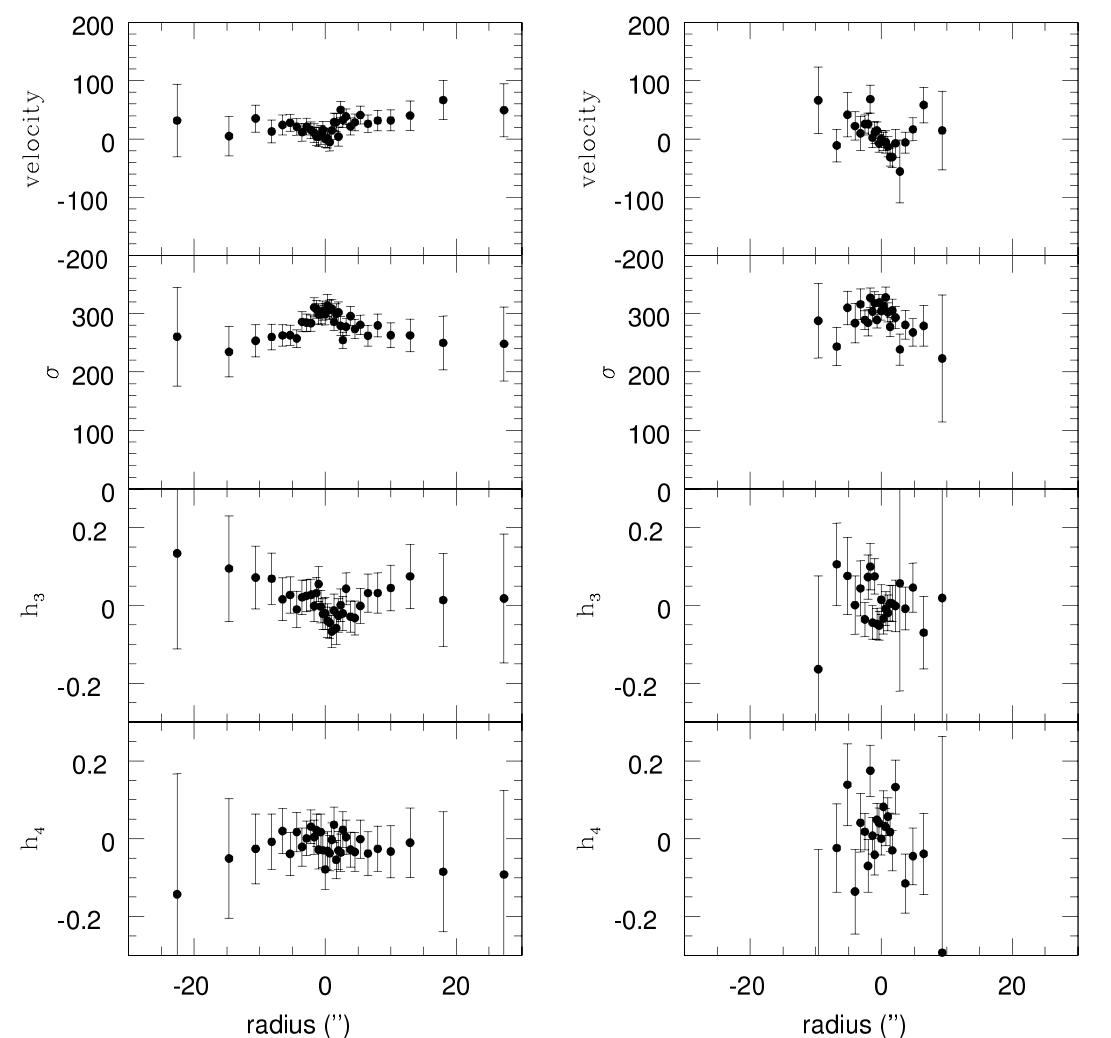
Figure taken from
Samurović and Danziger, MNRAS 363, 769 (2005)
In many cases, the inner regions of ellipticals have motions which can be explained entirely by the visible mass in those regions; but the outer regions often require some addition of dark matter. The elliptical NGC4105, for example, has a mass-to-light ratio which increases greatly at large radii,
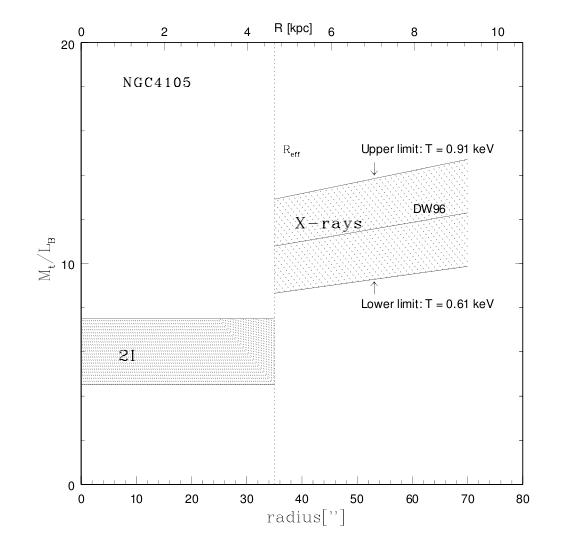
Figure taken from
Samurović and Danziger, MNRAS 363, 769 (2005)
... as does NGC 1344, in these measurements based on the motions of its planetary nebulae (squares), stars (asterisks).
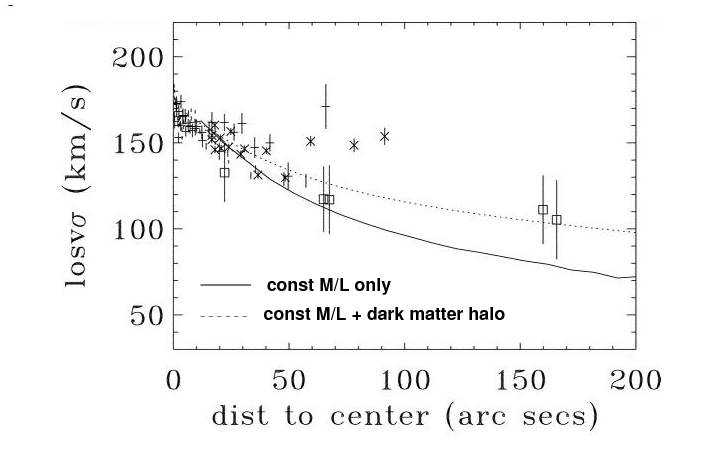
Figure taken from
Teodorescu et al., ApJ 635, 290 (2005)
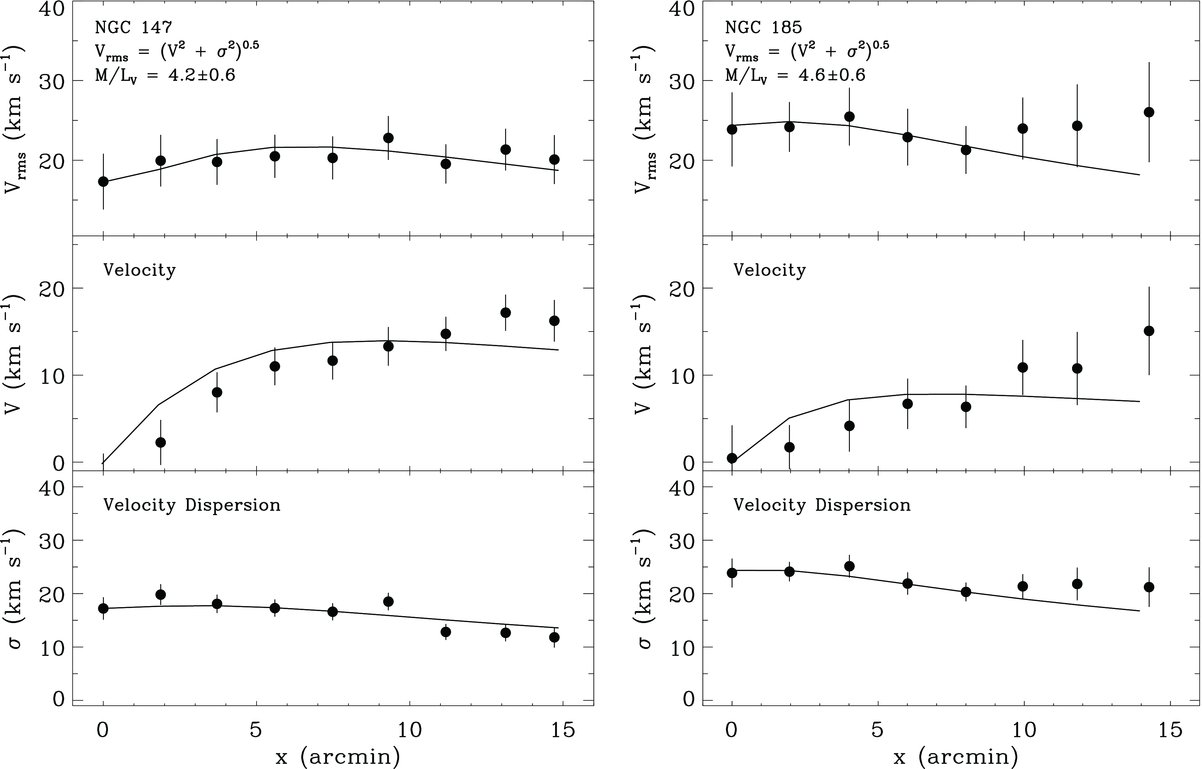
It does appear that some dwarf elliptical galaxies DON'T need dark matter to explain their dynamical properties. In the figure below, taken from Geha et al., ApJ 711, 361 (2010) , NGC 147, on the left, can be fit quite well by a model with a constant mass-to-light ratio of 4.2, which can be matched to its stellar population. NGC 185, on the other hand, needs a small increase in M/L with radius, but still might not require any significant amount of dark matter.
In the case of the Milky Way, we can actually measure all three components of the space velocity of some satellites, and so avoid having to assume some properties of the orbit. Piatek et al. (AJ 130, 95, 2005) measure the proper motion of many stars in the elusive Ursa Minor dwarf galaxy. Putting those motions together with earlier measurements of the radial velocities of some of these stars, they derive the following motions of the satellite. Note the units on the proper motions!
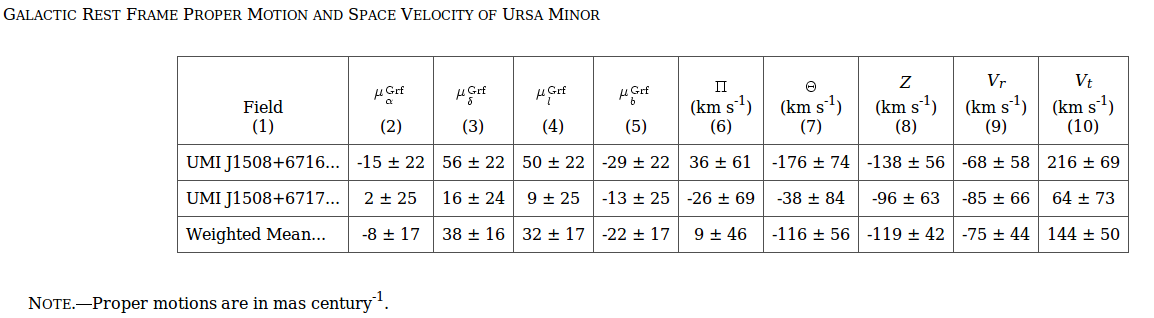
Table taken from
Piatek et al., AJ 130, 95 (2005)
This figure shows the motion of the Ursa Minor dwarf galaxy, based on its current velocity, extrapolated backward in time by 3 Gyr.

Figure taken from
Piatek et al., AJ 130, 95 (2005)
Using this motion, the authors derive a lower limit to the mass of the Milky Way at the distance of the Ursa Minor dwarf: 2.4 +/- 1.4 x 1011 solar masses within a radius of 78 kpc. This is consistent with a more comprehensive calculation of about 5 x 1011 solar masses out to a similar distance by Sakamoto et al., A&A 397, 899 (2003), which was based on measurements of many satellites. If we adopt an absolute magnitude of M(B) = -20.2 for the Milky Way Galaxy, following Hodge, PASP 95, 721 (1983), then we can derive an overall mass-to-light ratio of M/L(B) ~ 25 in solar units, out to a distance of 78 kpc. This is much larger than the ratio of a few that we would derive from the stellar population in the Milky Way; yet another piece of evidence for dark matter in our galaxy.
Watkins, Evans and An (MNRAS 406, 264, 2010) perform a similar analysis for both the Milky Way and M31. However, they use only radial velocities for some of the satellites, since it is very difficult to measure proper motions of objects at the distance of M31. They conclude

The apparent magnitude of the Andromeda Galaxy
in the B passband is m(B) = 4.36. It is roughly
d = 790 kpc from the Milky Way.
1. What is the absolute magnitude in B-band for M31?
2. What is the luminosity of M31 in B-band, expressed
in solar units?
3. What is the mass-to-light ratio in B-band for M31,
expressed in solar units?
The elliptical galaxy M49 is surrounded by hundreds of globular clusters; you can see several in these images from HST (2 images with 560 seconds of exposure each in F850LP filter).


The motions of those globular clusters are much faster than any model based on the stellar content of the galaxy can predict, as the figure below shows (lines are various models based on stellar mass of the galaxy, big dark circles are the measurements of the globular clusters).
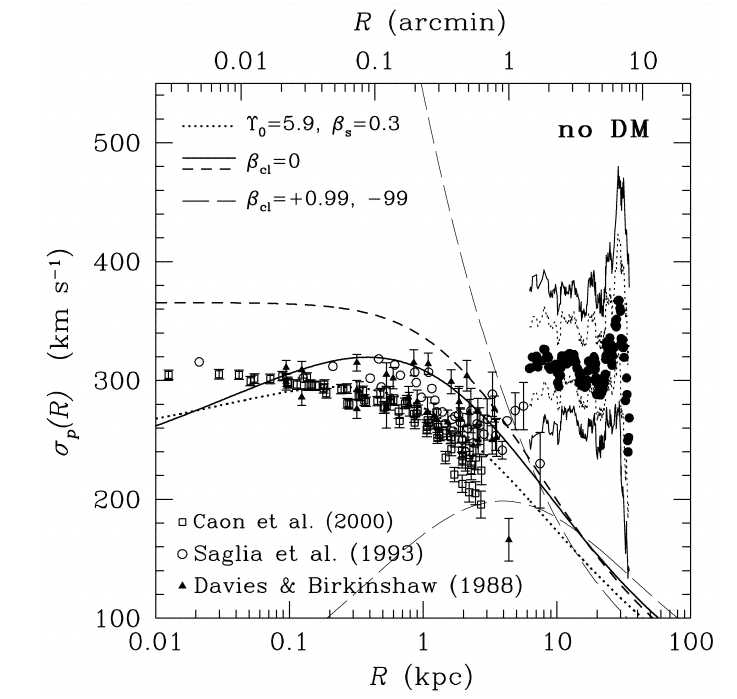
Figure taken from
Cote et al., ApJ 591, 850 (2003)
We can't see small satellites around other galaxies at large distances, but we can see many pairs of ordinary galaxies orbiting each other. The motions of the objects in these pairs are far too slow for us to measure -- the orbital time scales are in the hundreds of millions of years -- but we can easily measure the radial velocity of each galaxy. We can then perform statistical tests to estimate the masses of the galaxies in the pairs; we don't actually determine the mass of any one galaxy accurately, but we can gain some information on the average properties of galaxies in the set.
Chengalur, Salpeter and Terzian (ApJ 419, 30, 1993) measured the separations and radial velocities of many tens of pairs of galaxies, with projected separations up to about 1 Mpc
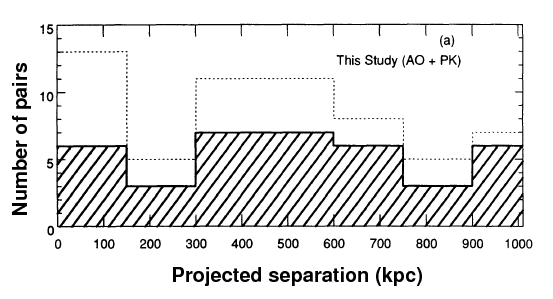
Figure taken from
Chengalur, Salpeter and Terzian (ApJ 419, 30, 1993)
with small modification
and velocities differing by up to about 400 km/s

Figure taken from
Chengalur, Salpeter and Terzian (ApJ 419, 30, 1993)
They selected pairs of galaxies which were most isolated from the perturbing effects of other galaxies and compared the observed properties to properties of pairs in dynamic simulations. They concluded that the typical mass of these pairs of galaxies was of order 1012 solar masses, consistent with the large values derived by other methods.
Junqueira and Chan (ApSS 279, 271, 2002) perform a similar analysis for a set of 46 pairs of elliptical galaxies. They find that the pairs have a typical mass of roughly 2 x 1012 solar masses, with a mass-to-light ratio of around 18.
A more recent application of this method can be found in Melnik, Elyiv and Vavilova (KPCB 25, 43, 2009) , who consider over 500 pairs and almost 300 triplets of isolated galaxies from the SDSS. They find that that the typical mass-to-light ratio is around 12 for the pairs, and around 44 for the triplets (with large uncertainties in each value). They provide a nice graphic which demonstrates the tendancy for the mass-to-light ratio to rise as one considers larger and larger systems.

Figure taken from
Melnik, Elyiv and Vavilova (KPCB 25, 43, 2009)
As we've seen, there is strong evidence that galaxies contain a great deal of dark matter: the gravitational mass appears to be larger than the visible mass by factors of a few to perhaps one hundred.
"Well," you might say, "that's not such a problem. That extra mass might be material which simply never turned into stars: warmish gas, perhaps, or very small rocks. There could be plenty of matter which just doesn't emit much electromagnetic radiation."
This sounds like a reasonable explanation, but there's a big problem: the agreement between models of nucleosynthesis soon after the Big Bang, and the observed amounts of the light elements created in that manner. The problem can be explained in several steps.
Throughout this section, I'll be discussing the "standard Big Bang Nucleosynthesis model" (SBBN). There are plenty of non-standard ones, with all sorts of differences.
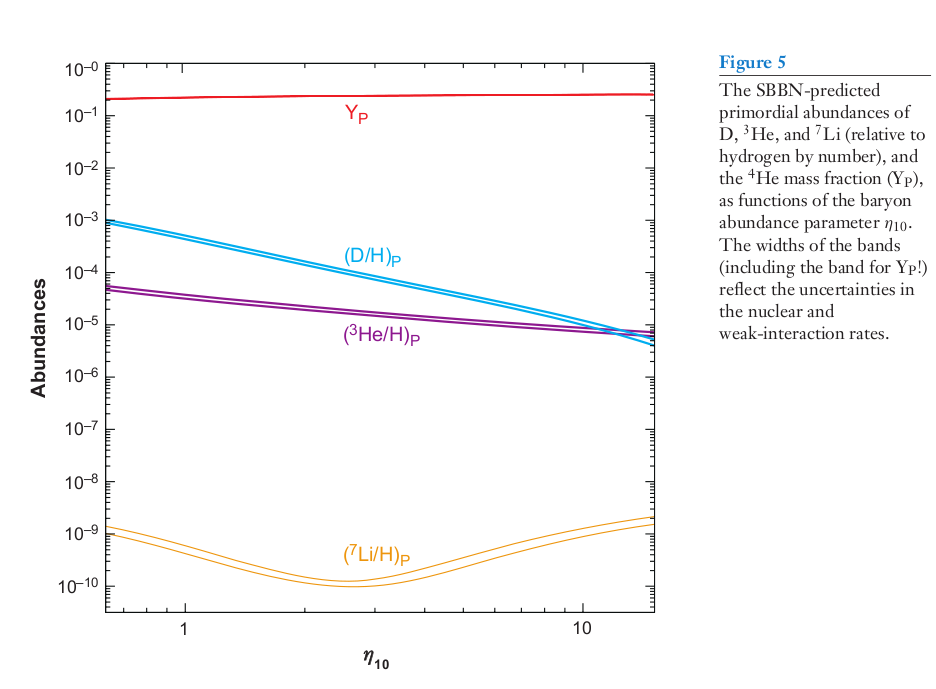
Figure taken from
Steigman, Ann. Rev. Nucl. Part. Sci. 57, 463 (2007)
Want to play the cosmology game using the graph above?
You'll need some
measurements of light-element abundances.
Consider these sources:
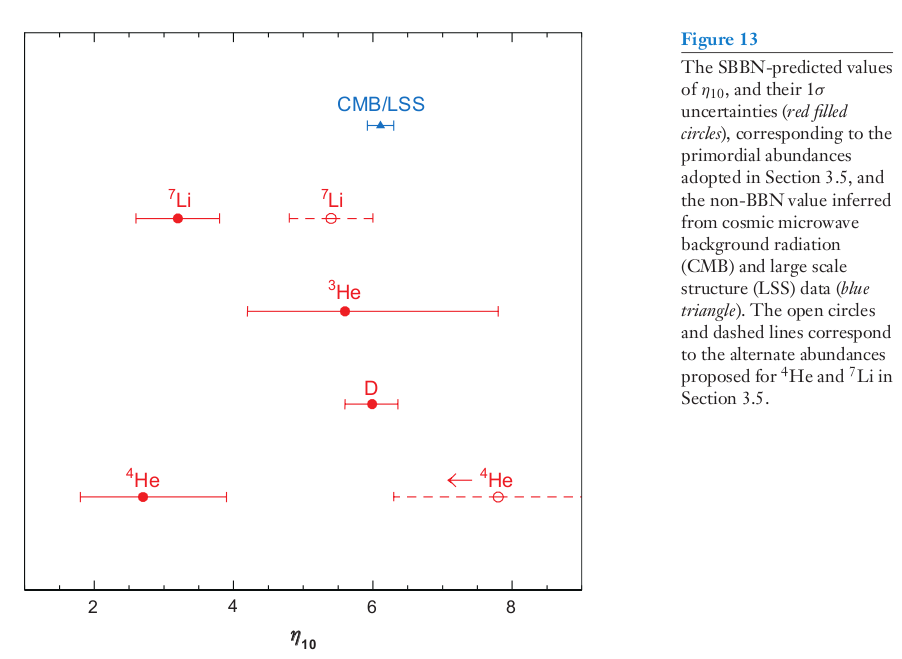
Figure taken from
Steigman, Ann. Rev. Nucl. Part. Sci. 57, 463 (2007)
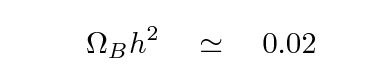
Measurements of fluctuations in the Cosmic Microwave Background (CMB) suggest that the overall baryon density has just about this same value -- a strong point in its favor. For example, the recent paper Planck 2013 results. XVI. Cosmological parameters provides a value of Ωbh2 = 0.0220.
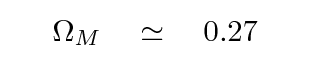
Planck 2013 results. XVI. Cosmological parameters provides a value of ΩM = 0.315 +/- 0.017.
The conclusion is uncomfortable, perhaps, but hard to avoid: the great majority of the gravitational forces in the universe are produced by matter which is not baryonic -- that is, not made up of ordinary atoms which consist of electrons, protons and neutrons. There must be a large amount of non-baryonic dark matter, which creates the majority of the gravitational forces on galaxy-sized scales.
 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.