
 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
In our quest to measure the distances to far-off galaxies and quasars, we have adopted a general method known as "the distance ladder." We start with very solid, reliable methods, but they only extend a small distance away from the Sun. Next, we use these accurate -- but short -- distances to calibrate slightly less reliable methods, which can extend our reach to larger distances. When even those methods fail, we turn to techniques with large uncertainties, because, well, that's all we can do.
The result is analogous to a rickety ladder, which grows more and more unsteady the farther up one climbs.

Wouldn't it be nice to find some clever new method that was BOTH very reliable AND could extend to large distances? If such a technique did exist, even for only a few special galaxies, we could use it as a check on the regular ladder, verifying that the multiple different methods yield accurate results; at least, in a few cases.
Today, we examine just such a method, which involves the analysis of radio measurements of megamasers -- special clouds of gas -- circling around the accretion disks of supermassive black holes. These megamasers are great because they provide DIRECT measurements of distance, avoiding the step-by-step approach of the distance ladder. Unfortunately, they only appear in a very, very few galaxies (6 at the current time), so they can't tell us about distances to galaxies or clusters in general. But they can, and do, allow us to check our other methods.
Let's concentrate on the most nearby and best-studied object in this category: NGC 4258. It looks like an ordinary spiral galaxy in the optical,
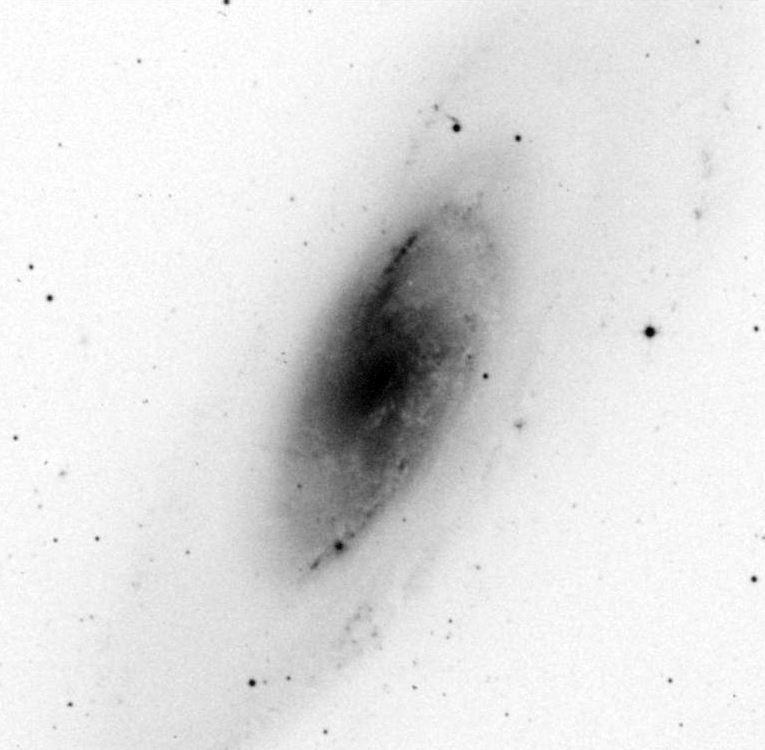
Image thanks to
the Aladin Sky Atlas
but X-ray and radio data indicate that there is a supermassive black hole at the center of the galaxy's bulge, making it an Active Galactic Nucleus (AGN). Now, lots of galaxies have AGN at their centers, but NGC 4258 is special: within the accretion disk of gas which orbits around the black hole at its center are certain clouds which have just the right combination of properties to create masers. In particular, water molecules making the transition 616-523 emit radiation at 22.235080 GHz (about 14 cm).
The important point about these masers, from our point of view, is that they act like tiny little spotlights: they are bright enough that we can measure VERY precisely the
How precise are the measurements? Combining signals from a number of telescopes -- the Very Large Array (VLA) and the Very Long Baseline Array (VLBA), each of which consists of many dishes spread over a large areas, and the Effelsberg 100-m single-dish telescope -- yields positions better than 0.1 milliarcsec, and velocities good to about 1 km/sec. Only masers provide the strong, unresolved signals needed to reach such high precisions.
Here's what we see at the center of the galaxy at these radio wavelengths: a set of unresolved sources, redshifted on one side of the center and blueshifted on the other. The intensity of the color in the figure is related to velocity: the fastest blobs are deep red and deep purple. The units on each axis are milli-arcseconds.

Figure taken from
Moran, ASP Conf Ser 395, 87 (2008)
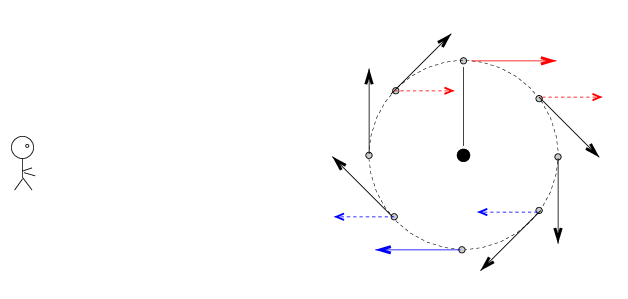
Q: Look at the pattern of the masers. Does it look like the simple Keplerian motion of clouds in a simple edge-on ring, all at the same distance from the center?
No, it doesn't. If all the clouds were in a ring, at a single distance from the central black hole, then we ought to see the largest speeds in the outermost blobs; but the observations show the largest speeds in the INNERMOST blobs.
It turns out that the geometry is pretty complex, something like this:

Figure taken from
Moran, ASP Conf Ser 395, 87 (2008)
The accretion disk is warped, and the masers we see are scattered throughout the disk, some much closer to the center than others. The clumps near the center are moving with the highest speeds.
Even though the geometry is rather complex, we can be pretty sure of several things:
and so
In other words, we can expect simple relationships between velocity v, orbital radius r, acceleration a, and the mass of the central black hole M:

Of course, we can't directly observe all these quantities; the only things we measure directly are the angular positions of the masers, relative to the central source, and their velocities.
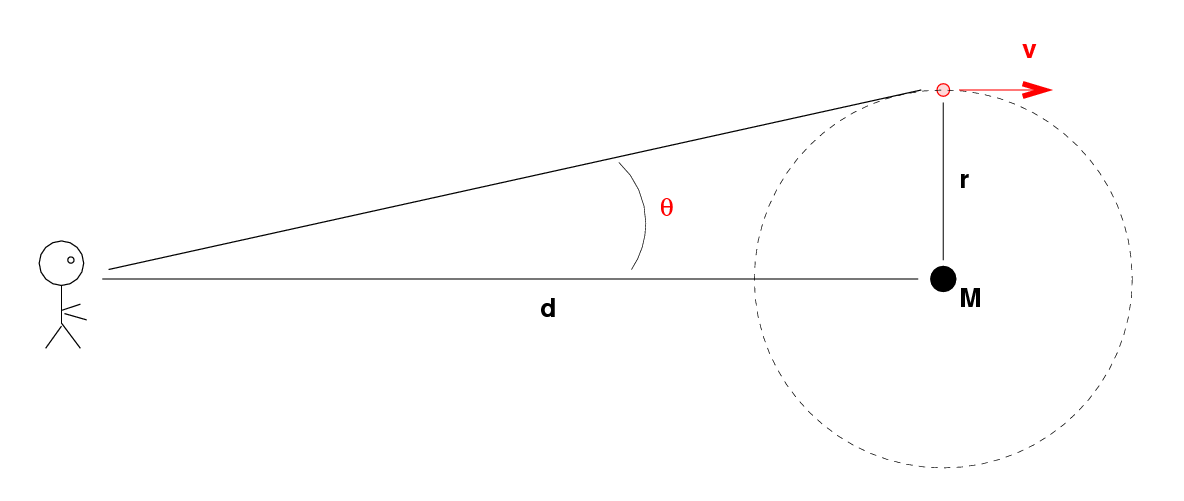
Q: Can we use the observed angle θ and radial velocity v
to figure out the distance d?
Well, let's see ... IF we knew the distance d, then we could compute the orbital radius r and the mass of the central object M.
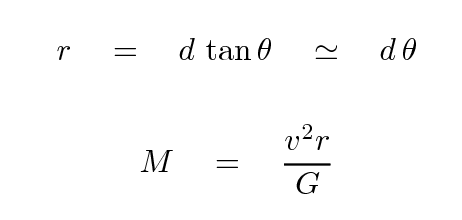
Let's play a little game. I'll choose one maser from the observed set, with the following properties:
radial velocity v = 1000 km/sec = 1.0 x 106 m/s rel to center
angular separation θ = 0.005 arcsec = 2.4 x 10-8 rad from center
Each student will just GUESS a distance, and then use that distance to compute the orbital radius r and mass M of the black hole.
distance d orbital radius central mass
(Mpc) r M
--------------------------------------------------------------------------
5 _________ __________ ___________
7 _________ __________ ___________
10 _________ __________ ___________
--------------------------------------------------------------------------
Hmmm. It seems that there is no unique solution: for any given distance, we can find an orbital radius and central mass which produce the observed quantities. In other words, we CANNOT determine the distance to NGC 4258 with this information alone. That should be no surprise. Both the orbital radius r and the central mass M depend linearly on the distance to the galaxy d.
But ... if we could find some observable quantity which had a DIFFERENT dependence on the distance, then we might be able to find a unique solution. Suppose we could measure the acceleration a of this little cloud of gas? Recall that the acceleration depends on the RECIPROCAL of the orbital radius

which means it also depends on the RECIPROCAL of the distance d to the galaxy. Aha! If we could observe the acceleration, we could break the degeneracy and solve for the distance to the galaxy.
Where should we look? Here are the locations of the masing clouds again, as observed by radio interferometers:

Figure taken from
Moran, ASP Conf Ser 395, 87 (2008)
Q: Which of these clouds might be the best choice
to detect the acceleration?
Why?
Just how big is this acceleration? Can we really measure it? Well, let's find out. Use your values to fill in the acceleration column of your table.
distance d orbital radius central mass acceleration
(Mpc) r M m/s2
--------------------------------------------------------------------------
3 7
5 25 x 10 AU 2.8 x 10 solar ___________
15 37
3.7 x 10 m 5.6 x 10 kg
3 7
7 35 x 10 AU 3.9 x 10 solar ___________
15 37
5.2 x 10 m 7.9 x 10 kg
3 7
10 50 x 10 AU 5.6 x 10 solar ___________
15 37
7.5 x 10 m 11.2 x 10 kg
--------------------------------------------------------------------------
Those values seem really small. How could we measure such tiny accelerations? Well, the good thing about accelerations is that they can accumulate over time into large changes in velocity.
Q: Suppose we measure the velocity of one cloud now,
and then again after one year has passed.
How large would the change in velocity be?
Radio astronomers have patiently monitored this galaxy for many years, watching for exactly these expected changes in velocity of the individual clouds. Below is a small sample of their results; the numbers in the upper-right corner of each panel refer to the number of days since 1994 Apr 19. Each cloud is drawn in a different color to help you follow the evolution of its velocity.
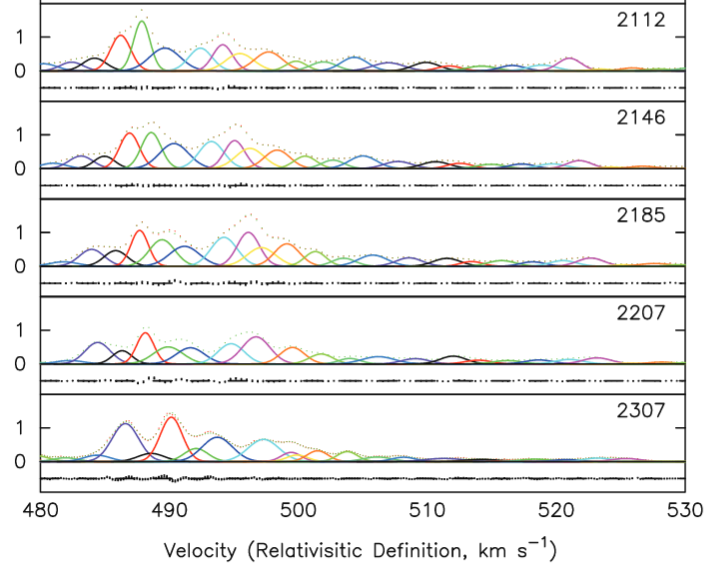
Modified from Figure 5 of
Humphreys et al., ApJ 672, 800 (2008)
Q: Pick one cloud and compute its acceleration.
So, as you can see, we CAN measure accelerations of the size produced by orbital motion around the central black hole. In theory, then, we can solve for the distance to the galaxy.
In practice, this is complicated because the clouds are all at different distances from the center, because the disk is not perfectly edge-on, and because it appears to be warped slightly. There are ... a number of parameters one must determine, not just the distance. But some astronomers have done all that work and conclude:

Abstract from
Humpheys et al., ApJ 775, 13 (2013),
just in case you couldn't figure it out for yourself.
The reason that I've spent so much time describing this one galaxy is that it provides a nearly geometric distance to an object far, far beyond the Milky Way. This distance does NOT depend on previous steps of the distance ladder (well, aside from the distance to the Sun). That means that we can use NGC 4258 to check our other methods of distance measurements -- at least, the methods that can reach it.

In addition, some radio astronomers are seeking out other examples of AGN with megamasers in their accretion disks, in order to use the same technique to measure their distances. The Megamaser Cosmology Project has published studies of five other galaxies, all much more distant than NGC 4258.
| Galaxy | Distance (Mpc) | Reference |
|---|---|---|
| NGC 3789 | 49.6 +/- 5.1 | Braatz et al., ApJ 718, 657 (2010) |
| NGC 6264 | 144 +/- 19 | Kuo et al., ApJ 767, 155 (2013) |
| NGC 6323 | 73 +26-22 | Kuo et al., ApJ 800, 26 (2015) |
| NGC 5765b | 126.3 +/- 11.6 | Gao et al., ApJ 817, 128 (2016) |
| CGCG 074-064 | 87.6 +/- 7.6 | Pesce et al., ApJ 890, 118 (2020) |
Since these other galaxies are so much more distant than NGC 4258, our measurements of the exact positions and velocities of their masers are less exact. As a result, the distances we derive for them have much larger uncertainties.
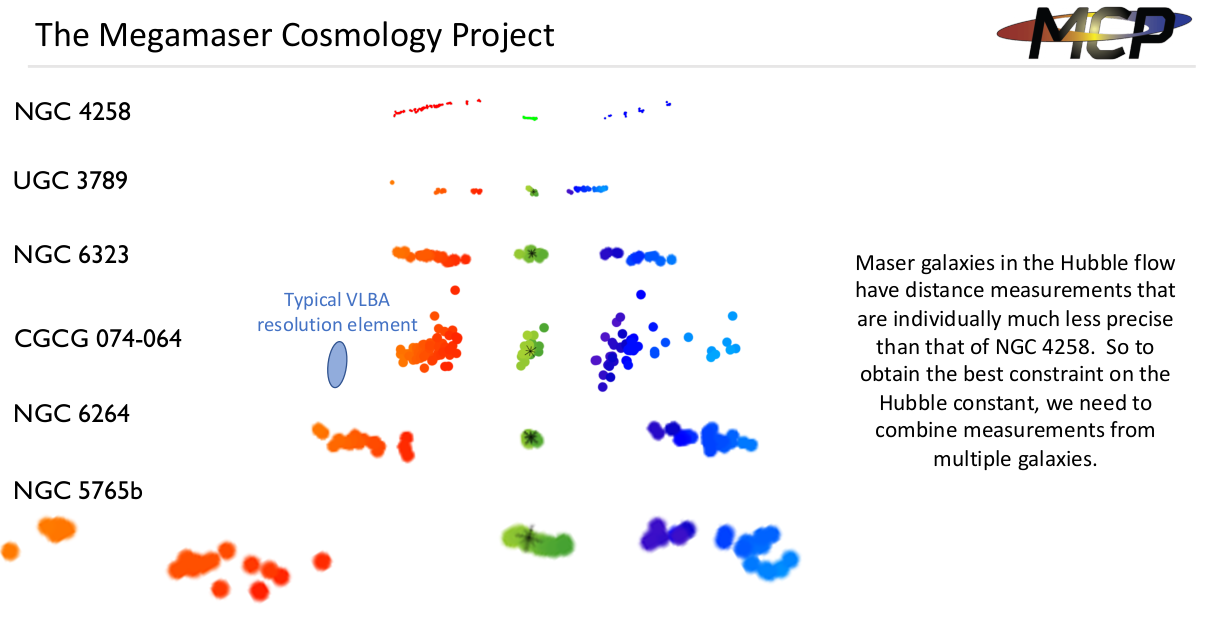
Slide taken from
a presentation by Dom Pesce in 2020
Although the number of objects we can measure with this method is very small, the DIRECT distances we can derive will serve as extremely valuable checks and calibrators of other techniques.
Moreover, recent developments in radio astronomy have generated hope that we might improve the quality of our measurements of megamasers in accretion disks. All of the existing studies have involved measurements of a molecular transition which emits radio waves of frequency 22 GHz, or about 14 cm. New telescopes, such as the Atacama Large Millimeter/sub-millimeter Array (ALMA), are able to work effectively at higher frequencies (or shorter wavelengths). In particular, the line involving the transition 31,3 - 22,0 seems particular promising. It produces light with a frequency of about 183 GHz, or a wavelength of about 1.6 mm.
The Bad News is that, at the moment, astronomers have not succeeded in combining the signals from dishes located very far apart (on different continents) at these higher frequencies. In other words, the current Very Long Baseline Array (VLBA) system cannot work at these frequencies yet. That means that we cannot create the detailed radio images which are necessary to apply this method to estimate the distances to galaxies.
The Good News is that, IF the VLBA is modified so that it can observe at these frequencies, it would in theory be able to make measurements of the masers with even higher angular resolution -- roughly a factor of 10 more precise. In that case, the quality of our distances to these crucial checkpoints would improve greatly.
 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.