Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
This course focuses on stars: what we can see when we observe them, and how they work. We'll concentrate on ordinary, "boring" stars like the Sun, and touch only briefly on the oh-so-cool neutron stars and black holes which are created by a tiny fraction of the stellar population. Our subjects will almost entirely be located within our own Milky Way Galaxy; in fact, within our local neighborhood with the Milky Way. The closer they are, the easier it is to study them.
We can break up the course into four stages:
Our guides throughout the semester will be Professors Carroll and Ostlie, who wrote the textbook An Introduction to Modern Astrophysics. I consider this a very useful textbook, both because it covers a wide range of topics, and because I can understand most of its explanations. I have copies of the first edition, which differs in a few minor respects from the second edition. If at some point there appears to be a disagreement between something I say or write and the book you are reading, it may be due to this edition mis-match; or, more likely, I could have just screwed up. Either way, please let me know.
The list of topics we'll cover can be seen on the main course webpage. If you are interested in the rules of the course, when we meet, my contact information, the breakdown of credit toward your final grade, and other such items, check out the outline/syllabus for the course. Some class materials, such as drafts on the student presentations and comments on those drafts, can be found at the myCourses page for this course.
Student presentations? Ah, yes. On the final two days of the class, students will take turns giving 5-minute presentations on a star of their choice. We will discuss these presentations after the midterm, but the basic idea is to find some star which you find interesting; maybe because it blew up, or because it's REALLY hot -- or maybe it's REALLY cool (for a star). Perhaps you might hear about a binary star system in which one member is feeding off its partner, or discover the story behind van Manaan, and why someone named a star after him. In any case, you will create a draft of your presentation several weeks before the end of the semester and submit it to the class for comments. Students will look it over and make suggestions, and you will incorporate (or not) their comments into the final form of your presentation.
This presentation will account for a good chunk of your grade. The rest will come from the usual suspects: homework, a midterm, and a final exam.
Before we can turn to stars, however, we need to spend a bit of time sharpening the tools we will use to study them. As you know, we can't collect samples of star-stuff to study in the labs here on Earth, even for our own Sun.
Okay, I lied. NASA's Genesis mission actually did collect particles of the solar wind in space and return them to the Earth ... well, with a few minor issues.
For more on the sad story of the sample return, see a short history, with physics.
Therefore, we must rely on electomagnetic radiation as our sole(*) messenger from the celestial realm. We will start this class by reviewing some of the properties of light.
(*) Well, I lied again. There are actually THREE other messengers which have travelled from the far depths of space to our instruments on Earth, carrying bits of information about stars. Can you name them?
- neutrinos -- from a single source: SN 1987A
- gravitational waves -- from a dozen-ish very unusual stellar remnants
- radioactive atoms (or their decay products) blown out of a handful of nearby supernovae, millions of years ago
So, for all practical purposes, we must rely on light.
Let's start with the basics. Consider a single photon, of some given frequency or wavelength. The energy of that photon is
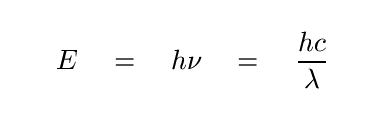
In the optical regime, which is where we will spend the bulk of this course, astronomers usually describe photons by their wavelengths, rather than their frequencies (radio astronomers do it the other way around, and high-energy folk label photons by their energy). So the second form is the one I'll often use in discussions.
Moreover, let me warn you that optical astronomers also prefer to use a rather unusual unit to measure wavelength: the Angstrom (Å), which is 10-10 meters. Let's do a simple example:
Q: What is the energy of a photon in the middle of the optical range,
with a wavelength of 5000 Å?
But light is not always best described as a photon. There are times when it is convenient to consider light as a continuous wave. What's the energy of a wave of light?
Well, the "energy" of a wave isn't a very well-defined quantity; after all, the wave may exist over a considerable distance, but we can only sample it in one location. A better way to deal with a wave is to measure the power of a wave: the amount of energy that it transmits across some area during some period of time. A common way to compute the power of a wave is known as the Poynting vector:
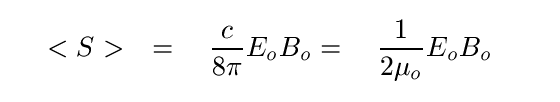
where Eo and Bo are the maximum amplitudes of the electric and magnetic fields of the wave, respectively. Note that the units of this quantity are different in the two expressions above: the first version yields the cgs units erg/cm2-s, while the second yields the MKS units W/m2.
We will see the Poynting vector later on in this course when we discuss radiation pressure, so let's introduce that now. "Radiation pressure" is another way to say "force exerted over some area", and so to compute the force exerted by an electromagnetic wave which strikes some object, we must include that area. The following expression is appropriate if the wave is completely absorbed by its target,
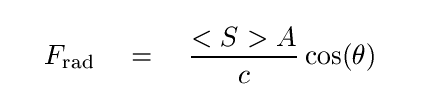
but if the wave is completely reflected, we must include a factor of two (one for stopping the wave, one for sending it back when it came) and square the cosine term, since the wave will bounce off at the same angle θ.
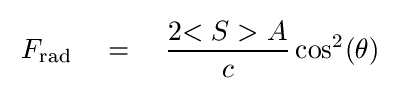
In order to compute the force associated with individual photons striking a target, we need to write the momentum of a single photon:
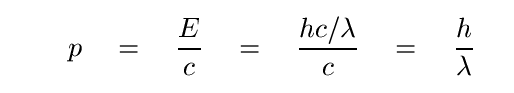
Recall that integrating force over time yields impulse -- a change in momentum during that time period. So, we can go the other way: a change in momentum over some period of time can be equated to a force. Suppose that N photons should strike a target over some time t, and all be absorbed by the target. Their transfer of momentum over that time can be described as a force -- the force of radiation pressure.
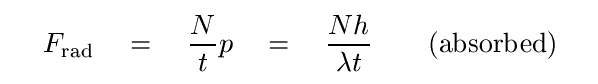
If the photons are reflected perfectly in the direction from which they came, then the force is simply twice as large:
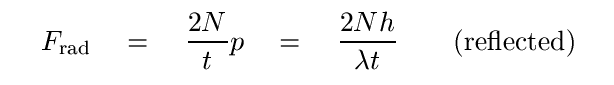
Radiation pressure calculated in this manner can be important in several situations, such as
Superman, it is said, acquires his super-powers from our yellow Sun. (Yes, yes, there are several inconsistent explanations in different comics, but let's go with this)
Page taken from
Action Comics 300
Suppose that Superman needs to leap over a very tall building -- one of height h = 500 m. Let's estimate that Superman has a mass m = 90 kg and a chunky rectangular body, 2 m tall and 1 m wide (he has very broad shoulders).
Q: How much energy will it take for Superman to vault to the
top of the building?
Q: Assume that the Sun emits all its energy in the form of
photons with wavelength 5000 Angstroms.
How many photons are required to provide this amount
of energy?
Q: The solar luminosity is about 3.8 x 1026 Joules per second.
How many photons does it emit per second?
How many photons strike one square meter of the Earth
per second?
Assuming that Superman lies motionless on the ground at noon,
how long will it take the Sun to charge Superman for his jump?
Another property of electromagnetic radiation which will we encounter very frequenty in our study of stars is blackbody radiation, which is emitted by any "sufficiently dense" material. What does that mean? Basically, any solid, liquid, or gaseous object so thick that one can't see through it. Gold, silver, carbon, rocks, ice cubes, lava -- the composition doesn't matter. All you need to know is the temperature. If you heat the material to a temperature T, any surface of area A will emit the same amount of electromagnetic waves (ignoring small factors of order unity which are lumped into a quantity called "emissivity").
Just knowing that much is pretty useful. But what's even better is that if one doubles the temperture, from T to 2T, then the amount of energy emitted doesn't just double, or quadruple -- it increases by a factor of 24. So this blackbody radiation is VERY sensitive to temperature.
One can sum it all up by writing
where σ = 5.67 x 10-8 W/m2K4 is the Stefan-Boltzmann constant, and A the area in square meters.
So figuring out the total power emitted by a blackbody is easy-peasy.
Q: What would be the power emitted by the body of a live human being,
if we suspended it in some measuring chamber?
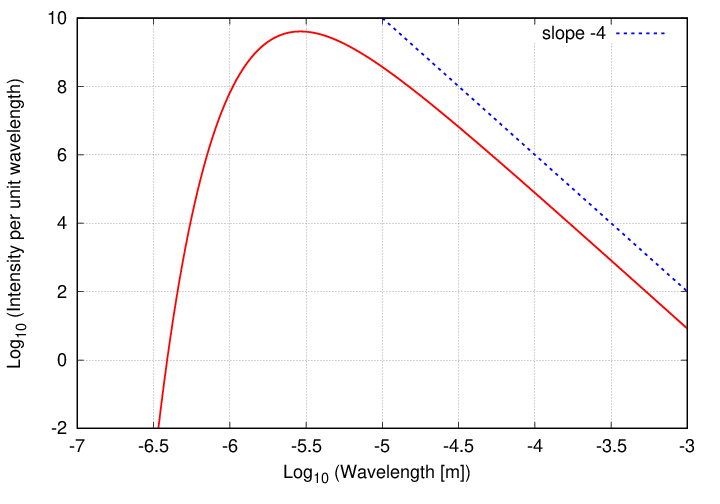
What is not so easy is calculating exactly how much of this power is emitted at any particular wavelength or frequency. Well, measuring the power at any particular wavelength isn't so bad, but determining a functional form for the resulting relationship is quite a puzzle. For example, if we graph the intensity as a function of wavelength (the units might be ergs per sq.cm. per second per Angstrom, or Watts per sq. m. per second per m) on a logarithmic scale, we see this:
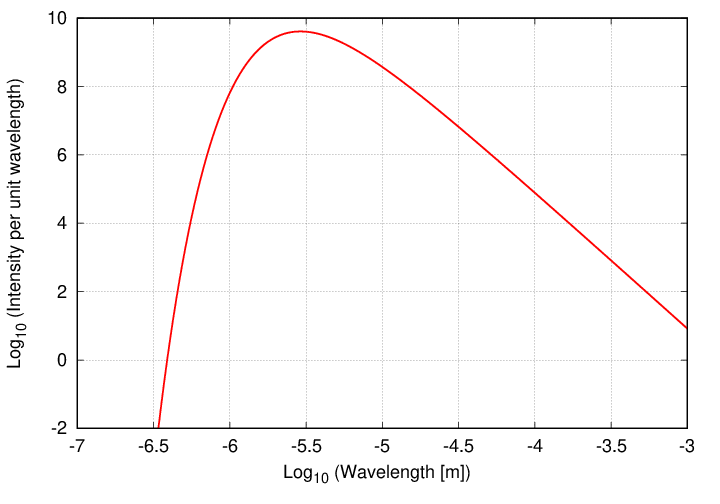
The graph falls into two sections:
One can describe this curve mathematically by combining an exponential function (look in the denominator) and a power law (look in the numerator).
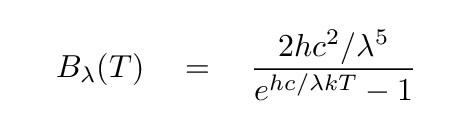
Q: What happens to this function when wavelength becomes very small?
Q: What happens to this function when wavelength becomes very large?
In particular, what is the slope of the line at long wavelengths?
Now, one can also depict the intensity of radiation as a function of frequency.
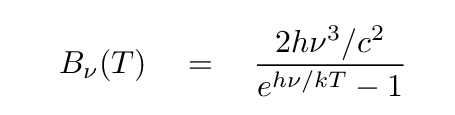
In that case, the units might be ergs per sq.cm. per second per Hz, or Watts per sq. meter per second per Hz. If we graph this equation, we see a familiar pattern -- but with two changes.
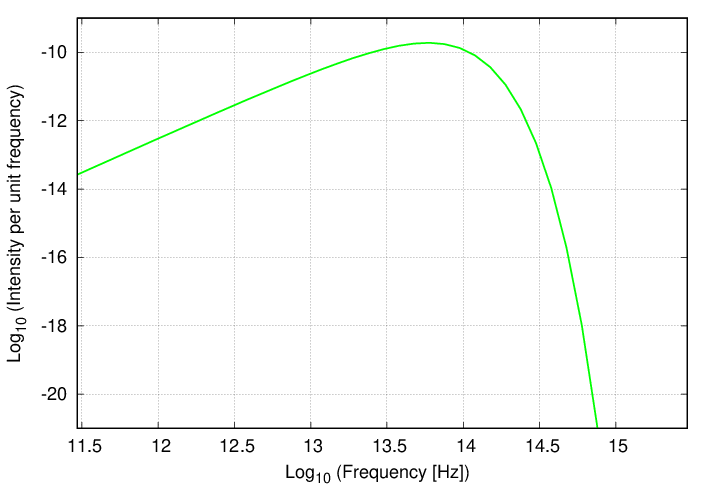
Q: What is the first difference between this and the graph
as a function of wavelength?
Q: What is the second difference?
The first difference is that the graph is reversed left-for-right, since high frequencies correspond to small wavelengths, and vice versa. But the shape is the same ... almost. Because the second difference is that, although the behavior at the low-energy end (this time on the left side of the graph) is once again a power law, the SLOPE of that power law is different.
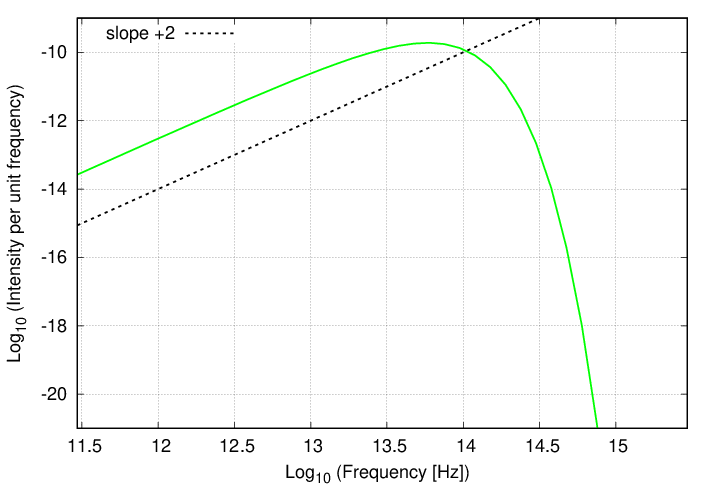
Q: Can you derive the slope of this power law?
For the most part, in this course, we'll express intensity as a function of wavelength.
Now, there are two other features of the blackbody spectrum which are noteworthy. If one compares the spectra of objects of different temperatures, one sees that
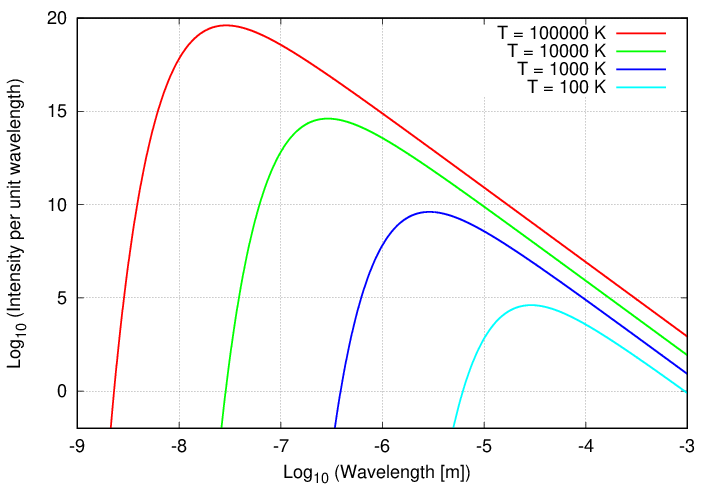
There is a simple relationship between temperature and the wavelength of the peak.
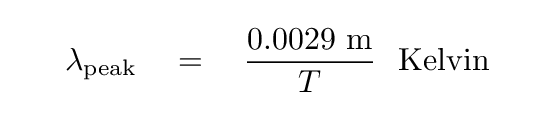
Q: What is the peak wavelength for a star like the Sun?
Q: What is the peak wavelength for a live human being?
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.