 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
As mentioned in an earlier lecture, scientists have good evidence that our universe is expanding on very large scales. Not in ordinary, every-day life: the average human is still under two meters tall, and the walk from the Infinity Quad to the SAU still takes about three minutes. But if one looks at galaxies and clusters of galaxies, one will find that they are on average moving away from each other.
Not only that, but the speed of recession increases with distance between objects -- just as it does for raisins embedded in a lump of rising dough.
That connection between velocity and distance is measured by a quantity called the Hubble Constant, or H0 for short. The larger the value of H0, the faster galaxies separated by some specific distance move away from each other.
This parameter clearly is an important piece to the cosmological puzzle. In the simplest models, the future of the universe depends on a competition between two factors: the speed with which the universe is expanding (given by H0) and the gravitational forces between the galaxies and other matter. In those models, the value of H0 can help us to understand the ultimate fate of our universe.
In more complicated cosmological models, other factors come into play, and the Hubble Constant becomes somewhat less important to the overall story.
Moreover, in nearly any cosmological model, the value of the Hubble Constant is closely related to the current age of the universe. If we want to know how long ago our universe came into existence, we need to know the value of H0.
Well, if it's so fundamental to our understanding of the universe, we should try to figure out its value. How can we measure his parameter?
In theory, it's pretty simple to do. We can follow the example of Edwin Hubble himself, in his ground-breaking paper
In Figure 1, Hubble plotted the radial velocity of a set of galaxies against their distances.
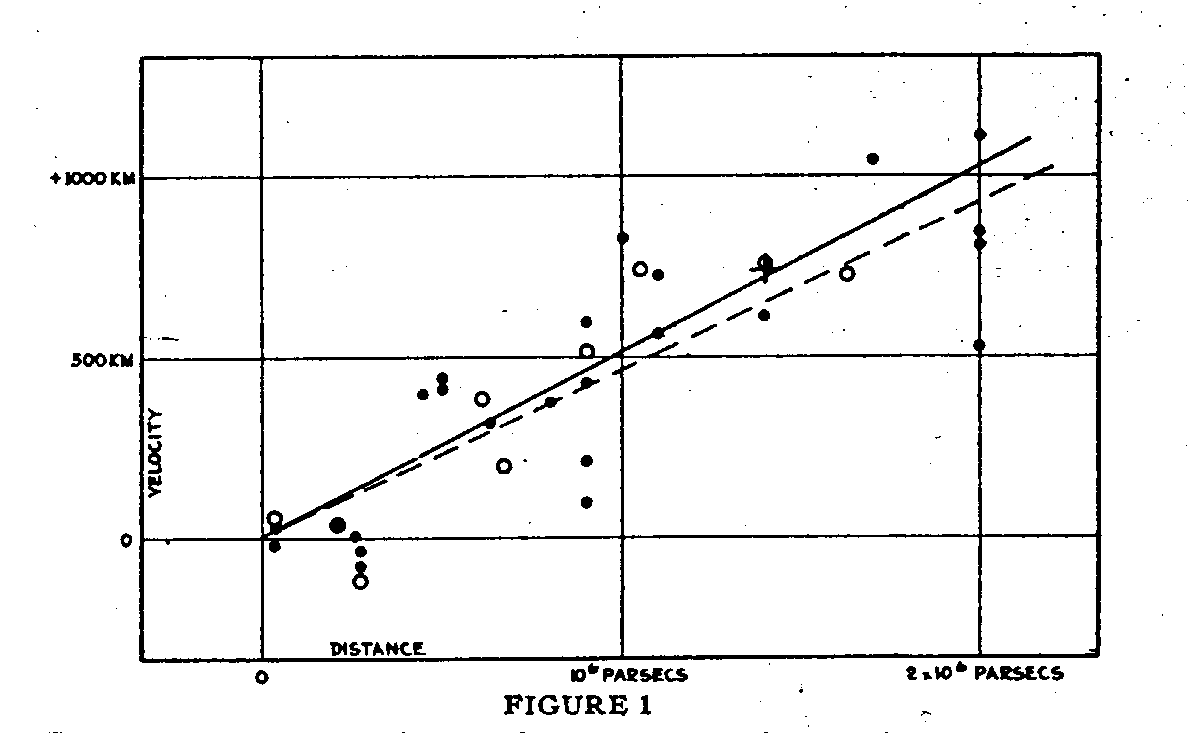
Figure 1 taken from
Hubble, PNAS 15, 168 (1929)
Q: What are the units of distance?
Q: What are the units of radial velocity?
(careful -- the graph is labelled poorly)
Q: What is the slope -- both size and units?
Now, if one examines the Hubble Constant carefully, one will note that the units are a bit redundant. There are units of length (km) on the top of the expression, and other units of length (Mpc) on the bottom.
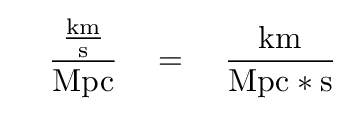
We can simplify this expression by converting both km and Mpc to meters, and then cancelling the meters.
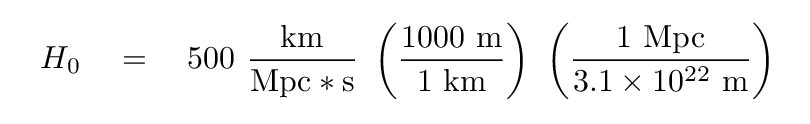
Q: What is the value of H0 after we simplify in this way?
Hmmm. The simplified version has units of inverse time -- one over seconds. It is possible to show that the age of the universe is related to this inverse time. In fact, to a fair degree (within a factor of two or so), the age of the universe is just the reciprocal of the Hubble Constant.

Q: Based on our value of H0 derived above, what is the age
of the universe?
Q: Do you see any problems with this age?
Hubble's original estimate, published in 1929, suffered from a number of errors, all related to his values for the distances to other galaxies. Hubble did the best he could with the information at his disposal, but the telescopes and photographs of the time could not provide data of sufficient quality to allow good measurements. For example, some of the objects Hubble classified as "stars" in other galaxies were actually glowing clouds of gas lit up by hundreds or thousands of stars, which we now call "HII regions."
Over the past century, advances in telescope and detector technology, plus additional methods of estimating distances, have allowed astronomers to revise the distances to those galaxies first used by Hubble. Let's use some of those revised distances to make our own, improved, estimate of the Hubble Constant.

Distances to galaxies measured via the surface-brightness-fluctuations (SBF)
technique, given by
Tonry et al., ApJ 475, 399, 1997
Q: What is the value of the Hubble Constant based on this dataset? Q: What is the age of the universe, based on this dataset?
Clearly, there's a big difference between the values of the Hubble Constant, and the consequently derived ages of the universe, between 1929 and now. But why? What changed? There are two possibilities:
The first option, that changes in radial velocity is responsible for the difference, is not correct. Measuring the radial velocity of a (nearby) galaxy is pretty straightforward: acquire a spectrum, identify some absorption lines, measure their shift from the rest wavelengths, and compute a velocity. Acquiring a good spectrum can take a lot of time and effort, especially in the bad old days of photographic plates,
During the past year two spectrograms of N. G. C. 7619 were obtained with Cassegrain spectrograph VI attached to the 100-inch telescope. This spectrograph has a 24-inch collimating lens, two prisms, and a 3-inch camera, and gives a dispersion of 183 Angstroms per millimeter at 4500. The exposure times for the spectrograms were 33 (hours) and 45 (hours) , respectively.
Quotation taken from Humason, ApJ 74, 35 (1931)
but all the subsequent work is relatively easy. The velocities measured by Hubble and his collaborators back in the 1910s and 1920s are pretty much the same as those that we measure for those same galaxies today.
The explanation for the big change in the Hubble Constant is that the distances estimated by Hubble were much, much smaller than those we derive using modern equipment and methods.

In other words, our ability to measure the age of our universe is tied directly to the quality of our measurements of DISTANCE to other galaxies.
And how do we do that? How can we measure the distance to galaxies beyond our Milky Way? The answer, for a long time, has been to build a distance ladder, using one method for nearby objects to calibrate a different method for more distant ones.
For example, the step in our ladder might involve
This is so reliable -- it's based on geometry, after all -- that the first step in our ladder is firm and strong.
The next step adds distances to eclipsing binary stars; some of the parameters are securely based on geometry, but others require fitting models of stellar atmospheres to spectra of the binary components. Those models are based in part on observations of very nearby stars with parallax.
That means that the second step in our ladder is a bit less secure than the first.

Using eclipsing binary stars, we can determine the distance to the Large Magellanic Cloud (LMC). Since the LMC has plenty of RR Lyrae and Cepheid stars, we can calibrate the absolute magnitudes of these stars using the LMC distance. Any errors in the distance to the LMC will, of course, propagate into errors in the absolute magnitudes of the pulsing stars.

We can see RR Lyrae and Cepheids in relatively nearby galaxies, but they are too faint to be detected in galaxies located far, far from the Milky Way. In order to estimate the distances to those galaxies, we need to use other indicators -- which involve extra approximations and assumptions.

It's a precarious business, relying on a ladder of this sort, but this is the only way we can determine the distances to galaxies at cosmological distances; and, therefore, one of the very few ways to gain some understanding of the fundamental properties of our universe.
It all comes down to distances.
Over the years, many different astronomers have applied different distance-measuring techniques to a wide variety of galaxies, and then analyzed the results using a range of statistical methods. The result has been a healthy uncertainty in the "best" value of H0.
The astronomical community realized after World War II that Hubble's initial value of around 500 km/s/Mpc was far too large, and so the value dropped quickly. In the 1970s and 1980s, however, a gap appeared between the estimates published by groups led by two particular astronomers: Allan Sandage and Gerard de Vaucouleurs.
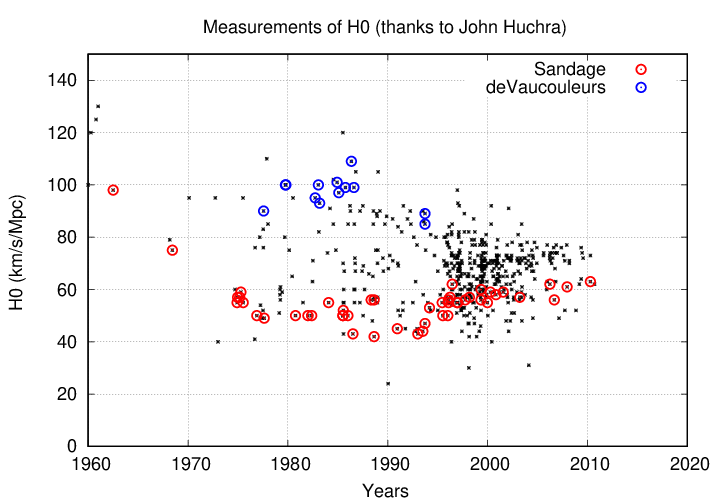
For a while, the difference was a robust factor of two -- not a very satisfactory state of affairs. I was a grad student during those days, when some people had pretty strong feelings about the two camps. It was clear that someone had to be wrong -- but who?
Fortunately, with improved technology (especially access to telescopes in space), the gap closed during the decades of the 1990s and 2000s, and most people agreed that the Hubble Constant had a value somewhere in the neighborhood of 70 km/s/Mpc. Phew.
However, in the past twenty years, a new -- though much smaller -- gap has appeared. The difference is now not so much WHO is doing the calculations, as WHAT is the basis for the work. Values computed using the traditional "distance ladder" approach are consistently running about 72 km/s/Mpc, while those based on measurements of the Cosmic Microwave Background (CMB), using a very, very different set of calculations and assumptions, yield a consistently lower value: about 67 km/s/Mpc.

Q: Do the two sets of measurements agree within the stated
uncertainties? In other words, do the errorbars overlap?
No, the errorbars do NOT overlap. Each side has checked and re-checked its work, and each side believes that its errorbars are reasonable. The result is known as Hubble tension.
What is the solution? Could there be a systematic effect lurking in our distance ladder? Is it possible that the local universe -- in which we apply the distance ladder -- has properties which differ a bit from those of the universe as a whole?
At the moment, we just don't know.
 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.