Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Remember measuring the distance to an asteroid by analyzing its apparent position in simultaneous images taken at two locations on Earth? That technique, called parallax, can also be used to measure the distances to some nearby stars ... if one modifies the observations a bit.
The simplest way to measure the distance to an object via parallax is to make simultaneous measurements from two locations on Earth. However, this method only works for objects which are relatively nearby:
Object maximum possible parallax
(arcseconds)
-------------------------------------------------
Mars 34
Jupiter 4
Neptune 0.6
Proxima Centauri 0.00007
-------------------------------------------------
The smallest angle one can measure from the ground with an optical telescope is about 0.003 arcseconds. It seems that simultaneous measurements from two locations will only work for bodies within our own solar system. We need to find some larger baseline to measure the parallax to other stars....
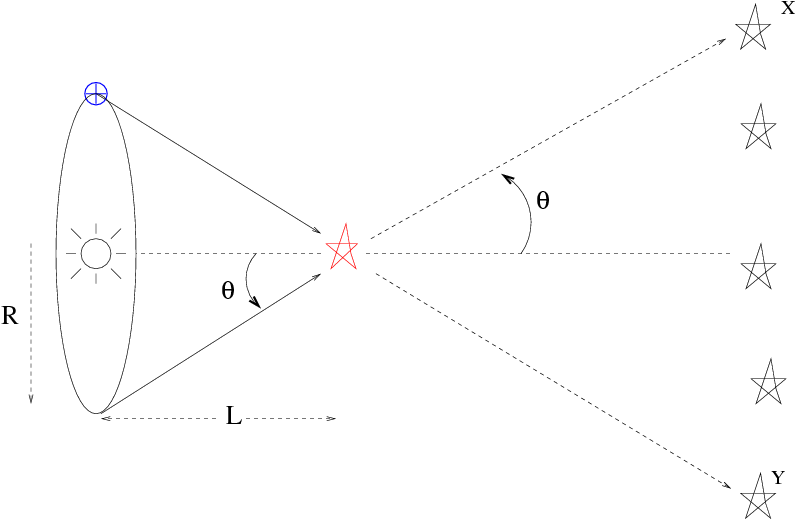
Astronomers need a VERY long baseline in order to produce a parallax angle which is large enough to detect via conventional imaging. Fortunately, there is a convenient baseline just waiting to be used -- if we are willing to discard the requirement that measurements be simultaneous (more on this later). This longer baseline is the radius of the Earth's orbit around the Sun:
Note the convention used only in this situation: the quoted "heliocentric parallax angle" θ is always HALF the apparent angular shift.
So, if we measure a parallax half-angle θ to a star, we can calculate its distance very simply:
R
L = ---------
tan(θ)
where
6
R = 149.6 x 10 km
= 1 Astronomical Unit (AU)
Now, for small angles -- and the angles are always small for stars -- we can use the small angle approximations:
tan(θ) ~= sin(θ) ~= θ
as long as we measure the angle in radians. Even if we don't
use radians, it still remains true that cutting a small angle
in half will also cut its tangent in half
θ 1
tan( --- ) ~= --- tan( θ )
2 2
and, in general, there is a linear relationship between
the tiny angle θ and its tangent, regardless of the units.
Take a look for yourself:
angle angle tan(angle)
(degrees) (radians)
--------------------------------------------
1 0.017453 0.017455
0.5 0.008727 0.008727
0.1 0.0017453 0.0017453
0.01 0.00017453 0.00017453
--------------------------------------------
Okay, fine. Why am I belaboring this point? Because astronomers have chosen a set of units for parallax calculations which look strange, but turn out to simplify the actual work. The relationships between these units depend on the fact that there is a simple linear relationship between a tiny parallax angle, in ANY units, and the tangent of that angle.
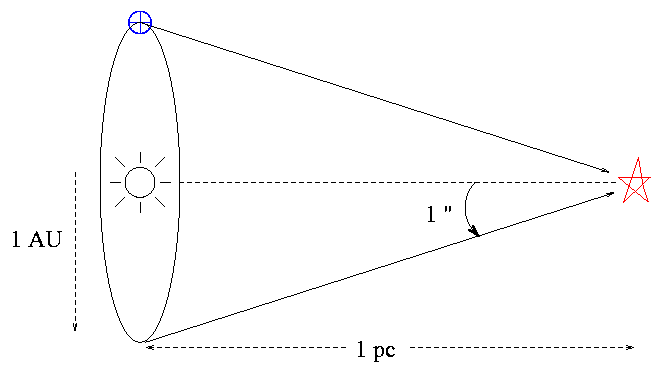
Q: How many meters are in one parsec?
How many light years are in one parsec?
Given these units, and the linear relationship between a small angle and its tangent, we can calculate the distance to a star (in pc) very simply if we know its parallax half-angle in arcseconds:
1
distance (pc) = -----
θ
Give it a try: the first star to have its parallax measured was 61 Cygni. In 1838, Friedrich Bessel calculated its parallax half-angle to be θ = 0.314 arcsec.
Q: What is the distance to 61 Cygni based on Bessel's measurement?
It sounds pretty easy to measure the distance to another star -- just make measurements of its position six months apart. In practice, however, it is very difficult. The first successful measurement of stellar parallax came more than two hundred years after the invention of the telescope. What took astronomers so long?
Really small. Smaller than the apparent size of stars as seen from the Earth's surface. Starlight is refracted by air as it passes through the Earth's atmosphere. It encounters layers with a range of temperatures and pressures, and, what's worse, all these layers are constantly in motion.
As a result of all this refraction, astronomers on the ground perceive stars to be little blurry spots. The typical size of a "seeing disk" is around 1 arcsecond. In order to measure the parallax of a star, we must determine its position -- and that of several reference stars in the same field -- to a very small fraction of this seeing disk. That's not an easy task.
In practice, astronomers usually measure the shift of one star in an image relative to other stars in the same image; differential measurements can be made much more precisely than absolute ones. However, as the Earth moves from one side of the Sun to the other, we will see ALL the stars in the field shift, not only the star of interest.
The only hope is to pick out a set of reference stars which happen to be much farther away than the target star. Distant stars will shift by a much smaller angle -- perhaps small enough to be imperceptible. If we measure the position of the nearby target star relative to those distant ones, we might be able to detect its shift.
We have to wait months for the Earth to move a significant distance in its orbit around the Sun. During that time, the Sun is moving through space at a decent clip: very roughly 12 km/s relative to nearby stars in the disk of the Milky Way. Other stars are moving, too, by similar speeds. The resulting proper motions can be signficant at the level of precision required for parallax measurements.
For example, when we look at the nearby star Vega, we might expect it to move in a simple line between two apparent positions:
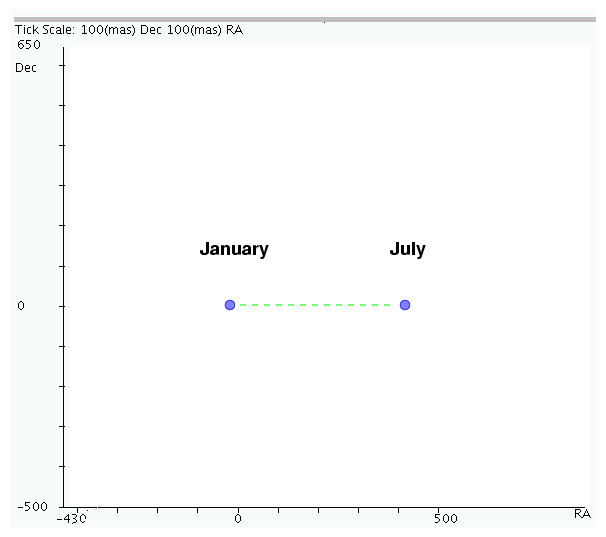
But its real motion shows the combination of parallax and proper motion. Consider these observations of Vega over a period of three years, made by the Hipparcos satellite.
Q: What is the parallax of Vega?
Q: What is the distance to Vega?
The precision of the Hipparcos measurements of parallax is about 0.002 arcsecond. That means that we can rely on Hipparcos measurements to determine distances out to 100 parsecs or a bit further.
The European Space Agency is planning to launch in 2013 the Gaia satellite, which is very much like a big brother to Hipparcos. It will also measure the positions and distances to stars, but do a better job:
Hipparcos Gaia
----------------------------------------------------------
Telescope diam (cm) 29 ~ 100
Mag limit 12 20
# stars (approx) 100,000 1,000,000,000
best precision 0.001 0.000 010
(arcsec)
velocity measures none 1-10 km/s at V=16
----------------------------------------------------------
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.