
 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Given the properties of a medium -- air, or a vacuum, or a string stretched between two posts -- we can use the wave equation to understand the properties of disturbances inside that medium.

Waves moving through the medium must satisfy this equation, and they must also satisfy any initial conditions or boundary conditions that may be imposed in some particular situation.
Finally, we know that there may be multiple solutions to this wave equation within some region. The principle of superposition states that any linear combination of solutions is also a solution. In other words, we can add together two or more waves, if necessary, in order to satisfy initial or boundary conditions.
We will use all this information to investigate the behavior of travelling waves when they meet some obstruction.
They may be reflected completely, or may pass by the obstruction, or may end up doing both: being partially reflected, and partially transmitted (as in the picture below). The answer will depend on the particular circumstances in each case.

Image courtesy of
D-Kuru and Wikipedia
The examples here will involve sinusoidal waves travelling along strings, but the results can be extended to more general cases.
Consider our old friend, the string of mass M and length L stretched under tension T between two fixed pegs, We know from lectures past that this string can oscillate in a normal mode, so that its vertical position is given by
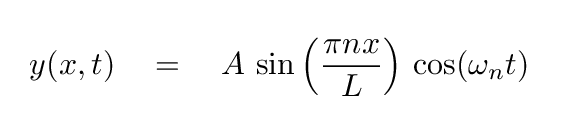
Below is an animation of one of these possible standing waves. It appears that L = 18 m.
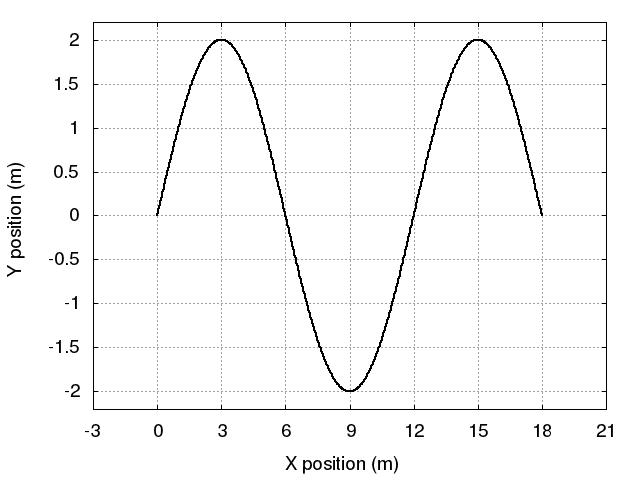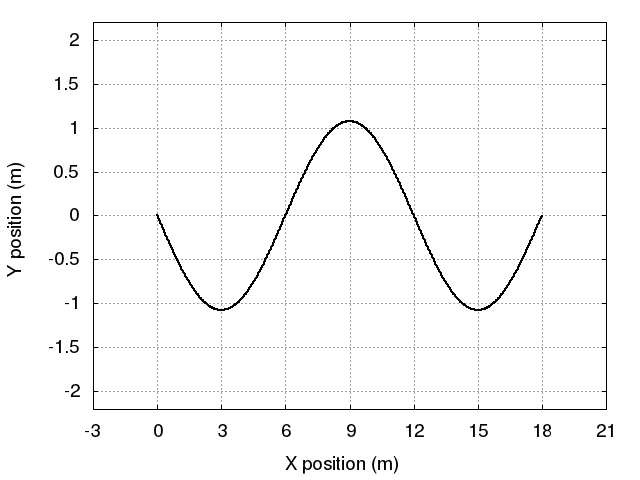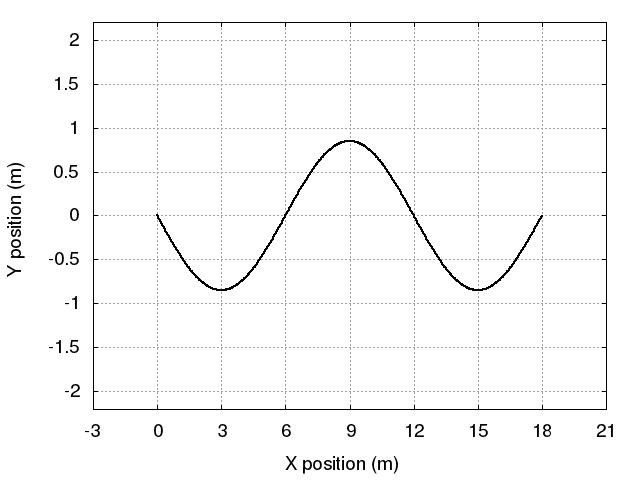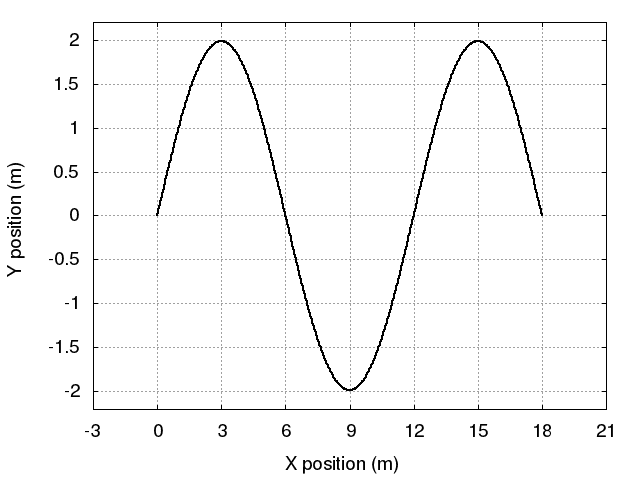
Q: What is the value of the mode n for this wave? Q: What is the value of the wavelength λ?
However, this equation is not the only way to represent this particular motion mathematically. We can also describe this standing wave as the superposition -- or interference -- of two travelling waves.

Those two travelling waves have equations
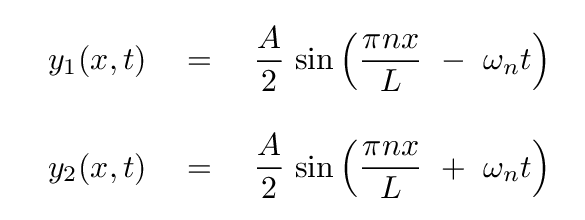
But -- wait a minute. These two equations describe vertical motions that are not observed. After all, those two equations allow one to compute a value of y for any value of x -- not only the values which lie within the range of the string.
No problem. We can simply declare that the solution to the wave equation in this particular case is split into three regions:
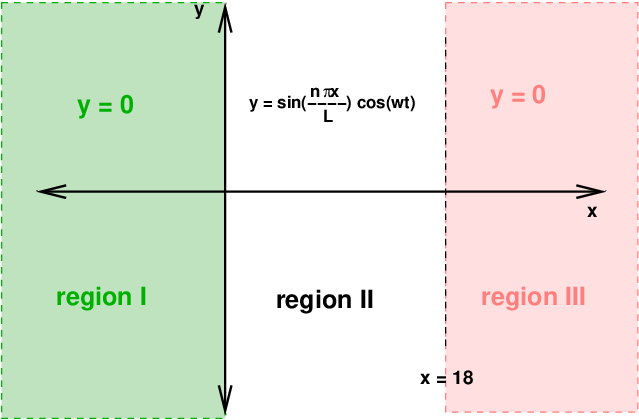
These piecewise solutions are acceptable as long as they meet a set of boundary conditions:
Well, does our proposed travelling-wave solution satisfy these boundary conditions? In this case, the boundary conditions occur where region I meets region II (at x = 0), and where region II meets region III (at x = 18 m):
region I region II region III
y = 0 y = y1(x,t) + y2(x,t) y = 0
At x = 0, the sum of y1 + y2 must be zero
(because the string is tied to a peg at x = 0)
At x = 18 m, the sum of y1 + y2 must be zero
(because the string is tied to a peg at x = 18 m)
At x = 0, the sum of vy1 + vy2 must be zero
(because the string can't move at x = 0)
At x = 18 m, the sum of vy1 + vy2 must be zero
(because the string can't move at x = 18 m)
Let's check the "position" values first.
Q: What is the y-position of the sum of the travelling waves
at x = 0 m?
Q: What is the y-position of the sum of the travelling waves
at x = 18 m?
Q: Do these y-positions match the y-positions of the
solutions in the regions to the left and right
of the string?
At x = 0 m and at x = 18 m, the two travelling waves always add up to y = 0. Since that's the same as the value of y in the neighboring regions, we've satisfied the first boundary conditions. Hooray!
Q: What is the y-velocity of the sum of the travelling waves
at x = 0 m?
Q: What is the y-velocity of the sum of the travelling waves
at x = 18 m?
Q: Do these y-velocities match the y-velocities of the
solutions in the regions to the left and right
of the string?
At x = 0 m and at x = 18 m, the y-velocities of the two travelling waves always add up to vy = 0. Since that's the same as the value of vy in the neighboring regions, we've satisfied the second set of boundary conditions. Yippee!
Since our proposed solution, consisting of
does satisfy all the boundary conditions, and each piece satisfies the wave equation, our job is done.
Let's consider a more complicated situation. Suppose that a very long string is tied to a motor at its left end, and to a fixed point on a wall at its right end. Initially, the string is at rest. But when we turn on the motor, we create a wave which travels along the string to the right. If the motor drives the end of the string in a sinusoidal manner, with angular frequency ω, then we can describe the incoming, or incident, wave, like so (note the subscript i for "incident")
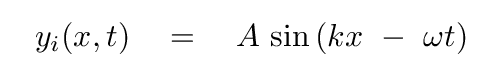
The wave number k will depend on the speed of waves travelling along the string, which, in turn, depends on the values of the tension T and mass density M/L.
The situation will look something like this as the wave approaches the wall:
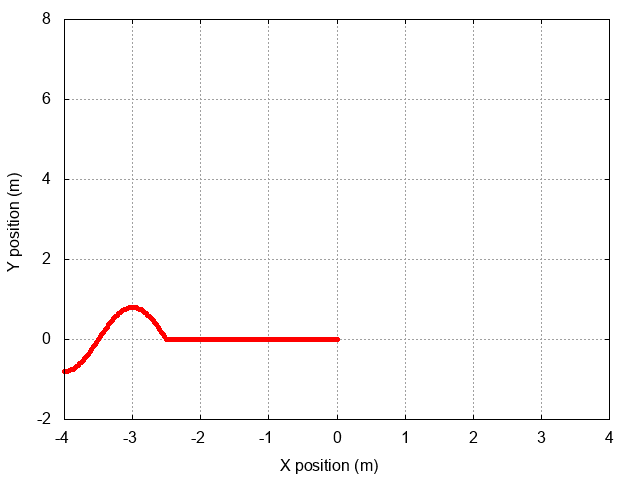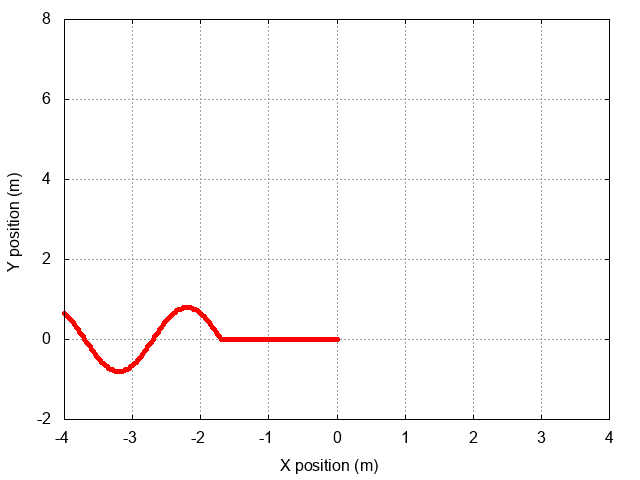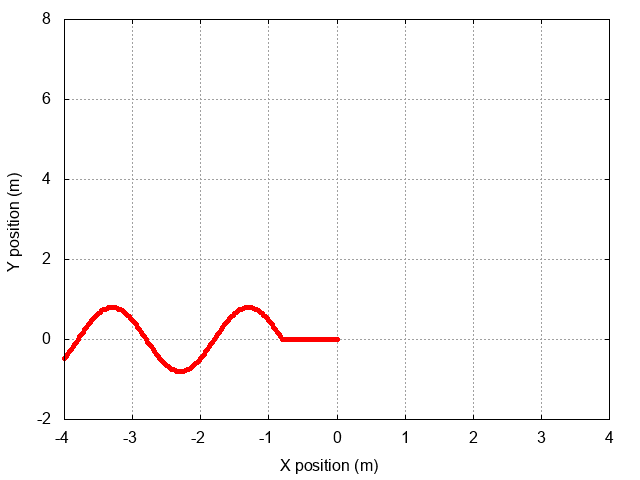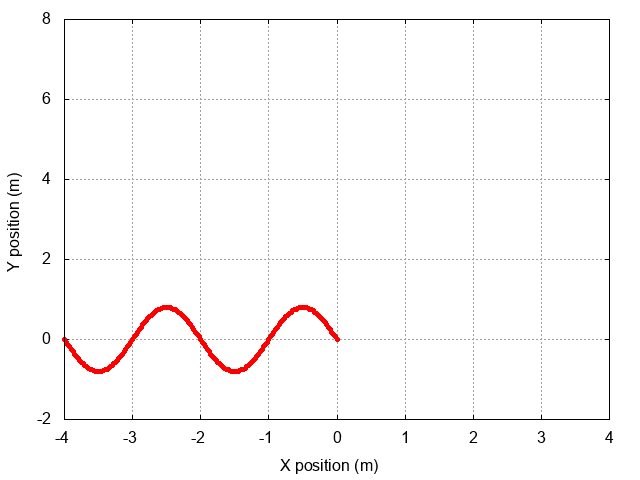
When the wave reaches the wall, some rather complicated stuff will happen. In order to make it easier to see the details, let's show just the first half-wavelength of the incoming wave.

Something is going to happen when the wave reaches the fixed end at x = 0. We might guess that a new, "reflected" wave will start moving along the string in the opposite direction, to the left.
But exactly what sort of reflected wave will appear? It might look like the incident wave:

It might look like a "negative" version of the incident wave:
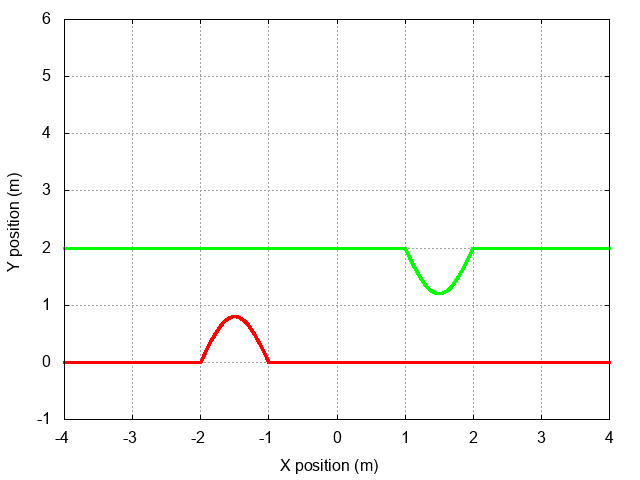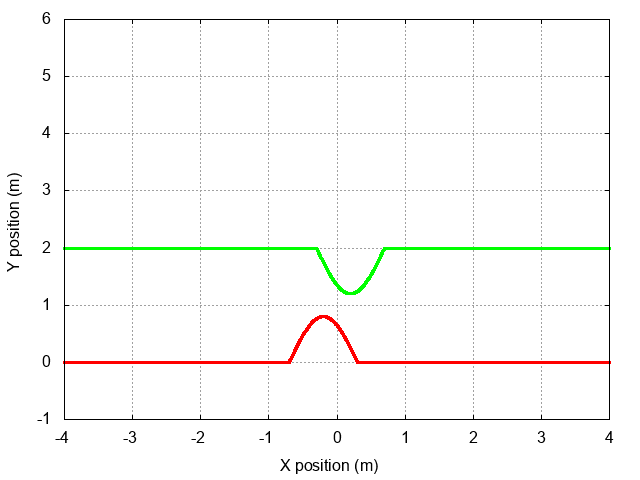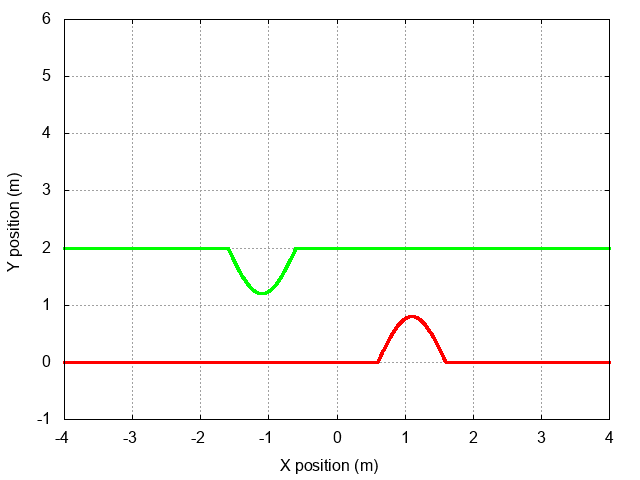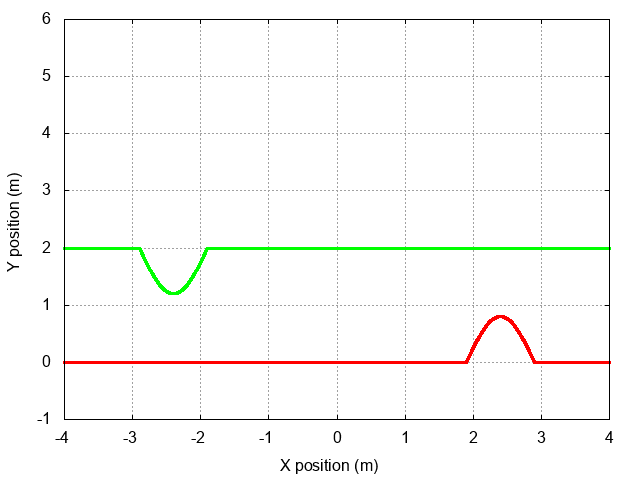
Or it might look like something else. Which of these possibilities -- if any -- matches the actual behavior of a wave on a string?
Well, we can go back to the wave equation to get started. Given the properties of the string and the motor listed earlier, and our knowledge of solutions to the wave equation,
Q: How many non-zero solutions to this equation are there? Q: What are they?
I think one can list four possible, non-zero, solutions to the wave moving along the string:
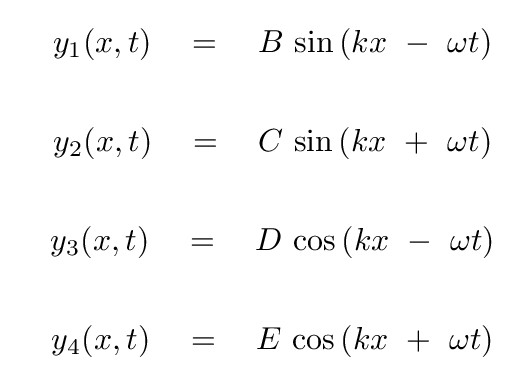
Two of these, y1 and y3, represent waves moving to the right, so they aren't going to help us with the reflected wave. However, under some circumstances, a portion of the incident wave reaching some boundary may pass through it, leading to a transmitted component; in such a case, we would look to y1 and y3 to build the transmitted wave.
So, we are left with two possible equations to represent the reflected wave. The boundary conditions in this particular case state
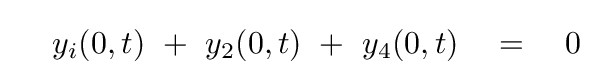
or, in other words,
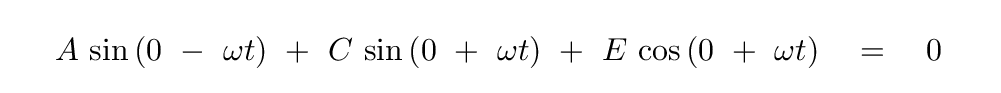
Q: What are the constraints on the coefficients C and E?
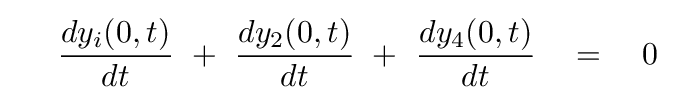
Q: Replace the derivatives above with expressions based
on the incident and reflected waves
Q: What are the constraints on the coefficients C and E?
Putting it all together, we find that the equation of the reflected (yr) wave must look like
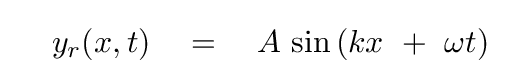
It may not look like it, but this equation for the reflected wave yields a wave which is INVERTED --- at the special boundary location x = 0 -- relative to the incident wave.
And so when the incident wave (in red) reaches the end of the string, the reflected wave (in green) must have an INVERTED displacement, but the same wavelength and angular frequency and speed, as the incident one. Note the somewhat strange shape of the sum of the two (in blue) during the first few moments after the incident wave reaches the end of the string. But also note that this sum is always exactly zero at the endpoint.
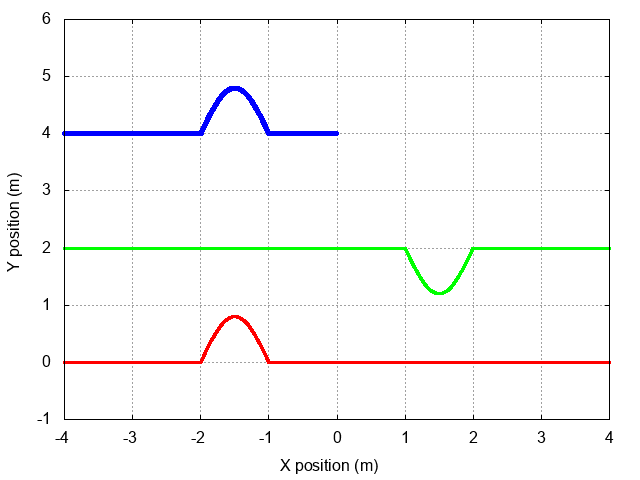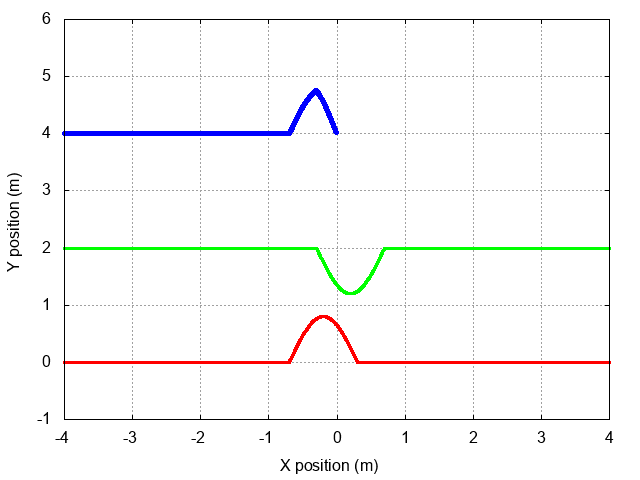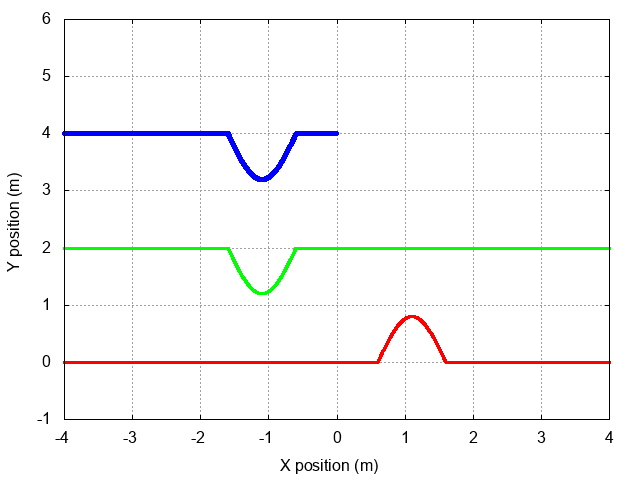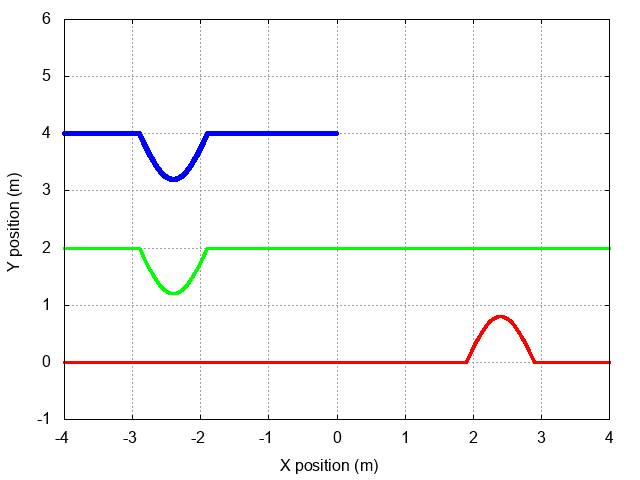
Things are bit more complicated if we show the full incident and reflected waves, but if you watch the animation below several times, it should start to make sense. Focus on the black box centered on x = 0 to see that the incident and reflected waves always add up to zero at that location.

The uppermost region of the graph shows the sum of the incident and reflected waves on the string. The sum is simply a standing wave that propagates back along the string, away from the wall.
The title says it all. Do real waves running down a string produce INVERTED versions of themselves when they reach a fixed end of the string?
Thanks to the people at School of Physics, UNSW, in Sydney, Australia, we can find out. (Click on the image to show the movie)

Image and movie courtesy of
School of Physics, UNSW, in Sydney, Australia,
Here's a closeup of the moment when the wave first reaches the fixed end of the string. Note the correspondence of theory and experiment. (Click on the image to show the movie)
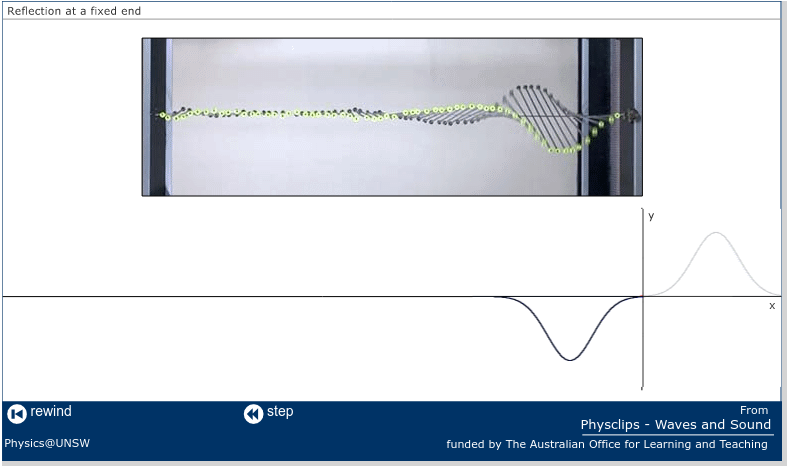
Image and movie courtesy of
School of Physics, UNSW, in Sydney, Australia,
So, yes, real waves do agree with theory.
The string in our example has been tied to a fixed post at its right end, at x = 0. That means that the vertical motion (and velocity) of the string at that point must be zero.
But we can also arrange a string which is free to move. We could, for example, tie the end of the string to a ring which can slide without friction along a post.

If the end of the string starts to move vertically, the ring allows it to continue moving, just as if it were free.

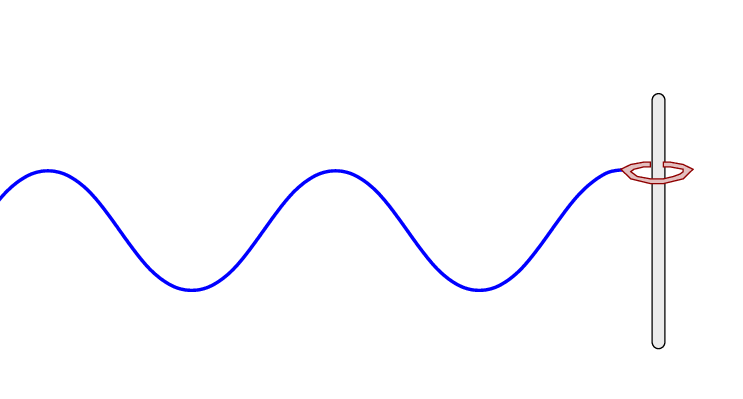
We might call this boundary condition an "free" one, as opposed to the "fixed" end we considered earlier.
What will happen when the travelling wave reaches this "free" end of the string at x = 0?
Once again, if the reflected wave travels back along the string in the negative-x direction, then only two of the four possible waves
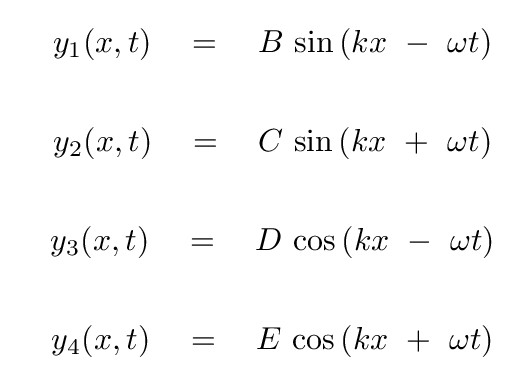
are relevant: y2 and y4.
The boundary condition this time is different: the y position of the string at the boundary is NOT fixed at zero. Instead, the end of the string can move up and down over some range.
Finding the proper boundary condition for this case is a bit difficult. I don't have time to go into the details here, but it is possible to show that in this case, the proper conditions are
1: the y-position of the incident wave is equal to the y-position
of the reflected wave
2: the vy velocity of the incident wave is equal to the vy velocity
of the reflected wave
These two conditions can be stated in other ways; for example, they are equivalent to "the net vertical force on the free end of the string must be zero," or "the slope of the string at the free end must always be zero." Again, it's a bit complicated to explain, so let's just focus on the results: the two conditions listed above.
If you apply those conditions to our incident (yi) and reflected (y2 and y4) travelling wave candidates,
Q: What constraints do these place on coefficients C and E?
We find that the reflected wave must have the equation

Once again, this may not look like it, but this equation for the reflected wave means that -- at the special boundary location x = 0 -- it has the same y-position as the incident wave.
Thus, when the end of the string is free to move, it reaches a maximum amplitude twice that of the incident wave, but the reflected wave itself has the same amplitude.
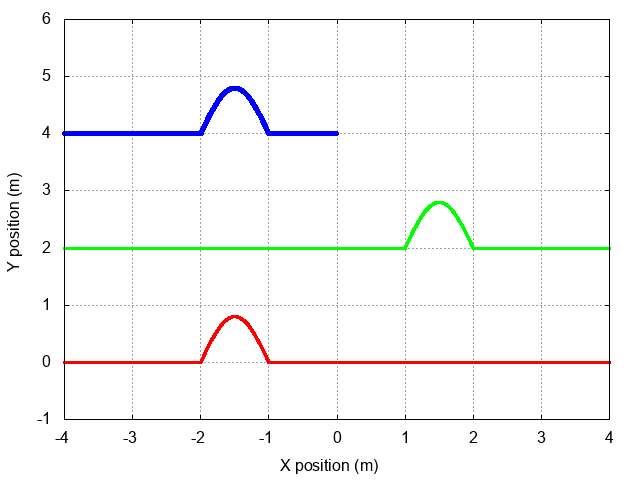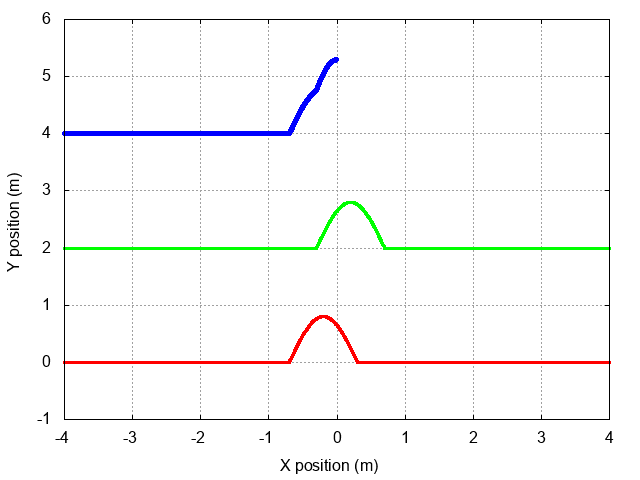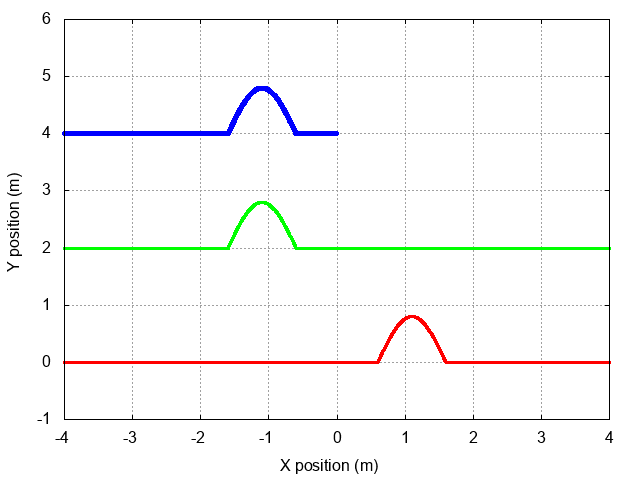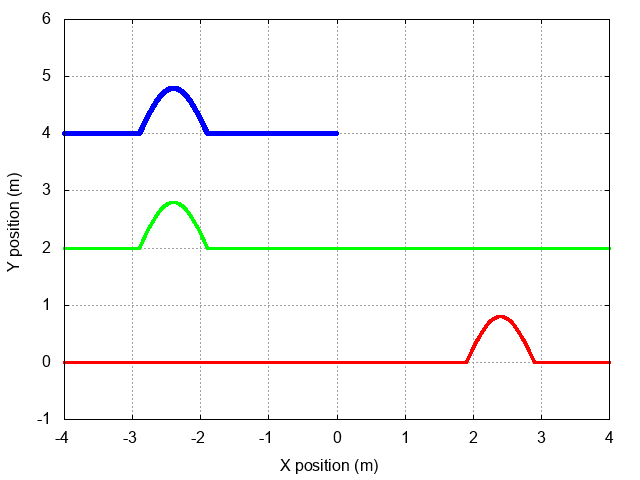
Here's a view showing the full incident and reflected waves, as well as their sum. Note that the two waves are always in phase when they meet, which causes the amplitude of the sum to be twice as large as either wave.

Once again, we can ask "Do real waves travelling towards the end of a string behave this way?" Once again, the School of Physics, UNSW, in Sydney, Australia, provides the answer.

Image and movie courtesy of
School of Physics, UNSW, in Sydney, Australia,
Here's a closeup of the moment when the wave first reaches the free end of the string.
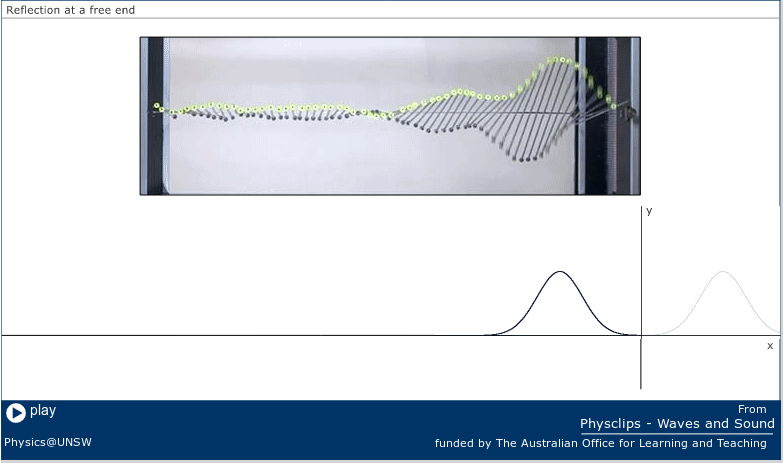
Image and movie courtesy of
School of Physics, UNSW, in Sydney, Australia,
We can summarize the results as follows:
 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.