Investigating planets around other stars

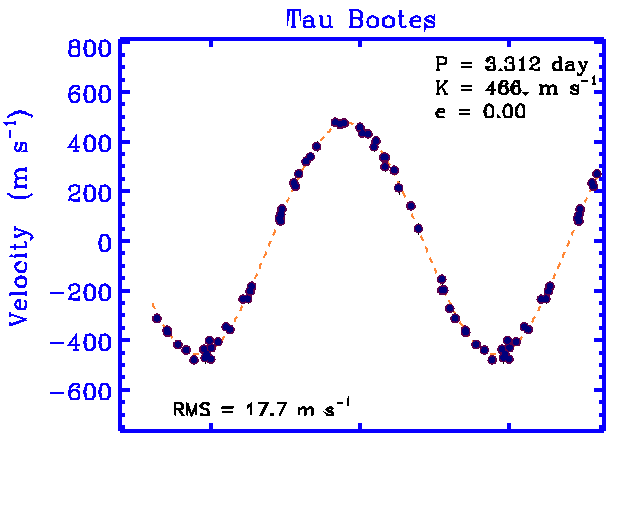
Look at the measurements of a star called "tau Bootes". This star moves in a circle with a period of P = 3.312 days and a speed of about v = 466 m/s.

1. What is the circumference of the star's orbit? In other words, how far does the star travel as it makes one complete circle?
2. What is the radius R_s of the star's orbit around the center of mass?
3. The planet is circling the star with a much larger orbital radius R_p, but with exactly the same period P. Use Kepler's Third Law to figure out the radius of the planet's orbit. You can assume that
   • (R_p + R_s) is roughly (R_p)
   • the mass of the star is about the same as the mass of the Sun
4. How does the planet's orbit compare in size of the orbit of the Earth around the Sun?
5. Use the ratio of orbital radii to figure out the ratio of masses. Then estimate the mass of the planet.
6. How does the planet's mass compare to the mass of the Earth?
7. Would you like to live on this planet?

For more information

• Different methods for finding extrasolar planets from an introductory astronomy course.
• A few thoughts on life on the known extra-solar planets, ditto
• The extrasolar planets encyclopedia has up-to-date information. The US mirror site may be faster.

Copyright © Michael Richmond. This work is licensed under a Creative Commons License.