Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
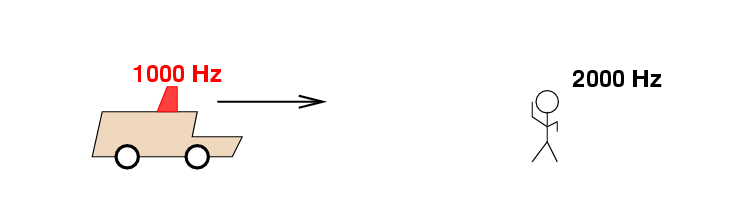
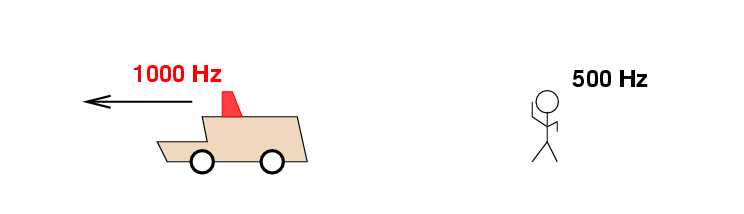
You may be familiar with the Doppler effect: a change in the perceived frequency of a sound due to motion of the source or the observer.
The basic idea is that
The ordinary Doppler effect occurs to waves which run through a medium; in most examples, we consider sound waves travelling through the air. Light waves, however, do not require a medium: they can travel through empty space. There is still a Doppler effect for light -- and it still has the same general form, with converging motion leading to higher frequencies -- but the rules are a little different. Let's take a closer look.
There is no change to the frequency of sound waves if the sources moves across the observer's line of sight. However, that is not true for light waves. The reason is pretty simple: clocks on the moving source don't run at the same rate as clocks on the observer.
It will help to review a few properties of waves first. The speed of a wave is given by the product of its frequency and its wavelength.
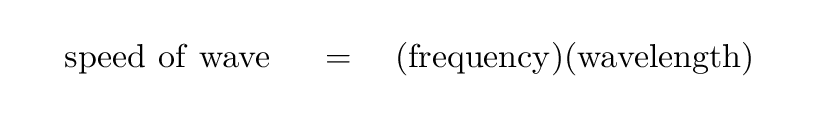
The common symbols used here are
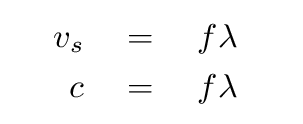
The frequency of a wave is just the number of crests which pass the observer each second. If we use the symbol T to mean "the time between successive crests", then we can write:
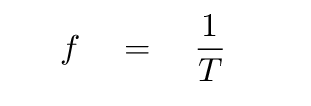
Now, suppose that a car has a lamp on the top which emits light of a certain frequency f, measured in the car's own reference frame.
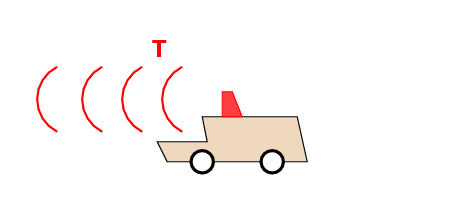
The time between successive crests of the light, in the car's reference frame, is
Suppose that the car drives past Fred at a high speed v, moving across his line of sight:
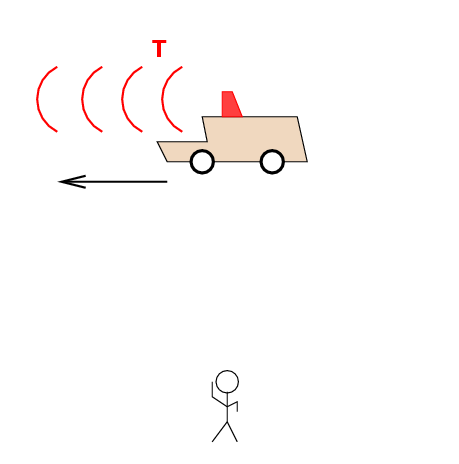
According to Fred, clocks on the car are ticking slowly. Not only do clocks run slowly, but all physical processes on the car occur slowly. The time dilation factor gamma relates the rate at which clocks on the car run relative to Fred's clocks:
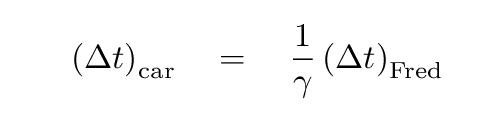
This dilation applies to the duration between two successive wave crests emitted by the lamp.
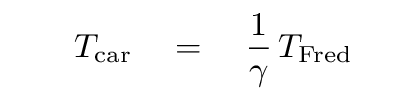
And so we can easily calculate the frequency measured by Fred if we know the frequency emitted by the lamp and the gamma factor for the car.
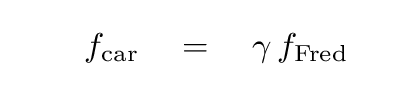
Or, in more general terms, the frequency of light emitted by some source, and the frequency of light measured by an observer, will be
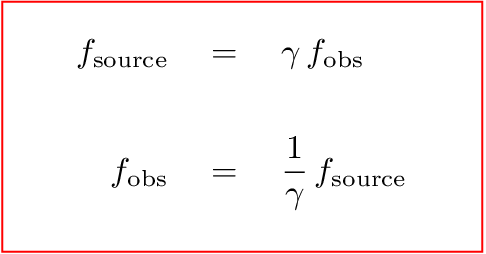
Q: Joe has an ordinary red laser pointer which
emits red light, with a wavelength of
about 650 nm. He points the laser directly
up into the night sky.
Aliens flying past the Earth at v = 0.9c
look straight down at Joe and his laser.
What wavelength do they measure?
Can their captive human servants see this light?
Q: The Earth orbits the Sun at a distance
of about R = 1.5 x 10^(11) m.
If the Sun emits light with wavelength
650.0 nm, what is the wavelength measured
by astronomers on Earth?
Let's now consider the case in which a light source moves directly towards or away from the observer. We'll begin with a lamp, which emits light waves with a frequency f. Each crest of the wave comes out of the lamp a time T = 1/f after the previous crest. The distance between successive crests is therefore cT.
It will help to have a little coordinate axis which shows the location of each crest of the wave, as measured by observers in the frame of the lamp. I've labelled 5 particular crests of the light wave, marked at time t = 0.
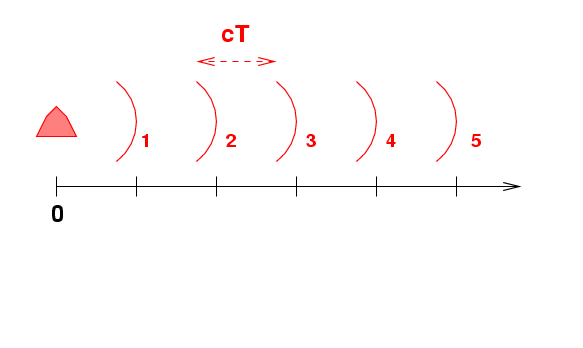
Of course, each crest moves to the right with speed c. We can write an equation which yields the position of any particular wave crest as a function of time t like so:
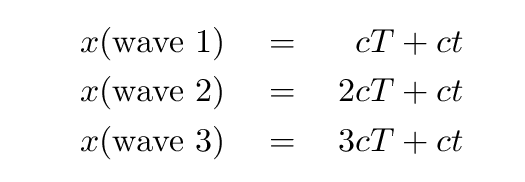
Now, let's add an observer. He sits inside a car which drives to the right at speed v. At time t = 0, when we start watching carefully, the car is already some distance away from the lamp, at x = L.
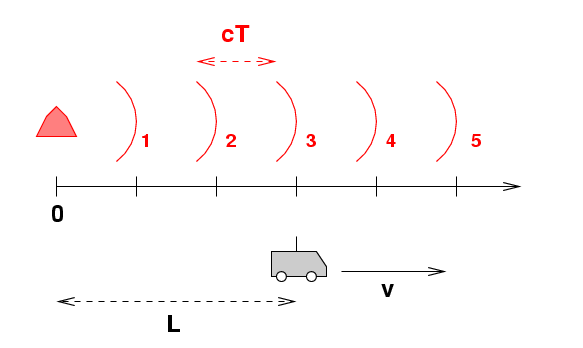
It's not too hard to write an equation which yields the position of the car at any time, in the frame of the lamp.
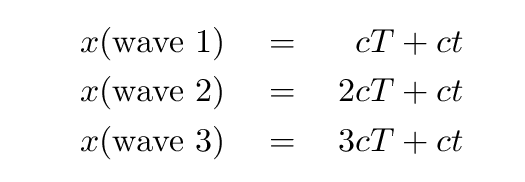
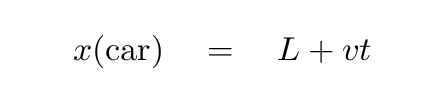
As time goes on, the car will drive to the right, but light waves from the lamp will overtake the car and pass it. Let's define two specific events:
Can you figure out when and where these two events will occur, according to observers in the frame of the lamp?
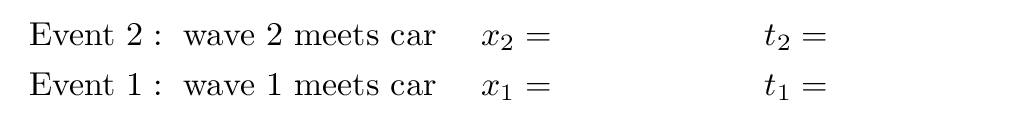
The time difference between these two events is the interval between two successive wave crests passing the car. If we can determine this interval as measured by the people in the car, then we can calculate the frequency of light they perceive.
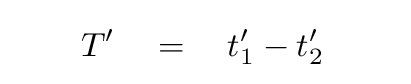
So, your job is to start with the coordinates of events 1 and 2 in the frame of the lamp, and transform them into the coordinates in the frame of the car.
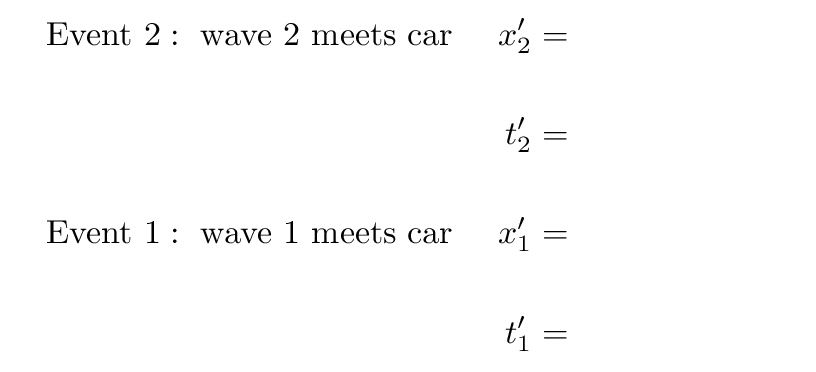
Fine. Now, compute the time interval between the two events as measured by observers in the car. Yes, it will look big and long and ugly, but it can be simplified if you take your time .... It helps if, at the right moment, you replace factors of v/c with the symbol β.
Okay! If you know the time interval T' between successive wave crests (as measured by people in the car), you can calculate the frequency f' they measure.
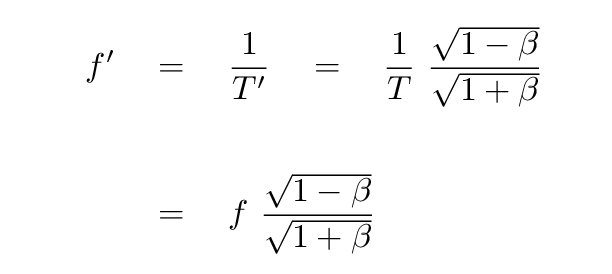
So, in general terms,
Q: Your favorite radio station is WXXI-AM,
which broadcasts at a frequency f = 1370 kHz.
As your superjet flies away from Rochester
at v = 0.5c, where must you tune your
radio dial to hear the station?
In everyday circumstances, observers don't move past each other at half the speed of light; in fact, relative speeds are never even one percent of the speed of light. The ratio of the velocity of the moving reference frame v to the speed of light c is always very, very small.
Under those circumstances, you can use the binomial expansion TWICE to simplify the Doppler formula so that it looks something like this
with a single factor of v/c inside the parantheses. Can you do it?
The result should be
Q: Your favorite radio station is WXXI-AM,
which broadcasts at a frequency f = 1370 kHz.
As your ordinary automobile drives away from Rochester
at v = 30 m/s, where must you tune your
radio dial to hear the station?
The Kepler satellite is designed to make VERY precise measurements of the brightness of stars. A recent paper by Bloeman et al. describes how this satellite was able to detect the relativistic Doppler shift in a binary star system. The two stars are orbiting each other so that they eclipse one another from our point of view on Earth. Kepler's camera easily detects the deep, short variations in brightness due to the eclipses, as well as the gradual change in brightness due to the ellipsoidal shape of one of the stars.
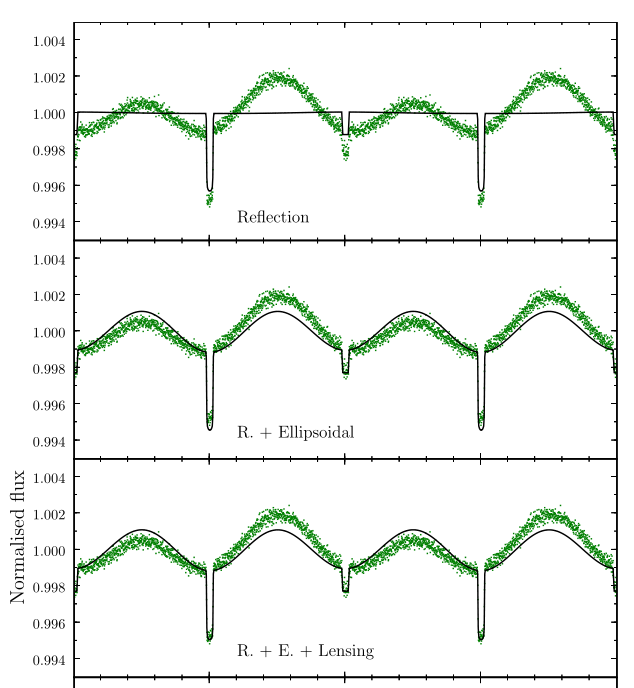
However, even after adding other physical effects to their model, the astronomers could not make their model match the observed light curve. What other effect could be acting?
The Doppler effect, of course!
One of the stars (shown in blue below) is larger and hotter than its companion, so it provides most of the light.
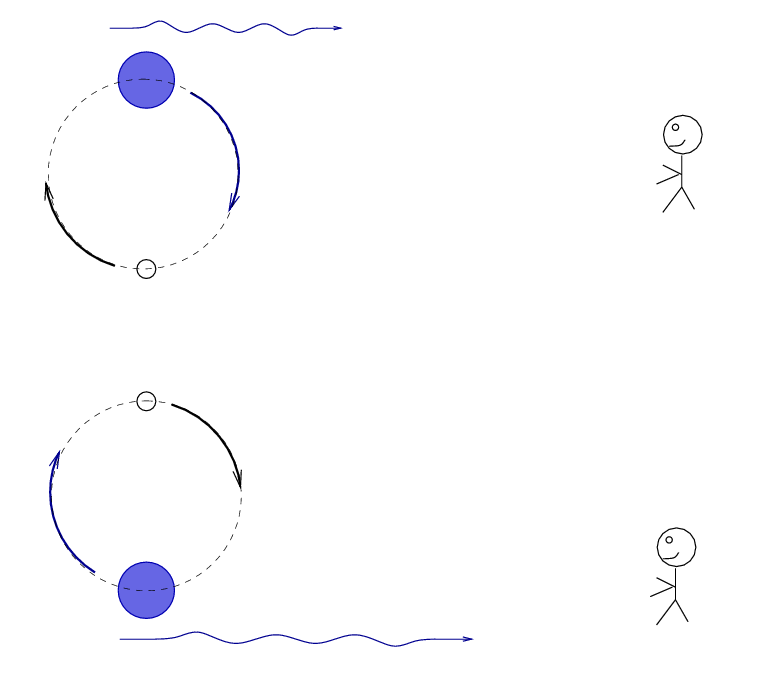
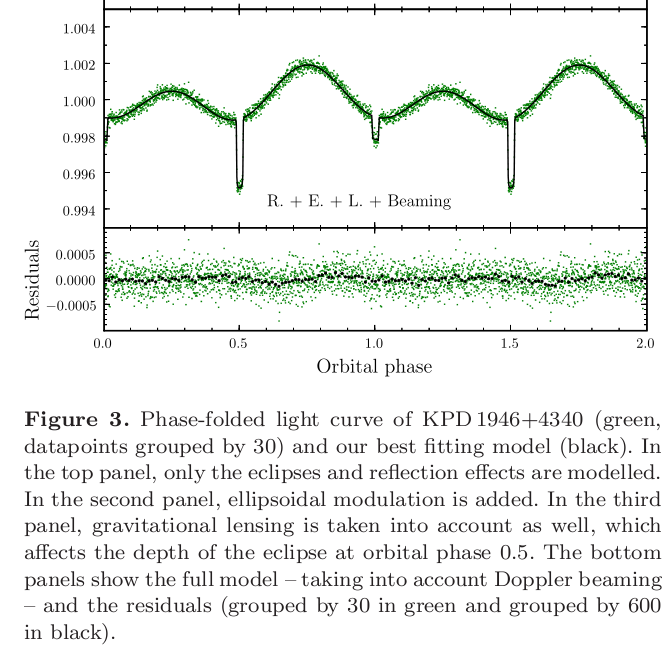
When the blue star is moving towards us, the photons it emits are blueshifted (and beamed, another relativistic effect we have not discussed). The net effect is that the apparent brightness of the star increases slightly. When the blue star is moving away from us, the photons it emits are redshift (and de-beamed), with the result that the apparent brightness drops slightly. When Bloemen et al. computed the Doppler shifting (and beaming) effects and added them to their model, they found an excellent match to the measurements.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.