Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
You're all familiar with the Doppler effect, right? Waves of any sort -- sound waves, light waves, water waves -- emitted at some frequency by a moving object are perceived at a different frequency by a stationary observer.
When source and observer are stationary, observer sees waves of frequency ν or wavelength λ.
But if the source moves towards the observer, then the perceived frequency ν' is higher than the emitted frequency, and the perceived wavelength λ' is shorter than the emitted wavelength.
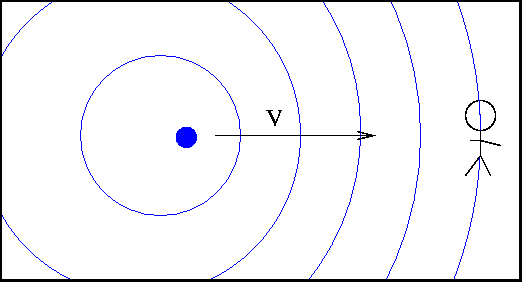
One can derive equations which connect the emitted and observed frequencies and wavelengths, in the ordinary, everyday regime:
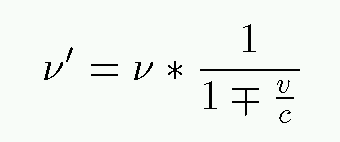
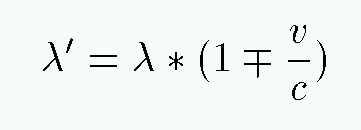
where one uses the top sign if the source is approaching, and the minus sign if the source is receding from the observer. There are similar equations which describe the change in frequency and wavelength if the observer is moving.
Please note two things about this classical Doppler effect.
If you accept the postulates of Einstein's Theory of Special Relativity, you can derive a somewhat different relationship between frequency (or wavelength) and motion. One simple way to see it is to note that the clock on a moving source runs slow by a factor of γ, so that it appears (to a stationary observer) to take the source a bit longer to create each wave crest. Thus, the rate at which new wave crests appear -- the frequency -- is slowed down by γ.
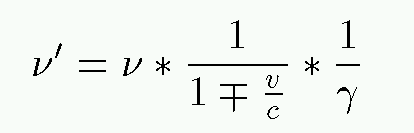
One can do a little algebra and re-write this in a pleasingly symmetric form:
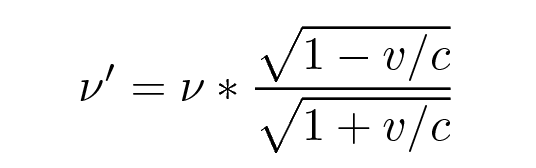
as long as we define the velocity v to be
Likewise, one can express the shifted wavelength λ as
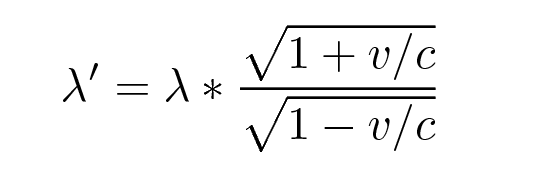
Just how big is the difference between the ordinary Doppler shift and the relativistic Doppler shift? Let's find out ...
Q: A source emits light at wavelength λ = 480 nm.
If the source comes towards you at v = 100 m/s,
what is the perceived wavelength, according to the
ordinary Doppler formula?
Q: What is the perceived wavelength, according to the
relativistic Doppler formula?
Clearly, it's not easy to detect the relativistic effects. Scientists tried and failed many times in the years after Einstein's theory was published. In 1938, a pair of physicists at Bell Labs gave it another try:
Their scheme was clever: they designed their experiment so that even the very tiny difference between ordinary and relativistic Doppler effects would cause a perceptible change. They built a glass tube which created ionized hydrogen atoms by passing a high-voltage spark through hydrogen gas.
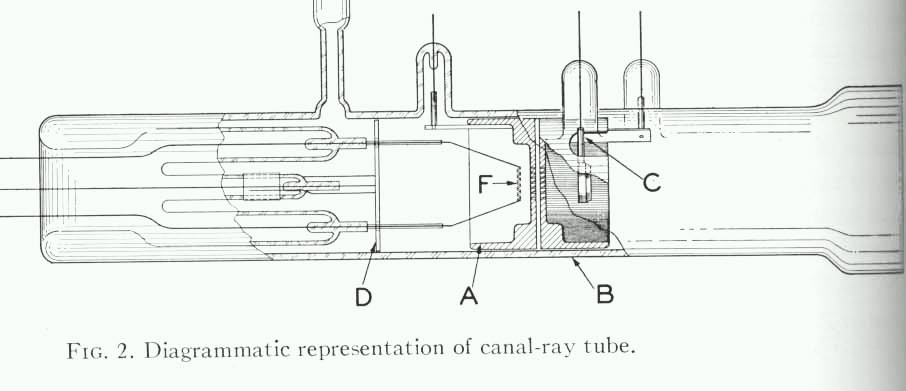
The basic idea is that hydrogen atoms are ionized by the spark between electrodes F and A. The positively charged ions are accelerated towards the negative electrode B by a strong electric field set by the voltage V between electrodes A and B.
Q: Some of the ions have mass m = 3.34E-27 kg.
If the voltage between the electrodes
is V = 10,000 volts, how fast are
the ions travelling as they shoot towards
the right end of the tube?
As the ions fly through the tube, some of them combine with electrons in the gas and radiate light with a very specific wavelength: λ = 486.009 nm = 4860.09 Angstroms. The emitted light rays fly in all directions:
Some of these rays shoot directly out to the right, out the far end of the tube and towards a spectrograph. Because these rays are emitted in the same direction as the source (atom) is moving, they will be blue-shifted to shorter wavelengths. Other rays are emitted "backwards", to the left, opposite to the direction of motion. These rays will be red-shifted to longer wavelengths. Some of the red-shifted rays strike the mirror C inside the tube and are reflected back to the right, into the spectrograph.
Now, if Einstein is wrong, and there are no corrections to the ordinary Doppler effect, the spectrograph will record two wavelengths of light: one for the direct rays, and one for the reflected rays.
Using the parameters mentioned above -- voltage V = 10,000 volts and mass m = 3.34E-27 kg -- calculate
Q: What is the predicted wavelength for the direct
rays of light?
What is the predicted wavelength for the reflected
rays of light?
What is the size of the non-relativistic Doppler
shift? That is, how many nm is the shift from rest?
On the other hand, if there IS a relativistic correction to the Doppler effect, the observed wavelengths should become
Note that now there's a second term in the expression, one which predicts a small increase in wavelength for both the direct and reflected rays.
Q: How big is the second ("relativistic") term in these
expressions?
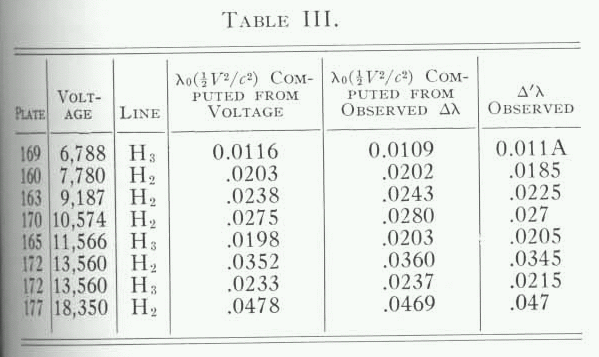
Ives and Stilwell chose a range of voltage settings V between 6,700 and 18,400 volts. They exposed photographic plates in the spectrograph to the light coming from the canal-ray tube, and measured VERY carefully the wavelengths on the plates. Below is the table of results from their paper, in which they quote wavelengths in units of Angstroms; recall that 1 nm = 10 Angstroms. Note in particular the rows for lines labelled "H2", which correspond to ions with the same mass m = 3.34E-27 kg you have been using. The second column shows the acclerating voltage, and the final column the observed extra shift (in Angstroms) after the ordinary Doppler shift was been removed.
In the classical world, an source of waves must be moving towards you or away from you in order for you to perceive a shift in the frequency (or wavelength) of its waves. If you look at an object moving exactly across your line of sight -- transversely -- then you see exactly the same frequency as the source emits.
But in the relativistic world, that's not true. Again, consider the situation if the source is moving, and observer sits still on the detector.
The magnitude of this "transverse Doppler shift" should depend simply on γ. In the equations below, the source is moving relative to a stationary detector.
It's even harder to detect this than the shift in wavelength from a source moving directly towards or away from you. In fact, it wasn't until 1963 that it was seen clearly in the laboratory:
The method was in theory simple: place a source of gamma rays on the axis of a centrifuge, and an absorber out on the edge.
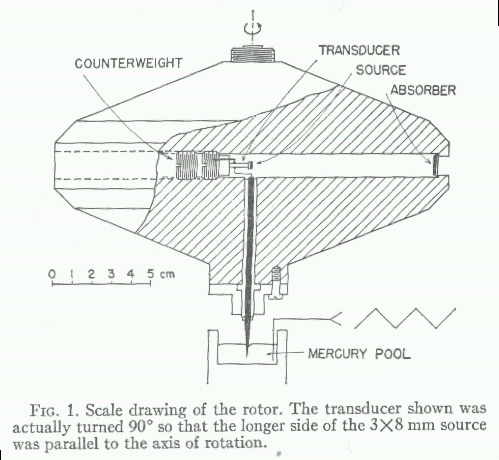
First, leave the centrifuge motionless and use the absorber to measure the frequency of the gamma rays precisely. Then, spin the centrifuge really, really fast. The detector will be moving across the line of the sight of the gamma rays as they fly outwards; or, equivalently, the source will be moving across the light of sight of the detector. Measure the frequency of the gamma rays again.
In this experiment, the radius of the centrifuge was R = 93.07 mm. In one trial, the centrifuge was spun at 35,000 rpm.
Q: What was the speed of the absorber?
By what fraction should the frequency of the
gamma rays have changed?
Believe it or not, the experiment was able to determine that the actual shift in frequency was within 1 percent of the relativistic prediction!
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.