 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Detecting gamma rays with Cerenkov light
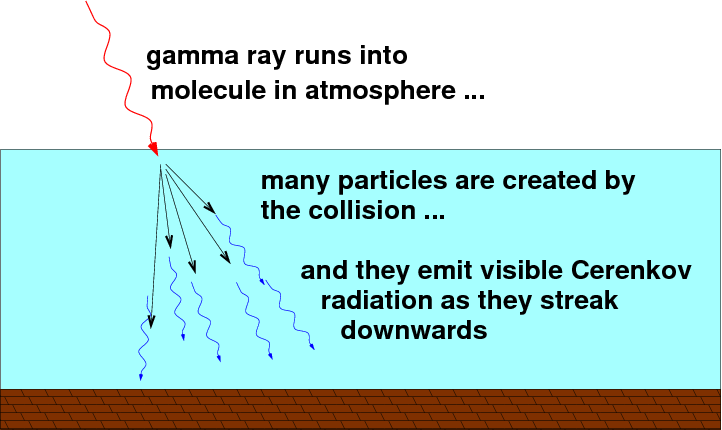
Gamma rays (and their relatives in the X-ray and UV regimes) cannot be observed directly from the ground. After travelling for millions or billions of years through the empty reaches of space, when they reach the Earth's atmosphere, they quickly collide with atoms and molecules -- BAM! Bye-bye, gamma ray.
But this collision, while it does destroy the original gamma-ray photon, can actually help us to detect it. If the gamma ray has a high enough energy, the collision will generate a large number of subatomic particles, all of which fly forward in the same direction as the gamma ray: an air shower. And if the gamma ray has a REALLY high energy, these secondary particles will move so fast through the atmosphere that they create Cerenkov light.

This clever idea turns the blanket of the atmosphere from a drawback to an advantage. In fact, this method provides a big advantage for detecting gamma rays with the highest energy. They are so rare that a "direct" sensor, like those aboard satellites in space, would have to wait a long, long time to be struck by one.
Consider these two gamma-ray telescopes:
Q: The Crab pulsar, one of the brightest sources in the sky,
has a flux at energies above 400 GeV of about
flux F = 5 x 10-7 photons per sec per sq. m.
How many photons would VERITAS collect in one hour?
How many photons would LAT collect in one hour?
So that's the good news. The bad news is that only photons with very high energies can create a large enough cloud of particles, all travelling at relativistic speeds, to appear in these atmospheric detectors. At lower energies, contamination by air showers from cosmic rays (charged particles, such as protons and electrons) limits the use of these telescopes.
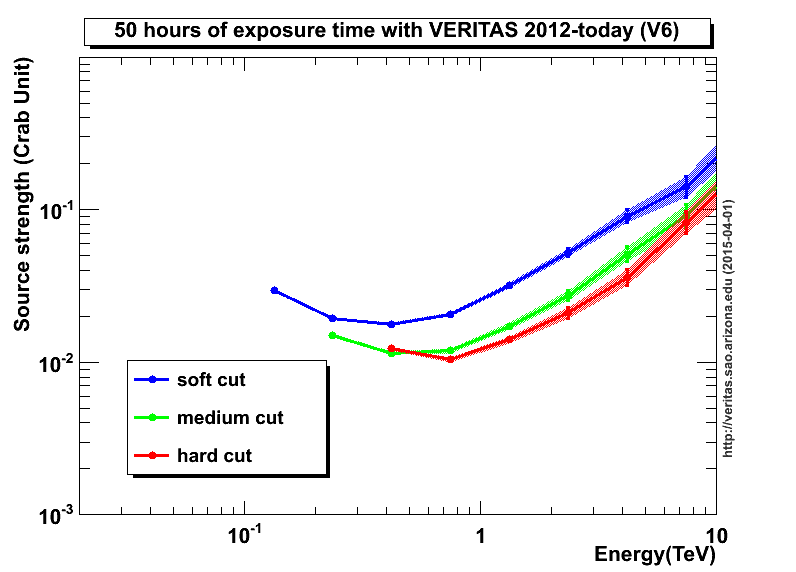
Image courtesy of
the VERITAS Collaboration
If you look closely at the mirrors of these telescopes, you'll see that most of them consist of mosaics of relatively small mirror segments. VERITAS, for example, combines 350 identical mirrors, each in the shape of a hexagon, but with simple spherical curvature, to create a roughly 12-meter light-collection system.

Image of VERITAS mirror courtesy of
VERITAS Collaboration
MAGIC's primary is 17 meters in diameter, made up of 236 segments.

Image courtesy of
ETH Institute for Particle Physics
These segmented mirrors are cheap and lightweight, making them much, much cheaper than a conventional monolithic optical mirror. These "light buckets" don't provide great image quality, of course. VERITAS has an angular resolution of about 0.1 degree, while MAGIC may do a little better: perhaps 0.05 degree.
But that's good enough. The sensors placed at the foci of these Cerenkov-light telescopes are not CCDs or CMOS arrays, but groups of photomultiplier tubes (PMTs). VERITAS, for example, has 499 PMTs packed into a square box, producing a "camera" with "pixels" about 0.15 degrees apart and a field of view of about 3.5 degrees.

Image of VERITAS light cones over a portion of the PMT array
courtesy of
the VERITAS Collaboration
Q: Why not use a CCD or CMOS sensor?
The answer is that these telescopes need to record the time of arrival of the burst of blue light from each air shower to a very high precision: about 2 or 3 nanoseconds. Why bother? Because if multiple telescopes (or other detectors) are working together to monitor some region of the sky, the time of arrival of individual photons can help the analysis in two ways:
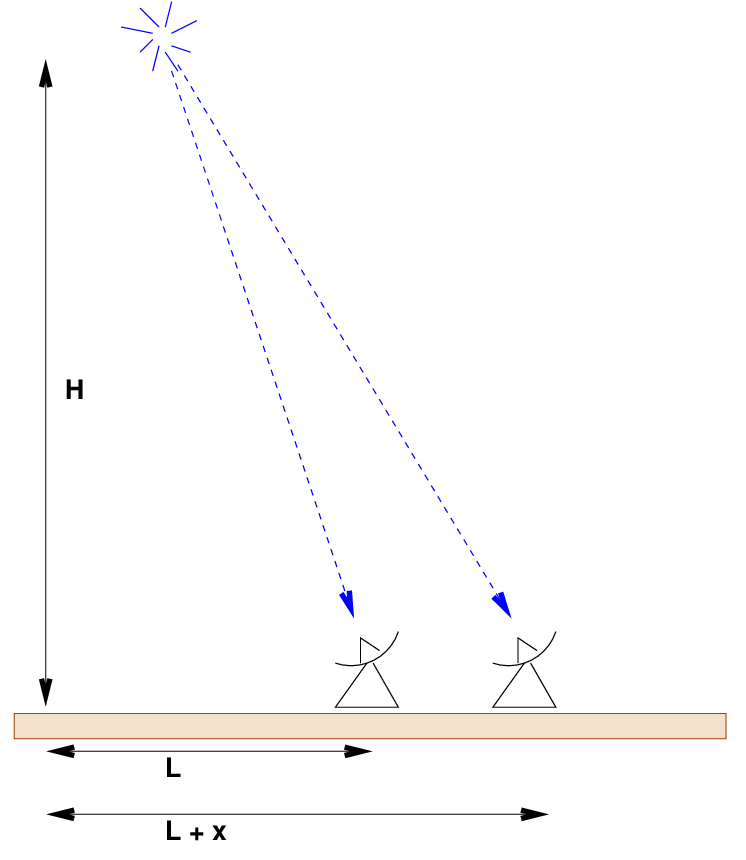
Let's see how this works. Consider a simple example, shown above. A gamma-ray smashes into a molecule at an altitude of H = 10 km. The subsequent Cerenkov radiation is detected by two telescopes on the ground, situated at horizontal distances L = 1 km and L + x = 1 km + 100 m away from the collision.
Q: How long does it take for photons from the collision
to reach the left-hand telescope?
Q: How long does it take for photons from the collision
to reach the right-hand telescope?
Q: What is the time difference in arrival times?
These time differences will be similar, and relevant, when we discuss other types of air-shower detectors in just a bit. The detectors must have very high time resolution in order to group hits together into showers, and to help provide some direction to the incoming photon.
As mentioned above, the field of view of these Cerenkov telescopes is pretty small: 3.5 degrees across for VERITAS, maybe 2 degrees for MAGIC. Astronomers must use these instruments in "pointed mode:" one must pick a target, point the telescopes at it, and track it while collecting data. It would be very difficult to make an all-sky map of the gamma-ray sky with these devices.
Detecting gamma rays with "non-imaging" detectors
Is there some way to create a "telescope" which could observe the entire sky for gamma rays, all at once? The answer is "yes", but the systems which astronomers have devised don't look much like any traditional telescopes.
Back in the 1990s and 2000s, the Milagro gamma-ray observatory gathered observations. It was basically a very large swimming pool, covered with a tarp:

Image courtesy of
the University of Maryland Milagro group
Inside the pool were TWO arrays of PMTs: one floating just below the surface of the water, about 1.5 meters deep, and the other sitting on the bottom of the pool, 6 meters below the surface. The two arrays allow one to distinguish between air showers caused by (original) gamma-rays and (original) protons striking the atmosphere.

Image courtesy of
the University of Maryland Milagro group
The idea here adds one extra step of indirection between the original gamma-ray photon and the eventual detection on the ground. In this method,
The direction from which the original gamma ray came can be reconstructed if one has very precise arrival times for the light from each PMT. (Click image below to start animation)

Movie courtesy of
Miguel F. Morales
The Milagro detector was shut down some years ago, in order to build a bigger, better gamma-ray telescope: the High Altitude Water Cerenkov (HAWC) Gamma Ray Observatory . This is a large collaboration of universities in the USA and Mexico. The instrument itself is located on a mountain near Puebla, Mexico, at an altitude of 4100 meters.
HAWC consists of 300 tanks of water, each about 7 meters in diameter and 4 meters high.

Image courtesy of
the HAWC collaboration
Within each tank are three small PMTs and one larger PMT in the middle.
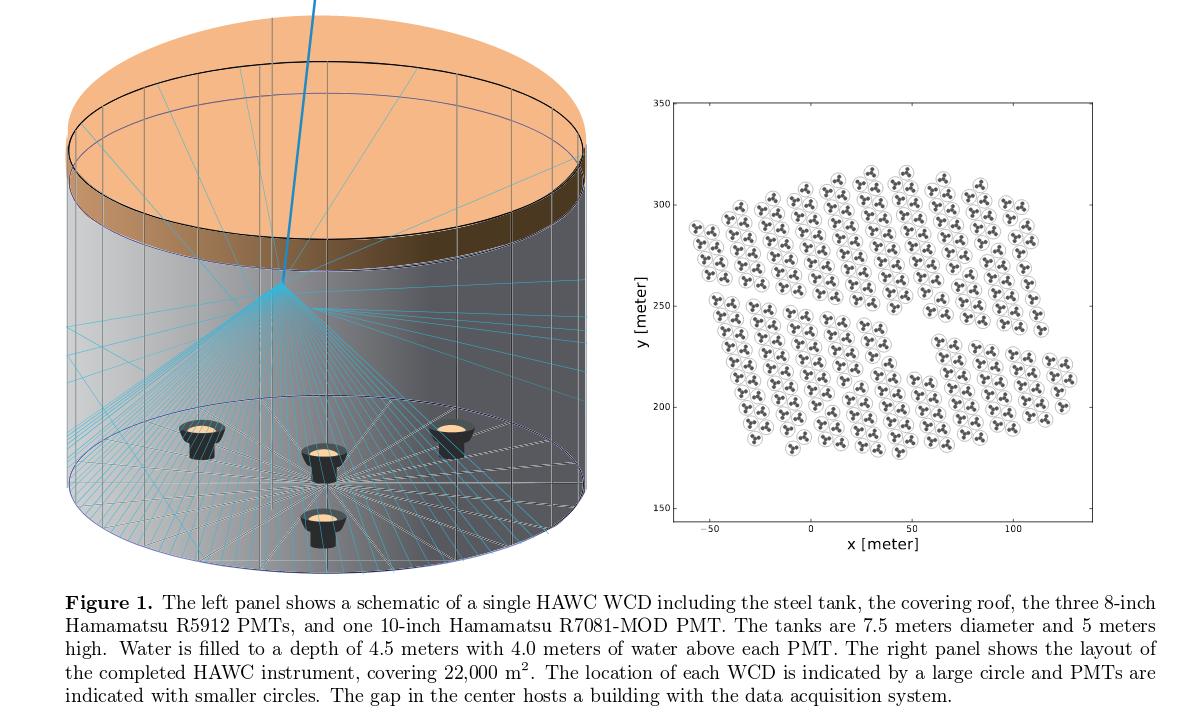
Figure 1 taken from
Abeysekara et al., ApJ, 843, 39 (2017)
HAWC records a "hit" when at least 28 different tanks register photons within a space of 150 nanoseconds. The times recorded by different tanks allow the direction of the original photon to be derived with a precision of roughly one degree, or somewhat better for the highest-energy events.
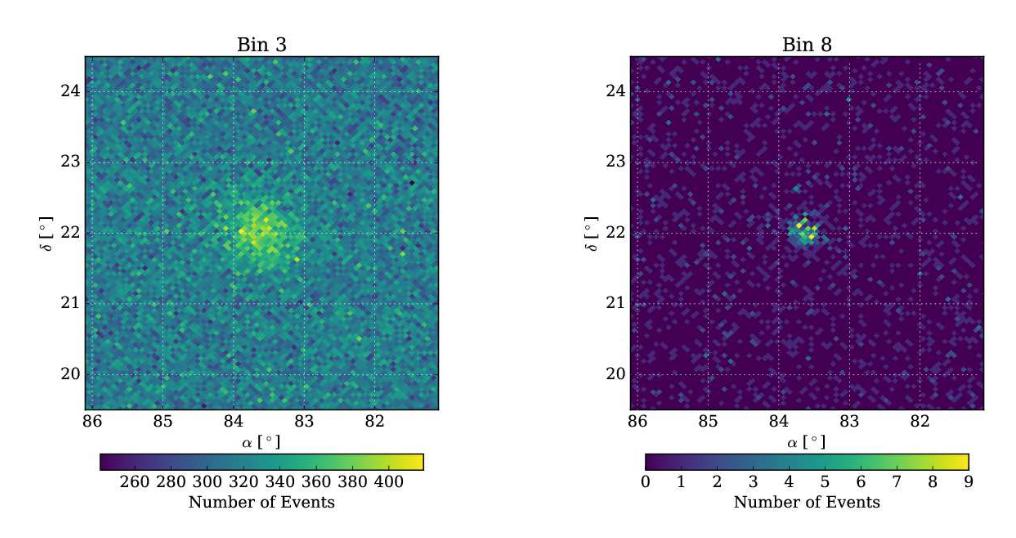
Portions of Figure 8 taken from
Abeysekara et al., ApJ, 843, 39 (2017)
The distribution of hits recorded across the array of tanks can give clues to the origin of the air shower. The larger the fraction of PMTs triggered by a shower, the better the team can distinguish between a photonic (gamma ray) or hadronic (proton) origin.
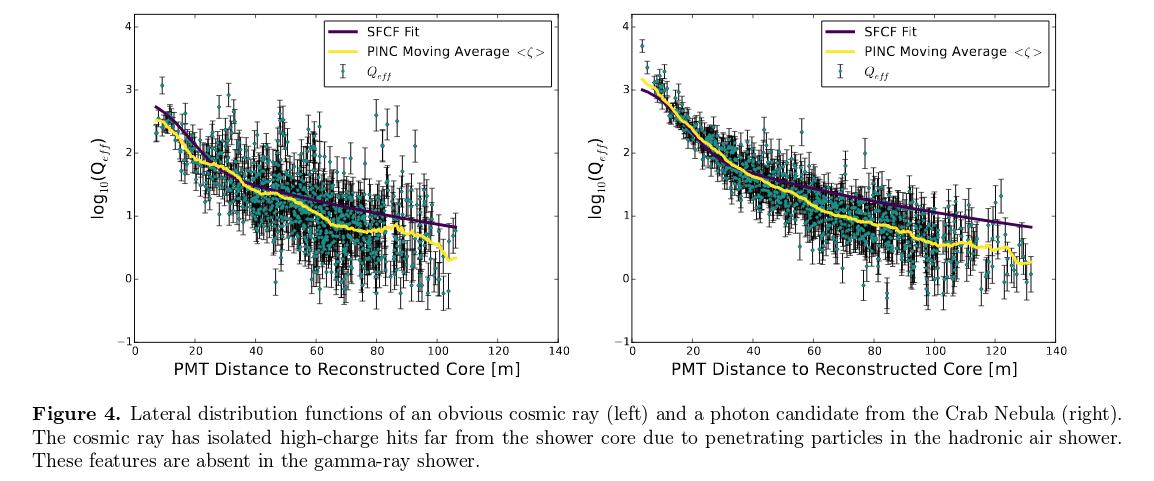
Figure 4 taken from
Abeysekara et al., ApJ, 843, 39 (2017)
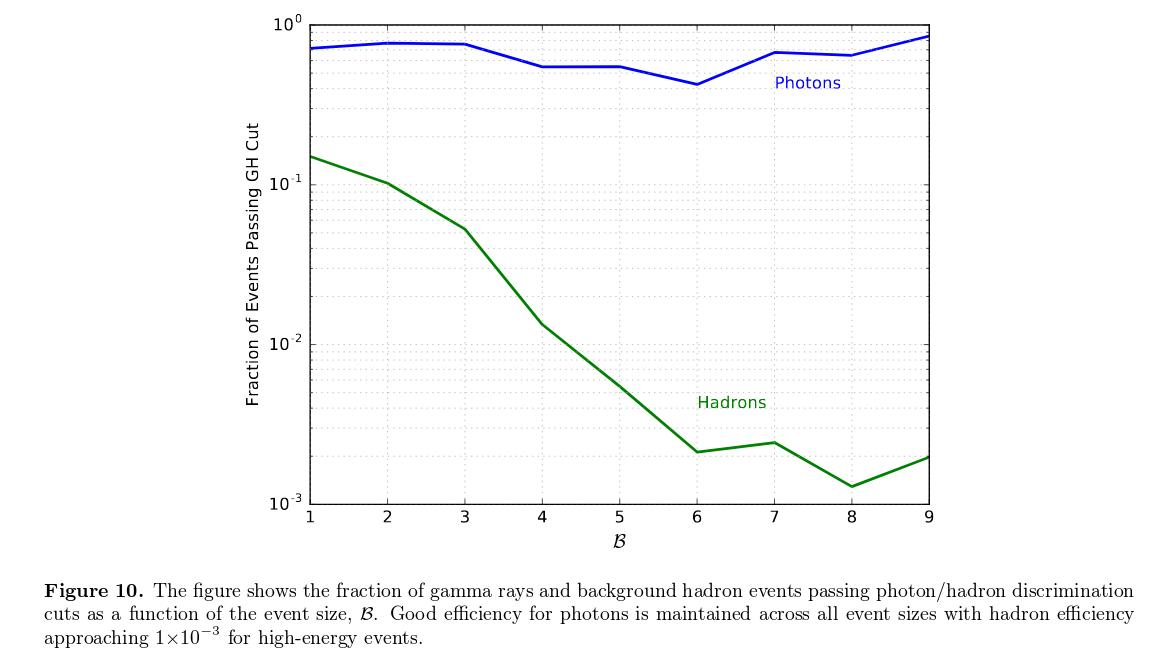
Figure 10 taken from
Abeysekara et al., ApJ, 843, 39 (2017)
Like the "imaging" Cerenkov detectors, HAWC is more efficient at recording gamma-ray photons with very high energies:
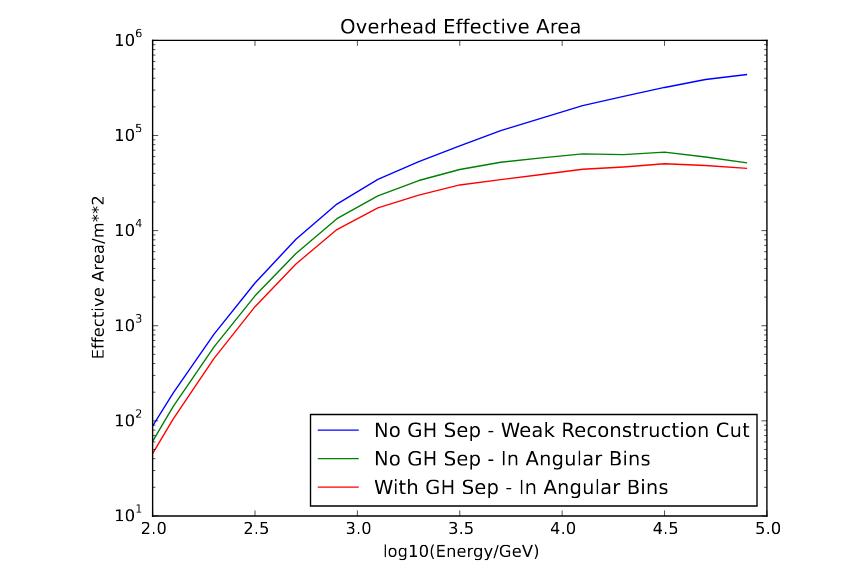
Figure 14 taken from
Abeysekara et al., ApJ, 843, 39 (2017)
Since HAWC can detect air-shower particles from any direction (though it has trouble analyzing showers which are low in the sky), it can monitor very large regions of the sky. At a recent meeting, the team unveiled a gamma-ray map of the sky at TeV energies:

Figure courtesy of
HAWC collaboration.
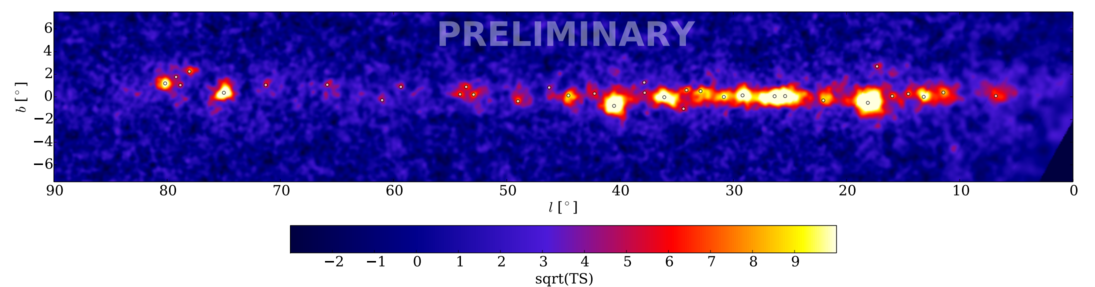
Figure courtesy of
HAWC collaboration.
Q: Can you make a map of this same region of the
galactic plane at other wavelengths, using Aladin,
and identify any of these gamma-ray sources?
I used Aladin to create some maps covering similar regions of the sky:
A more recent version of HAWC's map of the galactic plan shows a few more sources (up to 20!), and good agreement with maps made by the HESS Observatory .
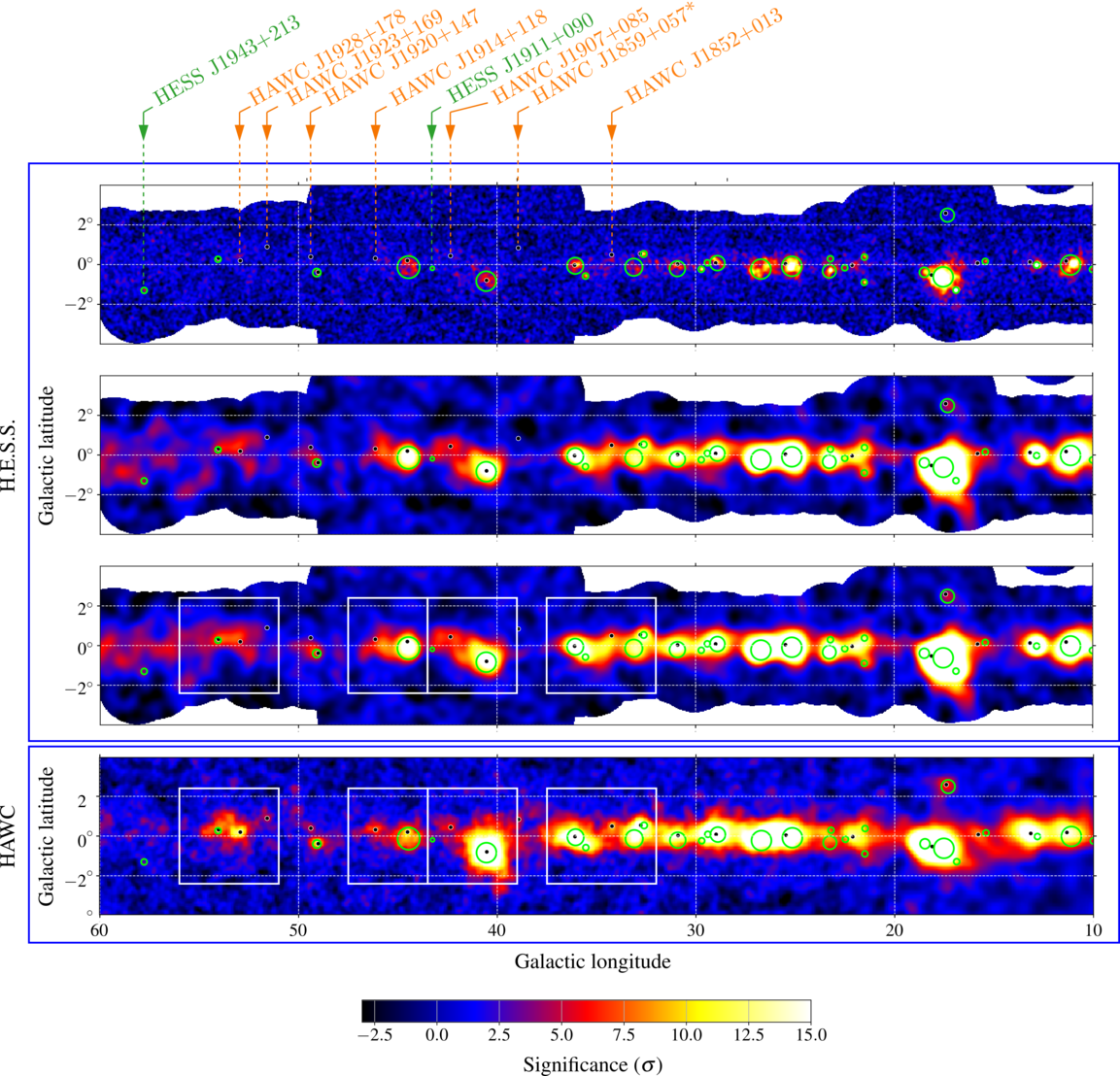
Image courtesy of
H.E.S.S. and HAWC Collaborations
What are the sources of very-high-energy gamma rays?
Now that we know a bit about the manner in which gamma rays of TeV energy are detected, we can ask some questions about their origin. A good place to start is with the map of the TeV sources detected by HAWC:

Figure courtesy of
HAWC collaboration.
Q: What types of object are the 4 named sources in the HAWC map?
The answer is
Q: Why aren't there any (ordinary, main sequence) stars?
The simple answer is that thermal sources just aren't hot enough to produce TeV gamma rays.
Q: You may recall the relationship between the temperature
of an object and the peak of its blackbody radiation:
3 x 10-3 m*K
λpeak = -----------------------
T (K)
What temperature would be required to create a blackbody
spectrum with a peak wavelength corresponding to 1 TeV?
These ultra-ultra-high-energy gamma rays must be produced by some non-thermal processes. There are a number of possibilities.
One is inverse Compton scattering, in which a relativistic electron smashes into an ordinary photon and turns it into a super-high-energy gamma ray. You can read more about this process elsewhere
but the important point, for present purposes, is that there is a pretty simple relationship between the original wavelength of a photon, the speed of the electron which smashes into it, and the final wavelength of the photon:
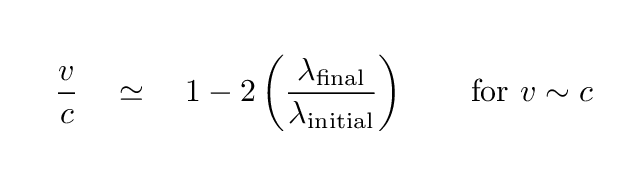
Let's see just how close to the speed of light an electron must be in order to turn an "ordinary" photon into one of the TeV gamma rays seen by HAWC and other ground-based detectors.
Consider an ordinary photon, produced by thermal processes
in a very hot gas, in which T = 10 million Kelvin.
a) what is a typical wavelength for this photon?
b) what is the wavelength of a 1 TeV gamma ray?
c) using the equation above, estimate the speed v
of the electron which is required to convert
the ordinary photon into the gamma ray
d) what is the "gamma factor" or "Lorentz factor" for this electron?
That seems ... pretty fast. Are there really astrophysical sources of such hyper-relativistic particles? It's possible that the jets produced by AGN can create a few particles with such high gamma factors, but it's not easy.
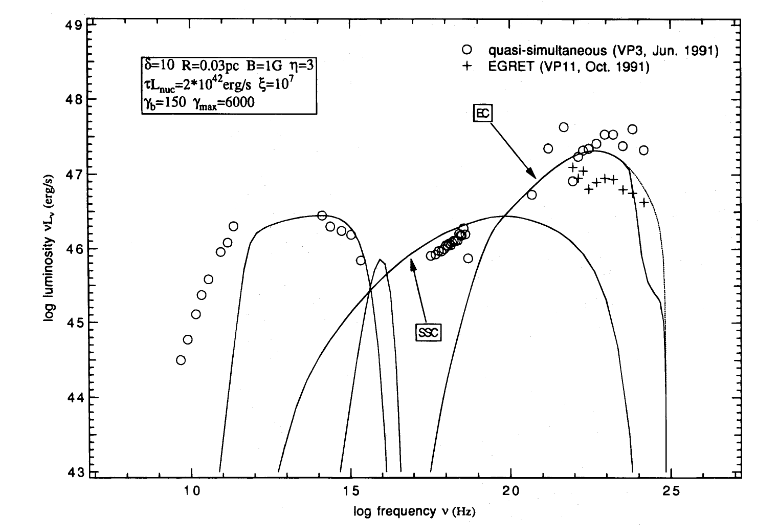
Figure 1 from
Inoue and Takahara, ApJ 463, 555 (1996)
Another possibility for accelerating particles to such high speeds involves shocks and magnetic fields. This is a topic I don't understand, but a good phrase to use while searching for answers is "Fermi acceleration".
 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.