Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
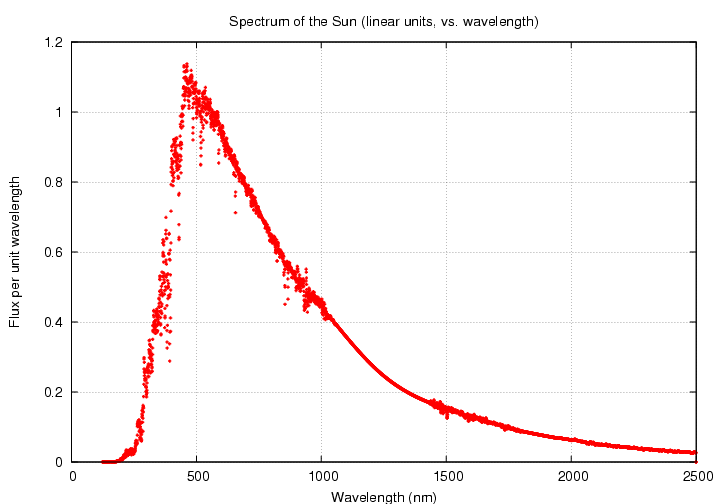
The Sun is a pretty simple object, in some ways. For example, if you look at its spectrum across a wide range of wavelengths, it is not too far from that of a blackbody. You can see the characteristic sharp drop at short wavelengths and gradual decrease at longer wavelengths.
Q: What is the peak wavelength of the solar spectrum? Q: What is the effective temperature of the Sun?
The spectrum's shape will look different if we plot it in logarithmic units ...
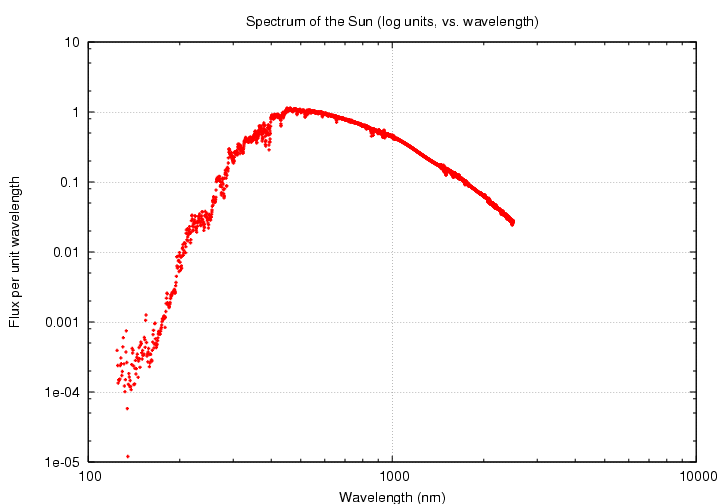
... and even more different if we switch the horizontal axis to frequency instead of wavelength ...
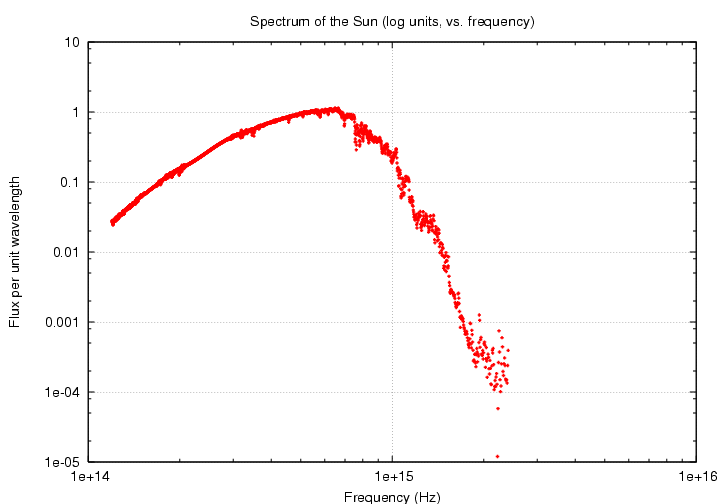
... but one can still recognize the basic form of a blackbody curve.
Galaxies are, in large part, collections of stars. So we might expect the spectrum of an ordinary galaxy to resemble that of a star, or a blackbody. And for some galaxies, that's true. Here are a set of spectra from some ordinary spiral galaxies, taken from The Spectral Energy Distribution of Normal, Starburst, and Active Galaxies. by Schmitt et al., Astronomical Journal, 114, 592 (1997).
On the other hand, there are some objects which have very different spectra. Consider, for example, the galaxy called "Markarian 521." Through an optical telescope, it looks like a little fuzzy patch of light:
However, if one observes this particular galaxy with instruments which cover a very wide range of wavelengths, one measures a spectrum which looks, well, sort of double. Although the points are a bit scattered, it looks as if there are TWO blackbody spectra here. We could call them
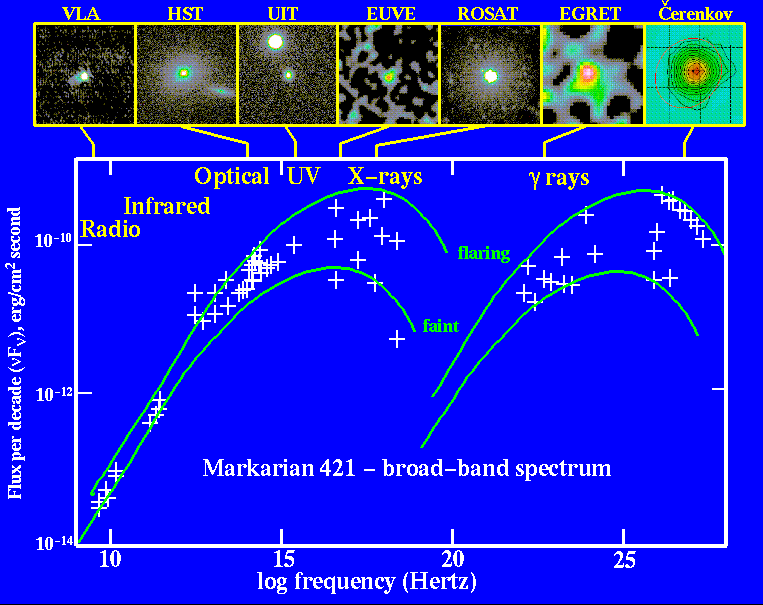
Thanks to Bill Keel's collection of AGN data
Q: What is the peak frequency of each half of this spectrum?
Q: What is the peak wavelength of each half of this spectrum?
Q: If each half were produced by a blackbody,
what temperature would it have?
The "soft" portion of the spectrum could be produced by material at realistic temperatures: millions of degrees. At those temperatures, molecules break into atoms, and atoms are stripped of most or all of their electrons. We call matter in that state a plasma. There are several situations in the universe which can raise matter to millions of degrees. In Markarian 521, as matter circles around a supermassive black hole at the center of the galaxy, collions between orbiting atoms heat the inner portions of the accretion disk.
Image taken from the Chandra Observatory's guide to supermassive black holes
However, the "hard" portion of the spectrum is just too energetic to be created by any ordinary blackbody. Atoms and some subatomic particles would break down at the temperatures indicated by the naive calculation, and so the processes which generate the blackbody spectrum would not occur.
So, what creates the super-energetic radiation emitted by this object? One clue is that the "hard" portion looks very much like the "soft" portion, just shifted to higher energies and higher frequencies.
The ordinary Compton Effect describes what happens when a photon runs into a stationary electron.
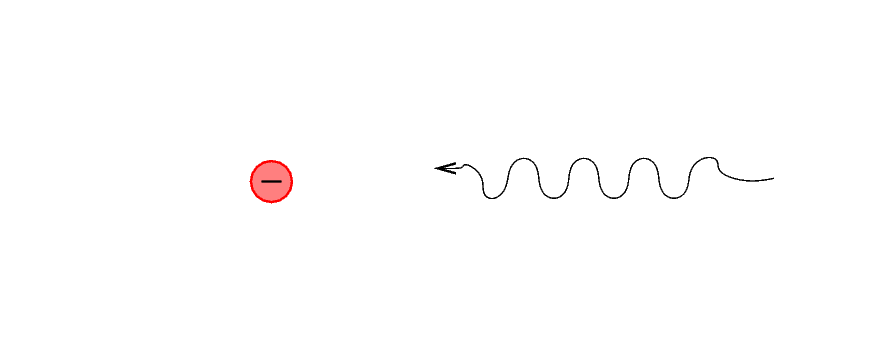
You should already know how to figure out the final wavelength or frequency or energy of the photon in this case.
But ... what if the electron is moving? That is, what if the photon is minding its own business, and a speeding electron slams into it?
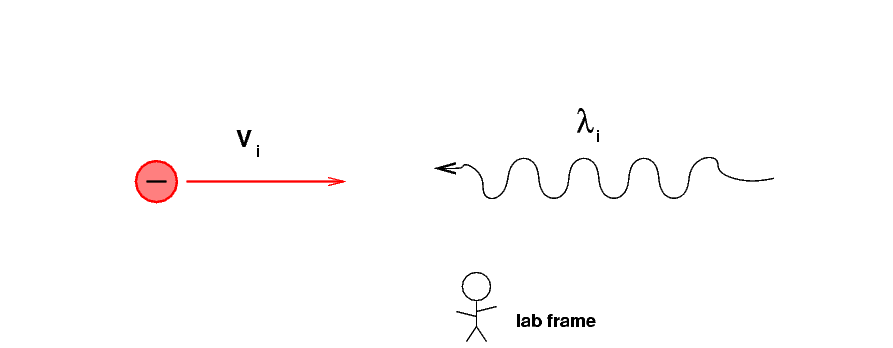
We can solve this problem using ideas you've seen already in this class. To do so, we break it into 3 steps.
Before the electron and photon meet, we put ourselves into a reference frame which is moving with the electron. This means that everything else -- people standing in the lab, trees, cars -- are now moving towards the left at the speed Vi.
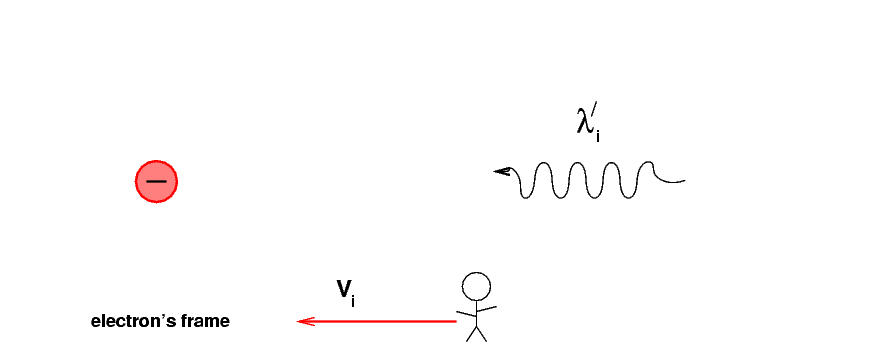
In the lab frame, a student would measure the photon's initial wavelength to be λi. But now, from the electron's point of view, what is the new wavelength of the photon? Call it λ´i (that's supposed to be "lambda-prime sub i"). We'll use primes to indicate quantities measured in the electron's frame.
Q: What is the general formula for the new wavelength λ´i?
Q: Suppose the original photon was optical light
with wavelength 500 nm, and the speed of the
electron is v = 0.99 c .
What is the new wavelength?
In this new reference frame, the electron is at rest. We can use the conservation of energy and momentum to figure out the wavelength of the photon after it has collided with the stationary electron. Suppose that it bounces straight back along its original path.
Q: What is the general formula for the scattered wavelength λ´f?
Q: Suppose the original photon was optical light
with wavelength 500 nm, and the speed of the
electron is v = 0.99 c . Suppose that
the photon is scattered straight back in the
direction of motion. What is the scattered wavelength?
Now we go back to the original, "lab frame", in which students, trees and tables are all at rest.
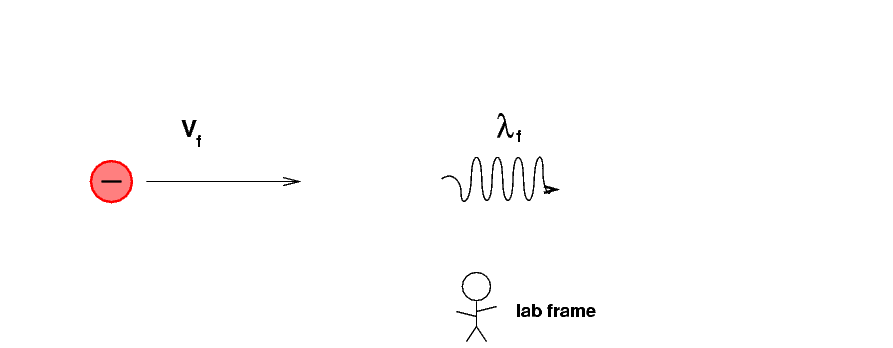
We need to convert the photon's final wavelength in the electron's frame to its value in the lab frame. Look very carefully at the picture ...
Q: What is the general formula for the final wavelength λf?
Q: What is the final wavelength for our example of original
wavelength 500 nm, v = 0.99 c, and perfect
backscattering?
The net result of this process is that very energetic electrons transfer some of their energy to photons by smashing into them. We call this inverse Compton scattering. In regular Compton scattering, it is the photon which gives energy to a stationary electron; in the inverse process, the photon gains energy.
Okay, we now know that if a photon of original wavelength λi is struck by an electron moving at speed v, so that the photon is perfectly backscattered, the final wavelength of the photon will be
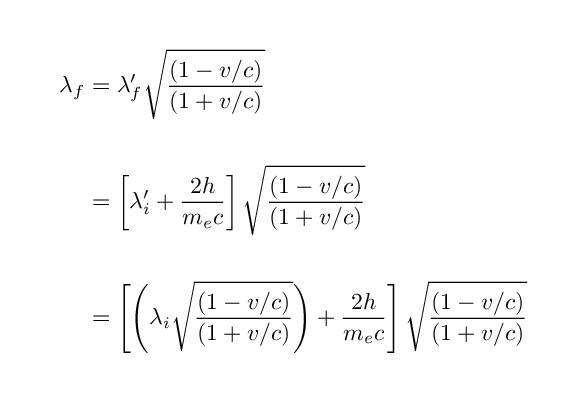
Hmmmm. This is a messy expression. Can we simplify it?
Well, maybe. Look at the term involving Planck's constant and the mass of the electron.
2 h
Q: What is the wavelength corresponding to ------ ??
me c
If the original wavelength, as seen in the electron's frame of reference, λ´i, is much larger than this factor, then the shift due to Compton scattering will be small; small enough, perhaps, that we can ignore it. Let us assume that
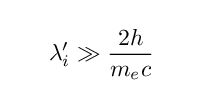
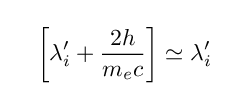
so that we can approximate
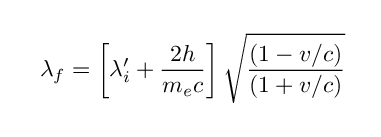
by the simpler formula
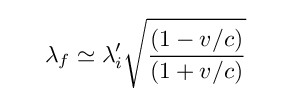
In this regime, the final wavelength of the scattered photon can be written as
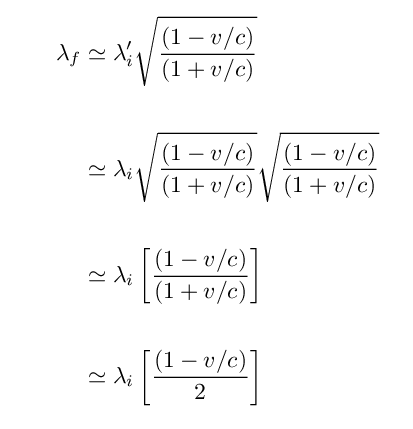
In the last step, I've assumed that the electron's speed is very close to the speed of light.
That means that if we know the original and final wavelengths, we can estimate the speed of the electron:
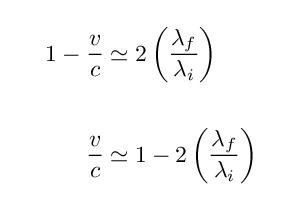
Suppose that the "hard" portion of this spectrum is really just a set of photons from the "soft" spectrum which have been boosted in energy and frequency by collisions with a beam of energetic electrons. In other words, what if a photon originally near the peak of the "soft" spectrum collided with an electron so that it become a photon near the peak of the "hard" spectrum?
Q: What is the ratio of final to initial frequency? Q: What is the ratio of final to initial wavelength? Q: What speed must the electrons have to cause this shift?
Those are some fast electrons! We do see other evidence for such jets of ultra-relativistic material near the center of active galaxies. We think that somehow (and we're not sure), a small fraction of the material spiralling into a black hole is shot outwards perpendicular to the accretion disk at very high speeds. The material in this jet may collide with an "ordinary" photon emitted by the hot material in the disk, creating a shifted version of the photon.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.