Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
In the early 1920s, physicists were divided on the fundamental nature of light. Was it a wave, or was it a particle (the photon)? Most experiments indicated that it behaved like a wave, but there was some evidence that it might have particle-like properties, too. Arthur Holly Compton performed the definitive experiments in the early 1920s which convinced just about the entire physics community that light COULD, at times, act very much like a particle.
In his honor, we call one particular sort of interaction between light and material particles Compton scattering.
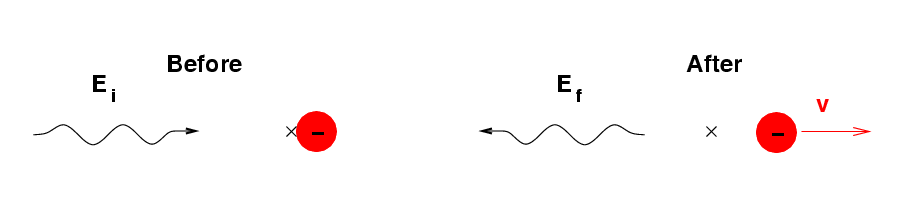
Let's begin with a very simple case: a photon runs into a stationary electron, bounces off it, and flies back exactly whence it came.
The total energy of the two particles must be the same before and after the collision.
Q: What is the total energy before
the collision?
What is the total energy after
the collision?
Q: How does the "final" photon
compare to the "initial" photon?
more energetic
the same energy
less energetic
The total momentum of the particles must be the same before and after the collision, too.
Q: What is the total momentum before
the collision?
What is the total momentum after
the collision?
You should end up with two equations connecting two unknown quantities.
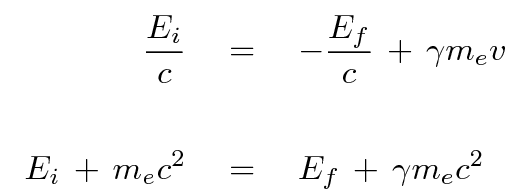
It is possible to solve for the final energy of the photon, and for the speed of the electron, after a lot of work. The result is
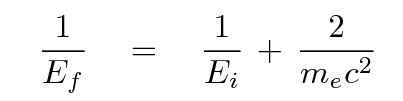
Let's check and make sure that this works. Suppose we start with a photon in the middle of the X-ray range, with an energy of E = 10 keV = 1.6 x 10^(-15) Joules.
Q: What is the initial total energy?
What is the final total energy?
Q: What is the final speed of the electron?
Express as m/s and as a fraction of c.
What is the gamma factor of the electron?
Q: What is the initial momentum?
What is the final momentum?
Okay, that seems to work. Hmmm. The energy of the "final" photon was pretty close to the energy the "initial" photon, wasn't it? The final speed of the electron was pretty small compared to c, too. That doesn't seem very interesting.
Let's look at the results if we start with a more energetic photon.
initial final final final
photon energy photon energy electron speed electron gamma
-------------------------------------------------------------------------
10 keV
1.6 x 10^(-15) J
100 keV
1.6 x 10^(-14) J
1000 keV
1.6 x 10^(-13) J
10 MeV
1.6 x 10^(-12) J
1 GeV
1.6 x 10^(-10) J
-------------------------------------------------------------------------
You may notice several things from this exercise.
Suppose that we sent a photon with a (nearly) infinite initial energy into the collision. What would the final energy of the resulting photon be?
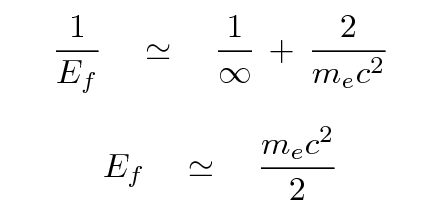
Why can't the photon carry away any more energy from the collision? Well, one way to answer the question is to say, Solve the equations of conservation of energy and momentum, and whatever comes out, comes out. Sometimes it helps if there is a little idea attached to the math, just to jog one's memory. If the photon carried away lots of energy above the rest energy of the electron, it might not BE a photon; instead, it might create an electron/positron pair of particles, so that the interaction would look like this:
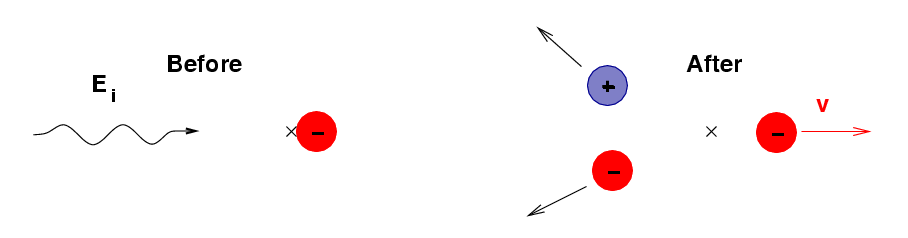
Now, the only situation we have considered is a collision in which the photon bounces straight back in the direction from which it came. It is also possible (and much more likely) for the outgoing photon to fly off at some other angle:
The results are a bit more complicated in this case, since one must now consider the conservation of momentum in two directions. However, the relationship between the initial and final energies of the photon looks similar to the simple equation shown above.
If you want to see the solution for this more general case, go look at my notes on the Compton effect from my Modern Physics course.
If you: start with X-rays or gamma-rays and shine them on a block of matter you get: high-energy electrons (and lower-energy photons)
But the process can also work in reverse:
If you: start with relativistic electrons and fire them into a bunch of low-energy photons you get: high-energy photons (and lower-energy electrons)
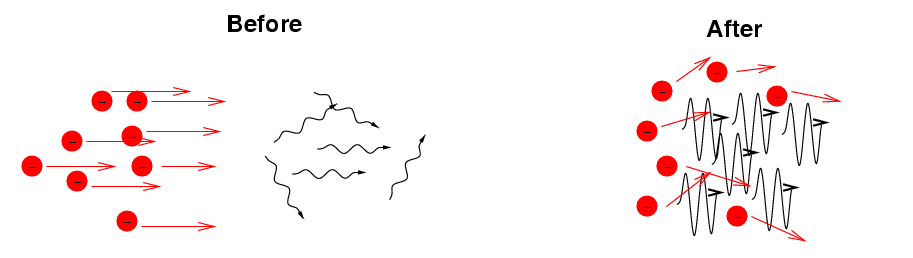
Now, here on Earth, relativistic particles aren't very common. But there are places in the universe which do create highly relativistic electrons in great numbers; for example, jets emitted from accretion disks around supermassive black holes.
If the jet happens to be pointing towards the Earth, then its electrons will collide with low-energy photons coming from the accretion disk (or from stars in the galaxy), boosting those photons to much higher energies.
For example, the galaxy called "Markarian 521" doesn't look very unusual in pictures taken by optical telescopes: it's just a small spiral galaxy.
However, if one takes a spectrum of this galaxy with a very wide range of instruments, one sees a strange sort of "double spectrum":
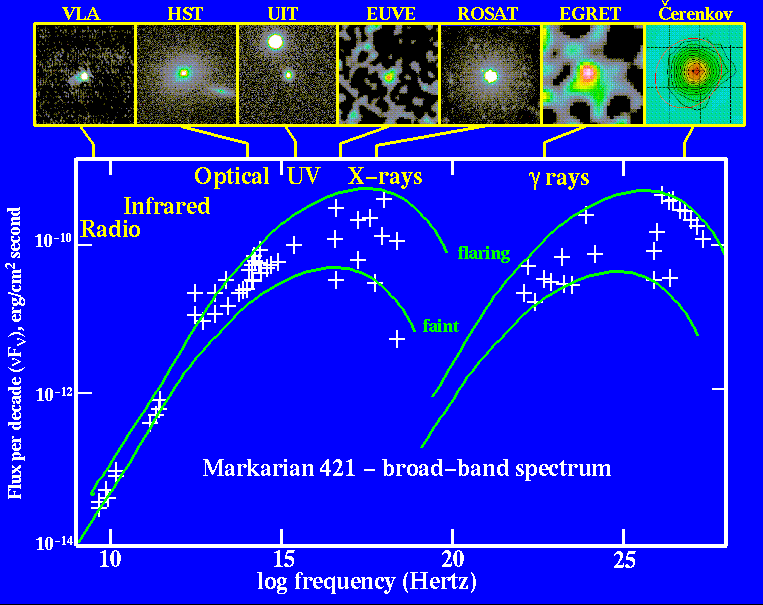
On the left-hand side of this graph, you can see what looks like the spectrum of a galaxy with a big accretion disk at its center: most of the energy is emitted in the ultraviolet and soft X-ray region. The right-hand side of the graph shows a very unusual amount of ultra-high-energy gamma-ray emission. We think that what's happening is that the "ordinary" photons are being boosted in energy by a factor of roughly 10,000,000 due to collisions with extremely energetic electrons in a jet which is coming nearly straight towards us.
In a more detailed description of the inverse Compton effect, you can find a formula which yields an approximate relationship between the original and final energies of a photon, and the speed of the electron which collides with it:
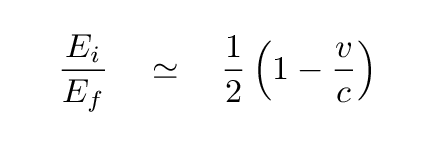
Q: How fast must the electrons in the jet
of Markarian 421 be moving?
What is their gamma factor?
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.