Calculations of overall system throughput

Michael Richmond
Jan 2, 2017

What fraction of the light entering the WIYN 0.9-m Telescope is captured and measured by HDI? The answer to this question can be very important for observers who are planning an observing run and trying to estimate the exposure time required to achieve some particular signal-to-noise ratio on a certain target.

In order to answer this question, I made use of images collected by Allyn Smith and Spencer Buckner of Austin Peay State University on two nights; comments from night logs are shown below.

• May 10, 2016: "Weather: clear", "excellent night"
• Dec 18, 2016: "Weather: clear to partly cloudy with occasional mostly cloudy", "Skies were mostly clear for most of the night, but clouds rolled in around 2am"

The images I'll use from Dec 18 were taken before midnight, so I believe the sky should have been clear at that time.

The stars used for these calculations are a pair of hot subdwarfs, commonly used for spectrophotometric calibrations:

• BD +17 4708
• BD +26 2606

The observations used for calibration were acquired through the SDSS ugriz filter set, rather than the Johnson-Cousins UBVRI filter set. I'd like to do a set of calculations in the future using the UBVRI set; if any reader happens to have an existing dataset which could be used for this purpose, please let me know.

Starting assumptions

I made the following assumptions for some of the parameters in the calculations:

telescope size

Primary mirror diameter = 36 inches, and second mirror diameter = 17 inches. The former seems pretty obvious from the original name of the telescope, and the latter is shown in the detailed drawings listed on the WIYN 0.9-m Observatory "Technical Information" page.

mirror reflectivity

Direct measurements of the reflectivity from the freshly-cleaned aluminum surfaces of the actual WIYN 0.9-m mirrors can be found at the WIYN 0.9-m "Technical" webpage. I read values for the 'g' and 'r' passbands from the graph showing 2012 measurements.

However, these measurements only cover the range 400 - 700 nm, which does not include much of the 'u', 'i', and 'z' passbands. Therefore, I looked for reflectivity measurements covering a wide range in other sources. I settled on measurements of an aluminum coating for the Gemini South mirrors which is described in Gemini South's Secondary Mirror Sports Shiny Silver Coat.

The values I adopted for a single reflection are

                     u           g         r          i           z
    --------------------------------------------------------------------
     one bounce    0.910       0.912     0.895      0.875       0.890
    --------------------------------------------------------------------
       

Of course, I accounted for two reflections in the calculations.

atmospheric extinction

I didn't have enough data to derive extinction coefficients from 0.9-m observations themselves, and I couldn't find any values listed in the literature. The best I could do was a set of measurements made at CTIO by Douglas Tucker in Nov, 2012. The values taken from this reference are magnitudes per airmass.

                     u           g         r          i           z
    --------------------------------------------------------------------
         k          0.44        0.20      0.10       0.06        0.07
    --------------------------------------------------------------------
       

filter passbands

One of the steps in the calculations involves computing the number of photons received from the star Vega. I used the following versions of the SDSS passbands for that purpose. Note that each dataset has a peak transmission value of 1.00, or 100 percent. In real life, any filters (including those at Kitt Peak) will have lower peak transmissions. That means that my "expected" number of photons will be over-estimates, and thus the derived values for throughput will be under-estimates.

This error is likely to be largest in the u-band.

filter	passband data
u	sdss_u.pass
g	sdss_g.pass
r	sdss_r.pass
i	sdss_i.pass
z	sdss_z.pass

spectrum of Vega

One of the steps in the calculations involves computing the number of photons received from the star Vega. I used the following spectrophotometric data for those calculations, based on values provided by Ralph Bohlin at some point prior to 2006.

vega_spectrum.dat

standard-star magnitudes

I convolved the SDSS passbands with the spectrum of Vega in order to compute the number of exo-atmospheric photons which ought to be received from that star, per second, per square centimeter of collecting area. In order to calculate the number of photons received from the observed stars (which are much fainter than Vega), I simply scaled this number of photons by a factor based on the magnitude difference between Vega and the fainter star:

                              -0.4*( star_mag - Vega_mag)
                factor  =   10
 
      

What are the appropriate magnitudes for Vega and the standard stars in the SDSS system? For Vega, I adopted those listed by UBVRI-ZY and ugriz zeropoints from 20 calspec standards, (Pickles, 2010 HST calibration workshop). For BD+174708 and BD+262606, I took values from Smith et al., AJ 123, 2121 (2002).

star	u	g	r	i	z
Vega	0.974	-0.093	0.148	0.372	0.513
BD+17 4708	10.56	9.64	9.35	9.25	9.23
BD+26 2606	10.761	9.891	9.604	9.503	9.486

instrumental magnitudes

The reductions of the images of the standard stars was pretty basic.

• subtract bias using overscan region
• create median flatfields for each night in each filter
• divide target frames by flatfields
• measure aperture photometry of target star in circular aperture of radius 10 arcseconds, with background estimated using an annulus of radii 12.9 to 17.2 arcseconds

I used the XVista image analysis package to carry out these tasks.

counting electrons

I converted the number of counts-above-sky within the aperture into electrons by using a gain value of

            gain  =   1.3 electrons per count 
      

as derived in, for example, Technical Note 8.

One minor note: since the first step in dealing with the raw images was to divide all pixel values by 2 (to keep all data values within the range of 0 - 32767), I actually multiplied the number of counts within the aperture by 2*1.3 = 2.6.

Results

There are several ways to express the "throughput" of a telescope and its detector. I'll choose two particular definitions:

electrons counted / photons into telescope aperture

This is probably the most widely used choice, corresponding to a "total system throughput". Compute the number of photons entering the front aperture of the telescope during an exposure, and compare to the number of electrons counted by the CCD.

The results for "overall system throughput" are shown below.



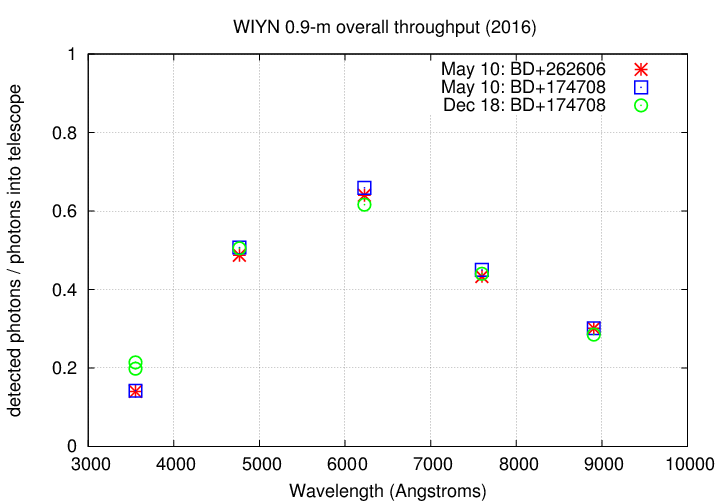
Estimates from two different stars, and from two different nights, agree at the level of a few percent. The system is most efficient, just above 60 percent, in the SDSS 'r' band, around 6000 Angstroms. At a guess, the Johnson-Cousins V and R filters are probably about equally good.

electrons counted / photons reaching filter

For this version, we try to remove the light lost due to the two reflections, from the primary and secondary mirrors. What remains should be the throughput of

               filter(s) + dewar window + CCD

        

The results for "throughput after reflections" are shown below, in bold black symbols; the previous, overall-system, values are shown in lighter, colored symbols.



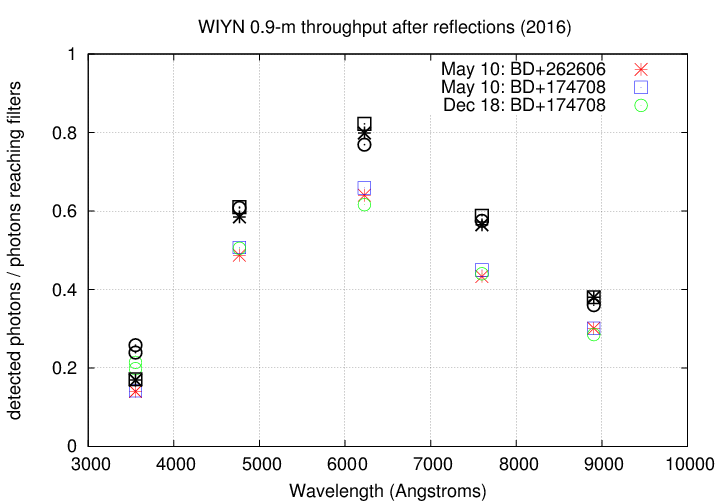
Since the reflectivity of aluminum decreases toward the red side of the optical spectrum, we see the greatest change in the i and z passbands.

The shape of this response is -- not surprisingly -- rather similar to the spectral response of the e2V 231-84 CCD chip.