Errors incurred in transferring calibration from bright stars to faint

Michael Richmond
Oct 29, 2008
Oct 30, 2008

This document makes a first attempt to quantify the errors which occur when one transfers calibration from a bright star to a faint one. This document DOES address the following facets of the issue:

• observations of bright and faint stars in the same field
• choice of step size between bright and faint stars
• noise from the sky background
• readout noise in the detector

This document does NOT address the following facets:

• mismatch between actual and expected spectral type of stars (though this can easily be done in an extended version of my code)
• errors in the transmission function of the overall instrument passband (though this can be easily be done in an extended version of my code)
• dark current (though this can be easily be done in an extended version of my code)
• gradients in illumination across the focal plane due to shutter motion

The method: simulating a series of images

The basic idea is simple: start with a bright star of magnitude M = 11 which is presumably calibrated, to some degree, in absolute flux. Observe this star with an exposure time which will yield a high signal-to-noise ratio (without saturating the detector). In the same exposure, measure the light of a star which is fainter by delta magnitudes. We can use this observation to calculate

       faint star mag  =  bright star mag  + delta

That will move us one step from the bright star to the goal of a very faint star of magnitude m = 25.

If the process of taking the image, or measuring its properties, involves any error, then our "measured magnitude" for the faint star will differ slightly from the "true magnitude", which is simply M + delta.

We then increase the exposure time and repeat the process, this time treating the faint star as the "bright" one, and choosing a new "faint" star which is delta magnitudes fainter. Each new field brings us one step closer to the goal. When we reach a star of magnitude m = 25, we stop and see how much the differences between the "true" and "measured" magnitudes have accumulated.

The detailed, step-by-step procedure within each step goes something like this:

1. start with the "bright" star's true magnitude
2. pick spectral types for both "bright" and "faint" stars (in this test, I used Vega in every case)
3. create a scaled value of the spectrum which will have the known "true" magnitude in V-band
4. create a gaussian PSF, based on the diffraction limit of the optics
5. compute a safe exposure time, such that the peak number of counts in the central pixel would be at 80% of the full-well depth of the detector, IF the star were to fall at the center of a pixel
6. calculate the contribution of the sky background for this exposure time
7. generate a synthetic image which includes
   • the bright star
   • the faint star
   • sky background
8. find stars in the image
9. measure the aperture magnitude of each star
10. compute the observed different delta' between "bright" and "faint" star
11. compute the magnitude of the "faint" star in the calibrated system
12. go on to the next step, making the "faint" star into the "bright" star; return to step 1

In practice, I repeated steps 7-11 some number of times, in order to reduce the statistical errors. This is equivalent to taking N images of each bright/star pair.

A noiseless test

In order to verify that the simulation did not have mistakes of some sort, I ran the test with no noise; in other words, when I generated images using no photon noise in the signal from the bright star, or the faint star, or the background sky. In this special case, we expect that, in each step from M = 11 to m = 25, the "observed" magnitude difference delta' should be exactly equal to the "true" magnitude difference delta.

For the test, I used steps of size delta = 4 mag and the SNAP 8B1 overall passband; see an earlier report for a description of the 8B-series passbands. The 8B1 passband has an effective wavelength of 493 nm. I ran 10 different end-to-end simulations, running from the shortest exposures to the longest.

I The result, after steps involving stars of magnitude V = 11, 15, 19, 23 and 25, was a magnitude of

      true mag=25      observed mag = 25.00229 +/- 0.00054

My simulation code creates images which pixel values which are 16-bit integers, so there is some amount of roundoff in the creation of each star. The accumulated error after 4 images is very small, just about 0.002 mag. As you will see from the tests below, this "simulation error" is small compared to the errors incurred due to real sources of noise.

Simulations with noise

I then ran a series of tests in which I added photon noise to the signals from each star and from the sky background. Let me summarize the results in a table. All tests have

• telescope diameter 1.65 meters
• no secondary obstruction
• focal ratio f/10.5
• pixel size 10.5 microns
• CCD readnoise 5 electrons
• CCD gain 3 electrons per ADU
• CCD full-well depth 100,000 electrons
• exposure time designed to yield 80,000 electrons at peak, for a PSF falling at center of pixel
• random sub-pixel locations for each star
• start mag M = 11
• end mag m = 25
• 10 images of each bright/faint pair
• aperture magnitudes measured with a circular aperture of radius 4 pixels

The minimum exposure time, required for the first step in which the "bright" star is M = 11, is 0.25 seconds for filter 8B1 and 0.65 seconds for filter 8B4.

testname     step-size delta    N(runs)    max exptime    observed faint mag
               (mag)                       (sec)                (mag)
---------------------------------------------------------------------------

              using passband system8B1  (493 nm)

  A              4              10       unlimited     24.98867 +/- 0.00855

  B              6              10       unlimited     24.96804 +/- 0.02934

  C              2              10       unlimited     24.99536 +/- 0.00871


  A2             4              10         1000        25.01703 +/- 0.02445

  A3             4             300         1000        25.00560 +/- 0.02308

  

              using passband system8B4  (850 nm)

  D              4              10         1000        24.99219 +/- 0.03090


---------------------------------------------------------------------------

Note that when there are no limits placed on exposure time, then the time required to build up the desired signal can be very long for the faintest steps. For example, the exposure time required to cause a star of V = 23 nearly to fill the full-well depth is roughly 4.4 hours! That number will shrink in the near-IR because the background sky will contribute much more light.

Below are examples of 1000-second exposures in filter 8B1 (left) and 8B2 (right), showing a "bright" star of magnitude V=23 and a "faint" star of magnitude V=25. In each case, the greyscale runs from white (0 ADU) to black (200 ADU) in a linear fashion.

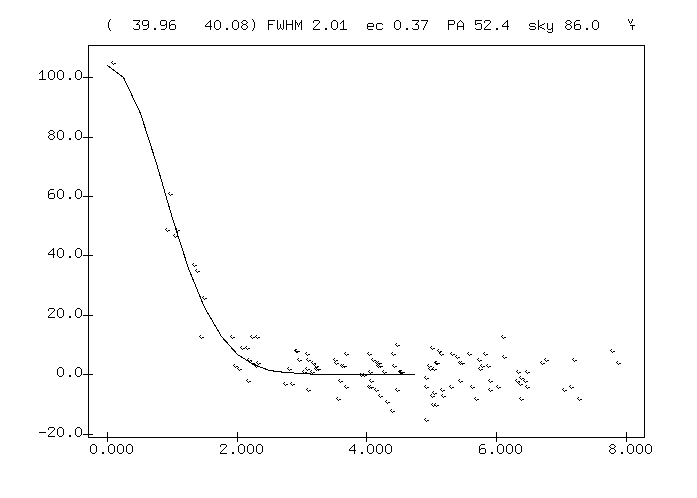
You can get a rough feeling for the signal-to-noise ratio in these images by looking at a radial profile of the "faint" V=25 star. First, for the 8B1 image

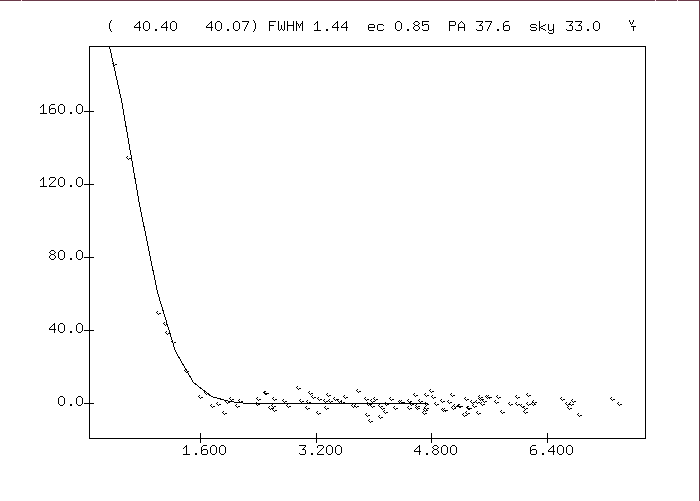
and now the 8B4 image. Note the wider PSF, due to diffraction at this longer wavelength, and the higher sky background.