For some particular satellite mission, how bright a star can we observe without saturating the detectors? In this document, I investigate the question for one particular generic satellite with the following parameters:
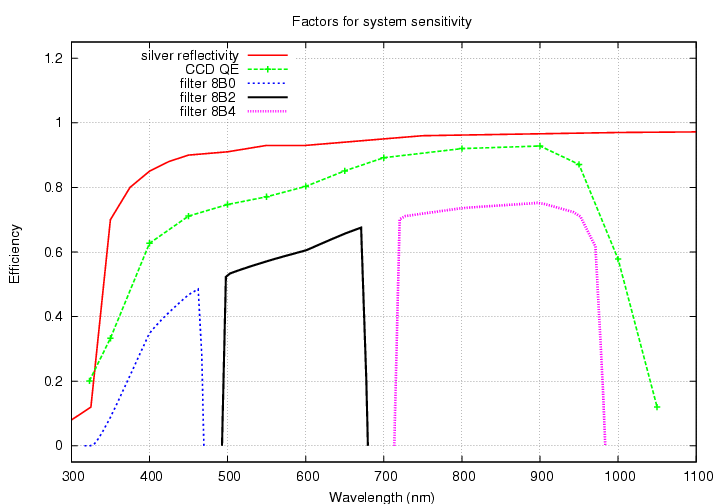
One can compare the importance of these several factors to the overall system throughput:

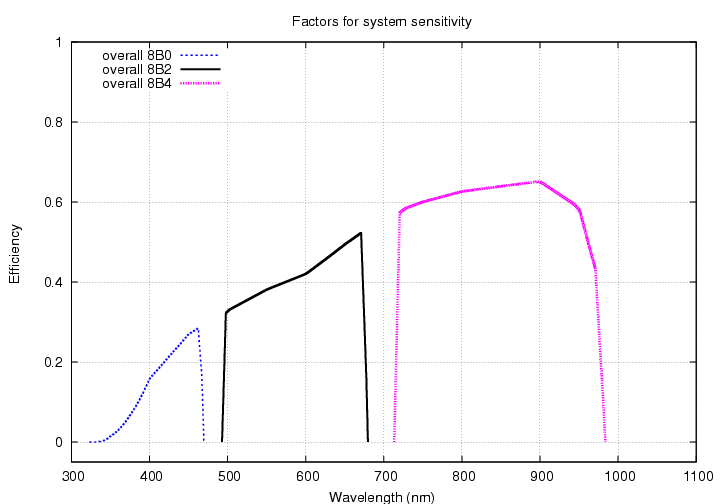
We end up with overall system sensitivity as a function of wavelength within each passband:
I compute stellar fluxes using Vega as a standard source. I'll assume that the magnitude of Vega in any filter is zero; thus, my calculations are on a "Vega-based" system, not an "AB" system. I used a spectrum of Vega supplied by Ralph Bohlin.
I also computed fluxes for two other stars: a G2V star, similar to the Sun, and a K7V star, much cooler than the Sun. These spectra -- not flux calibrated -- were taken from Pickles (1998) . In order to set these stars on the same flux scale as Vega, I did the following:
The result is that the scaled versions of these other stars' spectra will yield the same number of photons as Vega will, when each is observed through a Bessell V-band filter. In other words, I am matching stars of different spectral types only in the V-band; all my scaled spectra will yield magnitudes "V=0".
I then convolved light from these scaled spectra through the overall transmission curves. The result is the number of DETECTED ELECTRONS, per square cm per second, for a star of magnitude V=0. Using the collecting area of the telescope (area = 2.14 sq. meters), I then computed the total number of detected electrons in a single second.
What fraction of these electrons will lie within the central pixel? That depends on the location of the star's center with respect to the pixel grid on the detector. For circular gaussian PSFs on square detectors, we can compute the best case (star falls at corner of four pixels) and worst case (star falls at center of pixel):
![]()
How large will the PSF be? I assumed that the optics were diffraction limited, in which case the size of the PSF depends on the wavelength. Physics states that the half-width of a diffraction-limited spot is roughly, in angular units,
lambda
theta = 1.22 ---------------- radians
diameter
and we can then convert into meters on the focal plane by computing
half_width ~ (theta) * (focal_length) meters
I then made the further assumption that this diffraction pattern was approximately a gaussian, and set the FWHM of the gaussian to (2 * half_width). We end up with
lambda 400 nm 800 nm 1500 nm ------------------------------------------------------------ FWHM 0.98 pix 1.96 pix 2.14 pix
Over this range, the fraction of light falling in the central pixel is approximately linear with FWHM. Using a simple linear approximation, I calculated the fraction of light falling into the central pixel for all passbands.
So, given the total number of detected electrons per second of exposure, and the fraction of those which lie within the central pixel, we can then compute the number of electrons which lie in the central pixel after a 1-second exposure, for a magnitude V=0 star. We can compare that number to the full-well depth of the detector to determine
Below is a table showing the minimum V-band magnitude required not to saturate the detector in a 1-second exposure.
# spectral_type filter lambda min_mag # (nm) vega_spectrum.dat 8B0 426 11.278 vega_spectrum.dat 8B1 495 11.949 vega_spectrum.dat 8B2 593 11.904 vega_spectrum.dat 8B3 712 11.646 vega_spectrum.dat 8B4 845 11.011 ukg2v_mag0.dat 8B0 426 10.574 ukg2v_mag0.dat 8B1 495 11.659 ukg2v_mag0.dat 8B2 593 12.065 ukg2v_mag0.dat 8B3 712 12.191 ukg2v_mag0.dat 8B4 845 11.807 ukk7v_mag0.dat 8B0 426 9.741 ukk7v_mag0.dat 8B1 495 11.323 ukk7v_mag0.dat 8B2 593 12.298 ukk7v_mag0.dat 8B3 712 12.830 ukk7v_mag0.dat 8B4 845 12.721