
 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Table of contents:
On Oct 19, 2005, David Dunham watched the asteroid (166) Rhodope briefly cover the star Regulus. His location for observing this event was near Monesterio in the Badajoz province of Spain. You can see his report at http://iota.jhuapl.edu/mp166.htm.
His equipment included
Each video frame has a time stamped on it. The video file contains frames 720x480 pixels in size, in RGB color, in AVI format. Below is an example, frame number 1 in the sequence.

As far as I can tell, each frame in the movie file contains a combination of two fields of video data. By "field", I mean the light striking the camera during a period of about 1/60 of a second. Since two fields are combined in each frame of the video file, the time stamps show a blur in the least significant digits. In the example above, you can see
After looking at several consecutive frames at the very start and very end of the movie file, I decided that
This yields a frame rate of about 30.03 frames per second.
I processed this movie file in the following manner:
In addition to the first-magnitude Regulus, there are several fainter stars visible in the field

Regulus is labelled "A" in the figure above. I will measure the light from Regulus and the stars marked "B" and "C" in all frames. It will turn out, I think, that the stars are too faint to serve as useful references, but perhaps they may provide information for some purposes.
The 8-bit digitized images had a small dynamic range, from 0 to 255 counts per pixel. Regulus was almost saturated: its peak values were typically between 200 and 250 counts. The sky background near the center of the frame was about 30-40 counts per pixel. The two faint reference stars had peak values only about 10-20 counts above the local background. The FWHM of Regulus was pretty broad, around 6 pixels.
For each of the 142 good frames, I
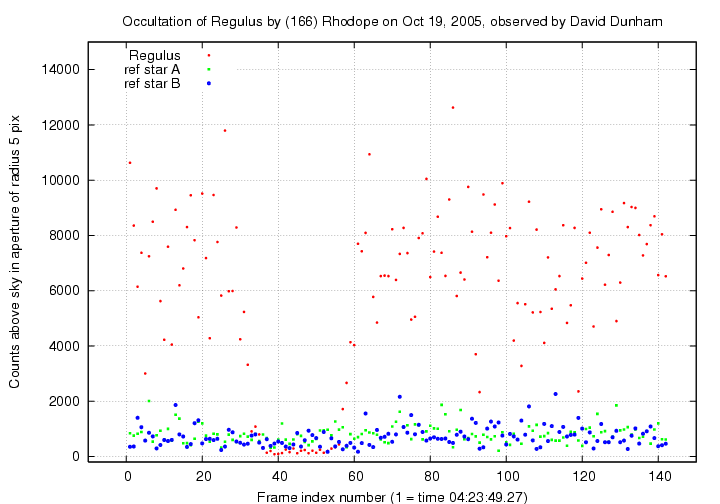
To gauge the precision of the photometry, I calculated the mean flux and standard deviation from the mean for each star over two sections of the record (both of which are outside the occultation).
star mean counts standard deviation
-------------------------------------------------------------------
frames 1-20
Regulus 7104 2062
star B 867 413
star C 762 427
frames 70-100
Regulus 7474 2067
star B 938 390
star C 884 388
--------------------------------------------------------------------
The precision of the photometry is low. This is not surprising: if one watches the video file as a movie, the stars twinkle strongly.
Scintillation noise can be important when one uses a small aperture and short exposure times. Let's do a quick calculation to estimate the size of variations due to scintillation. The paper Atmospheric Intensity Scintillation of Stars. III. Effects for Different Telescope Apertures by Dravins et al., PASP 110, 610 (1998) provides a rough guide:
-0.67 1.75 -0.5
sig = 0.09 * (D) * (sec Z) * exp(-h/h0) * (2T)
in which
Plugging in all these values, we end up with an estimated scintillation noise of about sig = 0.43, which means that the variations in the signal are expected to be about 43 percent of the signal. Looking at the statistics of the faint stars B and C, that seems about right. The scatter in the light of Regulus is a bit smaller than this figure; perhaps that is due to some small non-linearity in the signal, since the peak pixels were close to saturation in the digitized frames.
Here are quick views of the results.
The entire light curve:
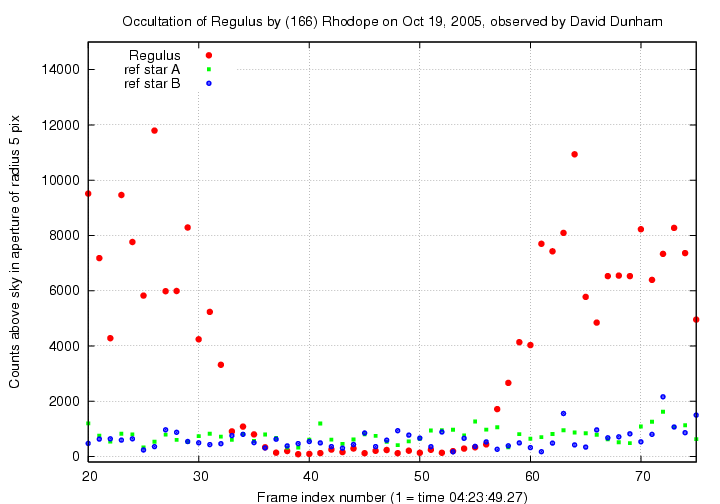
A closeup around the occultation:
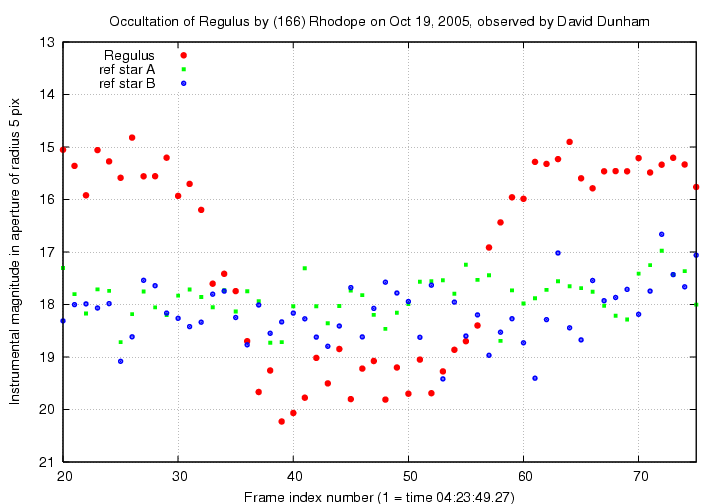
The same set of frames, but with intensity converted into logarithmic units (instrumental magnitudes):
You can grab the data in a multi-column ASCII text file below. The columns are
col quantity
------------------------------
1 frame index
2,3 flux of Regulus in 4-pixel-radius aperture,
and estimate of uncertainty in that flux
4,5 ditto 5-pixel aperture
6,7 ditto 6-pixel aperture
8,9 ditto 7-pixel aperture
10,11 ditto 8-pixel aperture
12,13 flux of star B in 4-pixel aperture,
and estimate of uncertainty in that flux
14,15 ditto 5-pixel aperture
16,17 ditto 6-pixel aperture
18,19 ditto 7-pixel aperture
20,21 ditto 8-pixel aperture
22,23 flux of star C in 4-pixel aperture,
and estimate of uncertainty in that flux
24,25 ditto 5-pixel aperture
26,27 ditto 6-pixel aperture
28,29 ditto 7-pixel aperture
30,31 ditto 8-pixel aperture
What can we learn from this event? There are two main possibilities:

On the ground, an observer measures T, the duration of the occultation. That is related to the transverse component V of the asteroid's velocity relative to the Earth, and the projected diameter d of a chord through the asteroid, like so:
d
T = ------
V
So, if we know V and measure T, we can compute the projected diameter of this particular chord of the asteroid:
d = T * V
How long is the occultation? I'll pick the times at which the light from Regulus dropped to half of its normal level (as you will see later, this makes more sense for a marginally resolved stellar disk than the figure of three-quarters of the normal flux sometimes used for an unresolved disk). These are
The duration of the occultation is thus (59 - 32) = 27 +/- 2 frames. At a frame rate of 30.03 frames per second, this is T = 0.899 +/- 0.067 seconds.
How does this compare to the values derived by David Dunham in his report? He measures a flux at the 50% level starting at 50.25 +/- 0.05, and ending at 51.20 +/- 0.05 seconds. That makes a duration of 0.95 +/- 0.10 seconds, which is entirely consistent with the my value.
How can we figure out the transverse component of the asteroid's motion relative to the Earth? If we wanted to do it from scratch, we'd have to compute the Earth's position and velocity in the Solar System near the time of occultation, and the asteroid's position and velocity as well. We can get a rough idea from NASA's Near Earth Object Program "Orbit Diagram" page
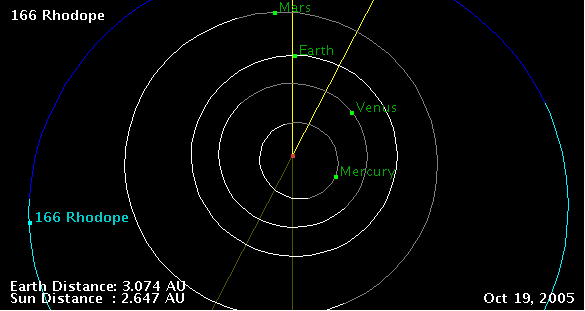
Rhodope is not far from quadrature, which means a fair fraction of its motion relative to Earth will be radial, rather than across the plane of the sky. That means that this particular occultation will last a bit longer than one near opposition.
However, we can skip all the tough calculations by going to the JPL Horizons ephemeris system and letting it do the work. We find that on UT Oct 19, 2005,
The apparent transverse component of the velocity of Rhodope relative to Regulus would then be
V = L * w
= (4.596E11 m) * (6.95E-8 radians/s)
= 31940 m/s
And we can now compute the projected length of this chord of Rhodope:
d = T * V
= (0.899 +/- 0.067 s) * (31940 m/s)
= 28700 +/- 2100 m
= 28.7 +/- 2.1 km
How does this compare to values quoted in David Dunham's report? That report contains this statement:... Then fitting the other reports (sometimes as much as 2.55 seconds), one finds an ellipse 45.9+/-0.5km (width) by 63.4+/-0.4km (length) ...These figures are consistent with my estimate as long as none of the other observations ran through the very center of the shadow. I can't find additional information on them at the moment, so I'll move on.
Now, the other item we can try to learn from this event is the apparent angular size of the star Regulus. How do we do that?
The answer is: it depends. If the angular size of the star is big enough, then one will see a gradual decrease in its light as the asteroid gradually covers the disk. On the other hand, if the angular size of the star is small, then the flux from the star will oscillate as the leading (or trailing) edge of the asteroid covers (or uncovers) it. You can read about these effects in a document describing diffraction effects during a lunar occultation.
For practice, let's compute some of the factors which go into the mix. The parameter b describes the spacing between diffraction fringes projected onto the Earth's surface (if it is perpendicular to the line of sight of the occultation). This parameter is
b = sqrt ( L * lambda )
where
With these choices, we find the fringe spacing would be roughly b = 500 m if the surface of the Earth were perpendicular to the line of sight to the star and asteroid.
Recall that the linear speed of the shadow across the Earth's surface (if it were perpendicular to the line of sight) would be about V = 31940 m/s. We would therefore predict that a characteristic time for the oscillations in the flux level due to the passing of fringes across the detector would be
b
t = -----
V
500 m
= -----------
31940 m/s
= 0.016 sec
Note that this is very roughly 1/60 of a second, about the duration of a single video field. In other words, we ought to expect that any oscillations in the flux level due to diffraction effects would be too rapid to appear in a video record -- especially one which combines two fields into a single frame of duration 1/30 second.
But ... what if Regulus were not a perfect point source of light, but an extended disk? Then the oscillating change in flux would be smeared out by the extended light distribution, and we might expect a gradual decrease in light as the leading edge of the asteroid gradually moves across the star.
What do we know about the apparent size of Regulus? We can look in the Catalogue of Stellar Diameters (CADARS) to check. I found 18 entries for Regulus, showing an average apparent angular diameter of about alpha = 1.4 milliarcseconds. Now, if we project this angle the distance L from Rhodope to Earth, we find an apparent linear size of the disk
D = L * tan(alpha)
= (4.596E11 m) * tan(0.0014 arcsec)
= 3100 m
This is much larger than the fringe spacing of b = 500 m, which means that all the diffraction effects will be smeared out. To first order, we expect to see a gradual decrease in the flux from Regulus over a timescale
D
t = ------
V
3100 m
= ------------
31940 m/s
= 0.098 seconds
= about 3 video frames of 1/30 second each
Let's look at the flux measurements again:

Indeed, what we see is a gradual decrease from the normal level of about 8000 counts over several frames, a period of very little light, and then a gradual increase back to the normal level over a period of several frames. If we wish, we may claim to have confirmed at a very rough level the angular size of Regulus.
If we wanted to do this job properly, we would have to include factors for the tilt of the Earth's surface relative to the line of sight at the location of the observer; since the measurement was made when the object was only about 27 degrees above the eastern horizon, this tilt would be significant.
We might also need to include the contribution of the Earth's rotation to the duration of the ingress and egress. Since the transverse linear speed of the asteroid across the line of sight in this case is about 32000 m/s, and the maximum possible rotational speed of the Earth (for an observer on the equator looking directly overhead) is only about 465 m/s, this rotational correction is probably insignificant for most purposes.
 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.