Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Table of contents:
Derek Breit observed this event from a location near Sun Valley Mall in Concord, California. His equipment:
12" LX200 Watec 802h Mogg Focal Reducer f6 / f3 (video is at f/3, I believe) McAFEE VTI 9" TV/VCR Combo
The start of the videotape has a GPS fix which reads:
Lat/Lon 3757.84050, N, 12203.62600, W Alt: 0021.21, M Date: 04,03,2006
Note that Walt Morgan also observed this event. You can read about his results at
I think that the event both Walt and I analyzed, a disappearance near UT 02:39:26, might correspond to the last obvious disappearance in Breit's videotape, around frame 18,460, but I can't be sure.
Derek digitized his videotape and sent me a digital movie file. Each frame was 720 x 480 pixels in size. I checked the timestamps: the times below are approximate, based on the blurred superposition of stamps from two fields into a single frame.
frame index UT time ------------------------------ 9000 02:34:14.50 24000 02:42:35.02 ------------------------------
This yields a rate of 29.969 frames per second, close enough to perfect video rate to make me believe that no frames were dropped.
A sample image from the video is shown below: number 9000. Note that one can see dimly the portion of the Moon which is lit only by earthshine.
Over the course of the videotape, the amount of sunlit Moon grows as the field drifts slightly. That extra light caused the videocamera's gain to drop, making the darker portion of the Moon pure black. Here is frame 18,000:
The only star visible in any of the frames is the target star, HD 14688. Since the star is sometimes invisible, and often very faint, I needed some other sources of signal to serve as markers. I chose two features on the sunlit limb of the Moon near the cusp, which I call the "mountain" and the "hill".
I will use the "mountain" as the primary reference, since it appears clearly in all frames. The "hill" serves as a secondary reference; it has roughly the same brightness as the unocculted target star.
Over the course of the videotape, the Moon drifts slowly across the field of view; and, at the same time, the target star drifts slowly with respect to the Moon. To simplify things, I created a coordinate system with the "mountain" at the origin. In this coordinate system, the "hill" is always at a fixed position, while the target star moves gradually downwards, scraping the limb.
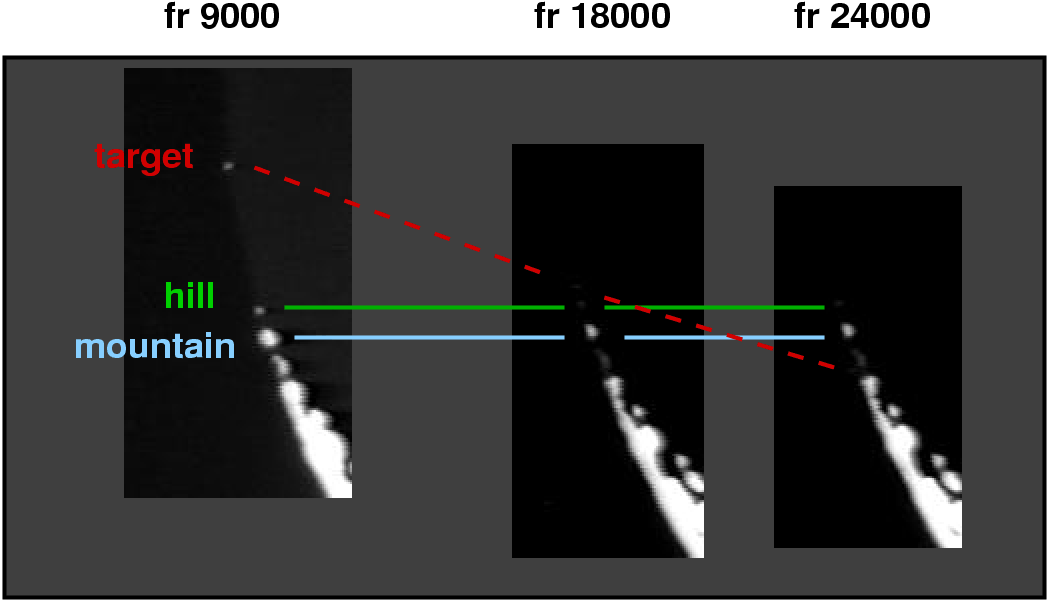
Using a set of 5 frames spaced widely across the interval from frame 9,000 (when the target star becomes very close to the limb) to frame 20,000 (when the target star is between "hill" and "mountain"), I determined a linear fit to the position of the star as a function of frame index. My plan was then to analyze each frame in the following manner:
Near the end of the sequence, the computed position of the target star happens to lie very close to the position of the hill, and, later, the mountain. At these times, the measurements of target star light will be contaminated and difficult to interpret.
First, I broke the video clip into individual frames using mplayer. The result was a set of roughly 25,000 JPEG images, each 720 x 480 pixels in size. I next
The only star visible in the frames is HD 14688 itself. Some information on the star, taken from SIMBAD
HD 14688 = HIP 11075 = GSC 1215-0971
B=6.93 V=6.97 spectral type A2V
spectroscopic binary with period 4.32 days
RA = 02:22:33.20 Dec = +16:52:13.0
The FITS images showed that the peak pixel values were, at the start of the section of interest (frame 9000), about 220, 130, 110 for mountain, hill, target, respectively; and, near the end of the section (frame 20,000), about 170, 20, 20, respectively. The hill and target star were definitely not saturated. The FWHM appeared to be about 3.5 pixels at the start, and shrank to about 3.0 pixels after the gain changed.
For each of the frames, I
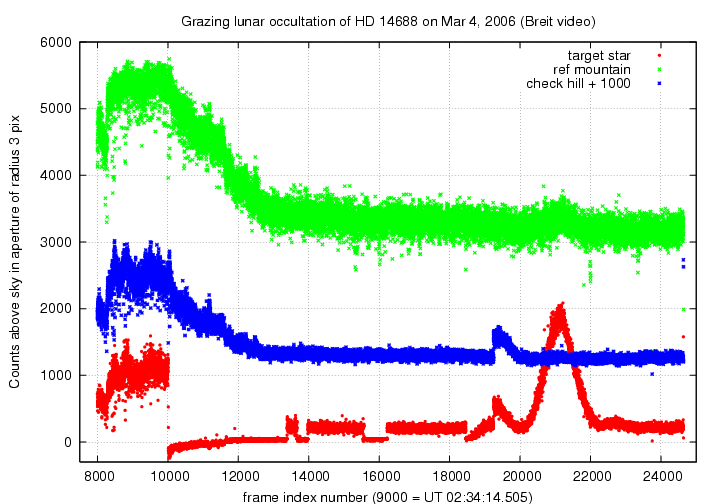
I decided to use the aperture of radius 3 pixels for the plots below.
The entire light curve, using an aperture radius of 3 pixels. Note the following:
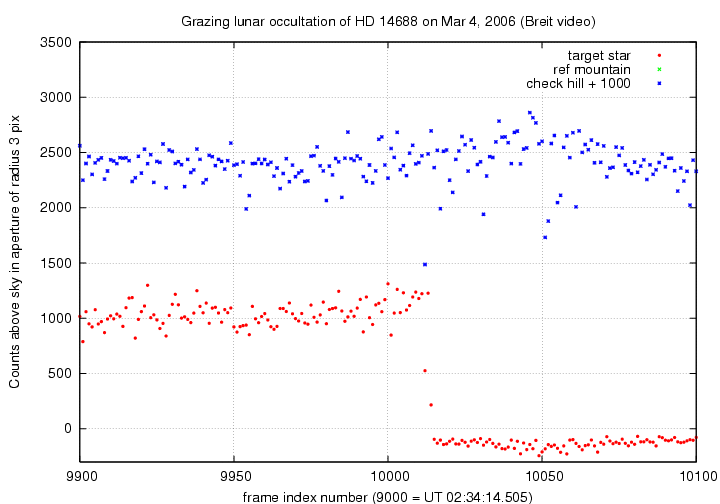
A closeup of the first disappearance:
A closeup of first re-appearance, then second disappearance and re-appearance:
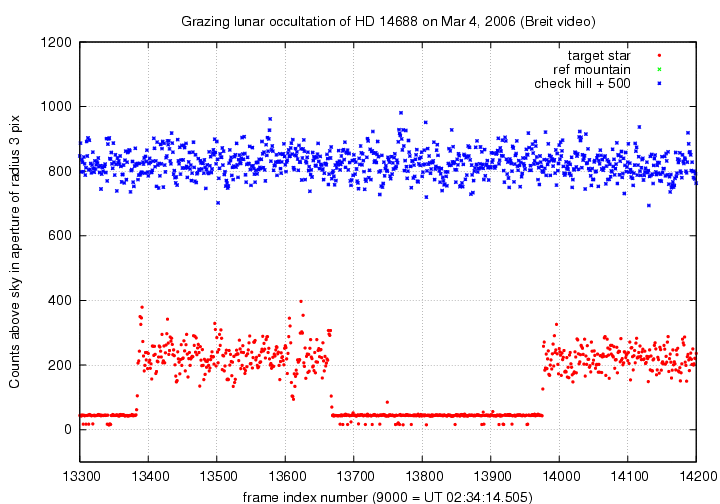
Derek suggests that there may be an event from about frame 13609 to 13621: a short, partial dip with a somewhat gradual recovery. I don't think that my photometry alone is sufficient evidence for the event; this is an instance where frame-by-frame visual analysis is needed.
A closeup of third disappearance and re-appearance:
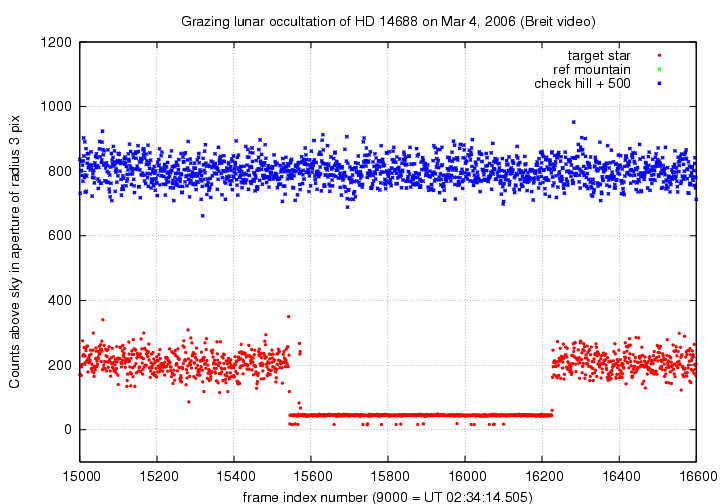
If you look very closely around frame 15560, you can see a very brief "flash" which lasts only a few frames. Thanks to Derek for noticing this brief event.
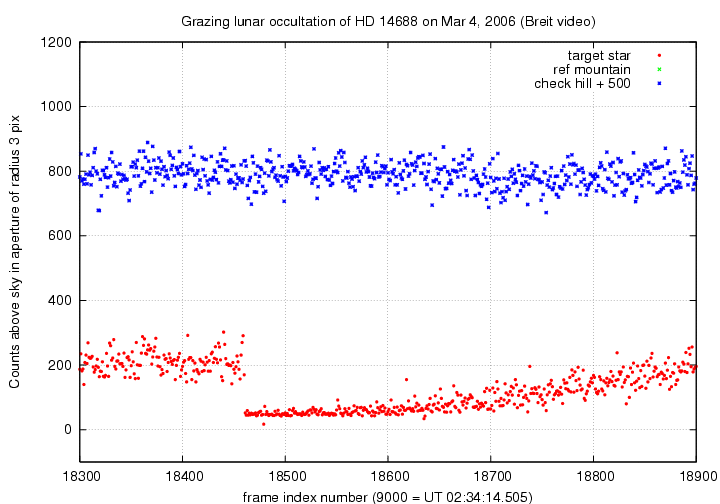
A closeup of what appears to be -- but is not! -- a gradual reappearance as the target star approaches the hill. What is really happening is that the target is completely hidden, but a larger and larger amount of the hill's light is falling into the target's aperture. Remember, I am moving the target's aperture to its approximate position, and measuring all light which falls into it. This section of the light curve might be studied better by visual inspection of the videotape, frame-by-frame.
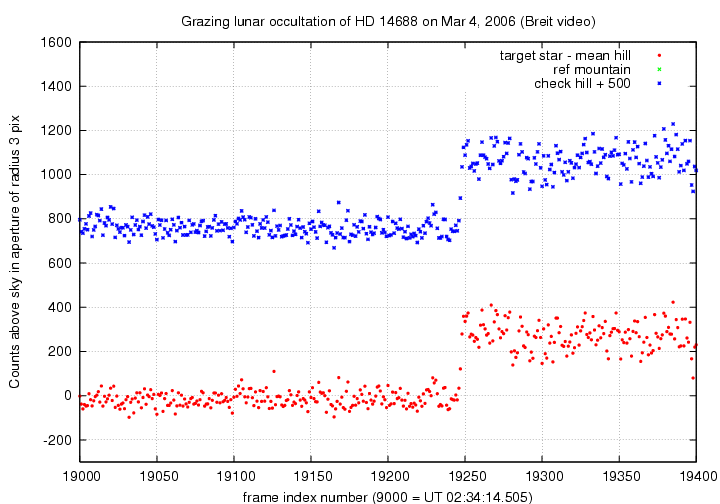
A larger view of the target's position merging with the hill, and then merging with the mountain. Note how the hill's light does not increase -- due to any extra flux from the superimposed target star -- until about frame 19,250. That sudden jump marks the real re-appearance of the target from behind the limb.
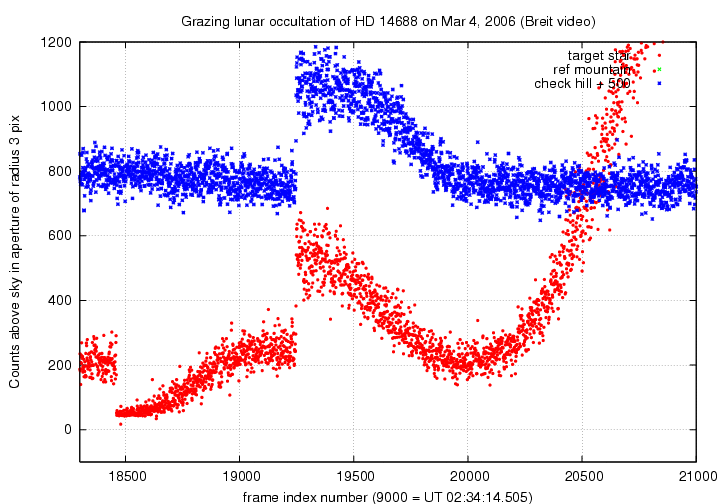
Here's a closeup of that section of the record, at which the target star suddenly re-appears while at the same position as the hill. I have measured the hill's average light both before (frames 19,000 - 19,200) and after (frames 20,000 - 20,200) this event, computed the mean value (262 counts +/- 36 counts), and subtracted that mean value from the light in the target's aperture.
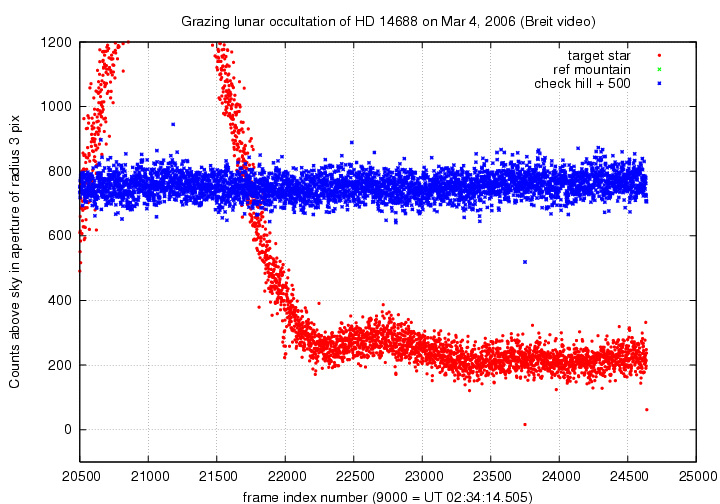
The final section of the video record, as the target star leaves the region of the mountain and creeps along the limb. I don't think there is any significant information here.
You can grab the data in a multi-column ASCII text file below. The columns are
col quantity
------------------------------
1 frame index
2,3 flux of mountain in 2.5-pixel-radius aperture,
and estimate of uncertainty in that flux
4,5 ditto 3-pixel aperture
6,7 ditto 3.5-pixel aperture
8,9 flux of hill in 2.5-pixel-radius aperture,
and estimate of uncertainty in that flux
10,11 ditto 3-pixel aperture
12,13 ditto 3.5-pixel aperture
14,15 flux of target star in 2.5-pixel-radius aperture,
and estimate of uncertainty in that flux
16,17 ditto 3-pixel aperture
18,19 ditto 3.5-pixel aperture
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.