The linear weights method of measuring the offensive contribution of Major League baseball players is arguably the most accurate assessment tool available. The metric was created by Pete Palmer, and has been expanded and advanced through the further research of people like Mitchell Lichtman, Tom Tango, Andrew Dolphin, Dave Studeman, and many more. The following article, and the resultant data, borrows liberally from these innovative men.
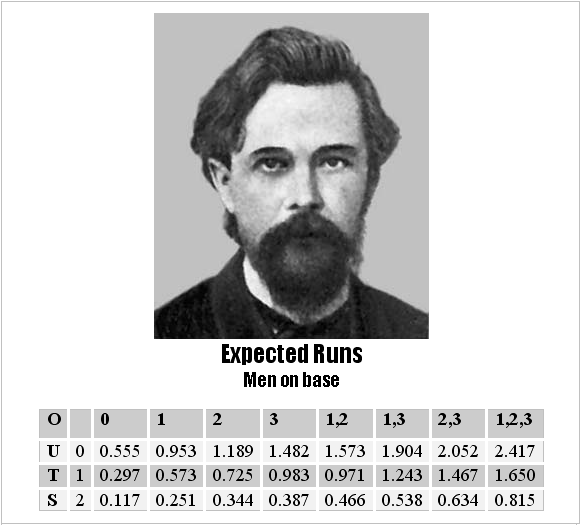
Baseball is Markovian in nature in that what happens in an at bat is dependent on past events, just as future events are influenced by present events. A single with two outs and no runners on base has a different value than a single with the bases loaded and no outs, with the events leading up to those respective singles being the difference, and the subsequent events also influencing the total run result. So how does one determine with any degree of accuracy the "value" of a single (or the result of any at bat)? The following chart will help answer that question. This chart gives the “net expected run value” for each of the twenty-four different situations a batter can see in an at bat, from none on, none out, to bases loaded, two outs. The run values are calculated by looking at each at bat in major league baseball over the course of multiple seasons with similar run environments and determining how many runs score subsequent to each of the situations. These totals are then averaged to give the "net expected run values" for each situation. This may be easier to understand when looking at the first batter of an inning – with no outs and none on, an average team will score 0.555 runs. Multiplying this by 9 innings in a game yields 5 runs, which is the approximately average number of runs scored by American League teams last season (and also what an average National League team would score if you replaced the pitcher's at bats with an "average" player), thus with no outs and none on, an average team will score 0.555 runs.

Looking at the chart, one can see that with a man on first and one out an average team (that scored the league average number of runs) would be expected to score 0.573 runs. If the batter coming up in that situation doubles, and the run scores, he has influenced the game by +1.00 for the run that scored and +0.152 for the difference between the resulting runner on 2nd with one out (0.725) and the former runner on first with one out (0.573), for a total contribution of +1.152 runs. Conversely, if the batter popped out he would have contributed –0.322 runs, the difference between the situation he inherited and the one he left. (If you're not familiar with this chart, take a few minutes and play with the situations – it's really pretty cool and shows clearly that “productive outs” are not really all that productive.)
One way of assessing a player's offensive contribution would be to go through each of their at bats individually over the course of a season and, based on the situation they inherited and how their at bat affected it, calculate the net results of their contributions. If you were to do this for every non-pitcher in baseball and total the results, you would logically have a total sum of zero runs, as all these players together make up the MLB average sans pitchers. Besides being incredibly work intensive, this method of assessing offense can be somewhat misleading because of the opportunity issue, i.e., a player coming to bat after two batters with .400 OBP's could have an advantage over a player batting after weak hitters. So what else can we do?
I like using the following method, which takes the average of all the batting results over the course of a season, i.e., the average contribution of all singles, doubles, fly balls, etc, and finds a value for each of those specific results. For example, if you took the total run contribution (from the chart) of every single over the course of an entire season in Major League Baseball, and divided it by the total number of singles, you would have the average value of a single. This will work for any batting result, and the total sum of all the batting results used should equal zero. The tricky thing here is how detailed you want to get in your breakdown. Do you want to know the value of all ground balls, or do you want to break them down by ground balls to each position? I will leave the level of breakdown to you for your future forays into this type of assessment, but will say that a simple breakdown yields very similar results to a more detailed one, and is much less labor intensive. What I have done for the 2007 season is use the average value of eleven batting results to determine the offensive contribution in runs above or below average for every player with over 350 plate appearances. Because of the disparity in league talent level, I used separate values for the American and National Leagues. The values I used were as follows:
American League National League ------------------------------------------------------------- Singles 0.480 Singles 0.480 Doubles 0.770 Doubles 0.770 Triples 1.070 Triples 1.070 Home Runs 1.400 Home Runs 1.400 Walks/HBP 0.320 Walks/HBP 0.320 Intentional Walks 0.185 Intentional Walks 0.185 Strikeouts -0.284 Strikeouts -0.292 Groundouts -0.303 Groundouts -0.312 Fly Outs -0.269 Fly Outs -0.278 Stolen Bases 0.193 Stolen Bases 0.193 Caught Stealing -0.437 Caught Stealing -0.437 -------------------------------------------------------------
Applying these values to the total offensive statistics for all for all non-pitchers in baseball in 2007 for each league yields net results of zero, meaning these average numbers "work."
The following datafiles list traditional statistics for each player with over 350 plate appearances, along with the player’s total Linear Weights contribution, and their LWTS contribution per 603 PA. The data is sorted by position, and includes the average stats per 603 PA for that position.