Table of contents
Everyone knows that Joe Dimaggio holds the record for longest streak of consecutive games with a hit: 56. The number is one of the few, like 60 and 714 (neither of which is a record any longer ...), that has made its way into popular culture. For example, biologist Steven Jay Gould devoted one of his "Natural History" columns to the feat to illustrate a discussion of probability.
No one has broken this record, or even come close to it, since it was set in 1941. Why not? Is this some sort of "Super Outlier", a one-in-a-million event that will stand forever? Or is there some reasonable chance that a player will break this record in the next decade?
I decided to investigate the phenomenon of consecutive game hitting streaks in a statistical manner. One of my goals is to figure out if baseball players may be modelled accurately by dice or coins or random number generators, or if their behavior does not match that of a truly random system. Baseball players, like all people, have good days and bad days; they stub their toes, catch colds, eat a little too much occasionally. Should such minor inconveniences cause their behavior to deviate from that of an inhuman, unchanging die?
Let's see what we can see.
I will analyze the actual hitting streaks of Major League Baseball players from 1954 to 2008. Why that range? Because the excellent Project Retrosheet provides free access to play-by-play records of baseball games starting in 1954. Alas, this range doesn't cover the crucial year, 1941, when Dimaggio hit in 56 straight games (and Ted Williams batted 0.406), but so it goes.
The Retrosheet data allows me to examine each batter's actions during an entire season, every plate appearance in every game. For example, Luis Castillo played for the Florida Marlins in 2002. In his first game, he came to bat five times, with the following results:
| Retrosheet code | result |
| play,1,0,castl001,12,FBFX,S7/7S | single to left field |
| play,3,0,castl001,11,CBX,3/G | ground out to first base unassisted |
| play,5,0,castl001,00,X,6/P6 | pop up to shortstop |
| play,7,0,castl001,32,BBCBCX,S.2-3;1-2 | single (advancing runners to second and third) |
| play,9,0,castl001,12,LLBFFC,K/C | strikeout |
It's important to know exactly what happened during each plate appearance, because the rules for a consecutive game hitting streak are a bit complicated. From the MLB Rule Book, section 10.23:
CONSECUTIVE-GAME HITTING STREAKS. A consecutive-game hitting streak shall not be terminated if all of a batter's plate appearances (one or more) in a game result in a base on balls, hit batsman, defensive interference or obstruction or a sacrifice bunt. The streak shall terminate if the player has a sacrifice fly and no hit. A player's individual consecutive-game hitting streak shall be determined by the consecutive games in which such player appears and is not determined by his club's games.
The Retrosheet data allows me to account for sacrifice flies, sacrifice bunts, defensive interference, and other events properly.
In addition, the Retrosheet data allows me to simulate the player's actual season more accurately than I could with a simple season-ending statistical line. Let me explain. In 2002, Castillo had 606 official at-bats and appeared in 146 games. If that was all the information I had, I might say, "Well, that's an average of 4.15 at-bats per game, so if I want to simulate his season, I'll create 146 fictional games and give him 4.15 at-bats in each one, or maybe 4 at-bats in most games and 5 in a few." However, if we look at the Retrosheet data, we can see that his actual at-bats didn't follow such a simple plan. In his first 10 games, his actual number of at-bats was
5, 4, 5, 4, 3, 4, 3, 5, 3, 1
Note that last number: in his tenth game of the season, Castillo had just one official at-bat. In that game, a 2-0 loss to the Braves on Friday, April 12, 2002, Castillo came in to pinch-hit for Alex Gonzalez in the eighth inning. In this single plate appearance, he struck out looking.
If one is following a real hitting streak, or simulating one in a computer, it's very important to know that a player had just a single chance to get a hit in some particular game.
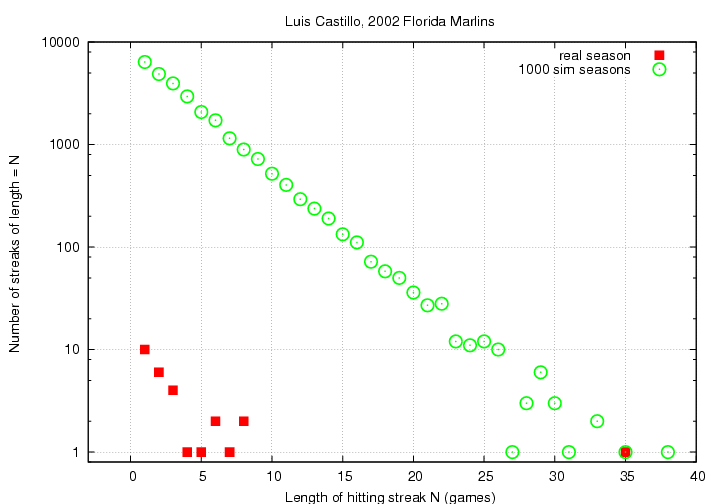
The first step is to make sure that my dataset is reasonably complete, that my ability to decode it is correct, and my algorithm for finding hitting streaks works properly. Therefore, I went through the 1954-2008 period and looked for the longest actual hitting streaks. One can find lists of these real streaks in many places -- for example, at Baseball Almanac, which lists the longest streaks in this period as
| Actual hitting streaks 1954-2008 | |||
| Year | Player | Team | Length |
| 1978 | Pete Rose | Cincinnati | 44 |
| 1987 | Paul Molitor | Milwaukee | 39 |
| 2005/2006 | Jimmy Rollins | Philadelphia | 38 |
| 2002 | Luis Castillo | Florida | 35 |
| 2006 | Chase Utley | Philadelphia | 35 |
| 1987 | Benito Santiago | San Diego | 34 |
| 1969 | Willie Davis | Los Angeles | 31 |
| 1970 | Rico Carty | Atlanta | 31 |
| 1980 | Ken Landreaux | Minnesota | 31 |
| 1999 | Vladimir Guerrero | Montreal | 31 |
I then ran my code to analyze the Project Retrosheet datafiles for this time period, and sorted the results to find the longest actual hitting streaks. Here's my list:
Year Team Player Streak
----------------------------------------
1978 CIN Pete Rose 44
1987 MIL Paul Molitor 39
2005 PHI Jimmy Rollins 36
2006 PHI Chase Utley 35
2002 FLO Luis Castillo 35
1987 SDN Benito Santiago 34
1999 MON Vladimir Guerrero 31
1980 MIN Ken Landreaux 31
1970 ATL Rico Carty 31
1969 LAN Willie Davis 31
----------------------------------------
Yes, that's the sa--- WAIT a minute. There is one difference: the official list shows Rollins' streak to be 38 games, while mine shows a length of only 36 games. The reason for the difference: my code only considers a single season at a time, while the official rules allow a streak to continue from one year to the next. Jimmy Rollins got at least one hit in his final 36 games of the 2005 season, as my code recovered, and then went 1-4 and 2-4 in his first two games of the 2006 season before ending the streak on April 6, 2006.
So, as long as we place one additional constraint on hitting streaks -- that they must begin and end during the same season -- I think that my code will do an accurate job of finding them.
One of the cruelest facets of the consecutive game hitting streak record is it unforgiving nature: just one bad game will break the streak. In addition to skill, a player needs a good deal of luck, both on and off the field, to keep a streak going. Catching a cold, cutting a finger, twisting an ankle -- any minor injury can ruin a streak. Suppose we take a kinder, more gentle view of hitting streaks, and allow a batter to have ONE BAD GAME in which he fails to get a hit.
Let's define a "broken hitting streak" to be one official consecutive game hitting streak of N games, followed by one game with no hits, followed by another official consecutive game hitting streak of M games. We'll set the length of this "broken hitting streak" to be the sum N+M. In other words, we'll just pretend that the one hitless game in the middle of the streak didn't exist.
What is the longest "broken" hitting streak during our study period, 1954 - 2008? Surely it must be much longer than any official hitting streak. Could it, in fact, be longer than Dimaggio's record of 56 games?
Well, since I had all the play-by-play data, it wasn't hard to make a small change in my software to count streaks in which a single hitless game intruded. I was hoping for a really big result, but what I found was ... a bit of a disappointment:
Strange, but true.
Pete Rose his official streak of 44 games on June 14, 1978, going 2-4 in a 3-1 win against the Cubs. If we examine his performance just before this point, we find 0-3 with a walk on June 13, 1-4 with a triple on June 12, and 0-4 on June 11 against the Pirates. So one could add just a single game to the front of his official streak. Rose ended his streak on August 1, going 0-4 with one walk in a 16-4 blowout loss to the Braves. The very next day he bounced back with a great game: a home run, a double, two singles and a stolen base to help the Reds take revenge on the Braves, 6-2. However, after one day of travelling from Atlanta back to Cincinnati, Rose went 0-4 with a sacrifice fly against the San Diego Padres. By including games after the official streak, one could again add just one game to his "broken hitting streak."
A list of the top 19 "broken hitting streaks" shows few surprises. It's rather nice to see the father-and-son pair of Felipe and Moises Alou with exactly the same length.
Year Team Player Length ------------------------------------------------ 1978 Cincinnati Pete Rose 45 (2005 Philadelphia Jimmy Rollins 44) *** see below *** 1987 Milwaukee Paul Molitor 42 1966 Pittsburgh Roberto Clemente 42 2007 Mets Moises Alou 41 1968 Atlanta Felipe Alou 41 1982 Minnesota Kent Hrbek 40 2007 Yankees Derek Jeter 39 1987 San Diegeo Benito Santiago 39 1980 Kansas City George Brett 39 2001 Seattle Ichiro Suzuki 38 1985 Boston Wade Boggs 38 1980 Texas Al Oliver 38 1959 St. Louis Ken Boyer 38 2006 Philadelphia Chase Utley 37 1998 Anaheim Garret Anderson 37 2007 Cleveland Casey Blake 36 2005 Texas Michael Young 36 2002 Florida Luis Castillo 36 1967 Cincinnati Pete Rose 36 --------------------------------------------------
The streak by Rollins, marked with a ***, was not found by my code. As mentioned earlier, Rollins official streak of 38 games was split between two seasons, and my code doesn't check for streaks which span two seasons. Therefore, it failed to find this broken streak (Rollins hit in 36 games in 2005, then 2 more in 2006 to make an official 38-game streak, went hitless once, then hit in 6 more games to make a 44-game broken streak). There may be additional long broken streaks which span two seasons; if you discover one, please let me know.
Joe Dimaggio's streak of 56 games stands all by itself; the second-longest streak is only 45 games (Wee Willie Keeler, 1896/1897). Some people conclude that Dimaggio's feat is so far from the ordinary, so much longer than any other streak in history, that it is hard to explain. "If we calculate the chances that even a good hitter might get a hit in 56 consecutive games," they say, "we end up with a probability so small that it might never happen again in our lifetime ... or in a thousand years." Is that right? Can we reasonably expect not to see another 56-game streak in our lifetime?
One way to answer the question, "Was Dimaggio's streak utterly improbable?" is to generate a large number of simulated seasons for other players, as accurately as possible, and look to see how many simulated streaks reach 56 games. Let me describe my method for simulating player performance, and then tell you about my results.
First, for each player in MLB, and for each season between 1954 and 2008, I made a list of the number of streak-at-bats (SABs) in each game in which he appeared.
What's a streak-at-bat? It's almost the same as an official at-bat, except for sacrifice flies. Under the official baseball rules, a batter who hits a sacrifice fly is not given an at-bat. However, under those same rules, a sacrifice fly MAY act to end a consecutive-game hitting streak. Therefore, in order to simulate hitting streaks properly, I will count all plate appearances in which a batter hits a sacrifice fly as "streak-at-bats", and I'll include those appearances in my simulations as chances for the batter to make a hit or be put out.
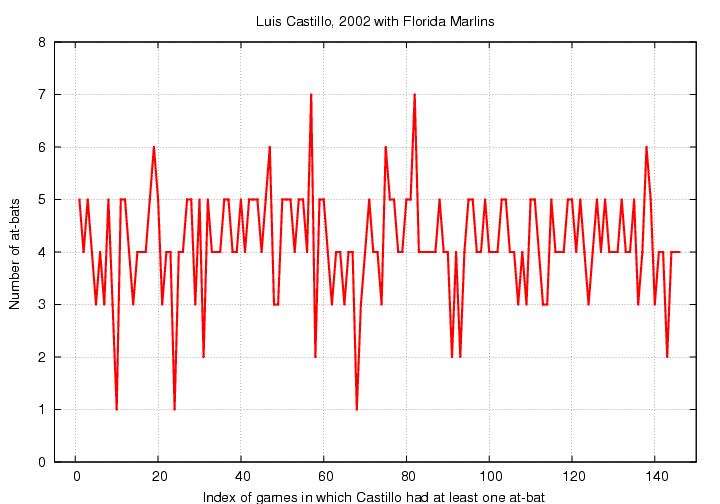
Let me continue to use Luis Castillo's 2002 season with the Marlins as an example. He had at least one streak-at-bat (SAB) in 146 games that season. Rather than listing the number of SABs in these games, let me show you in a graph.

Notice that there are 3 games in which Castillo had only a single at-bat, and 2 games in which he had 7 SABs. Accounting for these unusual games could be very important for the survival of a hitting streak.
My next step was to compute the streak-batting-average (SBA) for the player over the entire season. Castillo had 607 SABs and 185 hits, yielding a SBA of 0.305.
Now, the main part of the simulation. I went through each game that Castillo played during the 2002 season, one at a time. During each game, Castillo had a known number of SABs. For each SAB, I used a random-number generator (the gsl_rng_uniform routine from the GNU Scientific Library , if you must know) to create a value between 0.0 and 1.0. If the value was less than or equal to the player's SBA, then the player was deemed to get a hit; otherwise, the player was deemed to make an out. I kept track of the number of SABs and hits for the batter in each game.
That gave me one simulated season for the player. I then examined the record of SABs and hits for each game to search for consecutive-game hitting streaks, just as I had done earlier with actual game records from Project Retrosheet. I made a list of the number of hitting streaks of 1 game, 2 games, 3 games, ..., up to the longest hitting streak in the entire simulated season. For Castillo in 2002, one simulated season yielded
Length Number of streaks ------------------------------ 1 6 2 7 3 4 4 5 5 2 6 2 7 1 8 0 9 1 10 0 11 0 12 0 13 0 14 0 15 0 16 0 17 1 --------------------------
Recall that Castillo had a REAL streak of 35 games during this season. Well, it's not surprising that a single simulated season doesn't have any streak of that length; the real Luis Castillo doesn't have any other seasons with hitting streaks that long, either. In fact, Castillo's second-longest real streak is 22 games, set in 1999.
But why stop with a single simulated season? We can generate as many random numbers as we like. I therefore chose to generate 1000 simulated seasons for each real season of each player's career. I analyzed each simulated season as described above, and built up a table showing the number of hitting streaks of 1 game, 2 games, 3 games, ..., over all 1000 simulated seasons.
For Luis Castillo, in his 2002 season, the final table of simulated hitting streaks looks like this:
Length Number of streaks
------------------------------
1 6387
2 4879
3 3947
4 2945
5 2077
6 1723
7 1150
8 894
9 722
10 519
11 404
12 293
13 237
14 190
15 133
16 111
17 72
18 58
19 50
20 36
21 27
22 28
23 12
24 11
25 12
26 10
27 1
28 3
29 6
30 3
31 1
32 0
33 2
34 0
35 1
36 0
37 0
38 1
--------------------------
The longest of all these simulated streaks is 38 games, and there is a 35-game streak as well. So, we might very very roughly conclude that the chances that Luis Castillo has a 35-game hitting streak, given his performance and schedule of appearances in 2002, is about two out of one thousand (2/1000 = 0.002 = 0.2 percent).
Is the distribution of simulated streaks similar to the distribution of real streaks? A straight comparison is somewhat difficult, since the numbers of simulated streaks are so much larger:
Let me normalize the list of simulated streaks, dividing the number of streaks by 1000 to bring the numbers back into the range expected for a single season. As you can see, the real and simulated distributions are not very different in their small region of overlap.

This representation emphasizes the degree to which the long 35-game actual streak is an "outlier," doesn't it?
So, just what were the longest hitting streaks in the simulated seasons? Did any match Dimaggio's record of 56 games? The answer is ... yes. Here's a list of all instances of simulated streaks greater than or equal to 56 games in length:
Year Team Player Longest Longest
Actual Simulated
-----------------------------------------------------------
1959 MIL Hank Aaron 21 70
1980 CLE Miguel Dilone 15 68
1970 CIN Pete Rose 13 66
1956 DET Harvey Kuenn 10 65
2008 CHN Derrek Lee 10 64
1961 PIT Roberto Clemente 13 64
1954 NYG Don Mueller 21 63
2000 NYY Derek Jeter 13 61
2007 SEA Ichiro Suzuki 25 60
1993 COL Andres Galarraga 15 59
2001 COL Juan Pierre 12 58
2000 MON Jose Vidro 14 58
2000 ANA Darin Erstad 11 58
2008 WAS Christian Guzman 14 57
2006 NYY Derek Jeter 25 57
2001 SEA Ichiro Suzuki 23 57
1996 COL Eric Young 17 57
1971 ATL Ralph Garr 21 57
2007 PHI Chase Utley 19 56
2004 SEA Ichiro Suzuki 21 56
2004 SEA Ichiro Suzuki 21 56
1979 KCA George Brett 13 56
1974 ATL Ralph Garr 14 56
-----------------------------------------------------------
(No, that's a not a mistake: Suzuki had two separate simulated versions of his 2004 season in which he achieved 56-game hitting streaks, so I'm listing it twice)
This is quite a mix of familiar and expected names -- Suzuki, Jeter, Rose, Aaron -- and obscure (to me) ones -- Garr, Dilone, Kuenn. Let me just mention a few facts about these latter three in particular, since I looked up their entries after seeing them on this list. Miguel Dilone played outfield between 1974 and 1985 for eight different teams. His best year by far was 1980, when he batted 0.341 and slugged 0.432 for the Cleveland Indians. He ended up twenty-second in the MVP voting that year. Harvey Kuenn started out playing shortstop for the Tigers in 1952, switching to outfield later in his career. He moved to the Indians in 1960 for a few years, then ended his career with the San Francisco Giants. He won Rookie of the Year in 1953 and finished in the top ten of MVP twice: in 1956, the year in which one of his simulations reached a 65-game hitting streak, and in 1959, which was slightly better by most rate statistics. Ralph Garr, an outfielder, played between 1969 and 1980 for the Braves, White Sox and Angels. He made the All-Star Team in 1974.
I think it's pretty clear from this list of names that long consecutive-game hitting streaks are not the province of what we usually consider to be great hitters. Yes, a few great hitters do appear on this list, but most are decent players who had three skills:
That last item is pretty important. Walks are, from a general offensive standpoint, very good. However, they represent missed opportunities to get a hit; since a typical player comes to the plate only 4 or 5 times per game, even a single walk reduces his chances of getting a hit in the game substantially. A player who is consciously attempting to maintain a long hitting streak will very likely do harm to his team's chances of winning by swinging at some pitches which are outside the strike zone.
Many people have pointed out that the consecutive game hitting streak record is in some ways more a mark of luck than it is of "proper" offensive performance. I think that's right: it's clear that a player be very skilled to hit safely in many consecutive games, but the skills needed to do so aren't necessarily the ones that will help one's team to win games.
Let me begin by writing that I don't think there is any one definitively correct answer to this question. There are several different avenues one can take to address it, and each one provides a different view. The best we can do, I think, is to examine the results of those several methods together.
In general, during the following discussion, I will tend to treat the entire period from 1954 to 2008 as a single unit, during which no significant change occurs. This is, of course, patently wrong, since
One very simple way to estimate the chances that a hitter might match or break Dimaggio's record is to look at the results of all the simulated seasons for all the players on all the teams from 1954 to 2008. There were a total of 23 simulated seasons in which a player had a streak of at least 56 games. One can view my simulations as providing 1000 different possible instances of this entire stretch of time. In only 23 of those instances did a streak reach 56 games. Therefore, one might conclude that
A. the chance of a 56-game hitting streak occurring at least once in the MLB over a 55-season period is 23/1000 = 0.0023 = 0.23 percent.
That duration of 55 seasons is not far from a reasonable lifetime of watching baseball. One could rephrase this result to write, "The chances that you'll see someone have a hitting streak of 56 games or longer during your lifetime is about one quarter of one percent."
We can use that result to estimate the chances that a 56-game hitting streak will happen during any single season:
B. the chance of a 56-game hitting streak occurring in a single MLB season is 0.0023/55 = 0.000046 = 0.0046 percent.
Building on these results, we can ask, "How long must one wait to see a hitting streak of at least 56 games?" Suppose that we want at least a 50-percent chance of seeing such a streak. If the probability of some event occurring each year is 0.0 < P < 1.0, then the probability that the event does NOT occur is (1 - P). Now, let's watch for a number of years. If these events are independent (see note below), then the chances that the event does NOT occur after two years is
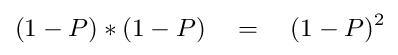
or, more generally, the probability that the event does NOT occur after N years is
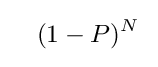
In our case, P = 0.000046. We want to know how many years N must pass before the probability that a hitter does NOT have a streak at least 56 games long rises to 50 percent. In other words, we want to solve the equation
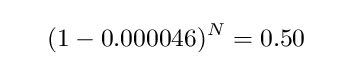
With the help of logarithms, we find N = 15,000 years, give or take a few. If we work with blocks of 55 seasons, rather then one season at a time, the timespan is closer to 16,000 years. Either way, it's a very long time.
This sort of statistical calculation makes an assumption, mentioned above, that may not be true. Each season is assumed to be statistically independent, and assumed to have the same chance of hosting a 56-game hitting streak. But that's clearly NOT true, both for the reasons mentioned earlier (more teams, more players, longer seasons as time goes on), and also because some players are much better at having long hiting streaks than others. Ichiro Suzuki, for example, has traits that make him very good at hitting streaks: he often leads off, plays almost every game, has a high batting average, and walks infrequently (about 46 times per season, or once every 16 plate appearances). A baseball season which includes a batter like Ichiro in his prime is much more likely to yield a 56-game hitting stream than a season without such a specialist.
Let's follow this thought, and examine the performance of individual players to estimate the likelihood of another 56-game hitting streak. In order to identify promising batters, I'll pick out all the simulations in which a player had a hitting streak of more than 45 games (why not 56 games? Because each player aside from Ichiro appears only once on that list. A single long streak might be due to lucky rolls of the dice; we need many long streaks to label a player confidently as "good at long hitting streaks"). There were 359 such simulated seasons. Which players appear most frequently in this list?
Multiple simulated seasons with streaks of at least 45 games
Player Number of sim seasons Number of seasons
with streak >= 45 games in MLB (1954-2008)
-------------------------------------------------------------------
Ichiro Suzuki 22 8 (+ active)
Tony Gwynn 16 20
Paul Molitor 10 21
Wade Boggs 10 18
George Brett 8 21
Kirby Puckett 7 12
Derek Jeter 7 14 (+ active)
Ralph Garr 7 13
Darin Erstad 7 13 (+ active)
Rod Carew 7 19
Kenny Lofton 6 17
Nomar Garciaparra 6 13 (+ active)
Johnny Damon 6 14 (+ active)
Michael Young 5 9 (+ active)
Bernie Williams 5 16
Shannon Stewart 5 14
Pete Rose 5 24
Harvey Kuenn 5 15
Roberto Clemente 5 18
--------------------------------------------------------------
Golly. Ichiro Suzuki stands out in this field. Even though he's only played 8 seasons in MLB, he has by far the largest number of long hitting streaks in my simulations. Let's focus on him.
Ichiro's eight real seasons turned into 8000 simulated seasons in my study. Given those 8000 opportunities, he accumulated 22 streaks of at least 45 games. All the other players with at least 10 simulated streaks had many more opportunities; Tony Gwynn, for example, generated 16 long hitting streaks in 20,000 simulated seasons. On a season-by-season basis, Ichiro is (or was) by far the most likely player to build a long hitting streak.
You may recall (from this earlier section) that Ichiro had 4 simulated streaks of at least 56 games. Since I generated 8000 simulated seasons from his 8 real seasons, we can calculate the chance that he might have a 56-game hitting streak during any one season, roughly, to be
P = 4 / 8000 = 1 / 2000 = 0.0005 = 0.05 percent
We can use this as another means to estimate the period until someone breaks Dimaggio's record. Let's assume that Ichiro represents a player with the best possible combination of skills for creating long hitting streaks.
C. the chance that the "Most Streak-Worthy" player has a 56-game hitting streak in a single MLB season is 1 / 2000 = 0.0005 = 0.05 percent
Of course, that player might compete for a number of seasons, which would raise the overall chances for him to reach the record. Suppose this player is able to play for N seasons at the same level of skill. Then the chances that he could reach Dimaggio's mark at some point during his career can be calculated as we did earlier.
D. the chance that the "Most Streak-Worthy" player has a 56-game hitting
streak at some point during his career is
if he plays N seasons probability of streak >= 56 games
-------------------------------------------------------------------
1 0.05 percent
2 0.10 percent
5 0.25 percent
10 0.50 percent
15 0.75 percent
20 1.00 percent
-------------------------------------------------------------------
It seems unlikely to me that any player can maintain the required elements -- everyday play, high batting average -- over an entire career of twenty years. Therefore, we might conclude that even the Most Streak-Worthy player has less than a one percent chance to reach Dimaggio's mark during his entire career.
You are very likely familiar with hitting streaks, but what do you know about exponential functions? Let me provide a brief introduction to them now, so that the pretty little graph I'll show later might make more sense.
An exponential function is simply one particular type of mathematical relationship between two quantities. For example, suppose that I flip a fair coin once. The chance that it lands heads-up (H) is 1/2, or 50 percent. If I flip it twice, the chance that it lands heads-up both times (HH) is (1/2)*(1/2) = 1/4, or 25 percent. What if I flip it N times? The chance that I get heads every time is given by the product of N consecutive factors of (1/2); in other words, (1/2) raised to the power of N:
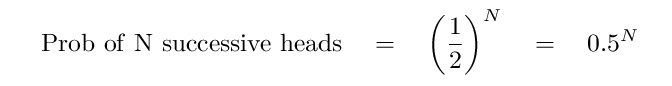
If we plot this probability as function of the number of coin flips, we see a curve which quickly drops towards zero:
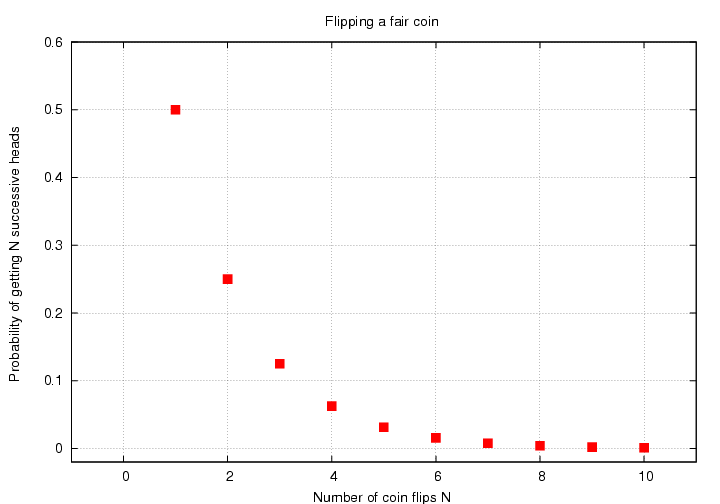
However, if we use a logarithmic scale on the vertical axis for this graph, we see a very different shape: a straight line. The slope of this line is equal to the base of the exponential function: 1/2 = 0.5, in our case.
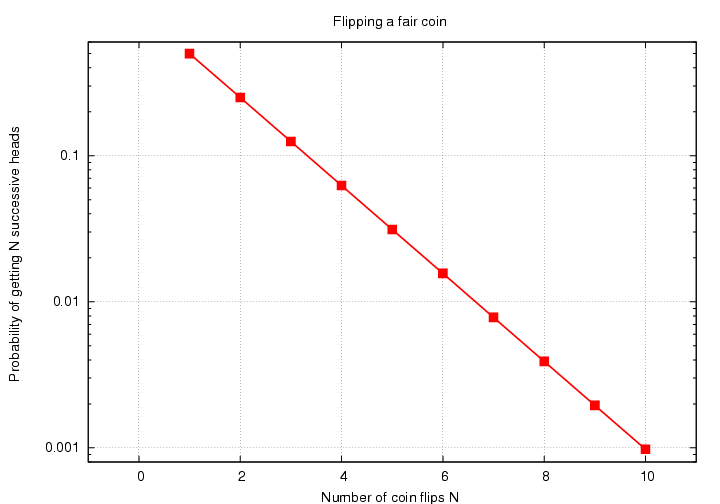
Okay, let's get back to baseball. Let's look at hitting streaks in the simulations. There are a LOT of simulated seasons: roughly 55,000, in fact (there are roughly 1000 players who come to bat during a typical season, due to minor leaguers who are added briefly to their parent team's roster). Even though long hitting streaks are uncommon, we'll have plenty of them in this large dataset. Let me count the number of streaks as a function of length.
Length N Number of streaks at
least N games long
----------------------------------------------
30 17,460
35 4,493
40 1,221
45 359
50 102
55 29
56 23
60 9
-----------------------------------------------
If we plot the number of streaks at least N games long against N, using a logarithmic vertical scale, we see the same sort of linear relationship.

The mathematical relationship in this case is a bit more complicated, but it still involves a base value raised to some power which involves N. One way to describe this particular relationship is
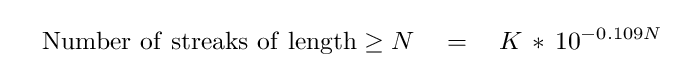
Here, we use 10 as the base of the exponential, rather than 0.5. The constant K which best fits the data has a value of about 31 million, but the important part of this relationship is the exponent: -0.109 * N. I've drawn a green dashed line in the diagram to show how well this mathematical relationship fits the simulated data.
We can use that exponent to make quantitative statements about the number of streaks. Each time we increase the length by a single game, from, say, N ≥ 45 to N ≥ 46 games, the number of streaks shrinks by a factor
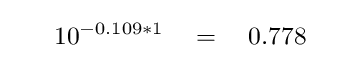
A brief digression: can we interpret this factor 0.778 in some way? Sure! Suppose a batter has 4 at-bats in a game, and has a batting average of 0.300. What are the chances that he fails to get a single hit? For each at-bat, the probability that he fails to hit safely is (1.0 - 0.300) = 0.700, so if he has 4 at-bats, the probability of 4 outs is (0.700)*(0.700)*(0.700)*(0.700) = 0.240. Now, the probability that he does NOT make 4 outs, and so has at least 1 hit, is (1.0 - 0.240) = 0.760. That's close enough to 0.778 to show us that the explanation is along these simple lines.
If we increase the length by 5 games, from, say, N ≥ 45 to N ≥ 50 games, the number of streaks shrinks by a factor

That looks almost too nice a fit to be true. Is it perhaps some consequence of our random number generator, or other factor in the simulations? Well, let's see what the distribution of REAL hitting streaks is.
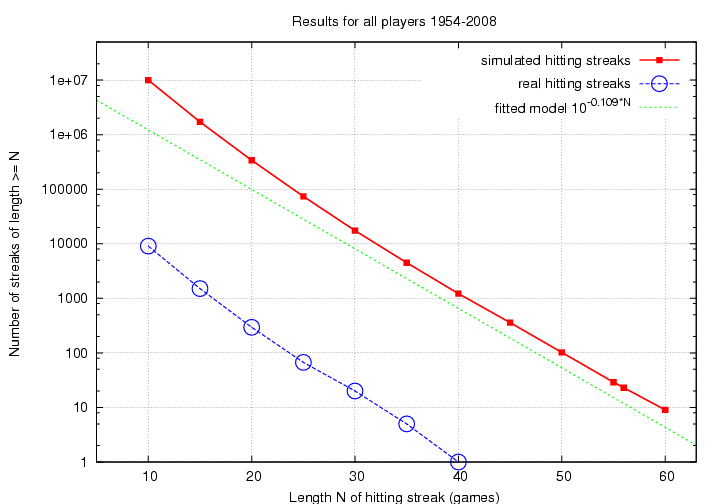
Both the real and simulated distributions show a small curve upwards at short lengths, N < 25 or so, but the look pretty similar overall. Let's normalize the simulations: since we ran 1000 simulations for each real season, we'll divide each number of simulated streaks by 1000.
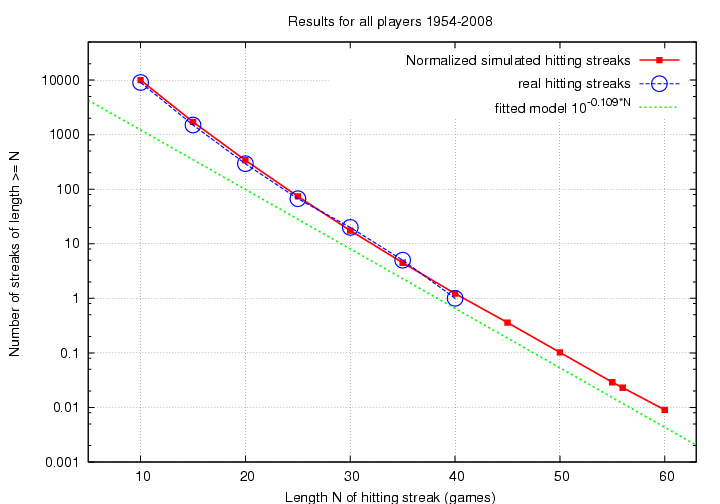
I would say that the simulations do a pretty good job of matching the distribution of actual hitting streaks. Both distributions curve away from the exponential model for short lengths; that's very likely due to large number of batters with few plate appearances (pitchers and minor-league callups) who generate many short streaks, but never any long ones.
I've been making the assumption throughout this entire document that it is possible to use a random-number generator to simulate the actions of real human beings; that is, I've been using random numbers and the the season-ending batting average for a player to predict whether he gets a hit or an out in every at-bat. Is that really a good assumption? Is there some way to test it?
One way to test this model for human behavior is to examine closely the distribution of hitting streaks, comparing the number of actual streaks of some length to the number of simulated streaks of some length. The results from the previous section indicate that the model isn't a really bad one; after all, the graphs show distributions with very similar slopes. But that's just an eyeball test -- can we make a more quantitative, statistical test?
I think the answer is "yes." Now, I'm not a statistician, so I may be making some mistakes in the discussion which follows, but I'll give it a try. Please feel free to contact me with comments and suggestions about my method.
Here are the two distributions, one real and one simulated, listing the number of consecutive-game hitting streaks of at least a certain length.
Hitting streaks over the period 1954-2008
length of real simulated simulated
at least (1000 instances) divided by 1000
-------------------------------------------------------------------
10 9057 10008872 10008.9
15 1508 1716957 1717.0
20 294 339869 339.9
25 67 73839 73.9
30 20 17460 17.5
35 5 4493 4.5
-------------------------------------------------------------------
I'll use a chi-squared test to compare the real distribution to the normalized simulated distributions, following the discussion given in my copy of Numerical Recipes in C. Suppose we pick one particular length for a streak; for example, streaks at least 15 games long. There are 1508 real streaks of this sort, and 1717 simulated ones. I can compute a chi-squared value for this length like so:
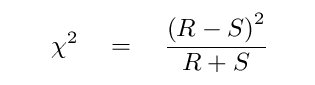
where R = 1508 and S = 1717. The result is a value of about 13.5. If this value is small, then the two distributions are similar at this length; if this value is large, then the two distributions are different at this length.
Now, suppose I compute chisq values for a range of streak lengths, and add them all up, like so:
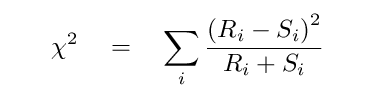
There are statistical arguments which predict the values this chisquared statistic OUGHT to have if the two distributions are really consistent with each other -- meaning they are both instances of the underlying population, or were both generated by the same kind of process. By comparing my computed value to these predicted values, I can make a claim that "the distribution of real streaks is consistent (or NOT consistent) with the distribution of simulated streaks, to some degree of confidence."
I'll choose a standard level of confidence: 95 percent. In other words, when I make my claim, I'll be saying, "there's only a 5 percent chance that the result I am stating could have arisen by random fluctuations," or, in more ordinary language, "it's very unlikely that the result I am stating is wrong due to chance." Please don't misunderstand: the results I state might still be wrong due to my poor choice of a model for comparison, or due to some systematic effect in the measurements or the simulations that I don't understand.
With all those disclaimers, let me give you a second version of that table, this time adding a few new columns.
Hitting streaks over the period 1954-2008
length of real simulated chisq for running total
at least divided by 1000 this length of all chisq
-------------------------------------------------------------------
10 9057 10008.9 47.5 47.5
15 1508 1717.0 13.5 61.1
20 294 339.9 3.3 64.3
25 67 73.9 0.3 64.7
30 20 17.5 0.2 64.9
35 5 4.5 0.03 64.93
-------------------------------------------------------------------
The fourth column here is the important one. If the value in this fourth column is much larger than 1, then the model is a poor fit to the observations. It appears that, for short streaks, the model -- in which batters always have the same chance of making a hit in each at-bat -- is not a very good fit to the data. The computer model produces a larger number of 10-game and 15-game hitting streaks than are seen in the actual game records. For longer streaks, on the other hand, it's pretty good.
I don't know if this seeming difference is even meaningful; there may be some aspect of the dataset that places some bias into the observations. If the difference is real, and there really is some aspect of hitting a baseball which makes it easier (or harder) than average on short time scales, one could imagine any number of explanations. I'll leave it to the reader to do so.
 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.