Making quantitative measurements using CCD images (II)

Michael Richmond
Jun 20, 2014

Contents

• Aperture photometry: a better way to measure stellar brightness
• Exercise: measure IY UMa

Aperture photometry: a better way to measure stellar brightness

As you may recall from the first lecture in this series , our goal was to measure the brightness of some stars in the field of the spiral galaxy M74. We can use this image of M74 taken at the RIT Observatory:

• Download the file r020_clean.fit (FITS format)

It should look something like this:

I've labelled a few objects for future reference.

Now, if you look at the image above, it should be obvious that the star "A" is much brighter than the object labelled "SN" (which is actually SN 2013ej). The question is: exactly how much brighter is it?

The last time around, we used a very simple method to answer this question: we simply measured the brightest pixel in each object, subtracted away the sky contribution from the value, and stopped. In other words, our algorithm was:

1. measure brightest pixel in an object = "peak"
2. measure typical sky value near the object = "sky"
3. compute final result:

   
            result  =   peak - sky
     

It's quick and easy ... but not very accurate.

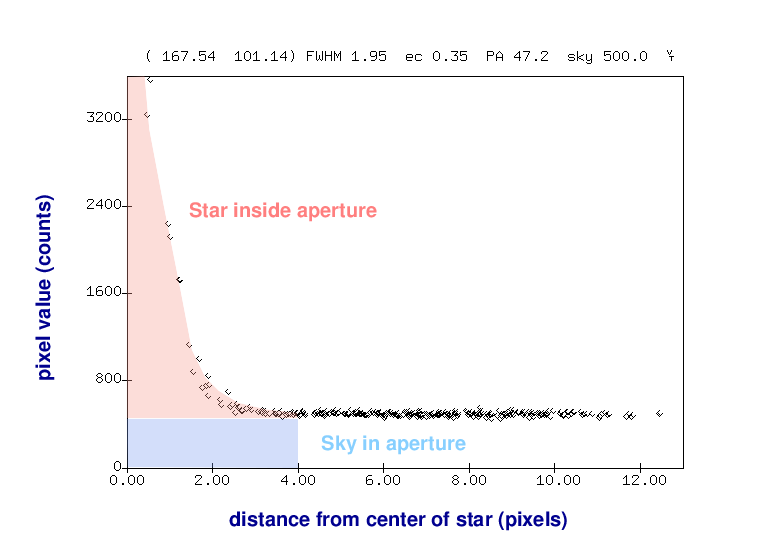
We can illustrate this method with a radial-profile graph of the star. On the horizontal axis is the distance of each pixel away from the center of the star, and on the vertical axis is the pixel value above the local sky value.

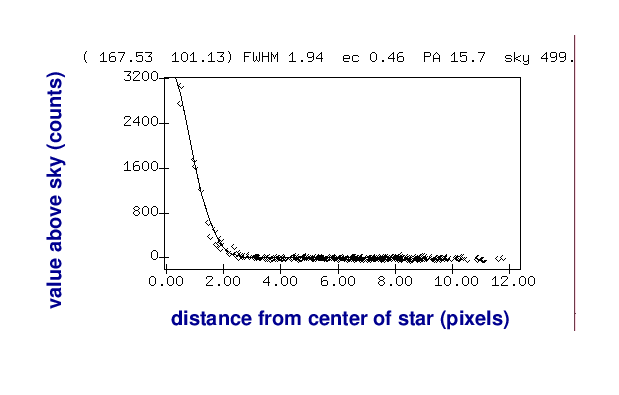
So, our simple method is just to pick the largest pixel value in this graph:

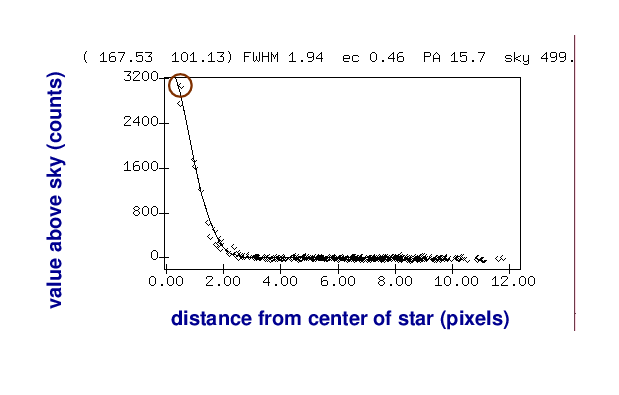
As you can imagine, this isn't very accurate for several reasons. Depending on the exact position of the star on the CCD, the peak of the point-spread-function (PSF) might fall at the center of the pixel, or near the edge, or even near the corner; the amount of light recorded by that pixel would vary in each case.

A better approach is to add up all the light which falls onto the CCD within a small region around the center of the star:

Of course, that will mean that we include some light from the sky as well.

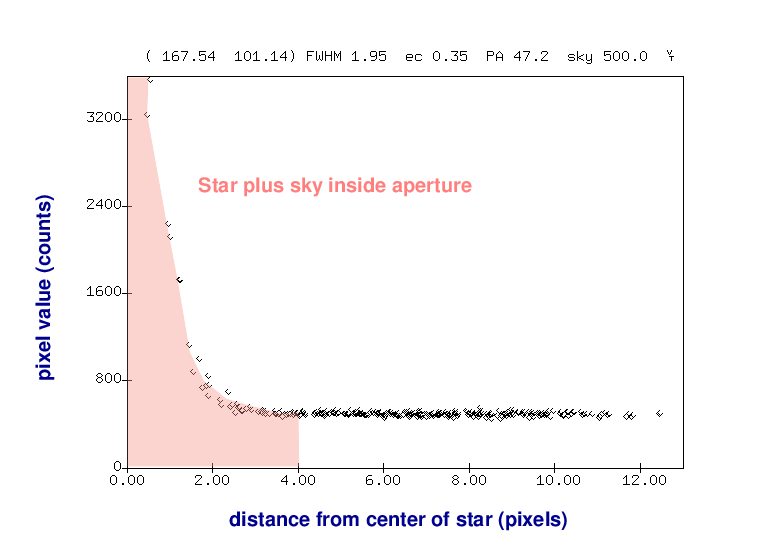
But we can then use an annulus around the star to measure the typical sky value, without any contamination from the star's light.

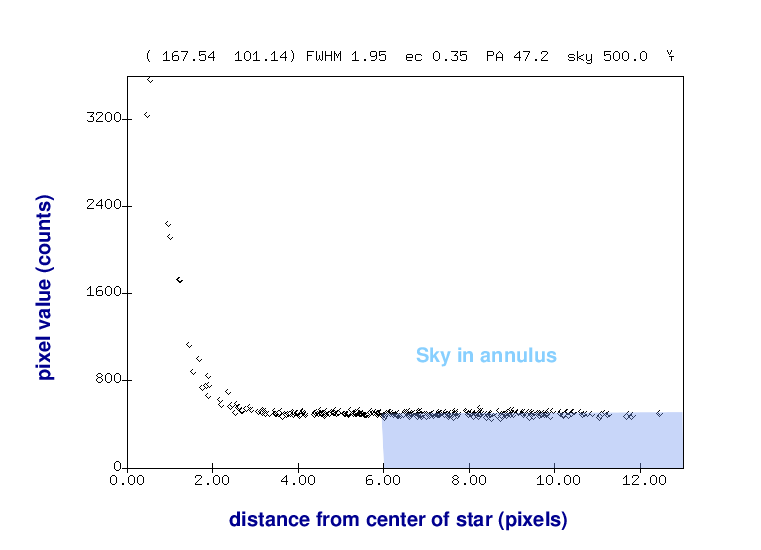
Once we know the local sky value, we can go back to our measurement of light inside the aperture and remove the contribution from the sky -- leaving a good measurement of the light from the star, all by itself.

Okay, let's try this method. Can you use your image of M74 to

1. add up the light from (star "A" plus sky) inside an aperture of radius R = 5 pixels. This circle will contain (pi * 5 * 5) = 78 pixels.
2. determine the typical sky value per pixel in a region near star "A"
3. compute the light from star "A" only, like so:

   
   
     counts_A   =   ("A" plus sky in aperture)  -  (sky/pixel nearby) * 78 pixels
   
     

Now repeat to measure the brightness of the SN.

4. add up the light from ("SN" plus sky) inside an aperture of radius R = 5 pixels.
5. determine the typical sky value per pixel in a region near "SN"
6. compute the light from "SN" only, like so:

   
   
     counts_SN   =   ("SN" plus sky in aperture)  -  (sky/pixel nearby) * 78 pixels
   
     

And now you are ready to compute the difference in brightness between the SN and star "A", in magnitudes.

             (mag SN) - (mag A)  =    

Exercise: measure IY UMa

Let's practice by making measurements of three objects in the field of the variable star IY UMa , which is at RA = 10:43:56.73, Dec = +58:07:31.9 (J2000).

You can download FITS images of this field from one of my courses, if necessary:

• Directory containing FITS images of IY UMa

Use aperture photometry to measure the instrumental magnitudes of the stars "A", "B", and "IY". Choose an aperture of radius 5 pixels, and make sure to subtract the local background sky value if you can; if you can't, then subtract a global sky value from all measurements.

We'll break up the big list of images into small sets of 5 or 10 per person, so that this doesn't take too long.

When you have finished, make a table that looks something like this:

image        A       B         IY
1          12.592   13.670   13.079  
2          12.612   13.642   13.091 

When everyone has finished, I'll make a light curve of these stars by graphing the instrumental magnitudes (on the vertical axis) against the image numbers (on the horizontal axis).

For more information

• The first talk in this series was Making quantitative measurements using CCD images (I) (May 29, 2014)
• You can find the FITS images of IY UMa used for the exercise described in this document by visiting

  http://spiff.rit.edu/classes/phys445/work/apr11_2006/

  You should find 99 images, each a simple 16-bit integer FITS image, 510-by-340 pixels in size.

Copyright © Michael Richmond. This work is licensed under a Creative Commons License.