 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Contents
If you want to make quantitative measurements of an object's brightness which can be compared to those in the standard astronomical catalogs or literature, you must use one of the standard astronomical filters. Unfiltered images will yield only very rough values for the brightness of a star or galaxy.
What are the standard astronomical filters? Well, one thing that they are NOT are the good old photographic RGB filters. You may see some companies selling filters which can be used to make composite color pictures, like this:

Unfortunately, while these filters aren't wildly different from some of the standard astronomical filters, they aren't exactly the same, either. Take a look for yourself:
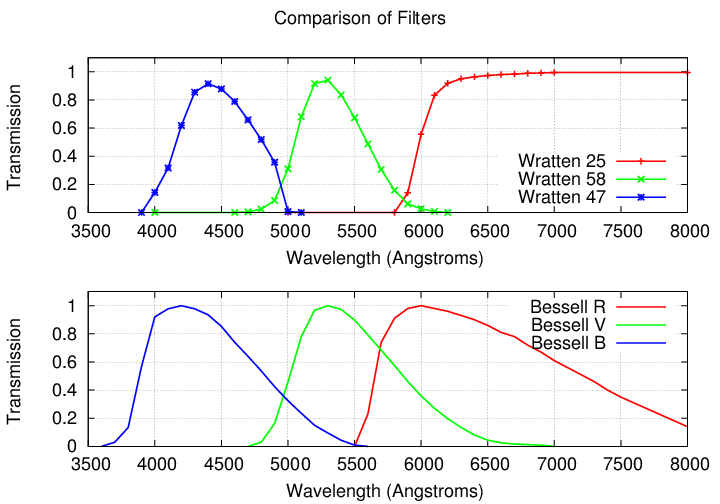
So what are the standard astronomical filters? There are several different sets, but the most common are
The first set listed, known as the "Johnson-Cousins" or "Johnson" set, is probably the most common. You might also see it called the "Bessell" set, since Bessell wrote a paper describing a simple way to make them. If you look around at catalogs of astronomical goods, you can find sets of these filters ....
Now, even if you do purchase one of the proper filter sets, it's very likely that your particular combination of
will end up yielding slightly different overall bandpasses than the standard ones. Depending on the type of scientific project you are doing, you might need to perform color transformations to convert your measurements onto the standard magnitude system. That's a rather complicated topic all by itself, though, so I'll leave it for a future discussion. If you just can't help yourself, you might peek at a brief description of the problem, and how to address it.
Okay, so you get the proper filters, attach them to your telescope, focus the camera, and get everything working. It's time to pick a target. How about --- the spiral galaxy M74?
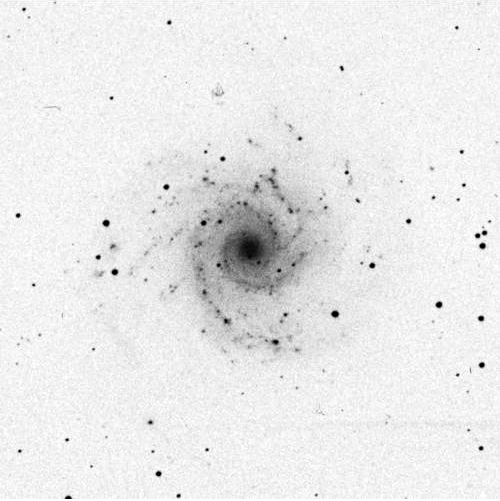
Let's take a 30-second long exposure through the R filter. Ready .... go!
tick tick tick .... ping!
Great! I happen to have a copy of this image in FITS format. Please download the FITS image, if you can, and display it on your computer.
You should see something like the picture below -- if you don't, try modifying the contrast levels in your display program.
Yuck!
That looks terrible. What's wrong?
When you acquire an image at the telescope, the image does (we hope) contain information about your target object, based on the photons from that target which were focused onto the camera by your telescope. But the image also reflects the influence of several other factors, and, as a result, can't be used yet to make good measurements. We call this a raw image.
In order to "clean" the image, we need to remove those other influences, as well as we can. Two of the most common types of contaminating factors are called by astronomers
Let's look at "dark current" first. When a photon strikes a CCD, it knocks one electron out of a silicon atom; the electron can then be pushed and pulled across the chip by electric fields to lead it to a device which counts it. One photon produces one electron.
BUT -- there is another way for electrons to be knocked free inside the silicon of the CCD. Each atom is vibrating slightly within the crystal structure; the higher the temperature, the more violent the vibration. If one atom bangs into its neighbor hard enough, it may eject an electron, which then is swept up by the electric fields and counted together with all the photon-based electrons. The result: extra electrons, NOT produced by light. Astronomers call this "dark current."
What's worse, these thermally produced electrons aren't uniform across most CCD chips. If there are impurities in the chip -- places where an arsenic atom, for example, has sneaked into the crystal, or where the crystal structure has a slight break -- electrons may be liberated more easily. This can cause some pixels to produce much more dark current than average: "hot pixels."

How can we get rid of these extra electrons? The basic idea is to take a dark image, which is just an image with the same exposure time as the target image, but with the shutter kept closed. Since no light strikes the CCD, the only electrons which are counted will be those knocked free by thermal motions. If the behavior of the chip is nice and stable, and if the dark frame was taken at the same temperature as the target frame, then the number of "dark" electrons in each pixel ought to be roughly the same in both images.
One can create a better "dark frame" by taking a series of 5 or 10 or 20 individual dark images, then combining them via an average or median technique.
I just happen to have a 30-second long dark image (actually, the median of ten such images) right here. Take a look:
After creating a "dark frame", one simply subtracts it from the raw target image.
(dark_subtracted image) = (raw image) - (dark image)
Can you subtract the dark image from the raw picture of M74?
Here's what it looks like when I do it:
So, that's better ... but we're not done yet.
The next step is to remove the effect of imperfections in the optical path of the telescope and camera. If there are any dust particles on the filters or the camera's window, or if light from the sky bounces off the inner surface of the telescope tube, or if the optics don't fully illuminate the camera, or any of a host of other problems, then the pictures we take will have regions which are a bit brighter -- or darker -- than they ought to be. Astronomers call these flatfield variations.
For example, if I take a picture of a blank sheet of white cardboard hanging from the inside of my telescope's dome, I should see a blank, featureless, uniform picture. But what I actually see is this:
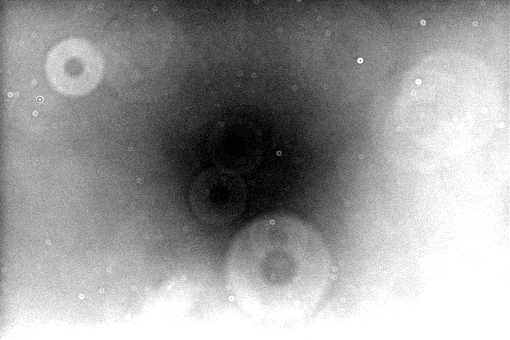
You can see very faint hints of these same patterns on the dark-subtracted image, if you boost the contrast to very high levels:

To remove these flatfield defects, we need first to create a good "flatfield image" by taking pictures of a blank card, or a portion of the blank sky at twilight.
Next, we normalize the flatfield image, which means divide every pixel by the overall mean value of the image. That will leave us with an image with mean value 1.0, but some regions will be a bit brighter (1.02, 1.01) and other regions a bit dimmer (0.99, 0.97). If we then divide our dark-subtracted target image by this normalized flatfield image, we'll boost the image where it was artificially dark, and pull it down where it was artifically bright.
Q: What is the mean value of the flatfield image?
(clean image) = (dark_subtracted image) / (normalized flatfield image)
Can you normalize the flatfield image, and then divide the dark-subtracted image by the normalize flat?
Here's what it looks like when I do it:
Okay, we finally have a clean image of M74:
We are now ready to measure the brightness of stars in this image. Let's focus on just two of them, which I'll label "B" and "X".

It seems obvious that "B" is brighter than "X" -- but by how much? Is it 0.50 mag brighter? 1.00 mag brighter? 1.50 mag brighter? How can we measure stellar brightness?
Q: How can we measure stellar brightness?
Well, one easy -- but very imprecise -- method is just to pick out the value of the peak pixel in each star.
peak pixel
---------------------------------------------------------
star B
star X
---------------------------------------------------------
But wait! We've forgotten something: the light from each star isn't the only light in this image: there's also background sky light. Every pixel in the clean image contains light from the general sky; here in Rochester, most of that is due to light from nearby parking lots and buildings. We need to subtract that "sky" light from each pixel value before we compare the two stars.
Q: What is the general background sky value in this image?
peak pixel sky (peak - sky)
---------------------------------------------------------
star B 3571 - 498 = 3073
star X 1043 - 498 = 545
---------------------------------------------------------
Okay! So, we can see that star "B" is brighter than star "X" by a factor of roughly 6.
Q: How can we compute the difference in magnitudes
from this ratio of intensities?
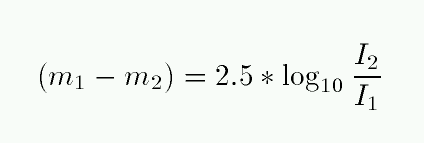
Q: Okay, so what is the difference in magnitude?
(mag B) - (mag X) =
Now, remember that this method -- using the peak pixel value -- is a very poor way to measure stellar brightness. We'll investigate better methods in a future discussion. But let's just take one last step for now.
At this point, you have determined that, not only is star B brighter than star X, but it is about 1.88 magnitudes brighter in the R passband. Okay, that's all well and good ... but it would be much more satisfying to be able to write something like
"star X has an R-band magnitude of ________ "
In order to do this, we need to calibrate our measurements; or, in other words, we need to put them onto the standard Johnson-Cousins R-band magnitude system. How can we do THAT?
Let's do this the easy way.
File -> Load catalog -> Surveys in Vizier -> UCAC4
Q: What is the r-band magnitude of star "B" ?
Q: What is the r-band magnitude of star "X" ?
 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.