 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Today, I'll talk very briefly about the progress we have made in measuring the size of the cosmos. It's impossible to mention even briefly all the important events, so I'll restrict the discussion to just four particular experiments. We'll begin with the ancient Greek astronomers as they determine the size of the Earth, and then the distance between the Earth and the Moon; then we'll jump forward in time to the Renaissance and watch as astronomers move beyond our own planet to estimate the scale of the entire solar system. My goal is to give you some notion of HOW we can measure these vast distances, and an appreciation for the difficulties our scientific ancestors had to overcome.
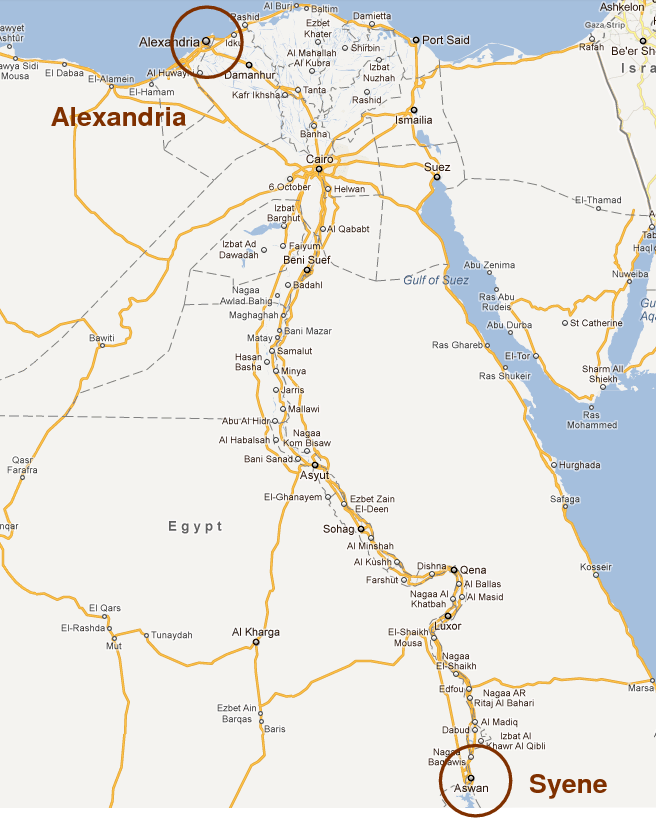
The first step to measuring the solar system is to determine the size of one of its constituents: the Earth. The first really good estimate is attributed to the Greek scientist Eratosthenes of Cyrene, who lived in the third century BC.

Eratosthenes heard that in the Egyptian city of Syene (the modern Aswan), the sun passed directly overhead on the summer solstice -- so that a person could see a reflection of the Sun by looking down into a well, and a stick would cast no shadow, But he also knew that in Alexandria, on that same day, the Sun did NOT pass overhead. Instead, in Alexandria, sticks cast a short shadow which one could measure.
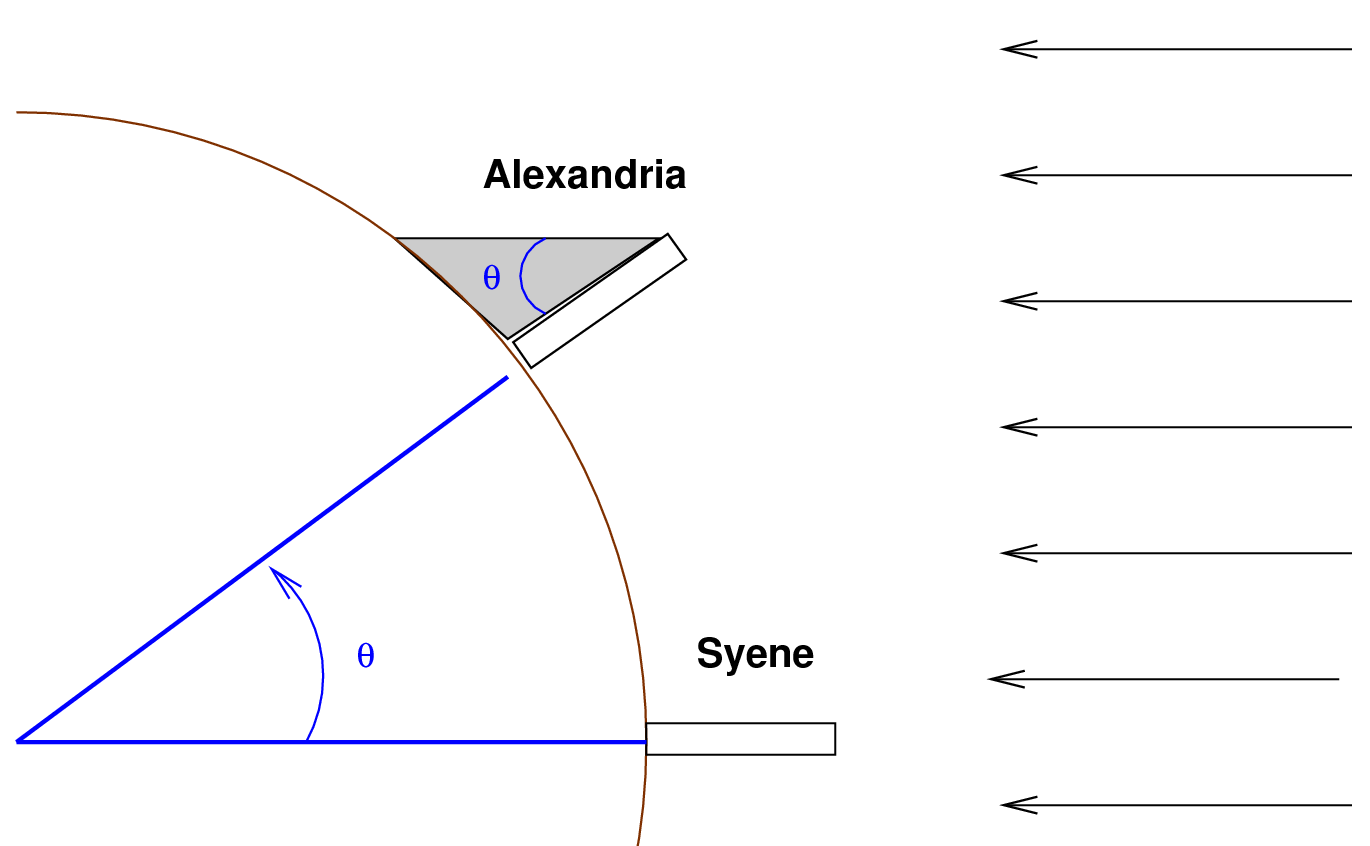
Eratosthenes used the length of the shadow cast by a stick in Alexandria to figure out that the angle θ between the stick and the shadow was about 7.2 degrees, or about 1/50 of a full circle. He assumed that Alexandria was due north of Syene (which isn't quite true), and that the distance between them was 5000 stades, based on traveller's reports. Calculating the circumference of the Earth was then easy:
distance around the Earth = 5000 stades * 50
= 250,000 stades
This is the value given by Cleomedes; other sources provide a circumference of 252,000 stades.
It's not exactly clear how many meters correspond to the ancient unit of length called the stadion, but it's probably around 157 meters; using this value, one can say that Eratosthenes deterimed that the circumference of the Earth was about 39,250 km. And that means
|
Roughly one century after Aristarchus, the Greek astronomer Hipparchus made the first really good measurement of the distance to the Moon. Hipparchus was a careful observer as well as a good mathematician: he created one of the best surviving catalogs of stars from ancient times and used it to discover the precession of the equinoxes.
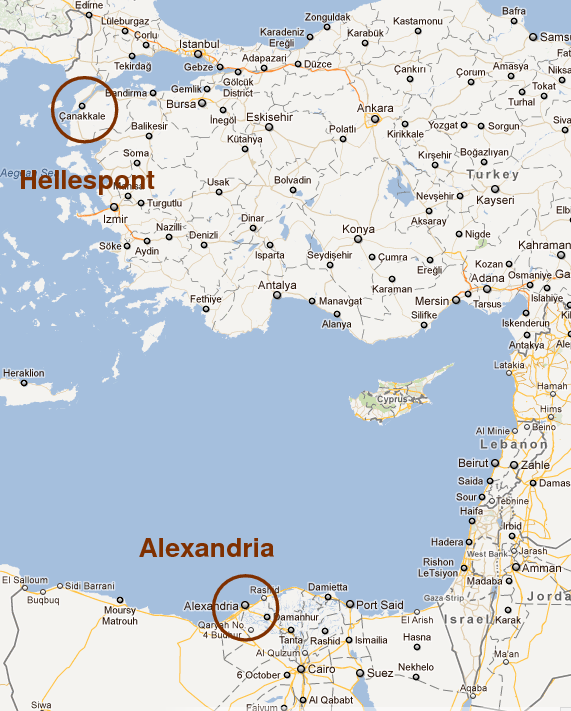
Hipparchus studied a solar eclipse -- I'll assume it was one which took place in 129 BC, although it might have been one which was observed in 190 BC. People near the Hellespont saw a total solar eclipse, while those in Alexandria observed a partial eclipse.
Hipparchus realized that, although the Moon was blocking the entire disk of the Sun, as seen from the Hellespont ...
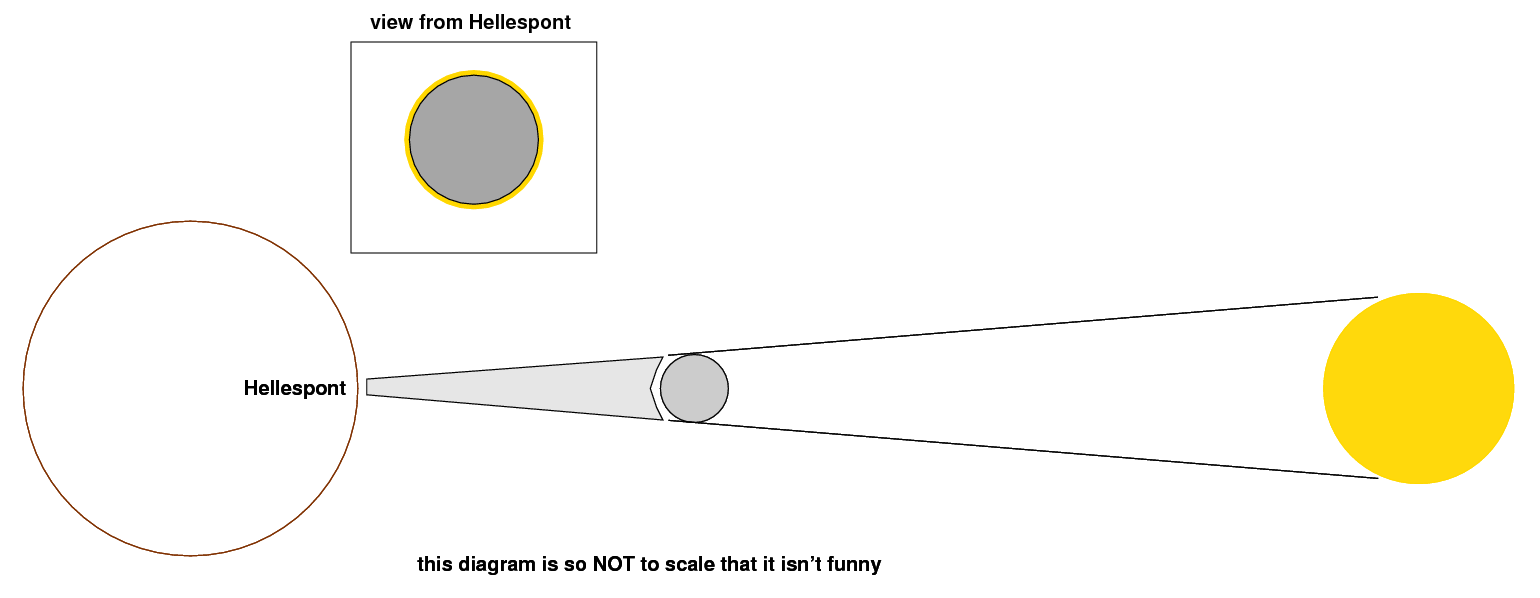
... the Moon was only blocking a portion of the Sun, as seen from Alexandria.
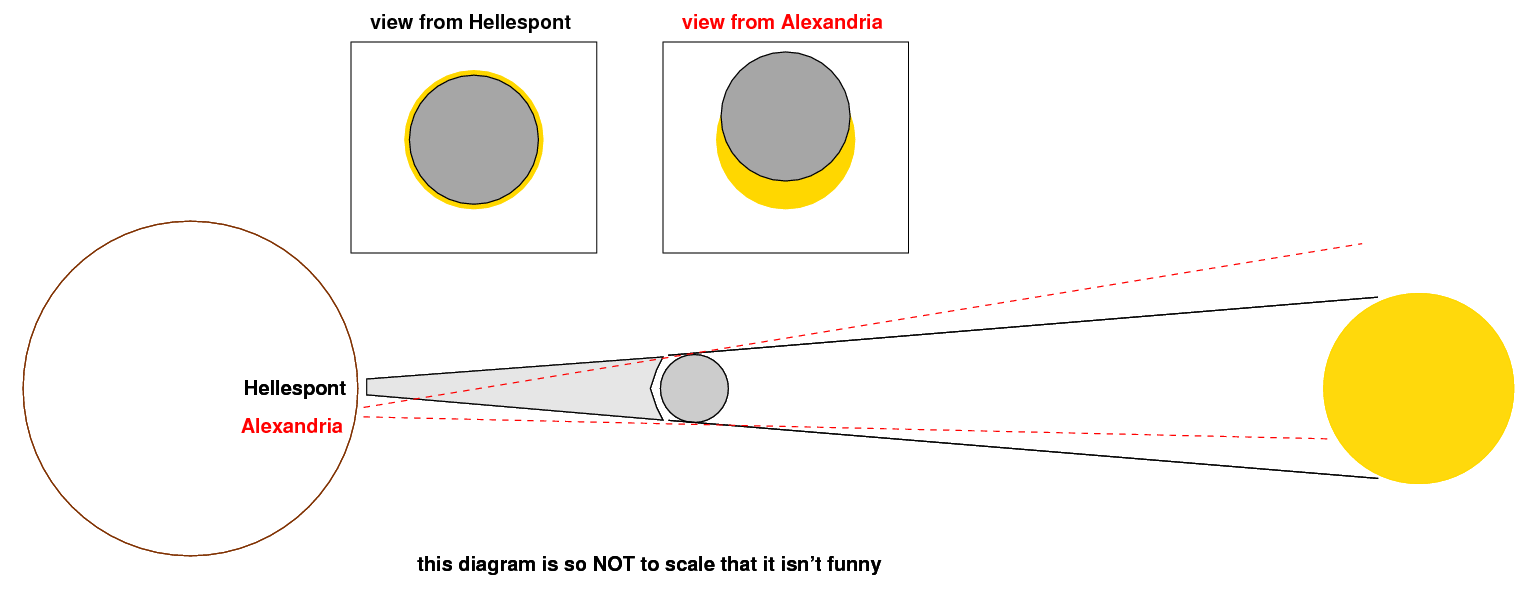
In fact, the reports from Alexandria indicated that the Moon was displaced by 1/5 of the Sun's diameter. Since the Sun's angular diameter is about half a degree, this meant that the Moon was displaced by about (1/5) * (1/2) = (1/10) of a degree when seen from Alexandria, relative to when seen from the Hellespont.
Hipparchus realized that he could use this information to draw a very skinny right triangle:
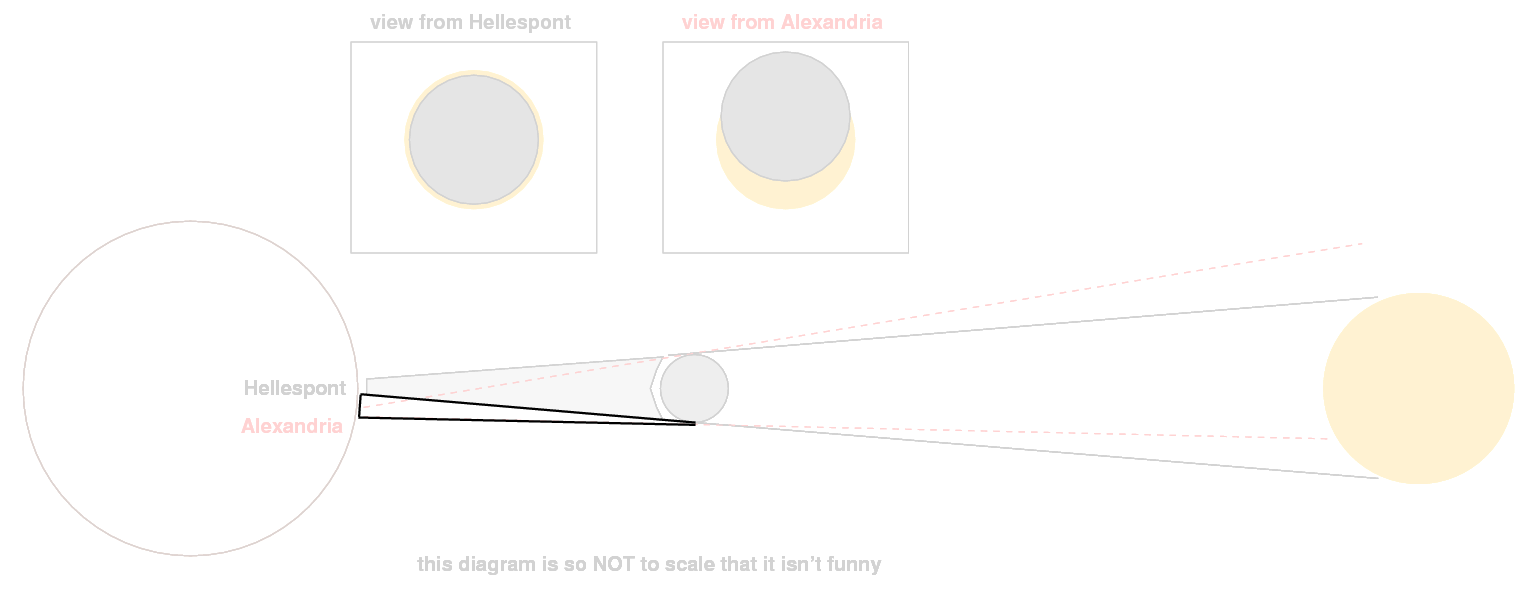
If we zoom in on that triangle, we see that it touches the Earth at two locations, separated by a distance L.
Yes, yes, this isn't really a right triangle. Yes, the two locations are not located exactly along a north-south line. Yes, the sun and moon weren't directly overhead. This is a simplified version.

Since the Hellespont and Alexandria are nearly along a north-south line, the distance L between them can be calculated if one knows the radius of the Earth and the difference in their latitudes. Hipparchus knew that difference in latitudes -- about 9 degrees -- and he had a pretty good value for the radius R of the Earth from Erothosthenes.
9
L = ( --- ) 2 π R
360
And with this value for L, Hipparchus could use a little trigonometry to calculate the distance d to the Moon:
L
d = ( ------- )
sin θ
Using a measured θ = 0.1 degree, based on the appearance of the eclipse, Hipparchus computed a distance to the Moon of
d =~ 90 Earth radii (vs. about actual value of 60 Earth radii)
That's not bad! Remember, we made a number of approximations in this little analysis. As a more careful analysis of this method shows, it can yield a better result, about 67 Earth radii.
Hipparchus wasn't done, though. In addition to the method above, based on a solar eclipse, he used measurements of the Moon and the Earth's shadow during lunar eclipses to make an independent measurement of the distance to the Moon. In that case, his results fell into the range from 62 to 72 Earth radii. So, to summarize,
|
So, Greek astronomers were able to determine to a fair degree of accuracy the size of the Earth, and the distance between the Earth and Moon. However, at this point, they were stuck. When they tried to measure the distance between the Earth and Sun, for example, they were so wrong that it didn't really help. Aristarchus, for example, estimated that the Sun was about 20 times more distant than the Moon ... but the true ratio of distances is close to 390.
Why couldn't the Greek astronomers do a better job? One reason was their lack of good instruments. The Moon is close enough that observers in different locations on Earth will see differences in its position (parallax) which are around 0.1 - 0.3 degrees in size, big enough that the naked eye can detect them. The Sun (and other planets) are so much more distant that their parallaxes are tiny: the Sun, for example, has a parallax of about 0.002 degrees.
Try detecting some tiny shifts for yourself.
Q: Can you detect an angular shift of 0.2 degrees? Q: Can you detect an angular shift of 0.002 degrees?
For the next fifteen hundred years or so, the (correct) knowledge of distances out into space was stuck at the Moon. Venus, Mars, Jupiter, the Sun -- we just didn't have a clue.
The person responsible for breaking us out of this very local volume and extending our reach to much larger distances was, well, two people, really.
The first was Tycho Brahe, a Danish nobleman who took up astronomy in a big way.

This image of Tycho courtesy of
the History Blog
The telescope had not yet been invented, back in the late 1500s, but Tycho didn't let that stop him. He built a set of instruments which allowed him and his assistants to make very accurate measurements of stellar positions. In addition, he took meticulous notes of the data. The precision of his measurements reached about 1 arcminute, or 1/60 of a degree = 0.016 degree , enabling astronomers to address many questions which were previously impossible to answer.

Image from Tycho's
Astronomiae instauratae mechanica
courtesy of the
Treasures of the Bodleian Library
Tycho hired German mathematician Johannes Kepler to be his assistant and scientific heir.

After Tycho died soon thereafter in 1601, Kepler began to explore the rich treasure of measurements in Tycho's notebooks. He spent decades using the data to support a number of discoveries. One of them was a relationship between the period and size of a planet's orbit -- which we now call Kepler's Third Law, but which he considered to be a reflection of celestial harmony. As he puts it in his book Harmonia Mundi (1619)
For after finding the true intervals of the spheres by the observations of Tycho Brahe and continuous labor and much time, at last, at last the right ratio of the periodic times to the spheres ... the ratio which exists between the periodic times of any two planets is precisely the ratio of the 3/2th power of the mean distances.
Kepler, Harmonia Mundi Book Five, translated by Charles Glenn Wallis.
Or, in a more compact form,
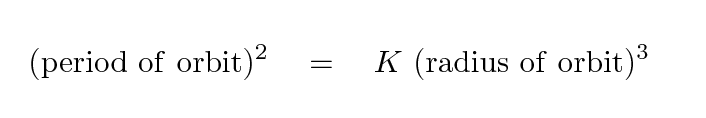
Now, the PERIOD of a planet's orbit is not so difficult to measure: if you watch the skies carefully, week after week, year after year, you'll see the planets move from one constellation to another, making a circuit around the section of the sky we call the zodiac. There's one small complication, due to the fact that we are observing the planets from a moving platform (the Earth), but one can account for that. Since astronomers had been keeping records of planetary motions for thousands -- yes, thousands! -- of years, Kepler had very accurate values for each period.
Period (days)
Planet Kepler modern
---------------------------------------------
Mercury 87 87.97
Venus 224 224.7
Earth 365 365.26
Mars 686 687
Jupiter 4,332 4,333
Saturn 10,759 10,759
---------------------------------------------
Does this mean that Kepler could use his harmonic relationship to calculate the size of each planet's orbit? NO! -- except, in a way, maybe yes.
The problem was the term K in his equation above. He didn't know the value of that constant, so he could not convert a period (in days) into a radius (in meters). However, what he could do was to compare the orbits of two planets. For example, Mars and the Earth:

Q: Which is larger: the orbit of Mars or of Earth? Q: By what factor is it larger?
Yes, Kepler -- and all the scientists after him -- could figure out that the radius of Mars' orbit is about 1.52 times larger than the radius of the Earth's orbit. In other words, he could make a map of the solar system which showed the planetary orbits in their proper proportions
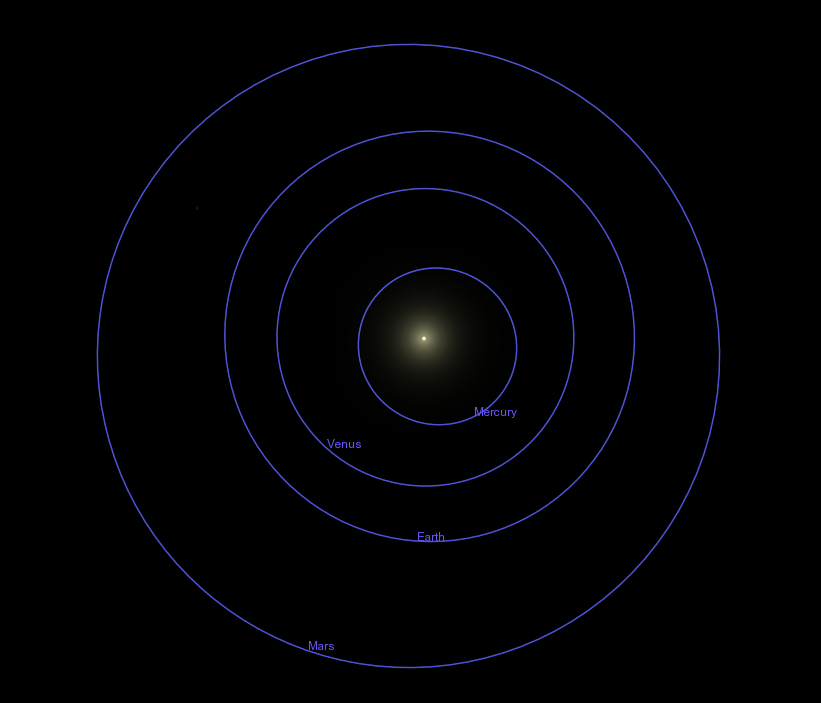
and he could even label those orbits in a quantitative manner, using the Earth's orbit as a standard.
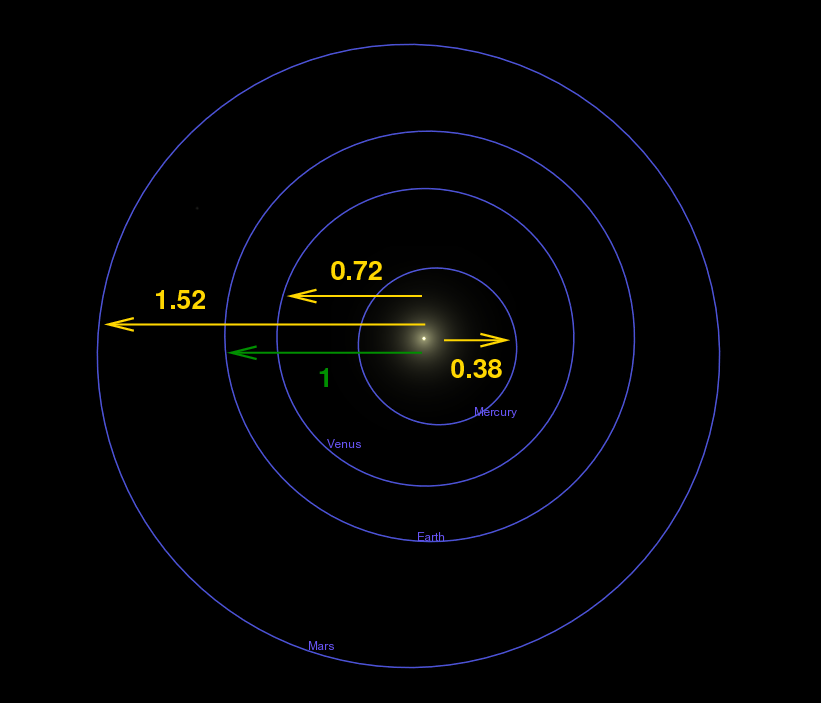
But the one thing he could NOT do was to compute the size of any planet's orbit in miles, or kilometers, or feet, or yards. Kepler was like a man who has a map without a scale.
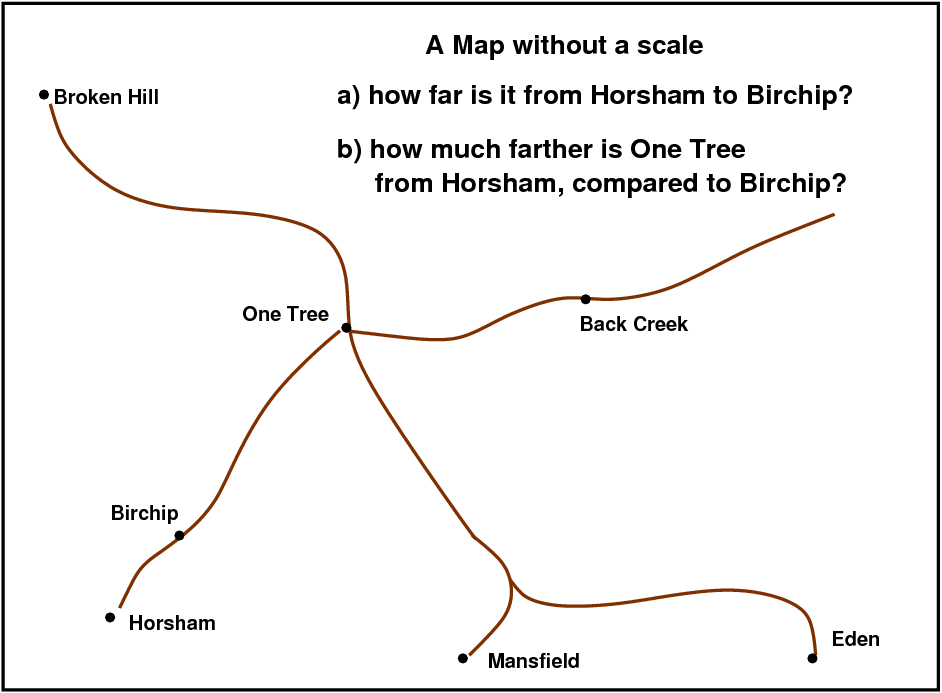
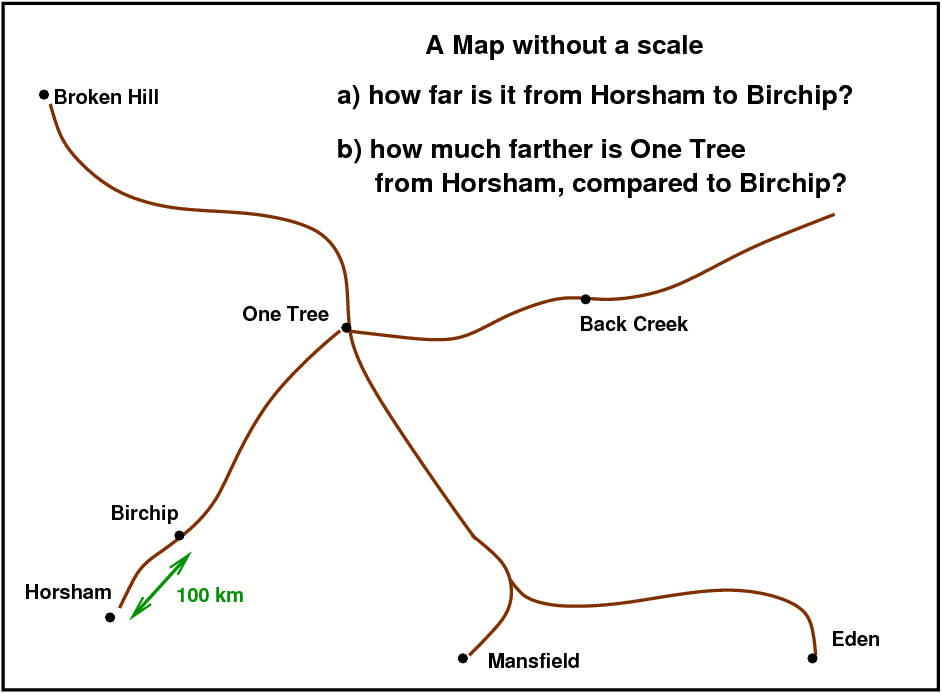
The owner of this map can answer question b), since the map shows that One Tree is about four times farther from Horsham than Birchip is; but he can't answer question a) -- the distance between Horsham and Birchip could be 5 km, or 15 km, or 50 km. There's just no way to know (unless you get a little help.)
What the owner of this map needs, and what Kepler needed, was just one distance. If we can measure the distance between just one pair of towns -- say, from Horsham to Birchip -- then we can figure out any distance on the entire map.
So ... thanks to Kepler's work, astronomers could ALMOST determine the size of the solar system. All they needed to know was the distance in kilometers (or miles) between any single pair of objects:
Astronomers figured out that the Venus-Earth distance would be the best choice. After all, no planet comes closer to the Earth than Venus, and the closer an object is to Earth, the easier it is to measure its distance.
However, there's a problem if we try to observe Venus when it is at the point in its orbit closest to the Earth.
Q: What's so difficult about observing Venus when
it is close to the Earth?
Two problems, actually:
Consider the situation about one month from now, on May 18, 2012.

Both Venus and the Sun are "to the right" of the Earth in space, so if we look towards Venus, we must also be looking nearly at the Sun. If you go out in the evening of May 18, 2012, a little after 9 PM, you will be able to see Venus, but only very low in the western sky; it will be about 13 degrees above the horizon as the sky begins to grow dark.

If you point your telescope at Venus, you'll be looking through a LOT of air, with all the dust and reddening and turbulence that implies. And even if you do manage to get a sharp image, what you will see is a long, thin crescent.

In order to compute the distance to Venus, astronomers at different locations on Earth need to make a PRECISE measurement of the position of the planet ... but how can you define the "position" of such a long, skinny object?
If only there were some way for us to observe Venus when it was obvious to astronomers all over the Earth how to define its position exactly ....
Q: Is there some occasion when Venus will
be close to the Earth, and, at the same time,
show some obvious feature with which
we can measure its position?
Yes!

|

|
| Image courtesy of John Walker | See the video of the 2004 transit by Antonio Cerezo, Pablo Alexandre, Jesús Merchán, David Marsán or a local copy |
The basic idea is again, just as it was for the Greeks, to use trigonometry. If observers at different locations on Earth view the same transit, they will see Venus cross the Sun along slightly different paths.
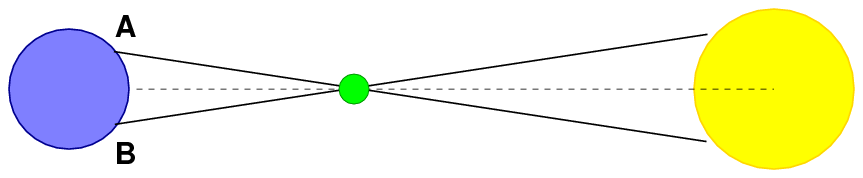
The scale in this diagram has been ruthlessly slaughtered in the
interests of clarity.
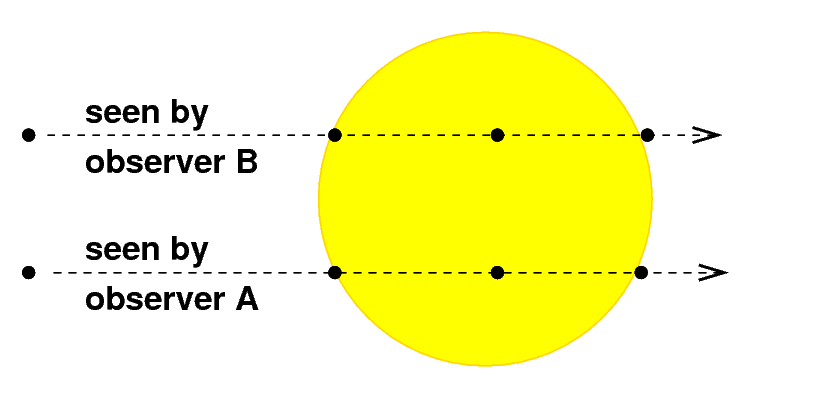
Ditto.
Now, in practice, there are a number of difficulties. For example, the ACTUAL shift in position of Venus as seen from two different places is a bit smaller than I've indicated so far. For example, observers in Nikolsk, Russia (latitude +53 North) and Antananarivo, Madagascar (latitude -18 South), would have seen the transit of 2004 as follows.

Click to activate. Thanks to
Stellarium!
The parallax angle for two observers far apart on the Earth is only 20 to 30 arcseconds, somewhat less than the apparent diameter of Venus itself. Moreover, each observer needs to have an accurate measurement for the time associated with each of his measurements. Several hundred years ago, that was a big deal, especially for astronomers who travelled to the far ends of the Earth on voyages which could take months or years.
"Travel to the far ends of the Earth?" I hear you say. "Why did they do that? Why not just sit at home and watch the transits in comfort?"
Oh, yes, I forgot to mention one thing about the transits of Venus. The orbit of Venus around the Sun is not quite in the same plane as the orbit of the Earth. Let me show you what I mean: click on the picture below to watch a short movie.

The consequence of this orbital tilt is that, most of the time, when Venus passes the Earth in its orbit, it is far above or below the Sun from our point of view. Click on the picture below to watch a short movie.
Venus passes DIRECTLY between the Earth and Sun only very rarely: only twice every 123 years. If you want to make the best measurements possible of this very rare event, you need to go to the spots on Earth where the Sun (and Venus) will be above the horizon during the entire eight hour duration of the transit. Moreover, in order to determine the distance to Venus, one must compare the measurements made by observers at locations spread all over the appropriate hemisphere, thousands of miles away from each other.
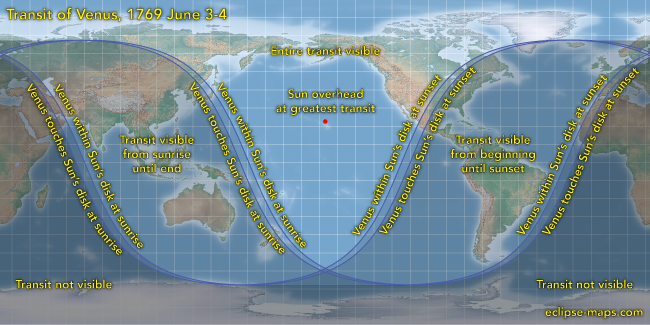
Consider, for example, the year 1769. Below is a map showing the visibility of the transit of Venus from different locations on Earth.
Q: Where was the best place to observe
the transit in 1769?
And so, the leading scientific powers of the day -- England and France -- sent expeditions into the Pacific. The leader of the English expedition was a fellow named James Cook.

Image courtesy of the
National Maritime Museum
Cook left England in August, 1768, and sailed across the Atlantic, around the tip of South America, and into the South Pacific Ocean. He reached Tahiti in April, 1769, several months before the transit would occur on June 3.

Map courtesy of
The Georgian Junkie blog
The weather gods smiled on Cook that day, so that he and his colleagues were able to observe the event without a problem. Some (but not all -- poor Le Gentil!) of the other expeditions also had success. Several years later, when all the measurements were combined and reduced, the results revealed for the first time an accurate distance between the Earth and Venus --- and that, in turn, told scientists the distance between the Earth and the Sun: the Astronomical Unit.
A number of scientists analyzed the results of these 1769 transit expeditions. If we look at the results published by seven different individuals within five years of the event, we find
|
After the transits of 1761 and 1769, astronomers had to wait until the late 1800s for another chance. In 1874 and 1882, a number of countries -- this time including the United States -- sent astronomers far and wide to observe the event. Well, SOME of them had to travel far and wide, but others were more fortunate. For example, one astronomer was lucky enough to live in just the right place:

Image courtesy of
the Albert R. Stone Negative Collection
Lewis Swift stayed at home, here in Rochester, and prepared to study the transit of 1882 with the 16-inch refractor of the Warner Observatory:

Image courtesy of
the Rochester Public Library Local History Division
Alas, it was cloudy. Are you surprised?
What were the results of the analysis of the transits of 1872 and 1884? The Astronomical Unit -- the basic scale bar for the solar system -- was now measured more accurately. An average of 10 different papers written before 1890 yields
|
One reason for the improvement was a big advance in technology: photography. Astronomers could now take pictures during the transit, and then, at their leisure, slowly and carefully measure the position of Venus on the images. Below is an example of a photograph taken at Lick Observatory in 1882.

Image courtesy of
a lecture by Paul Doherty
In August, 1898, Gustav Witt at the Berlin Observatory discovered an asteroid. Originally designated 1898 DQ, it was eventually given the name Eros after the young god of love. Within several months, astronomers around the world gathered enough information to allow an orbit to be computed. This asteroid, it turned out, would pass much closer to the Earth than the average asteroid.
Simon Newcomb, director of the Nautical Almanac Office at the US Naval Observatory, realized that this close approach would give astronomers an opportunity to determine the distance between Earth and Eros very precisely -- and, thanks to Kepler's Third Law, that could be used to compute a precise value for the Astronomical Unit.

Taken from
Newcomb, AJ 19, 147 (1898)
Newcomb mentions in this article the opposition of Eros in January, 1931. Why was that so special? The orbit of Eros is not nearly as circular as the orbit of the Earth: its eccentricity is 0.223, so there are times when it is much closer to the Sun -- and the orbit of the Earth -- than others. In 1931, Newcomb realized, the Earth would zoom past Eros at the same time that Eros was at the innermost position of its orbit.
So, in 1931, Eros would come within 26 million km of the Earth, closer than Venus ever comes (42 million km).
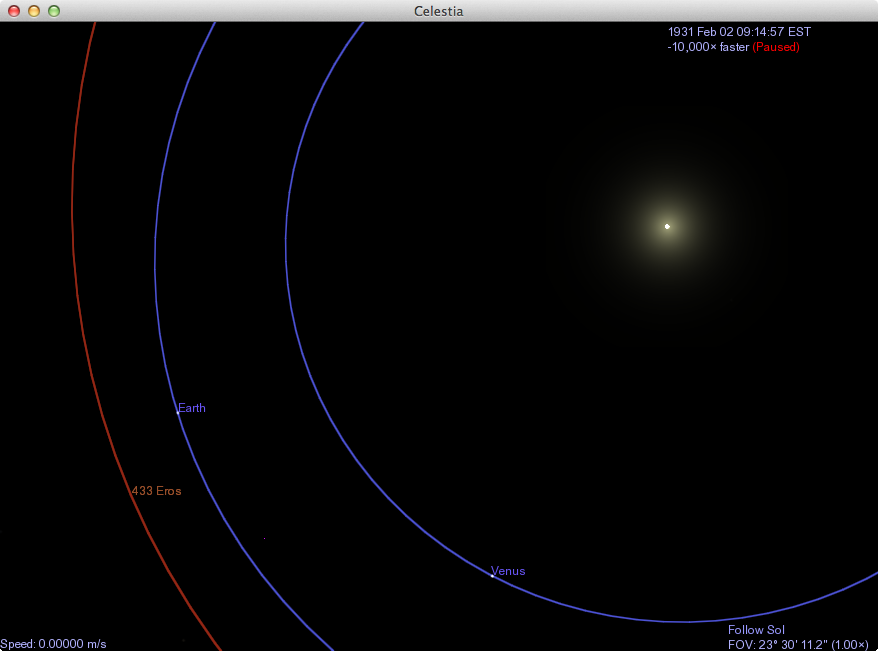
But that's only half of the reason that astronomers concentrated on Eros. The other half is the nature of observations of Eros, compared to those of Venus during a transit.
|
When astronomers tried to record the exact moment when Venus crossed the limb of the Sun, they discovered to their dismay a phenomenon known as the "black drop." The visual appearance at ingress and egress makes it difficult to determine the EXACT moment when Venus touches the limb of the Sun.

Image taken from
Cook and Green, Philosophical Transactions of the Royal Society,
vol 61, p. 397 (1771)

Photographs can make the job easier, but even if you manage to collect a series of photographs like the one below (click on the image to animate), how precisely can you determine the position of the center or edges of the small black dot within a large bright circle?

Thanks to Sky and Telescope
for making the movie available
On the other hand, the asteroid Eros is so small, and so far from Earth even at its closest, that it appears in our ground-based telescopes to be a tiny little dot of light. Around it are many other tiny little dots of light: the stars.

Image courtesy of
Fernando Mejido
Astronomers have centuries of experience in measuring the positions of tiny little dots of light, so the position of Eros can be measured to a very high precision. For example, Trumpler et al. (1937) report that each of their measurements of Eros, made in 1931 using a camera mounted on a 5-inch refractor at Lick Observatory, have a typical uncertainty in position of only 0.11 arcsec. That's pretty good! Such precise positions can lead to very accurate values for the distance to Eros, and hence for the Astronomical Unit.
In the decades after the 1931 opposition of Eros, a few astronomers toiled to analyze the large number of measurements made around the world. They eventually figured out that, in order to fit all the observations properly, they would have to modify the masses of the Earth and Moon slightly, and account for perturbations by all the other planets, and deal with additional complications. But the results were VERY good.
|
You will, in just a few months, have a chance to re-enact one of the classic astronomical experiments. On June 5, 2012, Venus will once again pass in front of the Sun. It marks the second and final transit in this century -- the next one won't occur until 2117!
The conditions won't be ideal for those of us watching from Rochester. We'll see Venus enter the Sun's disk just two hours or so before sunset.
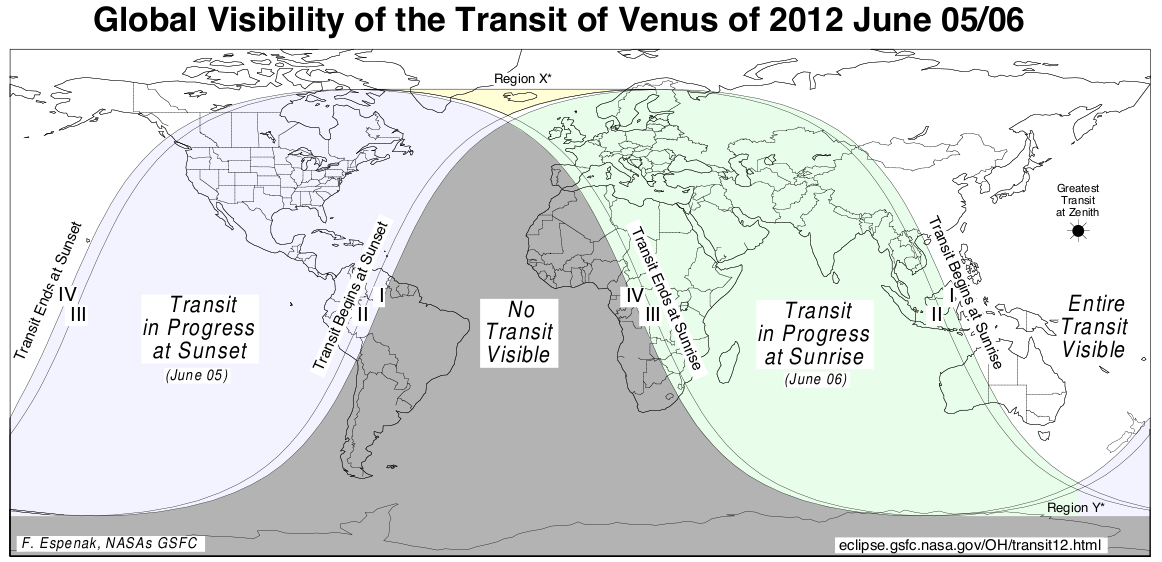
Map courtesy of
the NASA eclipse web site
If you'd like to participate in a global experiment, you can join in several ways.
 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.